2022-2-5动态规划day9

Posted 2022-02-05 阿ming

题1：

877. 石子游戏

Alice 和 Bob 用几堆石子在做游戏。一共有偶数堆石子，排成一行；每堆都有 正 整数颗石子，数目为 piles[i] 。

游戏以谁手中的石子最多来决出胜负。石子的 总数 是 奇数 ，所以没有平局。

Alice 和 Bob 轮流进行，Alice 先开始 。 每回合，玩家从行的 开始 或 结束 处取走整堆石头。 这种情况一直持续到没有更多的石子堆为止，此时手中 石子最多 的玩家 获胜 。

假设 Alice 和 Bob 都发挥出最佳水平，当 Alice 赢得比赛时返回 true ，当 Bob 赢得比赛时返回 false 。

 

示例 1：

输入：piles = [5,3,4,5]
输出：true
解释：
Alice 先开始，只能拿前 5 颗或后 5 颗石子 。
假设他取了前 5 颗，这一行就变成了 [3,4,5] 。
如果 Bob 拿走前 3 颗，那么剩下的是 [4,5]，Alice 拿走后 5 颗赢得 10 分。
如果 Bob 拿走后 5 颗，那么剩下的是 [3,4]，Alice 拿走后 4 颗赢得 9 分。
这表明，取前 5 颗石子对 Alice 来说是一个胜利的举动，所以返回 true 。

示例 2：

输入：piles = [3,7,2,3]
输出：true

 

提示：

• 2 <= piles.length <= 500
• piles.length 是 偶数
• 1 <= piles[i] <= 500
• sum(piles[i]) 是 奇数

 class Solution 
     public boolean stoneGame(int[] piles) 
         int n=piles.length;
         Result[][] dp=new Result[n][n];
         //区间dp
         //dp[i][j]表示i~j石堆的结果，fir是先手最大，sec是后手最大
         for (int i=0;i<n;i++)
             for (int j=i;j<n;j++)
                 dp[i][j]=new Result(0,0);
             
         
         //边界条件
         for (int i=0;i<n;i++) 
             dp[i][i].fir=piles[i];
             dp[i][i].sec=0;
         
         // 斜着 倒着遍历
         for (int i=n-2;i>=0;i--) 
             for (int j=i+1;j<n;j++) 
                 // 先手选择左边和右边的结果
                 int left=dp[i+1][j].sec+piles[i];
                 int right=dp[i][j-1].sec+piles[j];
                 if (left>right) 
                     dp[i][j].fir=left;
                     dp[i][j].sec=dp[i+1][j].fir;
                 else 
                     dp[i][j].fir=right;
                     dp[i][j].sec=dp[i][j-1].fir;
                 
             
         
         return dp[0][n-1].fir>dp[0][n-1].sec;
     
 
 
 class Result
     int fir;
     int sec;
     //fir表示先手
     //sec表示后手
     Result(int fir,int sec)
         this.fir=fir;
         this.sec=sec;
     
 

思路：通用动态规划思路如注释。

题2：

64. 最小路径和

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

 

示例 1：

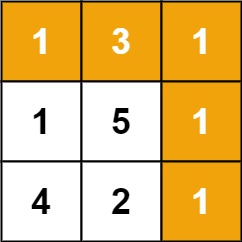
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

示例 2：

输入：grid = [[1,2,3],[4,5,6]]
输出：12

 

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 200
• 0 <= grid[i][j] <= 100

 class Solution 
     public int minPathSum(int[][] grid) 
         int m=grid.length,n=grid[0].length;
         int[][] dp=new int[m+1][n+1];
         for (int i=0;i<=m;i++) Arrays.fill(dp[i],Integer.MAX_VALUE);
         dp[0][1]=0;
         dp[1][0]=0;
         for (int i=1;i<=m;i++) 
             for (int j=1;j<=n;j++) 
                 dp[i][j]=Math.min(dp[i-1][j],dp[i][j-1])+grid[i-1][j-1];
             
         
         return dp[m][n];
     
 

思路：dp[i][j]表示到达i-1,j-1坐标的最小值。为了防止数组越界，多开一行一列数组。边界条件，要让dp[1][1] 为grid[0][0]， 让dp[1][0]或者dp[0][1]一个取0，其余初始值取最大值。