如何理解差分数组？

Posted 2022-01-25 7Aom1

差分数组

1、问题背景

如果给你一个包含5000万个元素的数组，然后会有频繁区间修改操作，那什么是频繁的区间修改操作呢？比如让第1个数到第1000万个数每个数都加上1，而且这种操作时频繁的。

此时你应该怎么做？很容易想到的是，从第1个数开始遍历，一直遍历到第1000万个数，然后每个数都加上1，如果这种操作很频繁的话，那这种暴力的方法在一些实时的系统中可能就拉跨了。

因此，今天的主角就出现了——差分数组。

2、算法原型

比如我们现在有一个数组arr , arr=0,2,5,4,9,7,10,0

那么差分数组是什么呢？其实差分数组本质上也是一个数组，我们暂且定义差分数组为d，差分数组d的大小和原来arr数组大小一样，而且di=arri-arri-1，且di=0，它的含义是什么？就是原来数组i位置上的元素和i-1位置上的元素作差，得到的值就是di的值。

所以，例子中的arr数组其对应的差分数组值如下图所示。

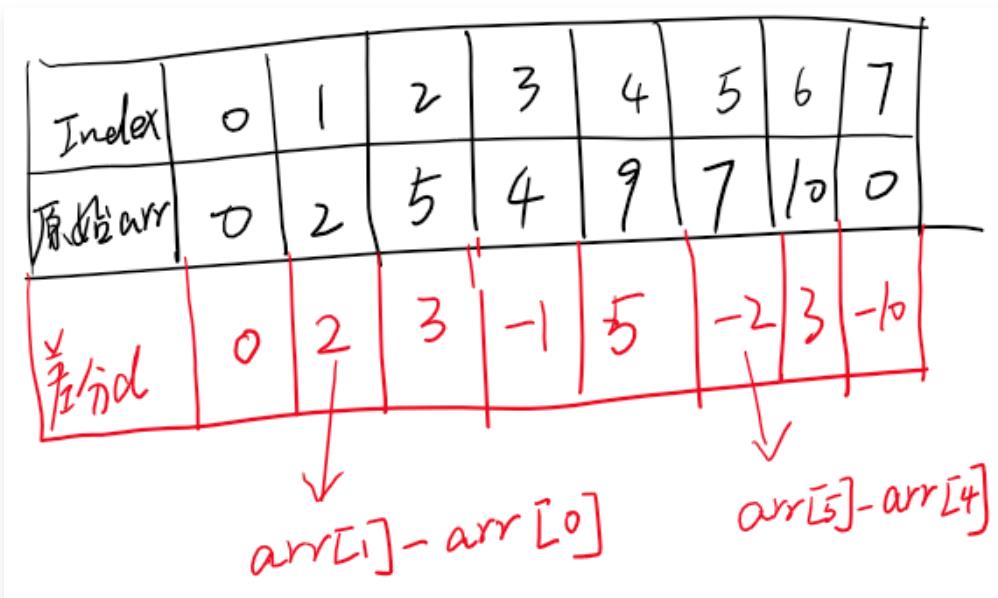
那么构造了这么个玩意有什么用呢？难道是来浪费宝贵的内存空间的？嗯，确实是来浪费宝贵的内存了，但是却换了时间上的高效。

现在我们有这么一个区间修改操作，即在区间1~4上，所有的数值都加上3

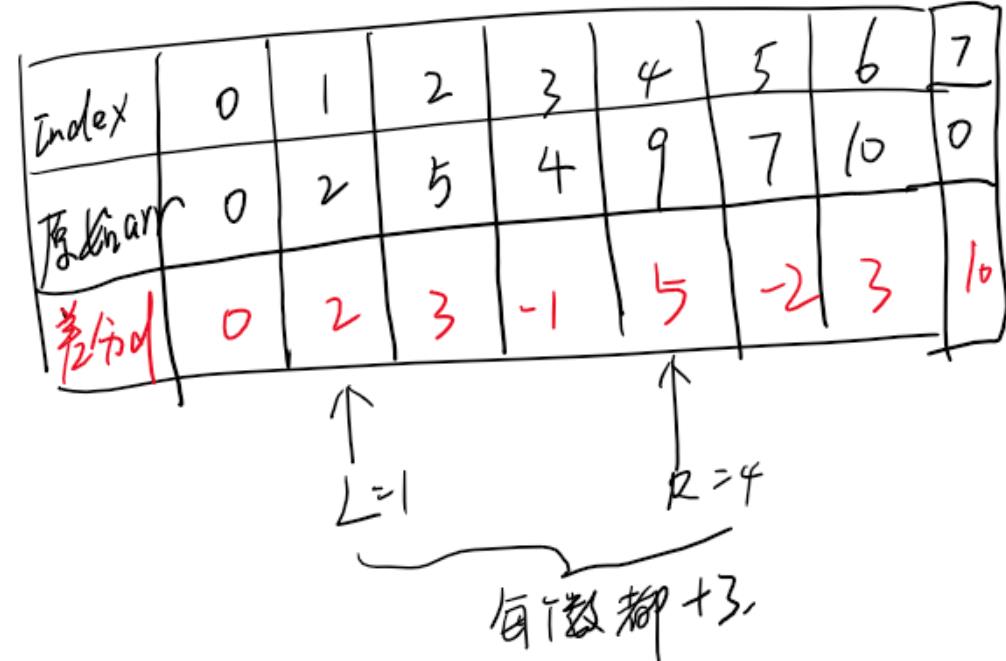
我们不要傻傻地遍历arr数组的1，4范围，然后再分别给每个值加上3，我们此时更改差分数组d即可。

显而易见，差分数组d在2，4范围内的值都不用改变，只需要改变差分数组位置1和位置5的值即可，即d1=d1+3，而d5=d5-3，其余不变，为什么呢？因为差分数组的定义——di=arri-arri-1

现在，我们如何根据差分数组d来推测arr中某一个位置的值呢？

比如，此时，我们想知道arr1的值，我们不能直接通过arr1得到原来的值，因为在区间修改的操作中我们并没有修改arr的值，因此我们必须从前往后遍历递推，由于d0=arr0-0(我们定义arr0的前一个数为0)，那么arr0=d0=0，又由于d1=arr1-arr0=5，那么arr1=5+arr0=5。以此类推，由于d2=arr2-arr1=3，所以arr2=3+arr1=8。

即对于每一个d[i]来说，它都有以下公式

d[i] = a[i+1] - a[i]

那么对应每个a[i]我们都可以推出与a[0]的关系

a[i] = d[0] + d[1] + ... + d[i-1] + a[0]

3、总结

可以看到，如果需要对L_{R范围内所有数都进行相同的操作，我们不需要从L}R遍历arr然后在每个值上进行相同操作，只需要在差分数组d中改变L和R+1的值即可。但是在查询arr数组中某个位置的数时，却要根据差分数组从前往后递推求值。

所以，该方法适用于区间频繁修改，而且这个区间范围是比较大的，离线查询的情况。