11.python排序算法之冒泡排序简单选择排序,二元选择排序直接插入排序
Posted videvops
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了11.python排序算法之冒泡排序简单选择排序,二元选择排序直接插入排序相关的知识,希望对你有一定的参考价值。
排序算法
冒泡排序Bubble Sort
- 交换排序
- 相邻元素两两比较大小,有必要则交换
- 元素越小或越大,就会在数列中慢慢的交换并“浮”向顶端,如同水泡咕嘟咕嘟往上冒
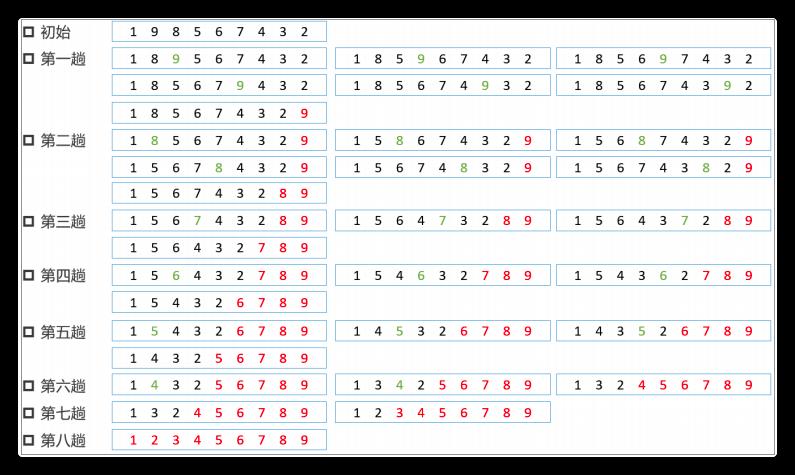
核心算法
- 排序算法,一般都实现为就地排序,输出为升序
- 扩大有序区,减小无序区。图中红色部分就是增大的有序区,反之就是减小的无序区
- 每一趟比较中,将无序区中所有元素依次两两比较,升序排序将大数调整到两数中的右侧
- 每一趟比较完成,都会把这一趟的最大数推倒当前无序区的最右侧
基本实现
思考时,将问题规模减小,一般2次不一定能找到规律,3次基本上可以看出规律。所以,我们思考时认为列表里面就只有4个元素。
nums = [1, 9, 8, 5] # 数字少好思考
print(nums)
length = len(nums) # 4
# 第一趟
i = 0
# 本趟内两两比较,大数换到右边
# 2个数比1下,3个数比2下,那么比较次数就是当前比较数个数-1
for j in range(length-1): # j 为0, 1, 2
print(j, nums[j], nums[j+1])
if nums[j] > nums[j+1]: # 只有大于才交换,小于等于就不用了
temp = nums[j]
nums[j] = nums[j+1]
nums[j+1] = temp
print(nums)
# i取0、1、2试一试
上面代码已经基本上完成了核心比较交换算法。下面解决每一趟的问题。
每一趟无序区是减小1个的,所以考虑使用两个循环,外面 i 循环表示趟,里面 j 循环表示每一趟的两两比较。内层 j 循环正好可以使用外层的 i,用在range(length-1-i),因为i第一次为0相当于没有减,第二次就是1了,这里range当计数器用表示走几趟。
i 循环控制趟数,4个数比较3趟就可以了。
nums = [1, 9, 8, 5] # 数字少好思考
#nums = [1, 9, 8, 5, 6, 7, 4, 3, 2]
print(nums)
length = len(nums) # 4
# i 控制趟数
for i in range(length-1):
# 本趟内两两比较,大数换到右边
# 2个数比1下,3个数比2下,那么比较次数就是当前比较数个数-1
for j in range(length-1-i): # j 为0, 1, 2
print(j, nums[j], nums[j+1])
if nums[j] > nums[j+1]: # 只有大于才交换,小于等于就不用了
temp = nums[j]
nums[j] = nums[j+1]
nums[j+1] = temp
print(nums)
print(\'result = \', nums)
可以增加两个变量:count表示比较的次数,count_swap表示交换的次数
nums = [1, 9, 8, 5] # 数字少好思考
#nums = [1, 9, 8, 5, 6, 7, 4, 3, 2]
print(nums)
length = len(nums) # 4
count = 0
count_swap = 0
# i 控制趟数
for i in range(length-1):
# 本趟内两两比较,大数换到右边
# 2个数比1下,3个数比2下,那么比较次数就是当前比较数个数-1
for j in range(length-1-i): # j 为0, 1, 2
count += 1
if nums[j] > nums[j+1]: # 只有大于才交换,小于等于就不用了
nums[j],nump[j+1] = nums[j+1],nump[j]
count_swap += 1
print(nums)
print(\'result = \', nums)
print(count, count_swap)
优化
思考:如果某一趟两两比较后没有发生任何交换,说明什么?
#nums = [1, 9, 8, 5] # 数字少好思考
#nums = [1, 9, 8, 5, 6, 7, 4, 3, 2]
nums = [9, 8, 1, 2, 3, 4, 5, 6, 7]
print(nums)
length = len(nums) # 4
count = 0
count_swap = 0
# 假设这一趟不需要交换了
finished = True # 定义标记
# i 控制趟数
for i in range(length-1):
# 本趟内两两比较,大数换到右边
# 2个数比1下,3个数比2下,那么比较次数就是当前比较数个数-1
for j in range(length-1-i): # j 为0, 1, 2
count += 1
if nums[j] > nums[j+1]: # 只有大于才交换,小于等于就不用了
temp = nums[j]
nums[j] = nums[j+1]
nums[j+1] = temp
count_swap += 1
finished = False # 有一次交换就要标记为False
if finished:
break
print(nums)
print(\'result = \', nums)
print(count, count_swap)
上面代码合适吗?
不合适。因为假设的是每一趟,只要有一趟没有发生交换,就可以认为已经是目标顺序了。要把标记放在 i 循环里。
if __name__ == \'__main__\':
count=0
count_swap=0
nums=[1,9,8,5]
for i in range(len(nums)-1):
finished=True
for j in range(len(nums)-1-i):
count+=1
if nums[j]>nums[j+1]:
nums[j],nums[j+1]=nums[j+1],nums[j]
count_swap+=1
finished=False
if finished:
break
print(nums,count,count_swap)
总结
- 冒泡法需要数据一趟趟比较
- 可以设定一个标记判断此轮是否有数据交换发生,如果没有发生交换,可以结束排序,如果发生交换,继续下一轮排序
- 最差的排序情况是,初始顺序与目标顺序完全相反,遍历次数1,...,n-1之和n(n-1)/2
- 最好的排序情况是,初始顺序与目标顺序完全相同,遍历次数n-1
- 时间复杂度O(n2)
简单选择排序
- 选择排序
- 每一趟两两比较大小,找出极值(极大值或极小值)并放置到有序区的位置
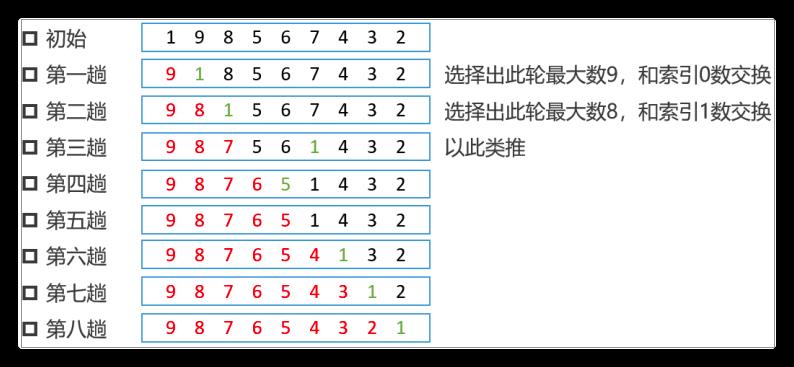
核心算法
- 结果可为升序或降序排列,默认升序排列。以降序为例
- 扩大有序区,减小无序区。图中红色部分就是增大的有序区,反之就是减小的无序区
- 相邻元素依次两两比较,获得每一次比较后的最大值,并记住此值的索引
- 每一趟都从无序区中选择出最大值,然后交换到当前无序区最左端
算法实现
if __name__ == \'__main__\':
count=0
count_swap=0
nums=[1,9,8,5,8,9,5,3,2,2,3,54,6,8,9,4,5]
for i in range(len(nums)-1):
count+=1
for j in range(len(nums)-1-i):
if nums[j]>nums[j+1]:
count_swap+=1
nums[j],nums[j+1]=nums[j+1],nums[j]
print(nums,count,count_swap)
二元选择排序
- 同时选择出每一趟的最大值和最小值,并分别固定到两端的有序区
- 减少迭代的趟数
m_list = [
[1, 9, 8, 5, 6, 7, 4, 3, 2],
[1, 2, 3, 4, 5, 6, 7, 8, 9],
[9, 8, 7, 6, 5, 4, 3, 2, 1] ]
nums = m_list[1]
length = len(nums)
print(nums)
count_iter = 0
count_swap = 0
for i in range(length//2): # 一次固定2个数,减半
maxindex = i # 正索引,假设无序区第一个就是最大数,其索引记作最大
minindex = -i-1 # 负索引,假设无序区最后一个就是最小数,其索引记作最小
for j in range(i+1, length-i): # 每次左边加一个,右边也要减一个,表示无序区两端
都减少
count_iter += 1
if nums[maxindex] < nums[j]:
maxindex = j
if nums[minindex] > nums[-j-1]:
minindex = -j -1
#print(maxindex, i, "|||", minindex, -i-1)
if maxindex != i:
nums[maxindex], nums[i] = nums[i], nums[maxindex]
count_swap += 1
# [1, 3, 2]为例,如果i位置上就是最小值,走到这里,说明最大值和最小值交换过了,要
调整最小值索引为maxindex
if i == length + minindex:
minindex = maxindex - length
if minindex != -i-1: # 负索引比较
nums[minindex], nums[-i-1]= nums[-i-1], nums[minindex]
count_swap += 1
print(nums)
print(count_iter, count_swap)
以上代码还有没有优化的可能?
如果一趟比较后,极大值、极小值的值相等,说明什么?
说明,剩余比较的数将全部相等,那么排序可以立即停止。
m_list = [
[1, 9, 8, 5, 6, 7, 4, 3, 2],
[1, 2, 3, 4, 5, 6, 7, 8, 9],
[9, 8, 7, 6, 5, 4, 3, 2, 1] ]
nums = m_list[1]
length = len(nums)
print(nums)
count_iter = 0
count_swap = 0
for i in range(length//2): # 一次固定2个数,减半
maxindex = i # 正索引,假设无序区第一个就是最大数,其索引记作最大
minindex = -i-1 # 负索引,假设无序区最后一个就是最小数,其索引记作最小
for j in range(i+1, length-i): # 每次左边加一个,右边也要减一个,表示无序区两端
都减少
count_iter += 1
if nums[maxindex] < nums[j]:
maxindex = j
if nums[minindex] > nums[-j-1]:
minindex = -j -1
#print(maxindex, i, "|||", minindex, -i-1)
if nums[maxindex] == nums[minindex]: # 元素全相同
break
if maxindex != i:
nums[maxindex], nums[i] = nums[i], nums[maxindex]
count_swap += 1
# [1, 3, 2]为例,如果i位置上就是最小值,走到这里,说明最大值和最小值交换过了,要
调整最小值索引为maxindex
if i == length + minindex:
minindex = maxindex - length
if minindex != -i-1: # 负索引比较
nums[minindex], nums[-i-1]= nums[-i-1], nums[minindex]
count_swap += 1
print(nums)
print(count_iter, count_swap)
考虑一种特殊情况
[1, 1, 1, 1, 1, 1, 1, 1, 2] 这种情况,找到的最小值索引是-2,最大值索引8,上面的代码会交换2次,最小值两个1交换是无用功,所以,增加一个判断
m_list = [
[1, 9, 8, 5, 6, 7, 4, 3, 2],
[1, 2, 3, 4, 5, 6, 7, 8, 9],
[9, 8, 7, 6, 5, 4, 3, 2, 1],
[1, 1, 1, 1, 1, 1, 1, 1, 1],
[1, 1, 1, 2] ]
nums = m_list[4]
length = len(nums)
print(nums)
count_iter = 0
count_swap = 0
for i in range(length//2): # 一次固定2个数,减半
maxindex = i # 正索引,假设无序区第一个就是最大数,其索引记作最大
minindex = -i-1 # 负索引,假设无序区最后一个就是最小数,其索引记作最小
for j in range(i+1, length-i): # 每次左边加一个,右边也要减一个,表示无序区两端
都减少
count_iter += 1
if nums[maxindex] < nums[j]:
maxindex = j
if nums[minindex] > nums[-j-1]:
minindex = -j -1
#print(maxindex, i, "|||", minindex, -i-1)
if nums[maxindex] == nums[minindex]: # 元素全相同
break
if maxindex != i:
nums[maxindex], nums[i] = nums[i], nums[maxindex]
count_swap += 1
# [1, 3, 2]为例,如果i位置上就是最小值,走到这里,说明最大值和最小值交换过了,要
调整最小值索引为maxindex
if i == length + minindex:
minindex = maxindex - length
if minindex != -i-1 and nums[minindex] != nums[-i-1]: # 负索引比较,值不一
样再交换
nums[minindex], nums[-i-1]= nums[-i-1], nums[minindex]
count_swap += 1
print(nums)
print(count_iter, count_swap)
总结
- 简单选择排序需要数据一趟趟比较,并在每一趟中发现极值
- 没有办法知道当前这一趟是否已经达到排序要求,但是可以知道极值是否在目标索引位置上
- 遍历次数1,...,n-1之和n(n-1)/2
- 时间复杂度O(n2)
- 减少了交换次数,提高了效率,性能略好于冒泡法
直接插入排序
- 插入排序
- 每一趟都要把待排序数放到有序区中合适的插入位置
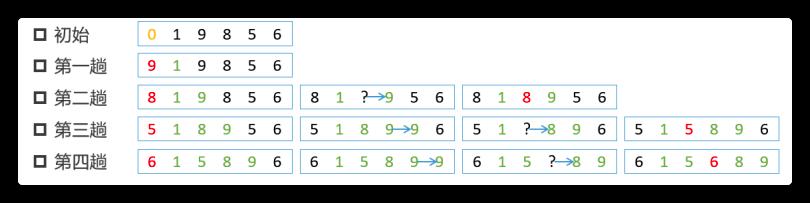
核心算法
- 结果可为升序或降序排列,默认升序排列。以升序为例
- 扩大有序区,减小无序区。图中绿色部分就是增大的有序区,黑色部分就是减小的无序区
- 增加一个哨兵位,图中最左端红色数字,其中放置每一趟待比较数值
- 将哨兵位数值与有序区数值从右到左依次比较,找到哨兵位数值合适的插入点
算法实现
- 增加哨兵位
- 为了方便,采用列表头部索引0位置插入哨兵位
- 每一次从有序区最右端后的下一个数,即无序区最左端的数放到哨兵位
- 比较与挪动
- 从有序区最右端开始,从右至左依次与哨兵比较
- 比较数比哨兵大,则右移一下,换下一个左边的比较数
- 直到找到不大于哨兵的比较数,这是把哨兵插入到这个数右侧的空位即可
m_list = [
[1, 9, 8, 5, 6, 7, 4, 3, 2],
[1, 2, 3, 4, 5, 6, 7, 8, 9],
[9, 8, 7, 6, 5, 4, 3, 2, 1] ]
nums = [0] + m_list[0]
print(nums[1:])
length = len(nums)
count_move = 0
for i in range(2, length): # 测试的值从nums的索引2开始向后直到最后一个元素
nums[0] = nums[i] # 索引0位哨兵,索引1位假设的有序区,都跳过
j = i - 1 # i左边的那个数就是有序区末尾
if nums[j] > nums[0]: # 如果最右侧数大于哨兵才需要挪动和插入
while nums[j] > nums[0]:
nums[j+1] = nums[j] # 右移,不是交换
j -= 1 # 继续向左
count_move += 1
nums[j+1] = nums[0] # 循环中多减了一次j
print(nums[1:])
总结
- 最好情况,正好是升序排列,比较迭代n-1次
- 最差情况,正好是降序排列,比较迭代1,2,...,n-1即 n(n-1)/2,数据移动非常多
- 使用两层嵌套循环,时间复杂度O(n^2)
- 稳定排序算法
- 如果待排序序列R中两元素相等,即Ri等于Rj,且i < j ,那么排序后这个先后顺序不变,这种排序算法就称为稳定排序
- 已经学习过的排序算法哪些是稳定排序,考虑1、1、2排序
- 使用在小规模数据比较
- 优化
- 如果比较操作耗时大的话,可以采用二分查找来提高效率,即二分查找插入排序
排序稳定性
- 冒泡排序,相同数据不交换,稳定
- 直接选择排序,相同数据前面的先选择到,排到有序区,不稳定
- 直接插入排序,相同数据不移动,相对位置不变,稳定
-------------------------------------------
个性签名:独学而无友,则孤陋而寡闻。做一个灵魂有趣的人!
如果觉得这篇文章对你有小小的帮助的话,记得在右下角点个“推荐”哦,博主在此感谢!
万水千山总是情,打赏一分行不行,所以如果你心情还比较高兴,也是可以扫码打赏博主,哈哈哈(っ•̀ω•́)っ✎⁾⁾!
以上是关于11.python排序算法之冒泡排序简单选择排序,二元选择排序直接插入排序的主要内容,如果未能解决你的问题,请参考以下文章