排序算法总结 go实现代码
Posted 布羽
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了排序算法总结 go实现代码相关的知识,希望对你有一定的参考价值。
排序算法的分类如下

各个算法的时间和空间代价如下
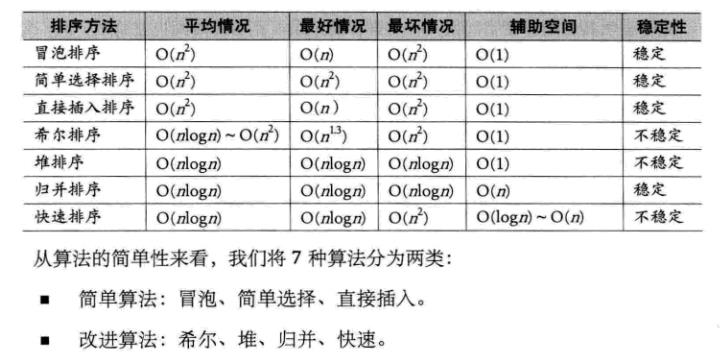
注:另外还有一个时间代价为O(N)的桶排序算法,局限性比较大,感兴趣可以另作了解。
那么,如何选择各个排序算法呢?
1. 首先,在待排序数组长度比较短的情况下,使用简单排序算法效果比较好。
在简单排序算法中,直接插入排序的平均情况是相对较好的。而简单选择排序则适合记录(数据元素)的关键字比较大的情况,因为选择排序的移动次数比较少,主要消耗在比较。
2. 如果数组长度比较长,需要考虑改进算法。
3.希尔排序的平均和最坏情况不如其他改进算法,不用重点考虑。
4.如果对稳定性有要求,考虑归并排序。
5.如果对辅助空间有限制,考虑堆排序
6.如果没有以上考虑,综合现实使用情况来看,快排算法,如其名,是使用最广泛,效果最好的,选它没错。
以下放go代码实现
package main import ( "fmt" ) //BSort0 最简单排序, func BSort0(nums []int) for i := 0; i < len(nums); i++ for j := i + 1; j < len(nums); j++ if nums[i] > nums[j] nums[i], nums[j] = nums[j], nums[i] //BSort1 冒泡排序 func BSort1(nums []int) for i := 0; i < len(nums)-1; i++ for j := len(nums) - 1; j > i; j-- if nums[j] < nums[j-1] nums[j], nums[j-1] = nums[j-1], nums[j] //BSort2 优化冒泡,增加了标志变量,如果一次J的循环下来发现没有产生交换,则直接return func BSort2(nums []int) flag := true for i := 0; i < len(nums)-1 && flag; i++ flag = false for j := len(nums) - 1; j > i; j-- if nums[j] < nums[j-1] nums[j], nums[j-1] = nums[j-1], nums[j] flag = true //SelectSort 简单选择排序,类似BSort0的思路,但是保存索引位,以减小交换次数 func SelectSort(nums []int) var minIndex int for i := 0; i < len(nums); i++ minIndex = i for j := i + 1; j < len(nums); j++ if nums[minIndex] > nums[j] minIndex = j nums[i], nums[minIndex] = nums[minIndex], nums[i] //InsertSort 插入排序,参考整理扑克 func InsertSort(nums []int) var i, j, temp int for i = 1; i < len(nums); i++ temp = nums[i] for j = i; j > 0; j-- if temp < nums[j-1] nums[j] = nums[j-1] else break nums[j] = temp //ShellSort 思路就是将一个长序列,按照h为间隔拆分成多个子序列(交叉拆分),对每个子序列插入排序。不断减小h,重复上述行为。最后h=1再执行一次插入排序。 func ShellSort(nums []int) var i, j, temp int n := len(nums) h := n/3 + 1 for h >= 1 //i从h开始,因为每个子序列的第一个元素默认排好了 for i = h; i < n; i++ temp = nums[i] for j = i; j > h-1; j -= h if temp < nums[j-h] nums[j] = nums[j-h] else break nums[j] = temp h /= 3 //HeapAdjust堆调整函数,默认(s,m]区间内的元素已经满足大顶堆性质,调整nums[s] func HeapAdjust(nums []int, s int, m int) temp := nums[s] for i := 2 * s; i <= m; i *= 2 if i < m && nums[i] < nums[i+1] i++ if nums[i] < temp break else nums[s] = nums[i] s = i nums[s] = temp //HeapSort 堆排序,将一个堆按层次序编号,编号就是数组索引,将这个堆放在数组中,每次抽走根节点(最小或者最大),剩下的堆从新调整,维持最小顶或者最大顶性质。 //实现最大顶堆排序算法,堆排序比较特殊,数组索引应该从1开始,而不是0。 func HeapSort(nums []int) n := len(nums) - 1 //初始化,从最底层的非叶节点开始,往上调整 for i := n / 2; i >= 1; i-- HeapAdjust(nums, i, n) //开始排序 for i := 0; i < n-1; i++ nums[1], nums[n-i] = nums[n-i], nums[1] HeapAdjust(nums, 1, n-i-1) //归并排序,有递归版本和迭代版本,这里直接实现迭代版本 //Merge 合并[a,b]和[b+1,c] func Merge(SR []int, TR []int, a int, b int, c int) i, s := a, a j := b + 1 for ; i <= b && j <= c; s++ if SR[i] < SR[j] TR[s] = SR[i] i++ else TR[s] = SR[j] j++ if i <= b for ; i <= b; i++ TR[s] = SR[i] s++ if j <= c for ; j <= c; j++ TR[s] = SR[j] s++ //MergePass 归并SR中长度为s的子序列,n为序列总长度 func MergePass(SR []int, TR []int, s int, n int) var i int for i = 0; i < n-2*s; i += 2 * s Merge(SR, TR, i, i+s-1, i+2*s-1) //如果剩余长度大于s,那么合并两个子序列(其中一个长度为s) if n-i+1 > s Merge(SR, TR, i, i+s-1, n-1) else for j := i; j < n; j++ TR[j] = SR[j] //MergeSort 归并排序,有递归版本和迭代版本,这里直接实现迭代版本 func MergeSort(nums []int) TR := make([]int, len(nums)) k := 1 for k < len(nums) MergePass(nums, TR, k, len(nums)) k *= 2 if k >= len(nums) nums = TR break else MergePass(TR, nums, k, len(nums)) k *= 2 //Partition 取nums[low]为中枢值,将[low,high]之间的数分割到左右两边 func Partition(nums []int, low int, high int) int temp := nums[low] for low < high //先搜索右边 for low < high && temp < nums[high] high-- nums[low], nums[high] = nums[high], nums[low] for low < high && temp > nums[low] low++ nums[low], nums[high] = nums[high], nums[low] return low //Partition2 优化不必要的交换,取nums[low]为中枢值,将[low,high]之间的数分割到左右两边 func Partition2(nums []int, low int, high int) int temp := nums[low] for low < high for low < high && nums[high] > temp high-- nums[low] = nums[high] for low < high && nums[low] < temp low++ nums[high] = nums[low] nums[low] = temp return low //QSort 递归快排函数,对[a,b]之间的区域快排 func QSort(nums []int, a int, b int) if a < b q := Partition(nums, a, b) QSort(nums, a, q-1) QSort(nums, q+1, b) //QSort2 尾递归优化版本,基于尾递归的思想,将尾递归转变为迭代,减少初始序列极度不平衡下的函数栈的深度。这种优化主要是为了减小栈空间的利用和切换的时间代价。 func QSort2(nums []int, a int, b int) for a < b q := Partition(nums, a, b) QSort2(nums, a, q-1) a = q + 1 //QuickSort 快排入口 func QuickSort(nums []int) QSort2(nums, 0, len(nums)-1) //其它的快排优化:
//1.根据数组大小,小于某个阈值时,使用直接插入排序,否则使用快排
//2. 优化选取中枢值,根据数组的大小,随机选择一定数量的数据元,进行排序,选出中间的值作为中枢值
func main() tt := []int5, 6, 9, 4, 7, 3, 1, 8, 2 //tt := []int2, 1, 3, 4, 5, 6, 7 QuickSort(tt) fmt.Println(tt)
以上是关于排序算法总结 go实现代码的主要内容,如果未能解决你的问题,请参考以下文章