各种排序整理详解

Posted 2021-12-03 yemanlin

diary

11.04
1.马上就要期中考了,现在什么也没复习,慌成dog
2.从语文老师口中知道,班主任一直很关心我的学科成绩(特别是Chinese,非常感动_(≧▽≦)/啦啦啦)

11.16
1.换了新同桌，卡星
2.跟新同桌说奖励他一个大笔豆子，他欣然答应，最后一下“啪”的清脆和红红的脸，就不必我多说了
3.跟同学讨论—— ——在人死之前打了别人一下是不是血赚

11.23
1.自认为自己的性格不太好，喜欢讲话，之后要改
2.遇到一个豪华绿钻的QQ音乐用户，就用他/她的账号把自己的歌单下完了

11.28
1.最近发现了一个新game,哎了哎了

让我们进入今天的正题

目录

• \\(冒泡排序（Bubble Sort）\\)
• \\(插入排序（Insertion Sort）\\)
• \\(希尔排序（Shell Sort）\\)
• \\(选择排序（Selection Sort）\\)
• \\(快速排序（Quick Sort）\\)
• \\(归并排序（Merge Sort）\\)
• \\(堆排序（Heap Sort）\\)
• \\(计数排序（Counting Sort）\\)
• \\(桶排序（Bucket Sort）\\)
• \\(基数排序（Radix Sort）\\)

一.冒泡排序

冒泡排序是一种交换排序，核心是冒泡，把数组中最小的那个往上冒，冒的过程就是和他相邻的元素交换。

重复走访要排序的数列，通过两两比较相邻记录的排序码。
比较相邻的元素。如果第一个比第二个大，就交换他们两个。

对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。

持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

性能分析

稳定性：稳定
平均时间复杂度：\\(O(N^2)\\)
最佳时间复杂度：\\(O(N)\\)
最差时间复杂度：\\(O(N^2)\\)

模拟过程

二.插入排序

插入排序操作类似于摸牌并将其从大到小排列。每次摸到一张牌后，根据其点数插入到确切位置。

① 从第一个元素开始，该元素可以认为已经被排序
② 取出下一个元素，在已经排序的元素序列中从后向前扫描
③如果该元素（已排序）大于新元素，将该元素移到下一位置
④ 重复步骤③，直到找到已排序的元素小于或者等于新元素的位置
⑤将新元素插入到该位置后
⑥ 重复步骤②~⑤

性能分析

稳定性：稳定
最差时间复杂度：\\(O(N^2)\\)
平均时间复杂度：\\(O(N^2)\\)

模拟过程

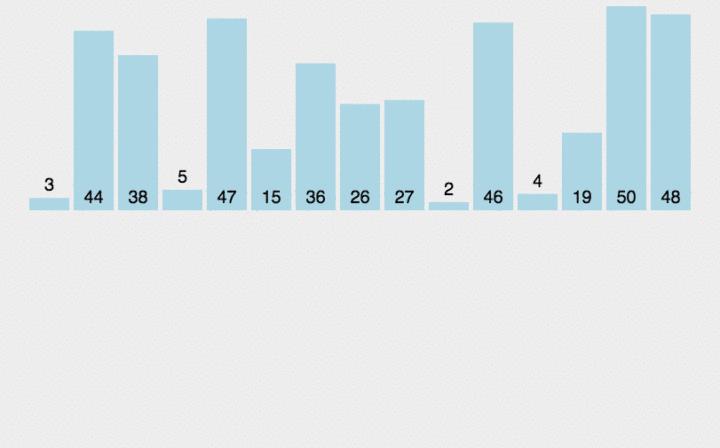
三.希尔排序

希尔排序的实质就是分组插入排序，该方法又称递减增量排序算法，因Donald Shell(希尔)于1959年提出而得名。希尔排序是非稳定的排序算法。

① 先取一个小于n的整数d1作为第一个增量，把文件的全部记录分成d1个组。
② 所有距离为d1的倍数的记录放在同一个组中，在各组内进行直接插入排序。
③ 取第二个增量d2小于d1重复上述的分组和排序，直至所取的增量dt=1(dt小于dt-l小于…小于d2小于d1)，即所有记录放在同一组中进行直接插入排序为止。

性能分析

稳定性：不稳定
最差时间复杂度：\\(O(N^2)\\)
平均时间复杂度：\\(O(Nlog_2N)\\)

模拟过程

假设有一组｛9, 1, 2, 5, 7, 4, 8, 6, 3, 5｝无需序列。

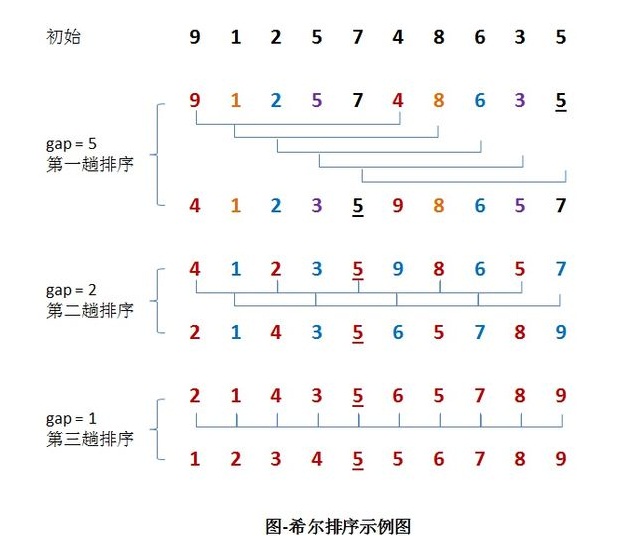
第一趟排序： 设 gap1 = N / 2 = 5，即相隔距离为 5 的元素组成一组，可以分为 5 组。接下来，按照直接插入排序的方法对每个组进行排序。
第二趟排序：
将上次的 gap 缩小一半，即 gap2 = gap1 / 2 = 2 (取整数)。这样每相隔距离为 2 的元素组成一组，可以分为2组。按照直接插入排序的方法对每个组进行排序。
第三趟排序：
再次把 gap 缩小一半，即gap3 = gap2 / 2 = 1。 这样相隔距离为1的元素组成一组，即只有一组。按照直接插入排序的方法对每个组进行排序。此时，排序已经结束。

四.选择排序

首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

选择排序的思想其实和冒泡排序有点类似，都是在一次排序后把最小的元素放到最前面，或者将最大值放在最后面。但是过程不同，冒泡排序是通过相邻的比较和交换。而选择排序是通过对整体的选择，每一趟从前往后查找出无序区最小值，将最小值交换至无序区最前面的位置。

① 第一轮从下标为 1 到下标为 n-1 的元素中选取最小值，若小于第一个数，则交换
② 第二轮从下标为 2 到下标为 n-1 的元素中选取最小值，若小于第二个数，则交换
③ 依次类推下去……

性能分析

稳定性：不稳定
平均时间复杂度：O(N^2)
最佳时间复杂度：O(N^2)
最差时间复杂度：O(N^2)

模拟过程

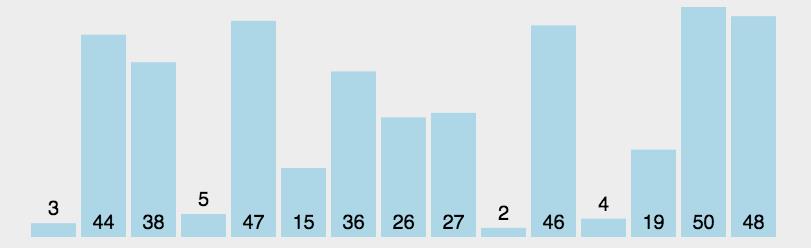
五.快速排序

有二分思想

• 选择A中的任意一个元素pivot（选哪个点都行，推荐选中间因为舒服，但个人喜欢坐着选），该元素作为基准
• 将小于基准的元素移到左边，大于基准的元素移到右边（分区操作）
• A被pivot分为两部分L 和 R，继续对L和R做同样的处理
• 直到所有子集元素不再需要进行上述步骤

性能分析

稳定性：不稳定
平均时间复杂度：O(NlogN)
最佳时间复杂度：O(NlogN)
最差时间复杂度：O(N^2)

模拟过程

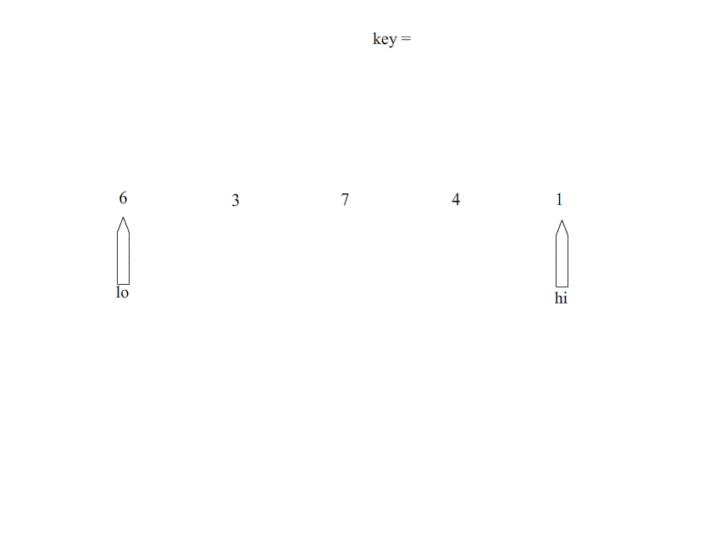
六.归并排序

归并排序是用分治思想，分治模式在每一层递归上有三个步骤：

• 分解（Divide）：将n个元素分成个含n/2个元素的子序列。
• 解决（Conquer）：用合并排序法对两个子序列递归的排序。
• 合并（Combine）：合并两个已排序的子序列已得到排序结果。

1.递归分解，将数组分解成left和right。如果这两个数组内部数据是无序的，则对数组进行二分，直至分解出的小组只有一个元素，此时认为该小组内部有序。
2.合并两个有序数组，比较两个数组的最前面的数，谁小就先取谁，该数组的指针往后移一位。
3.重复步骤2，直至一个数组为空。
4.最后把另一个数组的剩余部分复制过来即可。

性能分析

稳定性：稳定
平均时间复杂度：O(NlogN)
最佳时间复杂度：O(N)
最差时间复杂度：O(NlogN)

模拟过程

七.堆排序

虽然STL大法好,但是还是要写一下的(兢兢业业的博主不多了)
1.将数据存起来建一个大根堆
2.将堆顶与末尾交换,并输出(相当于不要了),再用剩下的点建一个大根堆
3.直至变成小根堆为止

性能分析

稳定性：不稳定
平均时间复杂度：O(nlogn)
最佳时间复杂度：O(nlogn)
最差时间复杂度：O(nlogn)

Why not 模拟过程?

because it is too easy to see(mainly is that I can\'t insert mp4)

But I can give a website
模拟过程

八.计数排序

计数排序（Counting sort）是一种稳定的线性时间排序算法。

注意:不是桶排序

① 分配。扫描一遍原始数组，以数值作为下标，将该下标的计数器增1。
② 收集。扫描一遍计数器数组，按顺序把值收集起来。

性能分析

稳定性：稳定
平均时间复杂度：O(n + k)
最佳时间复杂度：O(n + k)
最差时间复杂度：O(n + k)
空间复杂度：O(n + k)

模拟过程

九.桶排序

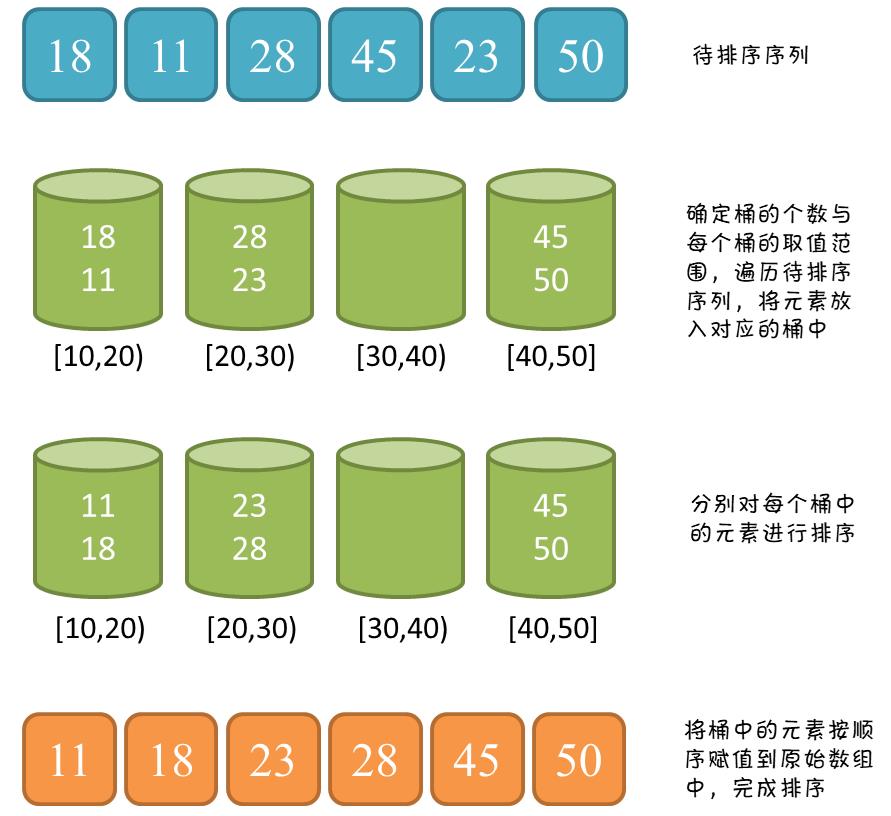
一句话总结：划分多个范围相同的区间，每个子区间自排序，最后合并。

桶排序是计数排序的扩展版本，计数排序可以看成每个桶只存储相同元素，而桶排序每个桶存储一定范围的元素，通过映射函数，将待排序数组中的元素映射到各个对应的桶中，对每个桶中的元素进行排序，最后将非空桶中的元素逐个放入原序列中。

桶排序需要尽量保证元素分散均匀，否则当所有数据集中在同一个桶中时，桶排序失效。

性能分析

稳定性：稳定
平均时间复杂度：O(n + k)
最佳时间复杂度：O(n + k)
最差时间复杂度：O(n ^ 2)
空间复杂度：O(n * k)

模拟无过程,只有图(嘻!)

十.基数排序

基数排序\\((Radix Sort)\\)是桶排序的扩展，它的基本思想是：将整数按位数切割成不同的数字，然后按每个位数分别比较。

具体做法是：将所有待比较数值统一为同样的数位长度，数位较短的数前面补零。然后，从最低位开始，依次进行一次排序。这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列。

性能分析

稳定性：稳定
时间复杂度：O(k*N)
空间复杂度：O(k + N)

模拟过程

Last(结束)

总共十个排序,制作不易,跪求点个赞,谢谢!