动态规划---例题4.最大子矩阵和问题
Posted PGokc
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了动态规划---例题4.最大子矩阵和问题相关的知识，希望对你有一定的参考价值。
本题与力扣面试题 17.24. 最大子矩阵相同.
一.问题描述
给定一个正整数、负整数和 0 组成的 N × M 矩阵，编写代码找出元素总和最大的子矩阵。
返回一个数组 [r1, c1, r2, c2]，其中 r1, c1 分别代表子矩阵左上角的行号和列号，r2, c2 分别代表右下角的行号和列号。若有多个满足条件的子矩阵，返回任意一个均可。
二.解题思路
如果有看过经典例题3 --- 最大子段和,就会很快知道该问题的突破口.
我们知道,最大子段和是针对一维数组而言,可以找到该数组中连续子数组之和最大的那一个.而对于本题,我们需要求解最大子矩阵和,就是将一维问题转化为了二维问题.最大子矩阵和问题是最大子段和问题向二维的推广.
我们用a[1:m] [1:n]表示给定的m行n列的整数矩阵.子数组a[i1:i2] [j1:j2]表示左上角和右下角行列坐标分别为(r1, c1)和(r2, c2)的子矩阵,
其各元素之和记为:
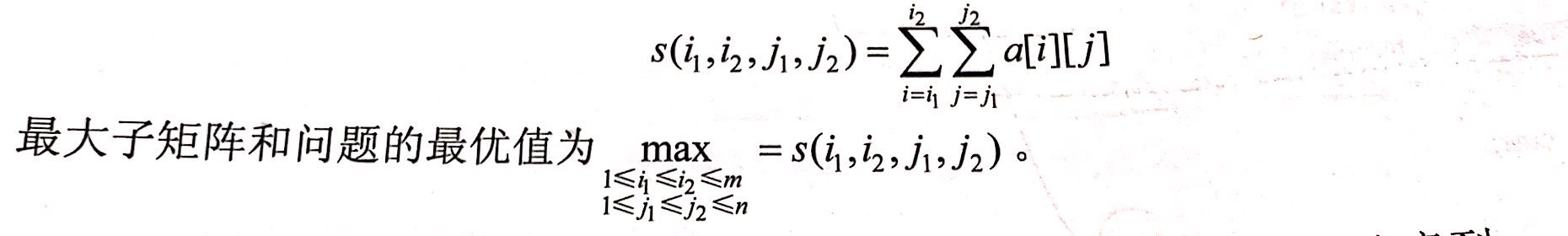
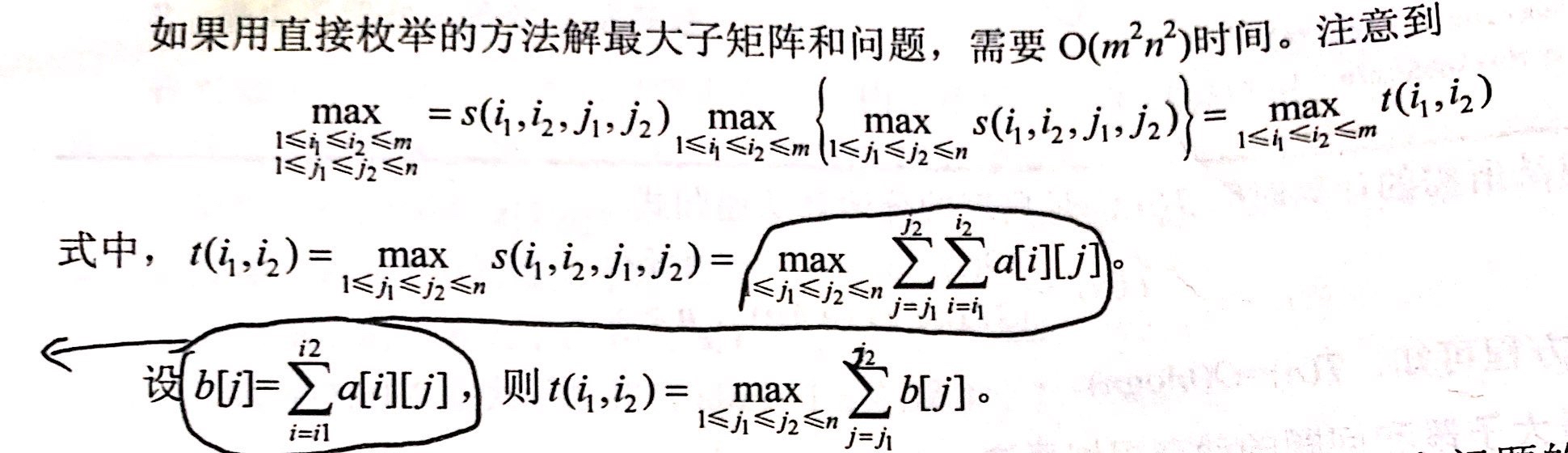
容易看出(不太容易
以上是关于动态规划---例题4.最大子矩阵和问题的主要内容，如果未能解决你的问题，请参考以下文章
算法211动态规划的引入 ——最大子矩阵（来自北京大学POJ）
最大子矩阵，最大连续子数组进阶，动态规划初级，poj1050