动态规划---例题7.图像压缩

Posted 2021-12-03 PGokc

一.题目描述

数字化图像是n*n的像素阵列. 假定每个像素有一个0~255的灰度值, 因此存储一个像素至多需8位.
为了减少存储空间, 采用变长模式, 即不同像素用不同位数来存储, 步骤如下:

• 图像线性化:将nn维图像转换为1n2向量 {p1,p2,...pn^2}
• 分段: 将像素分成连续的m段s1,s2,...sm,使每段中的像素存储位数相同. 每个段是相邻像素的集合且每段最多含256个像素, 若相同位数的像素超过 256个的话, 则用两个以上段表示。
• 创建三个表
  l: l[i]存放第i段长度, 表中各项均为8位长
  B: b[i]存放第i段中像素的存储位数,表中各项均为3位长.
  P: {p1,...p n2}以变长格式存储的像素的二进制串。

设产生了m个段,则存储第i段像素所需要的空间为 : **l[i] * b[i] + 11 **
(l[i] * b[i]表示这一段像素本身需要的信息, 11则表示这一段的长度l[i]以及该段像素每一个都用几位来表示b[i], 即3 + 8 = 11位)
总存储空间为 11m+∑ l[i]*b[i] ；
问题要求找到一个最优分段。使存储空间最少.

例题:
考察4*4图像

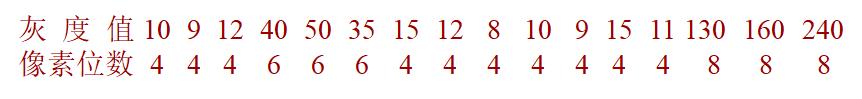
让我们一步一步地来优化:
①不分段,不采用变长压缩.
灰度值序列P:
00001010 00001001 00001100 00111000 00110010 00100011...
易得总存储空间为:
16 * 8 = 128位

②分段: [10, 9, 12], [40, 50, 35], [15, 12, 8, 10, 9, 15, 11], [130, 160, 240]
L={3，3， 7，3}；B={4，6，4，8}；
P包含16个灰度值，其中头三个各用4位存储，接下来三个各用6位再接下来的七个各用4位，最后三个各用8位存储。
1010 1001 1100 111000 110010 100011 ...

三个表需要存储空间分别为:
L: 32位 (4 * 8)
B: 12位 (3 * 4)
P: 82位 (4 * 3 + 6 * 3 + 4 * 7 + 8 * 3)
总存储空间:32 + 12 +82 = 126位

③若我们将段1,段2合并,则相应地三个表更新为:
L={6, 7, 3}; B={6, 4, 8};
P: 001010 001001 001100 111000 110010 100011...
其余不变.
三个表的存储空间变为:
L: 24位(3 * 8)
B: 9位(3 * 3)
P: 88位(6 * 6 + 4 * 7 + 8 * 3)
总存储空间:24 + 9 + 88 = 121位(减少了5位)

故图像压缩问题就是要我们找出一个最优的分段方案,使得总存储空间最小.

二.解题思路

算法思路 :化为多步决策, 先求有一个段时的最优分段,再求有2个段时的最优分段,有3个段时的最优分段...

1.最优解结构 :

设n个段的最优合并为C, 若在合并C中,第n段与n-1,n-2,...n-k+1段合并, 则n-1,n-2,...n-k+1段的合并也必是最优的.
最优合并C所需要的空间消耗为:
第一段到第n-k段最优合并空间 + Lsum(n-k+1,n) * Bmax(n-k+1,n)+11
其中 Lsum(a, b) = 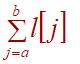, Bmax(a, b) = max{ B[a],..., B[b] }

2.递归计算最优值

令s[i]为前i个段最优合并的存储位数,则:
s[i] =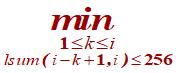
{s[i-k]+ lsum(i-k+1,i)*bmax(i-k+1,i) } +11

3.构造最优解

构造最优解: 记k[i]为s[i]取得最小值时k的值, 可由k的值构造相应的最优解.
算法Compress用l[i]和b[i]分别记录了最有分段所需的信息.最有分段的最后一段的段长度和像素位数分别存储于l[n], b[n]中,前一段的段长度和像素位数存储于l[n - l[n]]和 b[n - l[n]]中.
以此类推,由算法计算出的l和b可在O(n)时间内构造出相应的最优解.

具体代码如下:

// 图像压缩
#include<bits/stdc++.h>
using namespace std;
int length(int i)  //计算像素点p所需要的存储位数
{
    int k = 1;
    i = i/2;
    while(i>0)
    {
        k++;
        i = i/2;
    }
    return k;
}
void Compress(int n, int p[], int s[], int l[], int b[])  //令s[i]为前i个段最优合并的存储位数
{ 
    int Lmax = 256, header = 11;
    s[0] = 0;
    for(int i=1; i<=n; i++)  //i表示前几段
    {
        b[i] = length(p[i]); //计算像素点p需要的存储位数
        int bmax = b[i];
        cout<<i<<"bmax: "<<bmax<<endl;
        s[i] = s[i-1] + bmax;  //故下面j从2开始  
        l[i] = 1;
        for(int j=2; j<=i && j<=Lmax; j++)   //递推关系:s[i]=  min(1<=j<=i)(lsum(i-j+1, i)<=256) {s[i-j]+ lsum(i-j+1,i)*bmax(i-j+1,i) } + 11
        {
            if(bmax < b[i-j+1])
                bmax = b[i-j+1];
            if(s[i] > s[i-j] + j*bmax)   //因为一开始所有序列并没有分段,所以可以看作每一段就是一个数,故lsum(i-j+1, i) = j;
            {
                s[i] = s[i-j] + j*bmax;
                l[i] = j;   //最优断开位置,l[i]表示前i段的最优分段方案中应该是在i-j处断开  比如l[5] = 3,这表示前五段的最优分段应该是(5-3=2)处断开,s[5] = s[2] + 3*bmax   
                            //即 12 | 345,以此类推,得到l[n];之后构造最优解时再由l[n]向前回溯
            }
        }
        s[i] += header;
    }
}
void Traceback(int n, int &m, int s[], int l[])
{
    if(n == 0) return;
    Traceback(n-l[n], m, s, l);
    s[m++] = n-l[n];  //重新为s[]数组赋值，用来存储分段位置
}
void Output(int s[], int l[], int b[], int n)
{
    cout<<"The optimal value is "<<s[n]<<endl;
    int m = 0;
    Traceback(n, m, s, l);
    s[m] = n;
    cout<<"Decompose into "<<m<<" segments "<<endl;
    for(int j=1; j<=m; j++)
    {
        l[j] = l[s[j]];
        b[j] = b[s[j]];
    }
    for(int j=1; j<=m; j++)
        cout<<"段长度:"<<l[j]<<" 所需存储位数:"<<b[j]<<endl;
}
int main()
{
    int n;
    while(cin>>n && n)
    {
        int p[n+1];
        int s[n+1], l[n+1], b[n+1];
        for(int i=1; i<=n; i++)
            cin>>p[i];
        Compress(n, p, s, l, b);
        int m=0;
        Traceback(n, m, s, l);
        Output(s, l, b, n);
        memset(p, sizeof(p), 0);
    }
    system("pause");
    return 0;
}

运行结果:

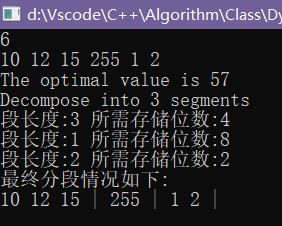
本篇文章参考我的老师毕方明《算法设计与分析》课件.
欢迎大家访问我的个人博客 --- 乔治的编程小屋,和我一起为大厂offer努力吧!