经典排序算法及python实现

Posted 情难眠2

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了经典排序算法及python实现相关的知识，希望对你有一定的参考价值。

今天我们来谈谈几种经典排序算法，然后用python来实现，最后通过数据来比较几个算法时间

选择排序

选择排序（Selection sort）是一种简单直观的排序算法。它的工作原理是每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。 选择排序是不稳定的排序方法（比如序列[5， 5， 3]第一次就将第一个[5]与[3]交换，导致第一个5挪动到第二个5后面）。（注：选自百度百科）

假如，有一个无须序列A={6,3,1,9,2,5,8,7,4}，选择排序的过程应该如下：
   第一趟：选择最小的元素，然后将其放置在数组的第一个位置A[0]，将A[0]=6和A[2]=1进行交换，此时A={1,3,6,9,2,5,8,7,4}；
   第二趟：由于A[0]位置上已经是最小的元素了，所以这次从A[1]开始，在剩下的序列里再选择一个最小的元素将其与A[1]进行交换。即这趟选择过程找到了最小元素A[4]=2，然后与A[1]=3进行交换，此时A={1,2,6,9,3,5,8,7,4}；
   第三趟：由于A[0]、A[1]已经有序，所以在A[2]~A[8]里再选择一个最小元素与A[2]进行交换，然后将这个过程一直循环下去直到A里所有的元素都排好序为止。这就是选择排序的精髓。因此，我们很容易写出选择排序的核心代码部分，即选择的过程，就是不断的比较、交换的过程。
   整个选择的过程如下图所示：

 

 

 

算法实现：

?
1
2
3
4
5
6
7
8
9
10
11
12
\'\'\'
选择排序
\'\'\'
def Selection_sort(a):
    for i in range(len(a) - 1):
        min = i
        for j in range(i + 1, len(a)):
            if a[min] > a[j]:
                min = j
        if min != i:
            a[min], a[i] = a[i], a[min]
    return a

　　

冒泡排序

介绍：

　　冒泡排序（Bubble Sort，台湾译为：泡沫排序或气泡排序）是一种简单的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。

步骤：

  1. 比较相邻的元素。如果第一个比第二个大，就交换他们两个。
  2. 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。
  3. 针对所有的元素重复以上的步骤，除了最后一个。
  4. 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

 

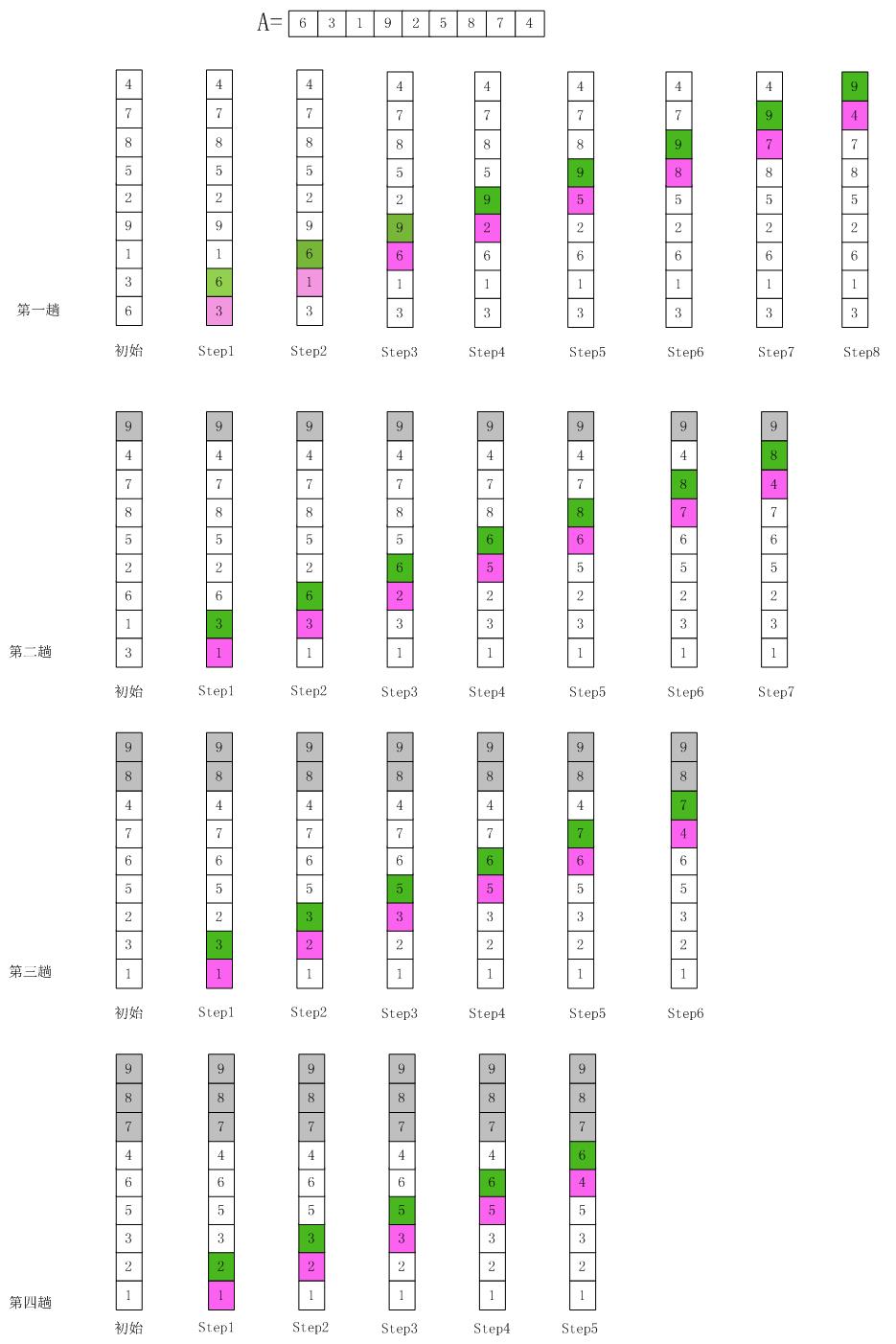
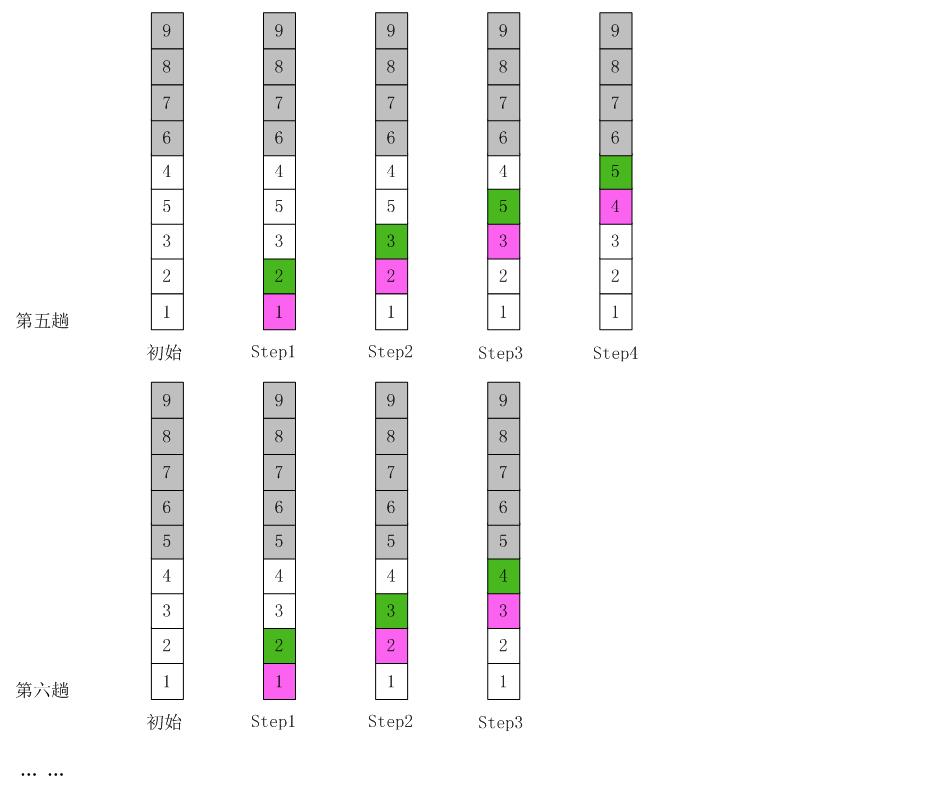
算法实现

?
1
2
3
4
5
6
7
8
9
\'\'\'
冒泡排序
\'\'\'
def Dubble_sort(a):
    for i in range(len(a)):
        for j in range(i+1,len(a)):
            if a[i] > a[j]:
                a[i],a[j] = a[j],a[i]
    return a

插入排序

有一个已经有序的数据序列，要求在这个已经排好的数据序列中插入一个数，但要求插入后此数据序列仍然有序，这个时候就要用到一种新的排序方法——插入排序法,插入排序的基本操作就是将一个数据插入到已经排好序的有序数据中，从而得到一个新的、个数加一的有序数据，算法适用于少量数据的排序，时间复杂度为O(n^2)。是稳定的排序方法。插入算法把要排序的数组分成两部分：第一部分包含了这个数组的所有元素，但将最后一个元素除外（让数组多一个空间才有插入的位置），而第二部分就只包含这一个元素（即待插入元素）。在第一部分排序完成后，再将这个最后元素插入到已排好序的第一部分中。　　

算法实现：

\'\'\'
插入排序
\'\'\'
?
1
2
3
4
5
6
7
8
def Insertion_sort(a):
    for i in range(1,len(a)):
        j = i
        while j>0 and a[j-1]>a[i]:
            j -= 1
        a.insert(j,a[i])
        a.pop(i+1)
    return a

　　

快速排序

介绍：

快速排序（Quicksort）是对冒泡排序的一种改进。在平均状况下，排序 n 个项目要Ο(n log n)次比较。在最坏状况下则需要Ο(n2)次比较，但这种状况并不常见。事实上，快速排序通常明显比其他Ο(n log n) 算法更快，因为它的内部循环（inner loop）可以在大部分的架构上很有效率地被实现出来，且在大部分真实世界的数据，可以决定设计的选择，减少所需时间的二次方项之可能性。

步骤：

  1. 从数列中挑出一个元素，称为 “基准”（pivot），
  2. 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
  3. 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

排序效果：

 

算法实现：

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
\'\'\'
快速排序
\'\'\'
def sub_sort(array,low,high):
    key = array[low]
    while low < high:
        while low < high and array[high] >= key:
            high -= 1
        while low < high and array[high] < key:
            array[low] = array[high]
            low += 1
            array[high] = array[low]
    array[low] = key
    return low
 
 
def quick_sort(array,low,high):
     if low < high:
        key_index = sub_sort(array,low,high)
        quick_sort(array,low,key_index)
        quick_sort(array,key_index+1,high)

　　

然后我们对上面的算法做一个时间比较：

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
\'\'\'\'\'
随机生成0~10000000之间的数值
\'\'\'
def getrandata(num):
    a=[]
    i=0
    while i<num:
        a.append(random.randint(0,10000000))
        i+=1
    return a
 
\'\'\'
随机生成20个长度为10000的数组
\'\'\'
a = []
for i in range(20):
    a.append(getrandata(10000))
 
\'\'\'
测试时间函数
\'\'\'
def time_it(f,a):
    t = []
    for i in range(len(a)):
        t1 = time.time()
        f(a[i])
        t2 = time.time()
        t.append(t2-t1)
    return t
tt1 = time_it(Selection_sort,copy.deepcopy(a))
tt2 = time_it(Dubble_sort,copy.deepcopy(a))
tt3 = time_it(Insertion_sort,copy.deepcopy(a))
tt4 = time_it(Quick_sort,copy.deepcopy(a))
print np.mean(tt1),tt1
print np.mean(tt2),tt2
print np.mean(tt3),tt3
print np.mean(tt4),tt4

　　

在我电脑运行结果如下：

?
1
2
3
4
3.53101536036 [3.1737868785858154, 3.2235000133514404, 3.296314001083374, 3.3746020793914795, 3.6942098140716553, 3.6844170093536377, 3.3293440341949463, 3.6262528896331787, 3.577023983001709, 3.4677979946136475, 3.5323100090026855, 3.3574531078338623, 3.4525561332702637, 3.4662599563598633, 3.8701679706573486, 3.719839096069336, 3.7798891067504883, 3.6078600883483887, 3.803921937942505, 3.582801103591919]
7.22842954397 [7.1081390380859375, 7.365921974182129, 6.666350841522217, 7.258342027664185, 6.8559088706970215, 6.805047035217285, 7.230466842651367, 7.948682069778442, 7.901662111282349, 7.448035955429077, 8.134574890136719, 7.731559991836548, 7.3559558391571045, 6.80467414855957, 7.227035999298096, 6.987092018127441, 6.9657158851623535, 6.997059106826782, 6.9417431354522705, 6.834623098373413]
2.64084545374 [2.6150870323181152, 2.567375898361206, 2.7965359687805176, 2.616096019744873, 2.561455011367798, 2.76595401763916, 2.603566884994507, 2.542672872543335, 2.783787965774536, 2.643486976623535, 2.5308570861816406, 2.764592170715332, 2.6237199306488037, 2.508751153945923, 2.766709089279175, 2.603114128112793, 2.528198003768921, 2.812356948852539, 2.651564836502075, 2.53102707862854]
0.0346855401993 [0.03456306457519531, 0.0337519645690918, 0.03569507598876953, 0.034551143646240234, 0.03506588935852051, 0.03456687927246094, 0.0352480411529541, 0.03591203689575195, 0.03380298614501953, 0.03402996063232422, 0.034184932708740234, 0.03434491157531738, 0.034864187240600586, 0.035611867904663086, 0.03429007530212402, 0.034512996673583984, 0.03453683853149414, 0.03406691551208496, 0.033792972564697266, 0.036318063735961914]

　　

可以看出，快速排序在随机生成的数组中速度上十分有优势。

 

以上是关于经典排序算法及python实现的主要内容，如果未能解决你的问题，请参考以下文章

经典排序算法及python实现

经典排序及总结(python实现)

python实现十大经典排序算法

经典算法之归并排序——python和JS实现

十大经典排序算法（python实现）（原创）

（附代码）动图图解 | 十大经典排序算法Python版实现