回顾
紧接着上篇, 整到了, MES的公式和代码的实现.
\\(MSE = \\frac {1}{n} \\sum\\limits_{i=1}^n (y_i - \\hat y_i)^2\\)
n 表示样本数, 这里为 4
y 表示要预测的变量, 这里是 性别
训练的约束, 就是使得 MSE 的值尽可能小. -> 求解参数
MSE 的工作机制, 举个栗子, 假设网络的纵输出是 0, 也就是预测所有的 小伙伴都是 妹子.
| 姓名 | \\(y_i\\) (真实值) | \\(\\hat y_i\\) (预测值) | \\((y_i - \\hat y_i)\\) |
|---|---|---|---|
| youge | 1 | 0 | 1 |
| share | 1 | 0 | 1 |
| naive | 0 | 0 | 0 |
| beyes | 0 | 0 | 0 |
\\(MSE = \\frac {1}{4} (1 + 1 + 0 + 1) = 0.5\\)
BP算法本质 - 求导链式法则
现在继续...
始终要明确我们的目标: 最小化神经网络的损失 这个损失呢, 本质也就是一个关于 权重和偏置 的函数
如图所示:
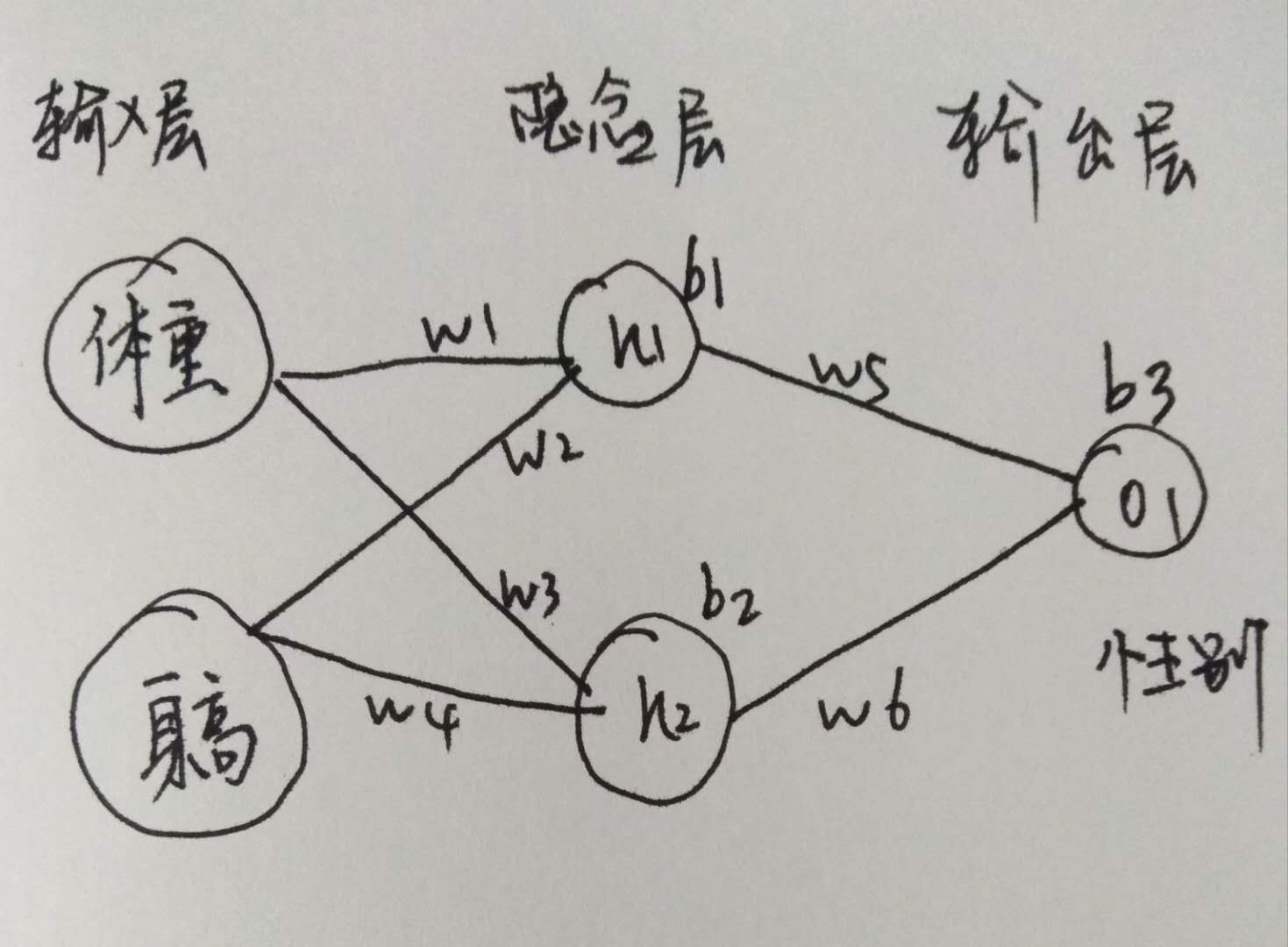
则本例的损失函数可以这样参数化表示为:
\\(L(w_1, w_2, w_3, w_4, w_5, w_6, b1, b_2, b_3)\\)
现在来考虑对 w 进行优化, 假设要优化 \\(w_1\\) (即当 \\(w_1\\) 变化时, L 会如何变化), 也就是: \\(\\frac {\\partial L}{\\partial w_1}\\)
为了简化一波问题, 假设数据集中就只有一个兄弟.
| 姓名 | \\(y_1\\) | \\(\\hat y_1\\) | (\\(y_1 -\\hat y_1\\)) |
|---|---|---|---|
| youge | 1 | 0 | 1 |
则此时的 MSE = \\((y_1 -\\hat y_1)^2 = (1- \\hat y_1)^2\\)
要计算 \\(\\frac {\\partial L}{\\partial w_1}\\) 根据网络的 反向 方向 (输出 -> 输入), 对应选取相应的中间变量, 这样能求出来呀. 根据求导链式法则:
\\(\\frac {\\partial L}{\\partial w_1} = \\frac {\\partial L}{\\partial \\hat y_1} * \\frac {\\partial \\hat y_1}{\\partial w_1}\\)
由本例数据, 已知 \\(L = (1- \\hat y_1)^2\\) , 上面公式的第一部分就可以求出来了:
\\(\\frac {\\partial L} {\\partial y_1} = \\frac {\\partial (1- \\hat y_1)^2} {\\partial y_1} = -2(1- \\hat y_1)\\)
然后是 第二部分 \\(\\frac {\\partial \\hat y_1}{\\partial w_1}\\) 观察图中的相关变量, 可看到 \\(h_1, h_2, o_1\\) 分别表示该神经元的输出, 即:
\\(\\hat y_1 = o_1 = f(w_5 h_1 + w_6 h_2 + b_3)\\)
继续向后传播....

而我们关心的是 \\(w_1\\) , 看图中的线路就可知, w1 跟 h2 是没有关系的, 只跟 h1有关, 于是, 再来一波 求导链式法则
$\\frac {\\partial \\hat y_1}{\\partial w_1} = \\frac {\\partial \\hat y_1} {\\partial h_1} * \\frac {\\partial h_1}{\\partial w_1} $
同样套路, 第一部分
\\(\\frac {\\partial \\hat y_1} {\\partial h_1} = \\frac {f(w_5h_1 + w_6h2 + b_3)} {\\partial h_1} = w_5 * [f\'(w_5h_1 + w_6h2+b_3)]\\)
\\(f\'(w_5h_1 + w_6h2+b_3)\\) 这个其实就 看作 f(x), 里面不论多少项, 都是该 函数的自变量取值而已呀.
对 第二部分 也是一样滴处理
$\\frac {\\partial h_1}{\\partial w_1} = \\frac {f(w_1 x_1 + w_2 x_2 + b_1)} {\\partial w_1} = x_1 * [f\'(w_1x_1 +w_2 x_2 + b_1)] $
终于走到输入值啦, 本例这里的 x_1 是身高, x_2 是体重. 这里的 f(x) 就是咱的 激活函数 (映射实值到0-1)
\\(f(x) = \\frac {1}{1+e^{-x}}\\)
之前推导 逻辑回归的时候, 也是用的这个函数哦, 当时有个技巧点是, 其求导为: \\(f(x)\' = f(x)(1-f(x))\\)
利用 分式 求导法则:
\\(f(x)\' = \\frac {0 - (-e^{-x)}}{(1+e^{-x})^2}\\)
\\(= \\frac {1}{1+e^{-x}} * \\frac {e^{-x}}{1+e^{-x}}\\)
\\(=f(x)(1-f(x))\\)
这个结果在推导逻辑回归的时候, 非常重要的哦, 求一阶导和二阶导都要用到
小结上边的一波操作, 其实就是一个 求导的链式法则:
\\(\\frac {\\partial L}{\\partial w_1} = \\frac {\\partial L}{\\partial \\hat y_1} * \\frac {\\partial \\hat y_1}{\\partial h_1} * \\frac {\\partial h_1}{\\partial w_1}\\)
从网络的方向上来看呢, 是从 output -> input 这样的 反向 误差传递, 这其实就是咱平时说的 BP算法, 而核心就是求导的链式法则而已呀.
所以嘛, 神经网络很多名词, 就是为了唬人, 当你扒开一看, 哦哦, 原来都只是用到一些 基础的数学知识而已
case1: 计算偏导数(Link Rule)
输入(已中心化):
| 姓名 | 体重 | 身高 | 性别 (y) |
|---|---|---|---|
| youge | -2 | 5 | 1 |
输出比较
| 姓名 | \\(y_i\\) | \\(\\hat y_1\\) | (\\(y_1 -\\hat y_1\\)) |
|---|---|---|---|
| youge | 1 | 0 | 1 |
同样, 为计算更加方便, 假设所有的 权重 为1, 所有的偏置为 0
\\(h_1 = f(w_1 x_1 + w_2 x_2 + b_1)\\)
\\(= f(-2 + 5 + 0)\\)
\\(=f(3) = 0.952\\)
继续,
\\(h_2 = f(w_3x_1 + w_4 x_2 + b_2)\\)
\\(= f(-2 + 5 + 0) = h_1 = 0.952\\)
继续,
\\(o_1 = f(w_5h_1 + w_6h_2 + b3)\\)
\\(=f(0.952 + 0.952 + 0) = 0.871\\)
即本例的网络输出是 \\(\\hat y_1 = 0.871\\) 比较有倾向性的哦, 计算来算一下 \\(\\frac {\\partial L}{\\partial w_1}\\) 应用上面的结论.
\\(\\frac {\\partial L}{\\partial w_1} = \\frac {\\partial L}{\\partial \\hat y_1} * \\frac {\\partial \\hat y_1}{\\partial h_1} * \\frac {\\partial h_1}{\\partial w_1}\\)
同样分解为 3个部分:
\\(\\frac {\\partial L}{\\partial \\hat y_1} = -2(1- \\hat y_1)\\)
\\(= -2(1-0.871)\\)
\\(=-0.258\\)
继续...
$ \\frac {\\partial \\hat y_1}{\\partial h_1} = \\frac {f(w_5h_1 + w_6h2 + b_3)} {\\partial h_1} = x_1 * [f\'(w_5h_1 + w_6h2+b_3)]$
\\(=(-2) * f\'(0.952 +0.952+0)\\)
\\(=(-2) * [f(1.904) \\ f(1-1.904)]\\)
\\(= -0.502\\)
继续...
\\(\\frac {\\partial h_1}{\\partial w_1} = \\frac {f(w_1 x_1 + w_2 x_2 + b_1)} {\\partial w_1} = x_1 * [f\'(w_1x_1 +w_2 x_2 + b_1)]\\)
\\(=(-2) * f\'(-2 + 5 + 0)\\)
\\(= -2 *f\'(3)\\)
\\(=-2 * f(3) \\ f(1-3)\\)
\\(=-0.227\\)
因此
\\(\\frac {\\partial L}{\\partial w_1} = (-0.258) * (-0.502) * (-0.227)\\)
\\(=-0.029\\)
意义: 随着 w_1 的增加, 损失 L 会随着减少.
随机梯度减小(SGD)
本质就是更新参数 w, 沿着 梯度的反方向微调一个步长, 直到算法收敛 或者 是随机选择一个样本, 每次做更迭,, 求解出最优的权重参数向量 w

\\(w \\leftarrow w_1 - \\alpha \\ \\frac {\\partial L}{\\partial w_1}\\)
这个 \\(\\alpha\\) 也称为 学习率, 也就是步长呗, 或者速率都可以的, 理解上面这句话是最关键的.
为啥是沿着 梯度的反向方, 这个涉及方向导数这一块的, 自己看大一的高数吧, 懒得解释了.
- \\(\\frac {\\partial L}{\\partial w_1}\\) 偏导数 大于0, 则说明要将 w_1 调小, 使得 L 变小
- \\(\\frac {\\partial L}{\\partial w_1}\\) 偏导数 小于0, 则说明要将 w_1 调大, 使得 L 变小
因为网络中有 多个 w_i 嘛, 如果我们对每一个 w_i 都 进行这样的优化, 则整个网络的损失则会不断下降, 也就意味着网络的预测性能在不断地上升.
训练过程
-
从数据集中随机选取一个样本, 用 SGD 进行优化, (每次只针对一个样本进行优化)
-
计算每个权重 w_i 和 偏置 bias, ( 计算 \\(\\frac {\\partial L}{\\partial w_1}, \\frac {\\partial L}{\\partial w_2} ... b_1, b_2...\\)) 等
-
更新权重和bias
-
重复 第一步 .... 直到将所有的样本遍历完
代码实现 - 完整的神经网络
| 姓名 | 体重 | 身高 | 性别 (y) |
|---|---|---|---|
| youge | -2 | 5 | 1 |
| share | -5 | -2 | 1 |
| naive | -23 | -11 | 0 |
| beyes | 30 | 8 | 0 |

从网上抄的代码, 这个难度不大代码, 就懒得写了, 学会抄, 和改, 我感觉是提升工作能力的必要能力.
import numpy as np
class Network:
def __init__(self):
# 本例的权重w
self.w1 = np.random.normal()
self.w2 = np.random.normal()
self.w3 = np.random.normal()
self.w4 = np.random.normal()
self.w5 = np.random.normal()
self.w6 = np.random.normal()
# 偏置 bias
self.b1 = np.random.normal()
self.b2 = np.random.normal()
self.b3 = np.random.normal()
def sigmoid(self, x):
"""激活函数, 映射一个实值到 [0,1]"""
return 1 / (1 + np.exp(-x))
def der_of_sigmoid(self, x):
"""激活函数的导数"""
f = self.sigmoid # 地址引用
return f(x) * (1 - f(x))
@staticmethod
def mes_loss(y_true, y_predict):
"""
计算均方误差
:param y_true, arr 真实样本值组成的array
:param y_predict, arr 预测样本值组成的array
:return: float, 总损失
"""
return ((y_true - y_predict) ** 2).mean()
def feedforward(self, arr):
"""前向算法, arr是一个2个特征的数组"""
h1 = self.sigmoid(self.w1 * arr[0] + self.w2 * arr[1] + self.b1)
h2 = self.sigmoid(self.w3 * arr[0] + self.w4 * arr[1] + self.b2)
o1 = self.sigmoid(self.w5 * h1 + self.w6 * h2 + self.b3)
def train(self, data, all_y_true):
"""根据训练数据, 求解参数"""
learn_rate = 0.1
max_iter = 1000
for i in range(max_iter):
for x, y_true in zip(data, all_y_true):
sum_h1 = self.w1 * x[0] + self.w2 * x[1] + self.b1
h1 = self.sigmoid(sum_h1)
sum_h2 = self.w3 * x[0] + self.w4 * x[1] + self.b2
h2 = self.sigmoid(sum_h2)
sum_o1 = self.w5 * h1 + self.w6 * h2 + self.b3
o1 = self.sigmoid(sum_o1)
y_pred = o1
d_L_d_ypred = -2 * (y_true - y_pred)
# o1
d_ypred_d_w5 = h1 * self.der_of_sigmoid(sum_o1)
d_ypred_d_w6 = h2 * self.der_of_sigmoid(sum_o1)
d_ypred_d_b3 = self.der_of_sigmoid(sum_o1)
d_ypred_d_h1 = self.w5 * self.der_of_sigmoid(sum_o1)
d_ypred_d_h2 = self.w6 * self.der_of_sigmoid(sum_o1)
# h1
d_h1_d_w1 = x[0] * self.der_of_sigmoid(sum_h1)
d_h1_d_w2 = x[1] * self.der_of_sigmoid(sum_h1)
d_h1_d_b1 = self.der_of_sigmoid(sum_h1)
# h2
d_h1_d_w3 = x[0] * self.der_of_sigmoid(sum_h2)
d_h1_d_w4 = x[1] * self.der_of_sigmoid(sum_h2)
d_h1_d_b2 = self.der_of_sigmoid(sum_h2)
# 应用梯度下降, 更新 权重值 和 bias
# h1
self.w1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w1
self.w2 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w2
self.b1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_b1
# h2
self.w3 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w3
self.w4 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w4
self.b2 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_b2
# o1
self.w5 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_ypred_d_w5
self.w6 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_ypred_d_w6
self.b3 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_ypred_d_b3
# 计算总的损失 Loss
if i % 10 == 0:
y_preds = np.apply_along_axis(self.feedforward, 1, data)
loss = self.mes_loss(all_y_true, y_preds)
print("Epoch %d loss: %.3f" % (i, loss))
if __name__ == \'__main__\':
# test
data = np.array([
[-2, 5],
[-5, -2],
[-23, -11],
[30, 8]
])
all_y_trues = np.array([1, 1, 0, 0])
# 训练神经网络
neework = Network()
neework.train(data, all_y_trues)
没有debug 哦, 绝大部分都不是我自己的代码, 目的是做个笔记参考而已, 参考思路而非真正用这样而代码做生产.