用Python在地图上模拟疫情扩散

Posted 2021-03-12 Wind·Chaser

最近在研究热力图，发现了一篇可能有用的Python模拟疫情扩散的文章，可以部分模拟热力图，整篇文章原文内容如下：

瘟疫蔓延，连芬兰都难以幸免

受杰森的《Almost Looks Like Work》启发，我来展示一些病毒传播模型。需要注意的是这个模型并不反映现实情况，因此不要误以为是西非可怕的传染病。相反，它更应该被看做是某种虚构的僵尸爆发现象。那么，让我们进入主题。

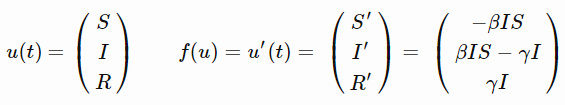
这就是SIR模型，其中字母S、I和R反映的是在僵尸疫情中，个体可能处于的不同状态。

• S 代表易感群体，即健康个体中潜在的可能转变的数量。

• I 代表染病群体，即僵尸数量。

• R 代表移除量，即因死亡而退出游戏的僵尸数量，或者感染后又转回人类的数量。但对与僵尸不存在治愈者，所以我们就不要自我愚弄了（如果要把SIR模型应用到流感传染中，还是有治愈者的）。

至于β(beta)和γ(gamma):

• β(beta)表示疾病的传染性程度，只要被咬就会感染。

• γ(gamma)表示从僵尸走向死亡的速率，取决于僵尸猎人的平均工作速率，当然，这不是一个完美的模型，请对我保持耐心。

S′=−βIS告诉我们健康者变成僵尸的速率，S′是对时间的导数。

I′=βIS−γI告诉我们感染者是如何增加的，以及行尸进入移除态速率（双关语）。

R′=γI只是加上(gamma I)，这一项在前面的等式中是负的。

上面的模型没有考虑S/I/R的空间分布，下面来修正一下！

一种方法是把瑞典和北欧国家分割成网格，每个单元可以感染邻近单元，描述如下：

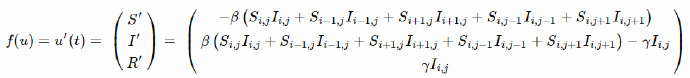
其中对于单元，和是它周围的四个单元。（不要因为对角单元而脑疲劳，我们需要我们的大脑不被吃掉）。

初始化一些需要的库以及数据

 1 import numpy as np
 2 import math
 3 import matplotlib.pyplot as plt
 4  
 5 from matplotlib import rcParams
 6 import matplotlib.image as mpimg
 7 rcParams[‘font.family‘] = ‘serif‘
 8 rcParams[‘font.size‘] = 16
 9 rcParams[‘figure.figsize‘] = 12, 8
10 from PIL import Image

适当的beta和gamma值就能够摧毁大半江山

1 beta = 0.010
2 gamma = 1

还记得导数的定义么？当导数已知，假设Δt很小的情况下，经过重新整理，它可以用来近似预测函数的下一个取值，我们已经声明过u′(t)。

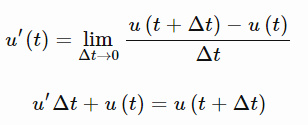
回想前面：

我们把函数(u(t +△t))在下一个时间步记为，表示当前时间步。

这种方法叫做欧拉法，代码如下：

1 def euler_step(u, f, dt):
2     return u + dt * f(u)

我们需要函数f(u)。友好的numpy提供了简洁的数组操作。我可能会在另一篇文章中回顾它，因为它们太强大了，需要更多的解释，但现在这样就能达到效果：

 1 def f(u):
 2     S = u[0]
 3     I = u[1]
 4     R = u[2]
 5  
 6     new = np.array([-beta*(S[1:-1, 1:-1]*I[1:-1, 1:-1] +
 7                             S[0:-2, 1:-1]*I[0:-2, 1:-1] +
 8                             S[2:, 1:-1]*I[2:, 1:-1] +
 9                             S[1:-1, 0:-2]*I[1:-1, 0:-2] +
10                             S[1:-1, 2:]*I[1:-1, 2:]),
11                      beta*(S[1:-1, 1:-1]*I[1:-1, 1:-1] +
12                             S[0:-2, 1:-1]*I[0:-2, 1:-1] +
13                             S[2:, 1:-1]*I[2:, 1:-1] +
14                             S[1:-1, 0:-2]*I[1:-1, 0:-2] +
15                             S[1:-1, 2:]*I[1:-1, 2:]) - gamma*I[1:-1, 1:-1],
16                      gamma*I[1:-1, 1:-1]
17                     ])
18  
19     padding = np.zeros_like(u)
20     padding[:,1:-1,1:-1] = new
21     padding[0][padding[0] < 0] = 0
22     padding[0][padding[0] > 255] = 255
23     padding[1][padding[1] < 0] = 0
24     padding[1][padding[1] > 255] = 255
25     padding[2][padding[2] < 0] = 0
26     padding[2][padding[2] > 255] = 255
27  
28     return padding

导入北欧国家的人口密度图并进行下采样，以便较快地得到结果

1 from PIL import Image
2 img = Image.open(‘popdens2.png‘)
3 img = img.resize((img.size[0]/2,img.size[1]/2))
4 img = 255 - np.asarray(img)
5 imgplot = plt.imshow(img)
6 imgplot.set_interpolation(‘nearest‘)

北欧国家的人口密度图（未包含丹麦）

S矩阵，也就是易感个体，应该近似于人口密度。感染者初始值是0，我们把斯德哥尔摩作为第一感染源。

1 S_0 = img[:,:,1]
2 I_0 = np.zeros_like(S_0)
3 I_0[309,170] = 1 # patient zero

因为还没人死亡，所以把矩阵也置为0.

1 R_0 = np.zeros_like(S_0)

接着初始化模拟时长等。

 1 T = 900                         # final time
 2 dt = 1                          # time increment
 3 N = int(T/dt) + 1               # number of time-steps
 4 t = np.linspace(0.0, T, N)      # time discretization
 5  
 6 # initialize the array containing the solution for each time-step
 7 u = np.empty((N, 3, S_0.shape[0], S_0.shape[1]))
 8 u[0][0] = S_0
 9 u[0][1] = I_0
10 u[0][2] = R_0

我们需要自定义一个颜色表，这样才能将感染矩阵显示在地图上。

1 import matplotlib.cm as cm
2 theCM = cm.get_cmap("Reds")
3 theCM._init()
4 alphas = np.abs(np.linspace(0, 1, theCM.N))
5 theCM._lut[:-3,-1] = alphas

下面坐下来欣赏吧…

1 for n in range(N-1):
2     u[n+1] = euler_step(u[n], f, dt)

让我们再做一下图像渲染，把它做成gif，每个人都喜欢gifs！

 1 from images2gif import writeGif
 2  
 3 keyFrames = []
 4 frames = 60.0
 5  
 6 for i in range(0, N-1, int(N/frames)):
 7     imgplot = plt.imshow(img, vmin=0, vmax=255)
 8     imgplot.set_interpolation("nearest")
 9     imgplot = plt.imshow(u[i][1], vmin=0, cmap=theCM)
10     imgplot.set_interpolation("nearest")
11     filename = "outbreak" + str(i) + ".png"
12     plt.savefig(filename)
13     keyFrames.append(filename)
14  
15 images = [Image.open(fn) for fn in keyFrames]
16 gifFilename = "outbreak.gif"
17 writeGif(gifFilename, images, duration=0.3)
18 plt.clf()

瘟疫蔓延的gif图，连芬兰都难以幸免

看，唯一安全的地方是人口密度不太高的北部地区，动画中连芬兰最后都被感染了，现在你明白了吧。

如果你想了解更多微分方程的求解，温馨向您推荐LorenaABarba 的实用数值方法的Python实现课程，你可以从中学习所有实数的数值求解方法，而不是本文中简单的这种。

更新：你可以在这里找到Ipython版本的笔记。

实际运行上面的例子的代码是存在问题的，往往会编译不通过，下面是经过调整后的代码例子，可以正常运行：

上图是代码需要的图片popdens2.png

具体的代码：

import numpy as np
import math
import matplotlib.pyplot as plt
 
from matplotlib import rcParams
import matplotlib.image as mpimg
rcParams[‘font.family‘] = ‘serif‘
rcParams[‘font.size‘] = 16
rcParams[‘figure.figsize‘] = 12, 8
from PIL import Image
 
beta = 0.010
gamma = 1
 
def euler_step(u, f, dt):
    return u + dt * f(u)
 
def f(u):
    S = u[0]
    I = u[1]
    R = u[2]
 
    new = np.array([-beta*(S[1:-1, 1:-1]*I[1:-1, 1:-1] +
                            S[0:-2, 1:-1]*I[0:-2, 1:-1] +
                            S[2:, 1:-1]*I[2:, 1:-1] +
                            S[1:-1, 0:-2]*I[1:-1, 0:-2] +
                            S[1:-1, 2:]*I[1:-1, 2:]),
                     beta*(S[1:-1, 1:-1]*I[1:-1, 1:-1] +
                            S[0:-2, 1:-1]*I[0:-2, 1:-1] +
                            S[2:, 1:-1]*I[2:, 1:-1] +
                            S[1:-1, 0:-2]*I[1:-1, 0:-2] +
                            S[1:-1, 2:]*I[1:-1, 2:]) - gamma*I[1:-1, 1:-1],
                     gamma*I[1:-1, 1:-1]
                    ])
 
    padding = np.zeros_like(u)
    padding[:,1:-1,1:-1] = new
    padding[0][padding[0] < 0] = 0
    padding[0][padding[0] > 255] = 255
    padding[1][padding[1] < 0] = 0
    padding[1][padding[1] > 255] = 255
    padding[2][padding[2] < 0] = 0
    padding[2][padding[2] > 255] = 255
 
    return padding
 
 
from PIL import Image
img = Image.open(‘popdens2.png‘)
img = img.resize((img.size[0]/2,img.size[1]/2))
img = 255 - np.asarray(img)
imgplot = plt.imshow(img)
imgplot.set_interpolation(‘nearest‘)
 
S_0 = img[:,:,1]
I_0 = np.zeros_like(S_0)
I_0[309,170] = 1 # patient zero
 
R_0 = np.zeros_like(S_0)
 
 
T = 900                         # final time
dt = 1                          # time increment
N = int(T/dt) + 1               # number of time-steps
t = np.linspace(0.0, T, N)      # time discretization
 
# initialize the array containing the solution for each time-step
u = np.empty((N, 3, S_0.shape[0], S_0.shape[1]))
u[0][0] = S_0
u[0][1] = I_0
u[0][2] = R_0
 
import matplotlib.cm as cm
theCM = cm.get_cmap("Reds")
theCM._init()
alphas = np.abs(np.linspace(0, 1, theCM.N))
theCM._lut[:-3,-1] = alphas
 
for n in range(N-1):
    u[n+1] = euler_step(u[n], f, dt)
 
keyFrames = []
frames = 60.0
 
for i in range(0, N-1, int(N/frames)):
    imgplot = plt.imshow(img, vmin=0, vmax=255)
    imgplot.set_interpolation("nearest")
    imgplot = plt.imshow(u[i][1], vmin=0, cmap=theCM)
    imgplot.set_interpolation("nearest")
    filename = "outbreak" + str(i) + ".png"
    plt.savefig(filename)
    keyFrames.append(filename)
 
import imageio  
  
def create_gif(image_list, gif_name,gif_duration=0.1):  
  
    frames = []  
    for image_name in image_list:  
        frames.append(imageio.imread(image_name))  
    # Save them as frames into a gif  
    imageio.mimsave(gif_name, frames, ‘GIF‘, duration = gif_duration)
 
 
image_list=keyFrames
gif_name = ‘zombie.gif‘
create_gif(image_list, gif_name,gif_duration=0.3)  
plt.clf()

参考链接

---

• 用Python在地图上模拟疫情扩散
• [python图像处理] gif动态图的解析与合成
• AttributeError: ‘numpy.ndarray‘ object has no attribute ‘tobytes‘ 
• maxberggren/blog-notebooks
• 用Python和MoviePy将数据动态可视化
• 用Python在地图上模拟疫情扩散