逻辑回归的原理和python实现

Posted 2021-03-09 ming_tian0826

输入

　　鸢尾花卉数据集,数据集包含150个数据样本，分为3类，每类50个数据，每个数据包含4个属性。

输出

　　根据手动实现的逻辑回归模型对鸢尾花卉数据集分类的预测结果。

原理

　　逻辑回归处理的是分类问题，线性回归处理的是回归问题，这是两者最本质的区别。逻辑回归算法是一种分类算法，适用于标签取值离散的情况。

　　逻辑回归的模型为：

　　　　　　　　　　　　　　　

　　其中，代表特征向量，代表逻辑函数，一个常用的逻辑函数公式为：

　　　　　　　　　　　　　　　　

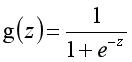
　　该函数的图像为：

 

　　

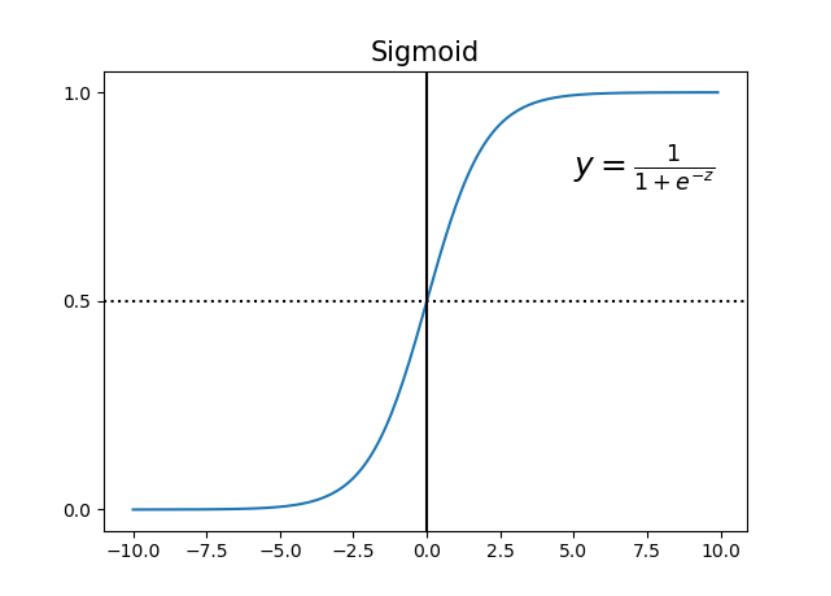
　　通过公式和图像，我们可以总结下的作用：对于给定的输入变量，根据选择的参数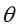计算输出变量等于1的概率，即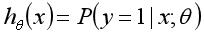，比如给定的变量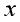，通过给定的参数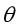计算得到 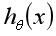= 0.7，则表示有70%的几率输出变量为正向类，30%的几率为负向类。

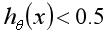　　在逻辑回归中，当时，预测y=1，当时，预测y=0。而这两种情况分别对应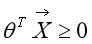、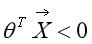，在几何上意味着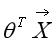是真正意义上的分界边界函数，常见的比如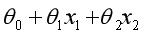：（线性分界函数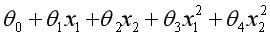）、（二次分界函数）。在实际的业务场景中，可以选择复杂的分界函数来处理数据。

当分解函数选定之后，有一个非常重要的操作是确定逻辑回归模型的参数，按照机器学习的思路，我们要定义代价函数，通过梯度下降法更新参数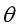，最小化代价函数来得到参数。

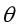在线性回归模型中，采用的代价函数为所有样本误差的平方和，那是因为此时的代价函数是凸函数，一定会得到一个最小值。如果逻辑回归模型采用所有样本误差的平方和作为代价函数，那么得到的代价函数是非凸的，非凸函数有很多的极小值点，影响梯度下降法寻找全局最小值。

根据逻辑回归处理的分类问题本质上只有正、负样本的特性，我们定义逻辑回归的代价函数为：

　　　　　　　　　　　　

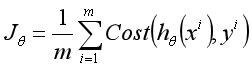
其中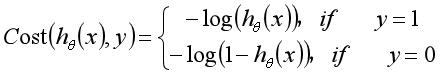，，其实这么定义也比较容易理解，比如对于一个y=1的正样本，由于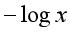是一个在作用域(0,1]上从正无穷大递减至0的函数，如果sigmoid函数模型预测的概率比较小，接近于0，预测为负样本，那么代价函数值就比较大，如果sigmoid函数模型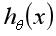预测的概率比较大，接近于1，预测为正样本，那么代价就比较小，如果概率为1的话，代价函数值就为0了，这不就刚好是我们想要的吗？同理可理解对于y=0时采用的代价函数。

我们将代价函数整理如下：

针对每个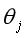求偏导得到：

　　有了偏导之后，就可以更新参数：

　　　　　　

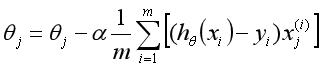
在训练的过程中，有可能遇到到过拟合的问题，我们可以使用正则化的技术来较少过拟合的影响，我们对参数做适当的惩罚，优化代价函数为：

　　

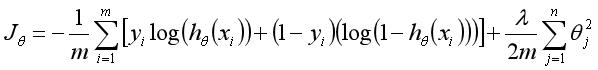
这里注意到，我们一般不对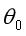做惩罚。

　　同时，由于偏导有了改变，更新参数也需要对应改变：

　　　　　　　　　　　　

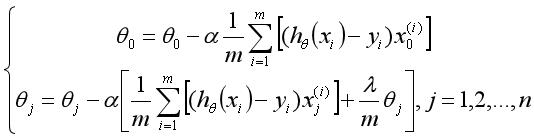
这样我们就可以通过最小化代价函数，一步步更新参数，拟合出想要的参数了，得到一个逻辑回归分类器，但是如果我们处理的是多分类问题该怎么办呢？

　　假如我们处理的是一个三分类问题，有三个类别0，1，2。我们可以构造3个分类器：

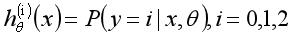
那么如何构造这些分类器呢？我们以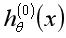为例，在构造这个分类器时，标签类别为0的样本为正样本对应的y修改为1，其余的标签类别非0的样本为负样本对应的y修改为0，这样处理之后进行训练就可以得到一个可以分类0类别与非0类别的分类器了，同理另外两个分类器也可得到。

得到3个分类器后，对于一个样本而言，如何生成最终的类别呢？我们可以让三个分类器分别作用于该样本，值最大的分类器为最终的分类结果。

Python代码实现

  1 import pandas as pd
  2 import numpy as np
  3 from sklearn.model_selection import train_test_split
  4 
  5 # 鸢尾花卉数据集,数据集包含150个数据样本，分为3类，每类50个数据，每个数据包含4个属性。
  6 # 可通过花萼长度，花萼宽度，花瓣长度，花瓣宽度4个属性预测鸢尾花卉属于（Setosa，Versicolour，Virginica）三个种类中的哪一类。
  7 iris_path = \'./iris.csv\'
  8 iris_data = pd.read_csv(iris_path)
  9 
 10 # 将字符串标签映射为int
 11 def iris_str_to_int(str):
 12     label = {\'setosa\':0, \'versicolor\':1, \'virginica\':2}
 13     return label[str]
 14 new_iris_data = pd.io.parsers.read_csv(iris_path, converters={4:iris_str_to_int})
 15 data = np.array(new_iris_data)
 16 
 17 # 对数据进行归一化
 18 for col in range(0, len(data[0]) - 1):
 19     mean = np.mean(data[:, col])
 20     std = np.std(data[:, col])
 21     data[:, col] = data[:, col] - mean
 22     data[:, col] = data[:, col] / std
 23 
 24 # 划分数据集,30%测试集、70%训练集,使用sklearn的train_test_split方法
 25 x, y = np.split(data, (4,), axis=1)
 26 x_train, x_test, y_train, y_test = train_test_split(x,y,test_size = 0.3)
 27 
 28 # sigmoid方法
 29 def sigmoid(x):
 30     return 1.0/(1+np.exp(-x))
 31 
 32 # 修改目标y值时使用的方法，因为是多分类，在训练时需要保证只有正类、负类两类
 33 def func(value,lb):
 34     if any(value == lb):
 35         value = 1
 36     else:
 37         value = 0
 38     return value
 39 
 40 # 选择线性模型(theta_0 + theta_1 * x1 + theta_2 * x2 + ...)来做逻辑回归
 41 # 因为有三类，所以要构造3个分类器，即为h0, h1, h2
 42 # 根据入参的标签值，来对y进行修改，
 43 # 比方说，如果label = 0，说明这是h0分类器，那么y == 0为正样本（y值应从0修改为1)，其他非0的修改为负样本（y值应修改为0）
 44 # 如果label = 1，说明这是h1分类器，那么y == 1为正样本（y值应从1修改为1)，其他非1的修改为负样本（y值应修改为0）
 45 # 如果label = 2，说明这是h2分类器，那么y中2为正样本（y值应从2修改为1)，其他非2的修改为负样本（y值应修改为0）
 46 alpha = np.random.random() #学习率
 47 lamda = np.random.random() #正则化系数
 48 theta = np.random.rand(5) # theta参数初始值
 49 print(\'init alpha:{}, lamda:{}, theta:{}\'.format(alpha, lamda, theta))
 50 def cost_line_reg(theta, x, y, label):
 51     theta = np.mat(theta)
 52 
 53     # x特征向量加一个元素x0，x0 == 1
 54     x_one = np.ones(x.shape[0])
 55     x = np.insert(x, 0, values= x_one, axis=1)
 56     x = np.mat(x)
 57 
 58     # 根据label参数指定的分类器种类，对应修改y值
 59     y = np.apply_along_axis(func, axis=1, arr=y, lb=label)
 60     y = np.mat(y)
 61 
 62     # 计算损失值和更新theta
 63     for step in range(0,100):
 64         first = np.multiply((-y).T, np.log(sigmoid(np.dot(x, theta.T))))
 65         second = np.multiply((1-y).T, np.log(1 - sigmoid(np.dot(x, theta.T))))
 66         reg = (lamda/(2*len(x)) * np.sum(np.power(theta[:, 1:theta.shape[1]], 2)))
 67         cost = np.sum(first - second) / (len(x)) + reg
 68 
 69         # 更新theta
 70         for theta_index in range(0, len(theta.T)):
 71             h_theta = sigmoid(np.dot(x, theta.T))
 72             sum = np.dot((h_theta.T - y), x[:, theta_index : theta_index + 1])
 73             sum = np.sum(sum)/len(x)
 74 
 75             # theta0 与 其他的theta元素更新方式有点差异
 76             if theta_index == 0:
 77                 theta[0,theta_index] = theta[0,theta_index] - alpha * sum
 78             else:
 79                 theta[0, theta_index] = theta[0, theta_index] - alpha * (sum + lamda/len(x) * theta[0, theta_index])
 80 
 81     return np.array(theta)
 82 
 83 theta_result_h0 = cost_line_reg(theta, x_train, y_train, 0) # h0 分类器
 84 theta_result_h1 = cost_line_reg(theta, x_train, y_train, 1) # h1 分类器
 85 theta_result_h2 = cost_line_reg(theta, x_train, y_train, 2) # h2 分类器
 86 
 87 print(\'theta_result_h0:{}\'.format(theta_result_h0))
 88 print(\'theta_result_h1:{}\'.format(theta_result_h1))
 89 print(\'theta_result_h2:{}\'.format(theta_result_h2))
 90 
 91 # h0,h1,h2三个分类器确定好之后，把生成结果最大的分类器作为最终分类
 92 # 输入是特征向量，返回的是分类结果
 93 def h_theta(x_arr):
 94 
 95     # 这里默认三个分类器的分界函数都是线性的
 96     h0_result = sigmoid(np.dot(x_arr , theta_result_h0.T))
 97     h1_result = sigmoid(np.dot(x_arr, theta_result_h1.T))
 98     h2_result = sigmoid(np.dot(x_arr , theta_result_h2.T))
 99     # 结果最大的分类器作为最终分类
100     result_lable = 0
101     if h0_result > h1_result and h0_result > h2_result:
102         result_lable = 0
103     elif h1_result > h0_result and h1_result > h2_result:
104         result_lable = 1
105     elif h2_result > h0_result and h2_result > h1_result:
106         result_lable = 2
107     return result_lable
108 
109 # 在数据集上进行测试
110 def verify(x, y):
111     x_one = np.ones(x.shape[0])
112     x = np.insert(x, 0, values= x_one, axis=1)
113     x = np.mat(x)
114 
115     # 各个真实类别的统计个数
116     y_real_0_num = 0
117     y_real_1_num = 0
118     y_real_2_num = 0
119 
120     # 各个真实类别等于预测类别的统计个数
121     y_real_0_prediction_0_num = 0
122     y_real_1_prediction_1_num = 0
123     y_real_2_prediction_2_num = 0
124 
125     # 各类别的预测准确度
126     accuracy_rite_0 = 0.0
127     accuracy_rite_1 = 0.0
128     accuracy_rite_2 = 0.0
129     accuracy_rite_whole = 0.0
130 
131     for row in range(0, len(x)):
132         x_arr = x[row,:]
133         y_real = y[row,0]
134         y_prediction = h_theta(x_arr)
135 
136         # 统计各个真实类别的个数
137         if y_real == 0:
138             y_real_0_num = y_real_0_num + 1
139         elif y_real == 1:
140             y_real_1_num = y_real_1_num + 1
141         elif y_real == 2:
142             y_real_2_num = y_real_2_num + 1
143 
144         # 统计各个真实类别等于预测类别的个数
145         if y_real == 0 and y_prediction == 0:
146             y_real_0_prediction_0_num = y_real_0_prediction_0_num + 1
147         elif y_real == 1 and y_prediction == 1:
148             y_real_1_prediction_1_num = y_real_1_prediction_1_num + 1
149         elif y_real == 2 and y_prediction == 2:
150             y_real_2_prediction_2_num = y_real_2_prediction_2_num + 1
151 
152     print(\'y_real_0_prediction_0_num[{}],y_real_0_num[{}], y_real_1_prediction_1_num[{}], y_real_1_num[{}], y_real_2_prediction_2_num[{}], y_real_2_num[{}]\'
153                  .format(y_real_0_prediction_0_num, y_real_0_num, y_real_1_prediction_1_num, y_real_1_num, y_real_2_prediction_2_num, y_real_2_num))
154 
155     accuracy_rite_0 = y_real_0_prediction_0_num / y_real_0_num
156     accuracy_rite_1 = y_real_1_prediction_1_num / y_real_1_num
157     accuracy_rite_2 = y_real_2_prediction_2_num / y_real_2_num
158     accuracy_rite_whole = (y_real_0_prediction_0_num + y_real_1_prediction_1_num + y_real_2_prediction_2_num) / (len(x))
159     print(\'accuracy_rite_0[{}], accuracy_rite_1[{}], accuracy_rite_2[{}], accuracy_rite_whole[{}]\'.format(accuracy_rite_0, accuracy_rite_1, accuracy_rite_2, accuracy_rite_whole))
160 print(\'############## train_verify begin ##########\')
161 verify(x_train, y_train)
162 print(\'############## train_verify end ##########\')
163 print(\'############## test_verify begin ##########\')
164 verify(x_test, y_test)
165 print(\'############## test_verify end ##########\')

代码运行结果

　　本文档重点在于讨论逻辑回归的原理和实现，所以代码里面的一些参数是随机生成的，每次执行的结果会有少许差异，工业环境中要对参数进行调优，选择最优化的参数。

　　执行程序，产生的测试结果如下：

 1 init alpha:0.9878106271950878, lamda:0.07590602610318298, theta:[0.09612366 0.49599455 0.38297285 0.9730732  0.54394658]
 2 theta_result_h0:[[-1.91985969 -1.42605078  1.81454853 -1.74542862 -1.84684359]]
 3 theta_result_h1:[[-0.93718773  0.49878395 -1.18385395  0.59397282 -0.81950924]]
 4 theta_result_h2:[[-3.40965892  0.07144545 -0.59527357  2.66257363  2.65466814]]
 5 ############## train_verify begin ##########
 6 y_real_0_prediction_0_num[39],y_real_0_num[39], y_real_1_prediction_1_num[29], y_real_1_num[33], y_real_2_prediction_2_num[30], y_real_2_num[33]
 7 accuracy_rite_0[1.0], accuracy_rite_1[0.8787878787878788], accuracy_rite_2[0.9090909090909091], accuracy_rite_whole[0.9333333333333333]
 8 ############## train_verify end ##########
 9 ############## test_verify begin ##########
10 y_real_0_prediction_0_num[11],y_real_0_num[11], y_real_1_prediction_1_num[16], y_real_1_num[17], y_real_2_prediction_2_num[17], y_real_2_num[17]
11 accuracy_rite_0[1.0], accuracy_rite_1[0.9411764705882353], accuracy_rite_2[1.0], accuracy_rite_whole[0.9777777777777777]
12 ############## test_verify end ##########