机器学习算法的基本知识（使用Python和R代码）

Posted lijianming180

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了机器学习算法的基本知识（使用Python和R代码）相关的知识，希望对你有一定的参考价值。


本篇文章是原文的译文，然后自己对其中做了一些修改和添加内容（随机森林和降维算法）。文章简洁地介绍了机器学习的主要算法和一些伪代码，对于初学者有很大帮助，是一篇不错的总结文章，后期可以通过文中提到的算法展开去做一些实际问题。

Google的自驾车和机器人得到了很多新闻，但公司的真正未来是机器学习，这种技术使计算机变得更智能，更个性化。-Eric Schmidt (Google Chairman)

我们可能生活在人类历史上最具影响力的时期——计算从大型主机到PC移动到云计算的时期。 但是使这段时期有意义的不是发生了什么，而是在未来几年里我们的方式。

这个时期令像我这样的一个人兴奋的就是，随着计算机的推动，工具和技术的民主化。 今天，作为数据科学家，我可以每小时为几个玩偶构建具有复杂算法的数据处理机。 但到达这里并不容易，我已经度过了许多黑暗的日日夜夜。

谁可以从本指南中获益最多

我今天发布的可能是我创造的最有价值的指南。

创建本指南背后的理念是简化全球有抱负的数据科学家和机器学习爱好者的旅程。 本指南能够使你在研究机器学习问题的过程中获取经验。 我提供了关于各种机器学习算法以及R＆Python代码的高级理解以及运行它们，这些应该足以使你得心顺手。
技术图片
我故意跳过了这些技术背后的统计数据，因为你不需要在开始时就了解它们。 所以，如果你正在寻找对这些算法的统计学理解，你应该看看别的文章。 但是，如果你正在寻找并开始构建机器学习项目，那么这篇文章给你带来极大好处。

3类机器学习算法（广义上）

  1. 监督学习
    工作原理：该算法由一组目标/结果变量（或因变量）组成，该变量将根据给定的一组预测变量（独立变量）进行预测。 使用这些变量集，我们生成一个将输入映射到所需输出的函数。 训练过程继续进行执行，直到模型达到培训数据所需的准确度水平。 监督学习的例子：回归，决策树，随机森林，KNN，逻辑回归等

  2. 无监督学习
    如何工作：在这个算法中，我们没有任何目标或结果变量来预测/估计。 用于不同群体的群体聚类和用于不同群体的客户进行特定干预。 无监督学习的例子：Apriori算法，K-means。

  3. 加强学习：
    工作原理：使用这种算法，机器受到学习和训练，作出具体决定。 它以这种方式工作：机器暴露在一个环境中，它连续不断地使用试错。 该机器从过去的经验中学习，并尝试捕获最好的知识，以做出准确的业务决策。 加强学习示例：马尔可夫决策过程

常见机器学习算法

以下是常用机器学习算法的列表。 这些算法几乎可以应用于任何数据问题：

  • 线性回归
  • 逻辑回归
  • 决策树
  • SVM
  • 朴素贝叶斯
  • KNN
  • K-Means
  • 随机森林
  • 降维算法
  • Gradient Boost＆Adaboost

1.线性回归

它用于基于连续变量来估计实际价值（房屋成本，电话数量，总销售额等）。在这里，我们通过拟合最佳线来建立独立变量和因变量之间的关系。这个最佳拟合线被称为回归线，由线性方程Y = a * X + b表示。

理解线性回归的最好方法是回想童年的经历。比如，你要求五年级的孩子通过体重来从小到大排序班里的学生，而事先不告诉学生们的体重！你认为孩子会做什么？他/她很可能在身高和体格上分析人物的体重，并使用这些可视参数的组合进行排列。这是现实生活中的线性回归！孩子实际上已经弄清楚，身高和体格将有一个关系与体重相关联，看起来就像上面的等式。

在这个方程式中：

Y-因变量
a - 斜率
X - 自变量
b - 截距
这些系数a和b是基于最小化数据点和回归线之间的距离的平方差之和导出的。

看下面的例子。这里我们确定了线性方程y = 0.2811x + 13.9的最佳拟合线。现在使用这个方程，我们可以找到一个人（身高已知）的体重。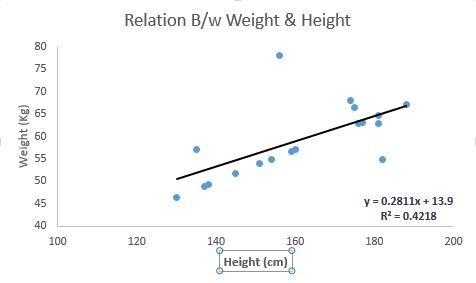
技术图片
线性回归主要有两种类型：简单线性回归和多元线性回归。 简单线性回归的特征在于一个自变量。 而且，多元线性回归（顾名思义）的特征是多个（多于1个）自变量。 在找到最佳拟合线的同时，可以拟合多项式或曲线回归线，这些被称为多项式或曲线回归。

Python Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#Import other necessary libraries like pandas, numpy...
from sklearn import linear_model
import numpy as np
#Load Train and Test datasets
#Identify feature and response variable(s) and values must be numeric and numpy arrays
# x_train=input_variables_values_training_datasets
x_train=np.random.rand(4,4)
print(x_train)
# y_train=target_variables_values_training_datasets
y_train=np.random.rand(4,4)
print(y_train)
# x_test=input_variables_values_test_datasets
x_test=np.random.rand(4,4)
print(x_test)
# Create linear regression object
linear = linear_model.LinearRegression()
# Train the model using the training sets and check score
linear.fit(x_train, y_train)
linear.score(x_train, y_train)
#Equation coefficient and Intercept
print('Coefficient: n', linear.coef_)
print('Intercept: n', linear.intercept_)
#Predict Output
predicted= linear.predict(x_test)
print('predicted:n',predicted)
[[ 0.98267731  0.23364069  0.35133775  0.92826309]
 [ 0.80538991  0.05637806  0.87662175  0.3960776 ]
 [ 0.54686738  0.6816495   0.99747716  0.32531085]
 [ 0.19189509  0.87105462  0.88158122  0.25056621]]
[[ 0.55541608  0.56859636  0.40616234  0.14683524]
 [ 0.09937835  0.63874553  0.92062536  0.32798326]
 [ 0.87174236  0.779044    0.79119392  0.06912842]
 [ 0.87907434  0.53175367  0.01371655  0.11414196]]
[[ 0.37568516  0.17267374  0.51647046  0.04774661]
 [ 0.38573914  0.85335136  0.11647555  0.0758696 ]
 [ 0.67559384  0.57535368  0.88579261  0.26278658]
 [ 0.13829782  0.28328756  0.51170484  0.04260013]]
Coefficient: 
 [[ 0.55158868  1.45901817  0.31224322  0.49538173]
 [ 0.6995448   0.40804135  0.59938423  0.09084578]
 [ 1.79010371  0.21674532  1.60972012 -0.046387  ]
 [-0.31562917 -0.53767439 -0.16141312 -0.2154683 ]]
Intercept: 
 [-0.89705102 -0.50908061 -1.9260686   0.83934127]
predicted:
 [[-0.25297601  0.13808785 -0.38696891  0.53426883]
 [ 0.63472658  0.18566989 -0.86662193  0.22361739]
 [ 0.72181277  0.75309881  0.82170796  0.11715048]
 [-0.22656611  0.01383581 -0.79537442  0.55159912]]

R Code

1
2
3
4
5
6
7
8
9
10
11
#Load Train and Test datasets
#Identify feature and response variable(s) and values must be numeric and numpy arrays
x_train <- input_variables_values_training_datasets
y_train <- target_variables_values_training_datasets
x_test <- input_variables_values_test_datasets
x <- cbind(x_train,y_train)
# Train the model using the training sets and check score
linear <- lm(y_train ~ ., data = x)
summary(linear)
#Predict Output
predicted= predict(linear,x_test)

2.逻辑回归

不要因为它的名字而感到困惑，逻辑回归是一个分类算法而不是回归算法。它用于基于给定的一组自变量来估计离散值（二进制值，如0/1，是/否，真/假）。简单来说，它通过将数据拟合到logit函数来预测事件发生的概率。因此，它也被称为logit回归。由于它预测概率，其输出值在0和1之间（如预期的那样）。

再次，让我们通过一个简单的例子来尝试理解这一点。

假设你的朋友给你一个难题解决。只有2个结果场景 - 你能解决和不能解决。现在想象，你正在被许多猜谜或者简单测验，来试图理解你擅长的科目。这项研究的结果将是这样的结果 - 如果给你一个10级的三角形问题，那么你有70％可能会解决这个问题。另外一个例子，如果是五级的历史问题，得到答案的概率只有30％。这就是逻辑回归为你提供的结果。

对数学而言，结果的对数几率被建模为预测变量的线性组合。

odds= p/ (1-p) = probability of event occurrence / probability of not event occurrence ln(odds) = ln(p/(1-p)) logit(p) = ln(p/(1-p)) = b0+b1X1+b2X2+b3X3....+bkXk

以上，p是感兴趣特征的概率。 它选择最大化观察样本值的可能性的参数，而不是最小化平方误差的总和（如在普通回归中）。

现在，你可能会问，为什么要采用log？ 为了简单起见，让我们来说，这是复制阶梯函数的最好的数学方法之一。 我可以进一步详细介绍，但这将会打破这篇文章的目的。
技术图片

Python Code

1
2
3
4
5
6
7
8
9
10
11
12
13
from sklearn.linear_model import LogisticRegression
#Assumed you have, X (predictor) and Y (target) for training data set and x_test(predictor) of test_dataset
# Create logistic regression object
model = LogisticRegression()
# Train the model using the training sets and check score
model.fit(X, y)
model.score(X, y)
#Equation coefficient and Intercept
print('Coefficient: n', model.coef_)
print('Intercept: n', model.intercept_)
#Predict Output
predicted= model.predict(x_test)

R Code

1
2
3
4
5
6
x <- cbind(x_train,y_train)
# Train the model using the training sets and check score
logistic <- glm(y_train ~ ., data = x,family='binomial')
summary(logistic)
#Predict Output
predicted= predict(logistic,x_test)

3.决策树

这是我最喜欢的算法之一，我经常使用它。 它是一种主要用于分类问题的监督学习算法，令人惊讶的是，它可以适用于分类和连·续因变量。 在该算法中，我们将群体分为两个或多个均匀集合。 这是基于最重要的属性/自变量来做出的并将它们分为不同的组。关于决策树的更多细节，你可以阅读决策树简介

技术图片
在上图中，您可以看到根据多个属性将群体分为四个不同的群组，以确定用户“是否可以玩”。为了 将人口分为不同的特征群体，它使用了诸如Gini，信息增益，卡方，熵等各种技术。
技术图片
了解决策树如何运作的最佳方法是播放Jezzball - 微软的经典游戏（下图）。 大体上就是，来一起在屏幕上滑动手指，筑起墙壁，掩住移动的球吧。

Python Code

1
2
3
4
5
6
7
8
9
10
11
12
13
#Import other necessary libraries like pandas, numpy...
from sklearn import tree
#Assumed you have, X (predictor) and Y (target) for training data set and x_test(predictor) of test_dataset
# Create tree object 
model = tree.DecisionTreeClassifier(criterion='gini') 
# for classification, here you can change the algorithm as gini or entropy (information gain) by default it is gini  
# model = tree.DecisionTreeRegressor() for regression
# Train the model using the training sets and check score
model.fit(X, y)
model.score(X, y)
#Predict Output
predicted= model.predict(x_test)

R Code

1
2
3
4
5
6
7
library(rpart)
x <- cbind(x_train,y_train)
# grow tree 
fit <- rpart(y_train ~ ., data = x,method="class")
summary(fit)
#Predict Output 
predicted= predict(fit,x_test)

4.SVM(支持向量机)

这是一种分类方法。 在这个算法中，我们将每个数据项目绘制为n维空间中的一个点（其中n是拥有的特征数），每个特征的值是特定坐标的值。

例如，如果我们有一个人的“高度”和“头发长度”这两个特征，我们首先将这两个变量绘制在二维空间中，其中每个点都有两个坐标（这些坐标称为支持向量）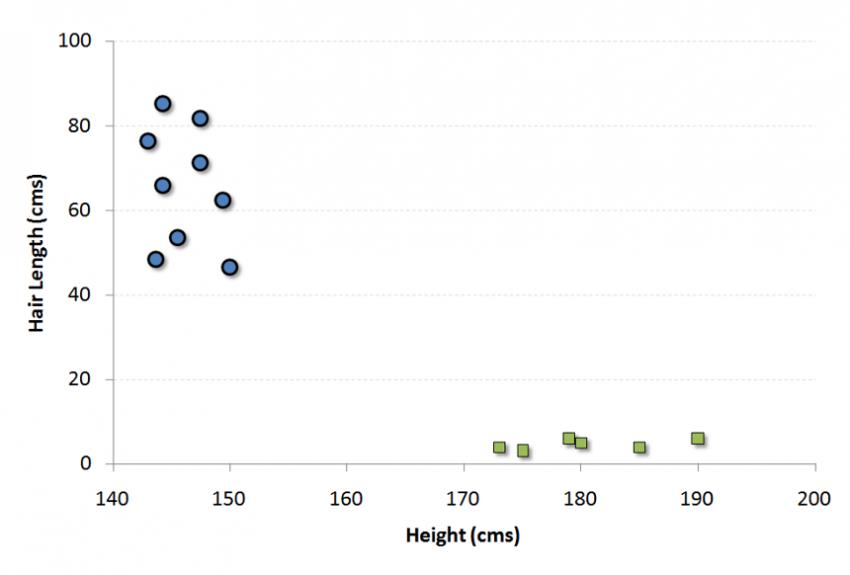
技术图片
现在，我们将找到一些可以将数据分割成两类的线。 而我们想要的线，就是使得两组数据中最近点到分割线的距离最长的线。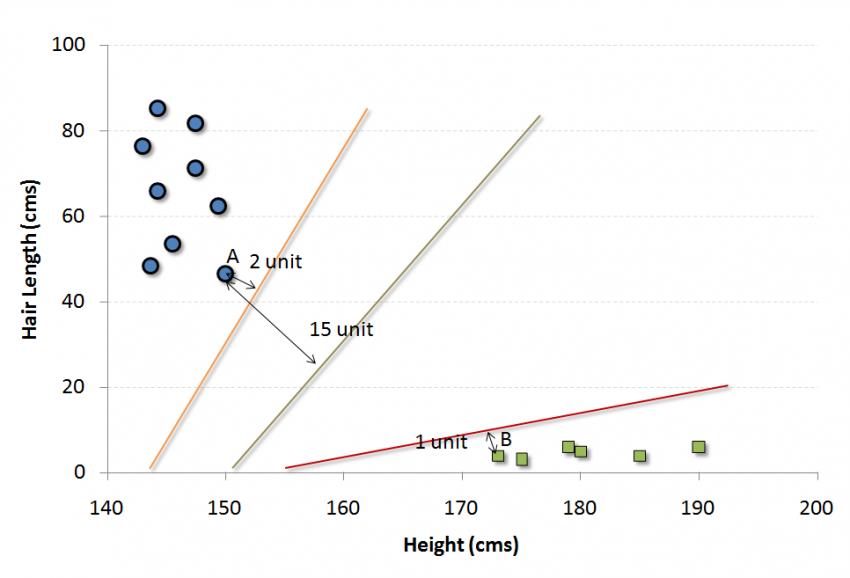
技术图片
在上述示例中，将数据分成两个不同分类的组的线是黑线，因为两个最接近的点距离线最远（红线也可以，但不是一最远）。 这条线是我们的分类器， 然后根据测试数据位于线路两边的位置，我们可以将新数据分类为什么类别。

Python Code

1
2
3
4
5
6
7
8
9
10
from sklearn import svm
#Assumed you have, X (predictor) and Y (target) for training data set and x_test(predictor) of test_dataset
# Create SVM classification object 
model = svm.svc() # there is various option associated with it, this is simple for classification. You can refer link, for mo# re detail.
# Train the model using the training sets and check score
model.fit(X, y)
model.sc 大专栏  机器学习算法的基本知识（使用Python和R代码）ore(X, y)
#Predict Output
predicted= model.predict(x_test)

R Code

1
2
3
4
5
6
7
library(e1071)
x <- cbind(x_train,y_train)
# Fitting model
fit <-svm(y_train ~ ., data = x)
summary(fit)
#Predict Output 
predicted= predict(fit,x_test)

5. 朴素贝叶斯

它是基于贝叶斯定理的分类技术，假设预测因子之间是独立的。 简单来说，朴素贝叶斯分类器假设类中特定特征的存在与任何其他特征的存在无关。 例如，如果果实是红色，圆形，直径约3英寸，则果实可能被认为是苹果。 即使这些特征依赖于彼此或其他特征的存在，一个朴素的贝叶斯分类器将考虑的是所有属性来单独地贡献这个果实是苹果的概率。

朴素贝叶斯模型易于构建，对于非常大的数据集尤其有用。 除了简单之外，朴素贝叶斯也被称为超高级分类方法。

贝叶斯定理提供了一种由P（c），P（x）和P（x | c）计算概率P（c | x）的方法。 看下面的等式：
技术图片

  • 其中：
    • P（c | x）是在x条件下c发生的概率。
    • P（c）是c发生的概率。
    • P（x | c）在c条件下x发生的概率。
    • P（x）是x发生的概率。

示例：

让我们用一个例子来理解它。 下面我有一个天气和相应的目标变量“玩游戏”的训练数据集。 现在，我们需要根据天气条件对玩家是否玩游戏进行分类。 我们按照以下步骤执行。

步骤1：将数据集转换为频率表

步骤2：通过发现像“Overcast”概率= 0.29和播放概率为0.64的概率来创建似然表。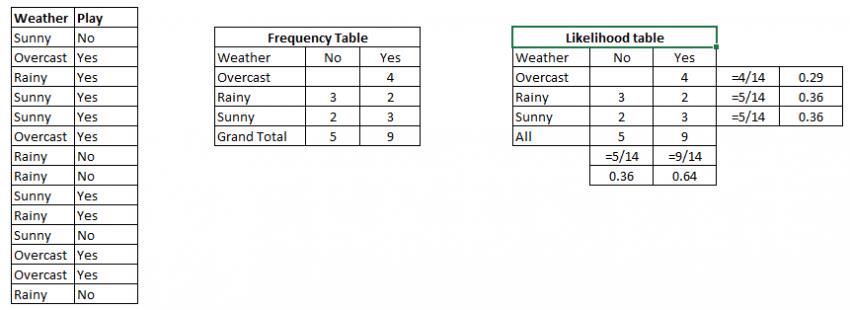
技术图片
步骤3：现在，使用朴素贝叶斯方程来计算每个类的概率。 其中概率最高的情况就是是预测的结果。

问题：

如果天气晴朗，玩家会玩游戏，这个说法是正确的吗？

我们可以使用上述方法解决，所以P(Yes | Sunny) = P( Sunny | Yes) * P(Yes) / P (Sunny)

这里，P（Sunny | Yes）= 3/9 = 0.33，P（Sunny）= 5/14 = 0.36，P（Yes）= 9/14 = 0.64

现在，P（Yes | Sunny）= 0.33 * 0.64 / 0.36 = 0.60，该事件发生的概率还是比较高的。

朴素贝叶斯使用类似的方法根据各种属性预测不同分类的概率，该算法主要用于文本分类和具有多个类的问题。

Python Code

1
2
3
4
5
6
7
8
9
from sklearn.naive_bayes import GaussianNB
#Assumed you have, X (predictor) and Y (target) for training data set and x_test(predictor) of test_dataset
# Create SVM classification object model = GaussianNB() 
# there is other distribution for multinomial classes like Bernoulli Naive Bayes, Refer link
# Train the model using the training sets and check score
model.fit(X, y)
#Predict Output
predicted= model.predict(x_test)

R Code

1
2
3
4
5
6
7
library(e1071)
x <- cbind(x_train,y_train)
# Fitting model
fit <-naiveBayes(y_train ~ ., data = x)
summary(fit)
#Predict Output 
predicted= predict(fit,x_test)

6. KNN (K-近邻算法)

它可以用于分类和回归问题, 然而，它在行业中被广泛地应用于分类问题。 K-近邻算法用于存储所有训练样本集（所有已知的案列），并通过其k个邻近数据多数投票对新的数据（或者案列）进行分类。通常，选择k个最近邻数据中出现次数最多的分类作为新数据的分类。

这些计算机的距离函数可以是欧几里德，曼哈顿，闵可夫斯基和汉明距离。 前三个函数用于连续函数，第四个函数用于分类变量。 如果K = 1，则简单地将该情况分配给其最近邻的类。 有时，选择K在执行KNN建模时是一个难点。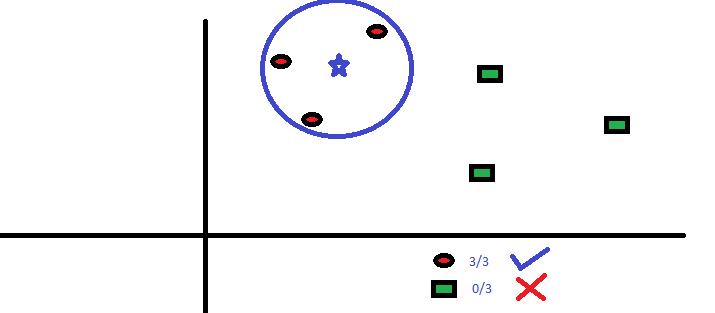
技术图片
KNN可以轻松映射到我们的现实生活中。 如果你想了解一个人，你没有任何信息，你可能想知道先去了解他的亲密的朋友和他活动的圈子，从而获得他/她的信息！

选择KNN之前要考虑的事项：

  • KNN在计算上是昂贵的
  • 变量应该被归一化，否则更高的范围变量可以偏移它
  • 在进行KNN之前，预处理阶段的工作更像去除离群值、噪声值

Python Code

1
2
3
4
5
6
7
8
9
from sklearn.neighbors import KNeighborsClassifier
#Assumed you have, X (predictor) and Y (target) for training data set and x_test(predictor) of test_dataset
# Create KNeighbors classifier object model 
KNeighborsClassifier(n_neighbors=6) # default value for n_neighbors is 5
# Train the model using the training sets and check score
model.fit(X, y)
#Predict Output
predicted= model.predict(x_test)

R Code

1
2
3
4
5
6
7
library(knn)
x <- cbind(x_train,y_train)
# Fitting model
fit <-knn(y_train ~ ., data = x,k=5)
summary(fit)
#Predict Output 
predicted= predict(fit,x_test)

7. K-Means

它是解决聚类问题的一种无监督算法。 其过程遵循一种简单而简单的方式，通过一定数量的聚类（假设k个聚类）对给定的数据集进行分类。 集群内的数据点与对等组是同构的和异构的。

尝试从油墨印迹中找出形状？（见下图） k means 与这个活动相似， 你通过墨水渍形状来判断有多少群体存在！
技术图片
下面两点感觉原文解释的不是很清楚，自己然后查了下国内的解释方法

K-means如何形成集群

  • （1） 从 n个数据对象任意选择 k 个对象作为初始聚类中心；
  • （2） 根据每个聚类对象的均值（中心对象），计算每个对象与这些中心对象的距离；并根据最小距离重新对相应对象进行划分；
  • （3） 重新计算每个（有变化）聚类的均值（中心对象）
  • （4） 循环（2）到（3）直到每个聚类不再发生变化为止参考

例子

技术图片
从上图中，我们可以看到，A，B，C，D，E是五个在图中点。而灰色的点是我们的种子点，也就是我们用来找点群的点。有两个种子点，所以K=2。

然后，K-Means的算法如下：

  1. 随机在图中取K（这里K=2）个种子点。
  2. 然后对图中的所有点求到这K个种子点的距离，假如点Pi离种子点Si最近，那么Pi属于Si点群。（上图中，我们可以看到A，B属于上面的种子点，C，D，E属于下面中部的种子点）
  3. 接下来，我们要移动种子点到属于他的“点群”的中心。（见图上的第三步）
  4. 然后重复第2）和第3）步，直到，种子点没有移动（我们可以看到图中的第四步上面的种子点聚合了A，B，C，下面的种子点聚合了D，E）。参考

K值如何确定

在实际应用中，由于Kmean一般作为数据预处理，或者用于辅助分聚类贴标签。所以k一般不会设置很大。可以通过枚举，令k从2到一个固定值如10，在每个k值上重复运行数次kmeans(避免局部最优解)，并计算当前k的平均轮廓系数，最后选取轮廓系数最大的值对应的k作为最终的集群数目。参考

我们知道随着群集数量的增加，该值不断减少，但是如果绘制结果，则可能会发现平方距离的总和急剧下降到k的某个值，然后再慢一些。 在这里，我们可以找到最佳聚类数。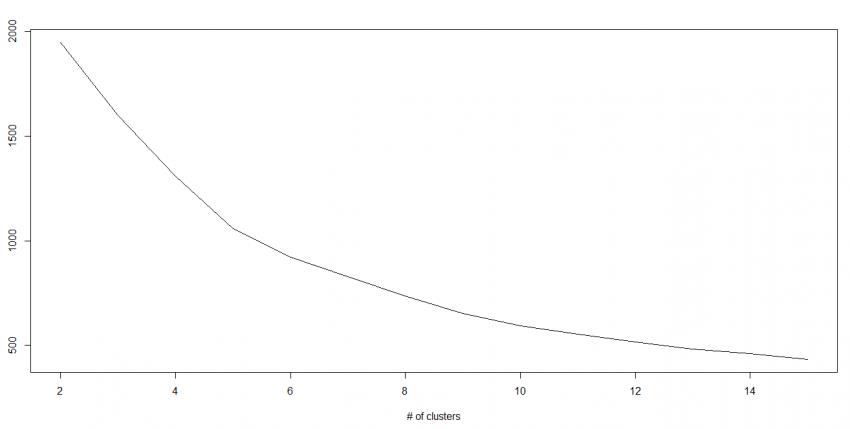
技术图片

Python Code

1
2
3
4
5
6
7
8
9
from sklearn.cluster import KMeans
#Assumed you have, X (attributes) for training data set and x_test(attributes) of test_dataset
# Create KNeighbors classifier object model 
k_means = KMeans(n_clusters=3, random_state=0)
# Train the model using the training sets and check score
model.fit(X)
#Predict Output
predicted= model.predict(x_test)

R Code

1
2
library(cluster)
fit <- kmeans(X, 3) # 5 cluster solution

8. Random Forest（随机树林）

随机森林(Random Forest)是一个包含多个决策树的分类器， 其输出的类别由个别树输出类别的众数而定。（相当于许多不同领域的专家对数据进行分类判断，然后投票）
技术图片
感觉原文没有将什么实质内容，给大家推进这一篇Random Forest入门

9. 降维算法

在过去的4-5年中，数据挖掘在每个可能的阶段都呈指数级增长。 公司/政府机构/研究机构不仅有新的来源，而且他们正在非常详细地挖掘数据。

例如：电子商务公司正在捕获更多关于客户的细节，例如人口统计，网络爬网历史，他们喜欢或不喜欢的内容，购买历史记录，反馈信息等等，给予他们个性化的关注，而不是离你最近的杂货店主。

作为数据科学家，我们提供的数据还包括许多功能，这对建立良好的稳健模型是非常有用的，但是有一个挑战。 你如何识别出1000或2000年高度重要的变量？ 在这种情况下，维数降低算法可以帮助我们与决策树，随机森林，PCA，因子分析，基于相关矩阵，缺失值比等的其他算法一起使用。
要了解更多有关此算法的信息，您可以阅读 “Beginners Guide To Learn Dimension Reduction Techniques“.

Python Code

1
2
3
4
5
6
7
8
9
10
from sklearn import decomposition
#Assumed you have training and test data set as train and test
# Create PCA obeject pca= decomposition.PCA(n_components=k) #default value of k =min(n_sample, n_features)
# For Factor analysis
#fa= decomposition.FactorAnalysis()
# Reduced the dimension of training dataset using PCA
train_reduced = pca.fit_transform(train)
#Reduced the dimension of test dataset
test_reduced = pca.transform(test)

For more detail on this, please refer this link.

R Code

1
2
3
4
library(stats)
pca <- princomp(train, cor = TRUE)
train_reduced  <- predict(pca,train)
test_reduced  <- predict(pca,test)

10. Gradient Boosting & AdaBoost

当我们处理大量数据以预测高预测能力时，GBM＆AdaBoost是更加强大的算法。 Boosting是一种综合学习算法，它结合了几个基本估计器的预测，以提高单个估计器的鲁棒性。 它将多个弱或平均预测值组合到一个强大的预测变量上。 这些提升算法在数据科学比赛中总是能够很好地运行，如Kaggle，AV Hackathon，CrowdAnalytix。
More: Know about Gradient and AdaBoost in detail

Python Code

1
2
3
4
5
6
7
8
9
from sklearn.ensemble import GradientBoostingClassifier
#Assumed you have, X (predictor) and Y (target) for training data set and x_test(predictor) of test_dataset
# Create Gradient Boosting Classifier object
model= GradientBoostingClassifier(n_estimators=100, learning_rate=1.0, max_depth=1, random_state=0)
# Train the model using the training sets and check score
model.fit(X, y)
#Predict Output
predicted= model.predict(x_test)

R Code

1
2
3
4
5
6
library(caret)
x <- cbind(x_train,y_train)
# Fitting model
fitControl <- trainControl( method = "repeatedcv", number = 4, repeats = 4)
fit <- train(y ~ ., data = x, method = "gbm", trControl = fitControl,verbose = FALSE)
predicted= predict(fit,x_test,type= "prob")[,2]

结束语

现在我相信，你会有一个常用的机器学习算法的想法。 我在写这篇文章和提供R和Python中的代码的唯一意图就是让你马上开始。 如果您想要掌握机器学习，请将算法运用实际问题，体会其中的乐趣

以上是关于机器学习算法的基本知识（使用Python和R代码）的主要内容，如果未能解决你的问题，请参考以下文章

建模分析之机器学习算法（附python&R代码）

译文：朴素贝叶斯算法简介（Python和R中的代码）

机器学习实验scikit-learn的主要模块和基本使用

机器学习算法基础（Python和R语言实现）

机器学习加深度学习资料大放送（附上资料群）

机器学习模型和算法