EulerNet Adaptive Feature Interaction Learning via Euler’s Formula for CTR Prediction

Posted 2023-06-19 馒头and花卷

目录

• 概
• Motivation
• Eulernet
  • Explict
  • Implict
• 优化
• 代码

Tian Z., Bai T., Zhao W., Wen J. and Cao Z. Eulernet: Adaptive feature interaction learning via euler’s formula for ctr prediction. SIGIR, 2023.

概

一种能够自适应地学习阶数地网络.

Motivation

• 高阶信息, 对于 CTR 任务而言是十分重要的, 之前的方法, 通常需要我们显式地构造这种信息:

  \\[\\Delta_ex = \\sum_\\alpha \\in \\mathcalA \\bme_1^\\alpha_1 \\odot \\bme_2^\\alpha_2 \\odot \\cdots \\odot \\bme_m^\\alpha_m, \\]

  其中 \\(\\bm\\alpha = [\\alpha_1, \\alpha_2, \\ldots, \\alpha_m]\\) 是不同的阶数.

• 为了充分利用高阶信息, 我们可能需要合理地设计 \\(\\mathcalA\\), 而这通常是困难的. 我们需要一种能够自适应的学习方式来处理.

Eulernet

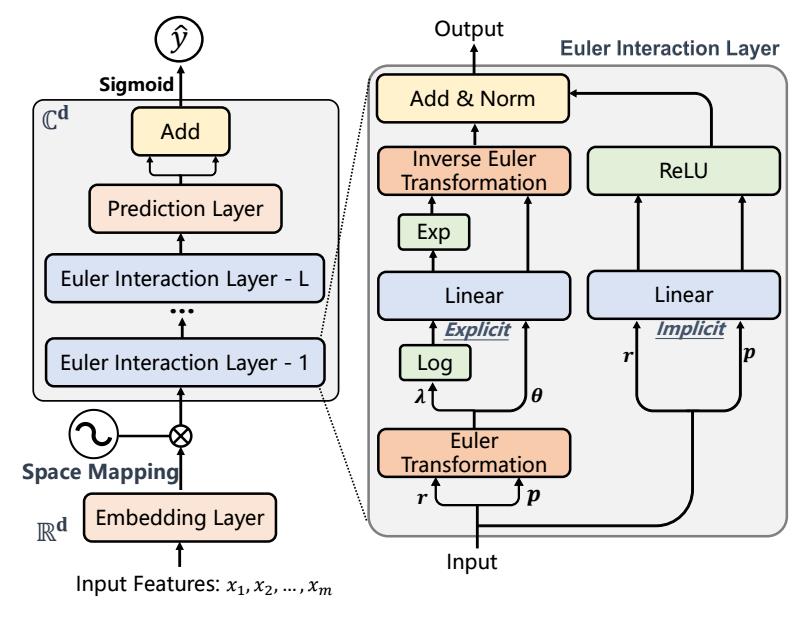
• Eulernet 主要是 Euler Interaction Layer 的设计.

Explict

• 每一层的输入为:

  \\[\\bmr_j + i \\bmp_j \\]

  对于最初输入, \\(\\bmr_j = \\mu_j \\cos(\\bme_j), \\quad \\bmp_j = \\mu_j \\sin (\\bme_j)\\), 其中 \\(\\mu_j\\) 亦为可学习的参数.

• 我们知道, 对于

  \\[\\tilde\\bme_j = \\bmr_j + i \\bmp_j = \\bm\\lambda_j e^i \\bm\\theta_j, \\]

  其中 (我们可以通过极坐标变换得到)

  \\[\\bm\\lambda_j = \\sqrt\\bmr_j^2 + \\bmp_j^2, \\bm\\theta_j = \\textatan2(\\bmp_j, \\bmr_j), \\]

  atan2 是反三角函数.

• 我们希望得到高阶信息 (先考虑一个 \\(\\alpha\\)):

  \\[\\Delta_ex = \\tilde\\bme_1^\\alpha_1 \\odot \\tilde\\bme_2^\\alpha_2 \\odot \\cdots \\odot \\tilde\\bme_m^\\alpha_m, \\]

  可以发现:

  \\[\\beginarrayll \\Delta_ex &= \\tilde\\bme_1^\\alpha_1 \\odot \\tilde\\bme_2^\\alpha_2 \\odot \\cdots \\odot \\tilde\\bme_m^\\alpha_m \\\\ &= \\prod_j=1^m (\\bm\\lambda_j^\\alpha_j \\exp(i \\alpha_j \\bm\\theta_j)) \\\\ &= \\exp(\\sum_j=1^m \\alpha_j \\log (\\bm\\lambda_j)) \\exp(i \\sum_j=1^m\\alpha_j \\bm\\theta_j)). \\\\ \\endarray \\]

  如此一来乘法就全部变成加法了 (好处?)

• 若令

  \\[\\bm\\psi_k = \\sum_j=1^m \\alpha_k, j \\bm\\theta_j + \\bm\\delta_k, \\\\ \\bml_k = \\exp(\\sum_j=1^m \\alpha_k, j \\log (\\bm\\lambda_j) + \\bm\\delta_k\'), \\]

  则更一般的高阶信息可以用如下方式表示:

  \\[\\Delta_ex = \\bml_k e^i \\bm\\psi_k. \\]

• 得到 \\(\\Delta_ex\\) 之后, 为了下一层的继续进行, 我们需要拆解出实部和虚部:

  \\[\\hat\\bmr_k = \\bml_k \\cos(\\bm\\psi_k), \\\\ \\hat\\bmp_k = \\bml_k \\sin(\\bm\\psi_k). \\\\ \\]

• 如果有更多的高阶信息需要建模, 可以:

  \\[\\Delta_ex = \\sum_k=1^n (\\hat\\bmr_k + i \\hat\\bmp_k). \\]

Implict

• 此外, Eulernet 还有 implict 的信息建模部分:

  \\[\\bmr_k\' = \\textReLU(\\mathbfW_k \\bmr + \\bmb_k), \\\\ \\bmp_k\' = \\textReLU(\\mathbfW_k \\bmp + \\bmb_k). \\\\ \\]

• 两部分信息, 相加并通过 normlization layer 归一化.

优化

• 假设最后的输出为:

  \\[\\\\tilde\\bmr_k + i \\tilde\\bmp_k\\_k=1^n, \\]

  通过如下方式进行回归预测:

  \\[\\haty = \\sigma(z_re + z_im), \\\\ z = \\mathbfw^T \\tilde\\bmr + i (\\mathbfw^T \\tilde\\bmp) = z_re + iz_im, \\\\ \\tilde\\bmr = [\\tilde\\bmr_1, \\tilde\\bmr_2, \\ldots, \\tilde\\bmr_n] \\in \\mathbbR^nd \\\\ \\tilde\\bmp = [\\tilde\\bmp_1, \\tilde\\bmp_2, \\ldots, \\tilde\\bmp_n] \\in \\mathbbR^nd. \\\\ \\]

• 然后通过 BCE 进行优化.

代码

[official]