R语言中的隐马尔可夫HMM模型实例|附代码数据
Posted 大数据部落
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了R语言中的隐马尔可夫HMM模型实例|附代码数据相关的知识,希望对你有一定的参考价值。
原文链接:http://tecdat.cn/?p=17592
最近我们被客户要求撰写关于隐马尔可夫HMM模型的研究报告,包括一些图形和统计输出。
最近,我们使用隐马尔可夫模型开发了一种解决方案,并被要求解释这个方案
HMM用于建模数据序列,无论是从连续概率分布还是从离散概率分布得出的。它们与状态空间和高斯混合模型相关,因为它们旨在估计引起观测的状态。状态是未知或“隐藏”的,并且HMM试图估计状态,类似于无监督聚类过程。
例子
在介绍HMM背后的基本理论之前,这里有一个示例,它将帮助您理解核心概念。有两个骰子和一罐软糖。B掷骰子,如果总数大于4,他会拿几颗软糖再掷一次。如果总数等于2,则他拿几把软糖,然后将骰子交给A。现在该轮到A掷骰子了。如果她的掷骰大于4,她会吃一些软糖,但是她不喜欢黑色的其他颜色(两极分化的看法),因此我们希望B会比A多。他们这样做直到罐子空了。
现在假设A和B在不同的房间里,我们看不到谁在掷骰子。取而代之的是,我们只知道后来吃了多少软糖。我们不知道颜色,仅是从罐子中取出的软糖的最终数量。我们怎么知道谁掷骰子?HMM。
在此示例中,状态是掷骰子的人,A或B。观察结果是该回合中吃了多少软糖。如果该值小于4,骰子的掷骰和通过骰子的条件就是转移概率。由于我们组成了这个示例,我们可以准确地计算出转移概率,即1/12。没有条件说转移概率必须相同,例如A掷骰子2时可以将骰子移交给他,例如,概率为1/36。
模拟
首先,我们将模拟该示例。B平均要吃12颗软糖,而A则需要4颗。
# 设置
simulate <- function(N, dice.val = 6, jbns, switch.val = 4)
#模拟变量
#可以只使用一个骰子样本
#不同的机制,例如只丢1个骰子,或任何其他概率分布
b<- sample(1:dice.val, N, replace = T) + sample(1:dice.val, N, replace = T)
a <- sample(1:dice.val, N, replace = T) + sample(1:dice.val, N, replace = T)
bob.jbns <- rpois(N, jbns[1])
alice.jbns <- rpois(N, jbns[2])
# 状态
draws <- data.frame(state = rep(NA, N), obs = rep(NA, N),
# 返回结果
return(cbind(roll = 1:N, draws))
# 模拟场景
draws <- simulate(N, jbns = c(12, 4), switch.val = 4)
# 观察结果
ggplot(draws, aes(x = roll, y = obs)) + geom_line()
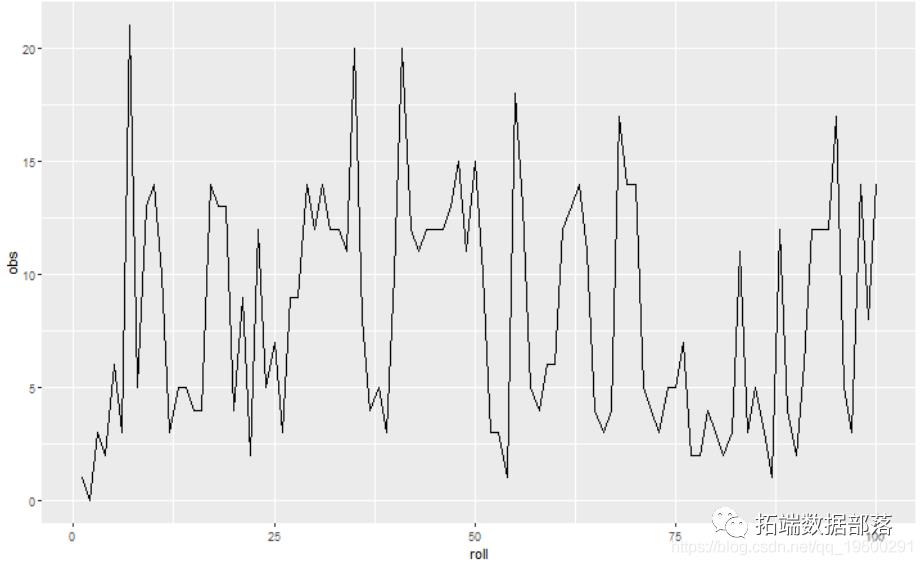
如您所见,仅检查一系列计数来确定谁掷骰子是困难的。我们将拟合HMM。由于我们正在处理计数数据,因此观察值是从泊松分布中得出的。
fit.hmm <- function(draws)
# HMM
mod <- fit(obs ~ 1, data = draws, nstates = 2, family = poisson()
# 通过估计后验来预测状态
est.states <- posterior(fit.mod)
head(est.states)
# 结果
hmm.post.df <- melt(est.states, measure.vars =
# 输出表格
print(table(draws[,c("state", "est.state.labels")]))
## iteration 0 logLik: -346.2084
## iteration 5 logLik: -274.2033
## converged at iteration 7 with logLik: -274.2033
## est.state.labels
## state alice bob
## a 49 2
## b 3 46
模型迅速收敛。使用后验概率,我们估计过程处于哪个状态,即谁拥有骰子,A或B。要具体回答该问题,我们需要更多地了解该过程。在这种情况下,我们知道A只喜欢黑软糖。否则,我们只能说该过程处于状态1或2。下图显示了HMM很好地拟合了数据并估计了隐藏状态。
# 绘图输出
g0 <- (ggplot(model.output$draws, aes(x = roll, y = obs)) + geom_line() +
theme(axis.ticks = element_blank(), axis.title.y = element_blank())) %>% ggplotGrob
g1 <- (ggplot(model.output$draws, aes(x = roll, y = state, fill = state, col = state)) +
g0$widths <- g1$widths
return(grid.arrange(g0, g1
plot.hmm.output(hmm1)

令人印象深刻的是,该模型拟合数据和滤除噪声以估计状态的良好程度。公平地说,可以通过忽略时间分量并使用EM算法来估计状态。但是,由于我们知道数据形成一个序列,因为观察下一次发生的概率取决于前一个即\\(P(X_t | X_ t-1)\\),其中\\(X_t \\ )是软糖的数量。
点击标题查阅往期内容

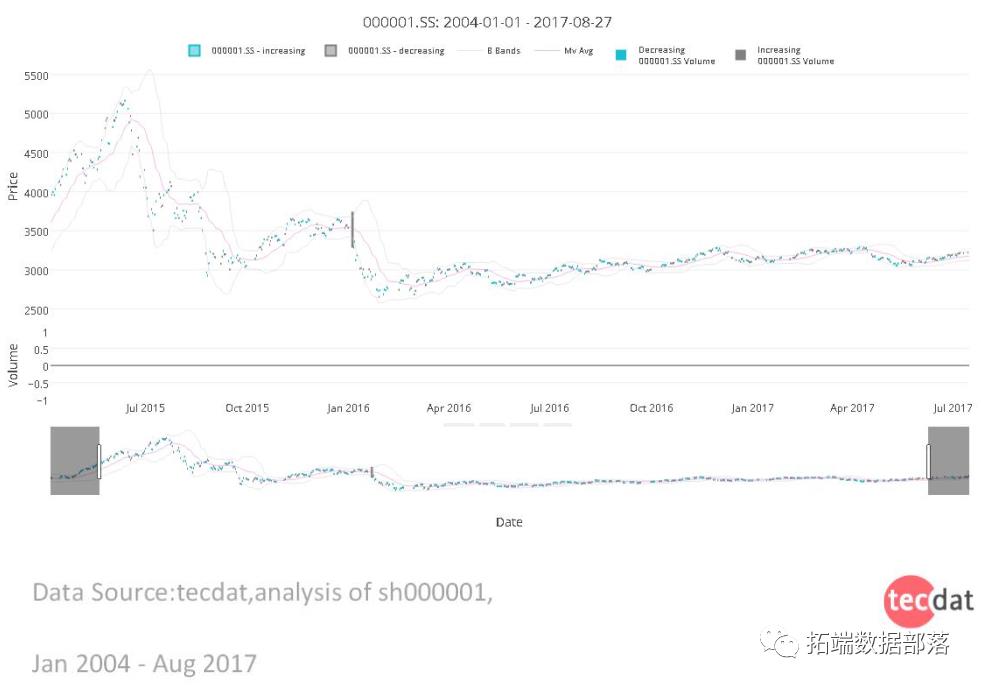
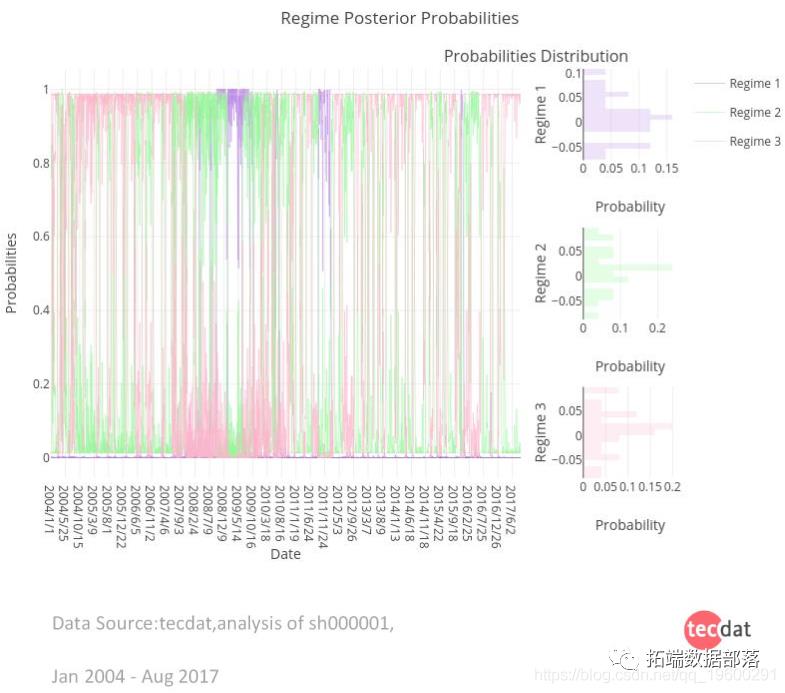
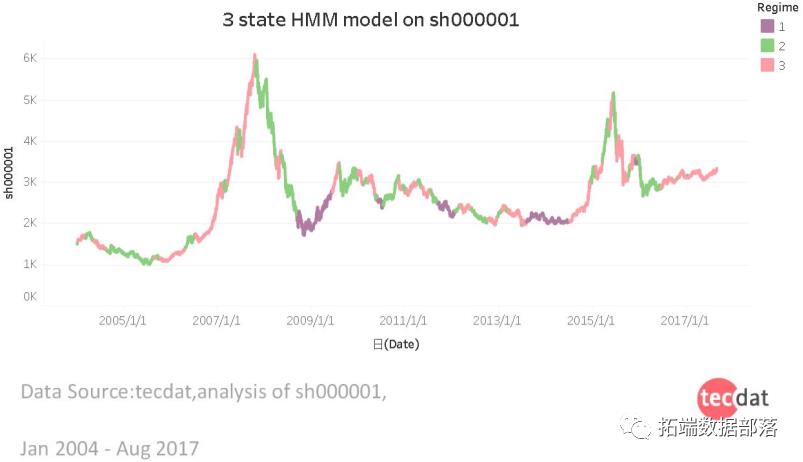
隐马尔可夫模型(HMM)识别不断变化的股市状况股票指数预测实战

左右滑动查看更多

01
02

03
04
考虑到我们构造的问题,这可能是一个相对简单的案例。如果转移概率大得多怎么办?
simulate(100, jbns = c(12, 4), switch.val = 7)
## iteration 0 logLik: -354.2707
## iteration 5 logLik: -282.4679
## iteration 10 logLik: -282.3879
## iteration 15 logLik: -282.3764
## iteration 20 logLik: -282.3748
## iteration 25 logLik: -282.3745
## converged at iteration 30 with logLik: -282.3745
## est.state.labels
## state alice bob
## alice 54 2
## bob 5 39
plot(hmm2)
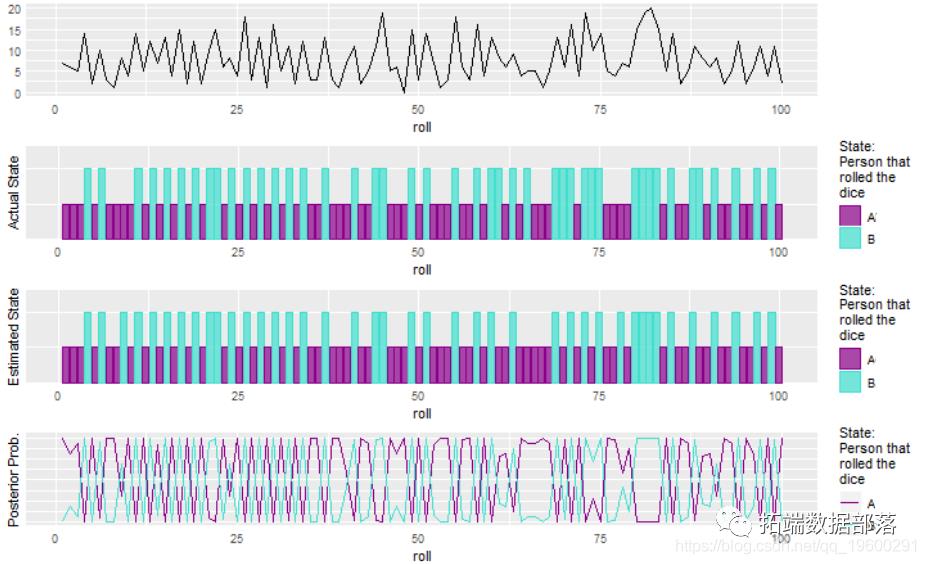 这有很多噪音数据,但是HMM仍然做得很好。性能的提高部分归因于我们对从罐中取出的软糖数量的选择。分布越明显,模型就越容易拾取转移。公平地讲,我们可以计算中位数,并将所有低于中位数的值都归为一个状态,而将所有高于中位数的值归为另一状态,您可以从结果中看到它们做得很好。这是因为转移概率非常高,并且预计我们会从每个状态观察到相似数量的观察结果。当转移概率不同时,我们会看到HMM表现更好。
这有很多噪音数据,但是HMM仍然做得很好。性能的提高部分归因于我们对从罐中取出的软糖数量的选择。分布越明显,模型就越容易拾取转移。公平地讲,我们可以计算中位数,并将所有低于中位数的值都归为一个状态,而将所有高于中位数的值归为另一状态,您可以从结果中看到它们做得很好。这是因为转移概率非常高,并且预计我们会从每个状态观察到相似数量的观察结果。当转移概率不同时,我们会看到HMM表现更好。
如果观察结果来自相同的分布,即A和B吃了相同数量的软糖怎么办?
hmm3 <- fit.hmm(draws)
plot(hmm3)
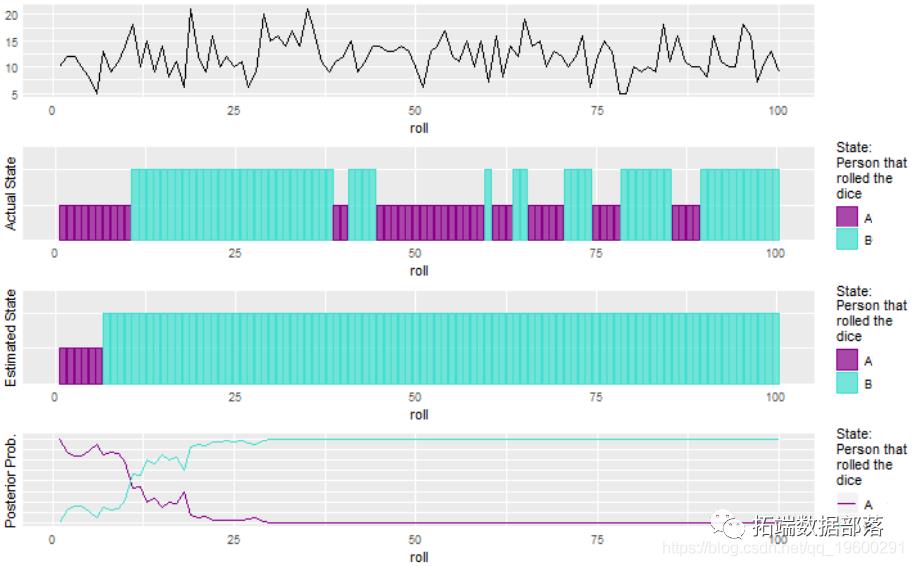 不太好,但这是可以预期的。如果从中得出观察结果的分布之间没有差异,则可能也只有1个状态。
不太好,但这是可以预期的。如果从中得出观察结果的分布之间没有差异,则可能也只有1个状态。
实际如何估算状态?
首先,状态数量及其分布方式本质上是未知的。利用对系统建模的知识,用户可以选择合理数量的状态。在我们的示例中,我们知道有两种状态使事情变得容易。可能知道确切的状态数,但这并不常见。再次通过系统知识来假设观察结果通常是合理的,这通常是合理的。
从这里开始,使用 Baum-Welch算法 来估计参数,这是EM算法的一种变体,它利用了观测序列和Markov属性。除了估计状态的参数外,还需要估计转移概率。Baum-Welch算法首先对数据进行正向传递,然后进行反向传递。然后更新状态转移概率。然后重复此过程,直到收敛为止。
在现实世界
在现实世界中,HMM通常用于
- 股票市场预测,无论市场处于牛市还是熊市
- 估计NLP中的词性
- 生物测序
- 序列分类
仅举几例。只要有观察序列,就可以使用HMM,这对于离散情况也适用。

点击文末 “阅读原文”
获取全文完整资料。
本文选自《R语言中的隐马尔可夫HMM模型实例》。
点击标题查阅往期内容
python中使用马尔可夫决策过程(MDP)动态编程来解决最短路径强化学习问题
隐马尔可夫模型(HMM)识别不断变化的股市状况股票指数预测实战
马尔可夫Markov区制转移模型分析基金利率
马尔可夫区制转移模型Markov regime switching
时变马尔可夫区制转换MRS自回归模型分析经济时间序列
马尔可夫转换模型研究交通伤亡人数事故时间序列预测
如何实现马尔可夫链蒙特卡罗MCMC模型、Metropolis算法?
Matlab用BUGS马尔可夫区制转换Markov switching随机波动率模型、序列蒙特卡罗SMC、M H采样分析时间序列
R语言BUGS序列蒙特卡罗SMC、马尔可夫转换随机波动率SV模型、粒子滤波、Metropolis Hasting采样时间序列分析
matlab用马尔可夫链蒙特卡罗 (MCMC) 的Logistic逻辑回归模型分析汽车实验数据
stata马尔可夫Markov区制转移模型分析基金利率
PYTHON用时变马尔可夫区制转换(MRS)自回归模型分析经济时间序列
R语言使用马尔可夫链对营销中的渠道归因建模
matlab实现MCMC的马尔可夫转换ARMA - GARCH模型估计
R语言隐马尔可夫模型HMM识别不断变化的股票市场条件
R语言中的隐马尔可夫HMM模型实例
用机器学习识别不断变化的股市状况—隐马尔科夫模型(HMM)
Matlab马尔可夫链蒙特卡罗法(MCMC)估计随机波动率(SV,Stochastic Volatility) 模型
MATLAB中的马尔可夫区制转移(Markov regime switching)模型
Matlab马尔可夫区制转换动态回归模型估计GDP增长率
R语言马尔可夫区制转移模型Markov regime switching
stata马尔可夫Markov区制转移模型分析基金利率
R语言如何做马尔可夫转换模型markov switching model
R语言隐马尔可夫模型HMM识别股市变化分析报告
R语言中实现马尔可夫链蒙特卡罗MCMC模型
隐马尔可夫(HMM)模型
隐马尔可夫(HMM)模型
隐马尔可夫模型,是一种概率图模型,一种著名的有向图模型,一种判别式模型。主要用于时许数据建模,在语音识别、自然语言处理等领域广泛应用。
概率图模型分为两类,一类:使用有向无环图表示变量间的依赖关系,称为有向图模型或者贝叶斯网;第二类:使用无向图表示变量间的依赖关系,称为无向图模型或者马尔可夫网。
判别式模型:考虑条件分布P(Y, R | O),生成式模型:考虑联合分布P(Y, R, O)
HMM三个假设
- 当前观测值只由当前隐藏状态决定
- 当前隐藏状态由前一个隐藏状态决定
- 隐藏状态之间转移概率不随时间改变
随机过程中某一时刻的状态st的概率分布为:
p(st|st-1,st-2,...,s0)=p(st|st-1)
即:t 时刻的状态仅依赖于 t-1 时刻的状态,与其余状态无关,这就是所谓的“马尔可夫链”
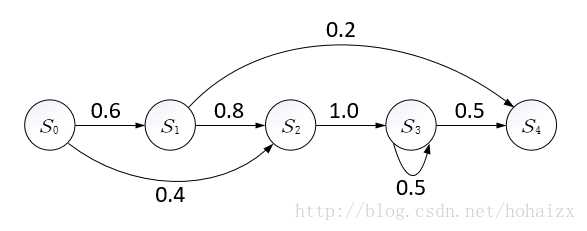
在马尔可夫链中,每一圆圈代表相应时刻的状态,有向边代表可能的状态转移,权重表示状态转移的概率
HMM模型结构图
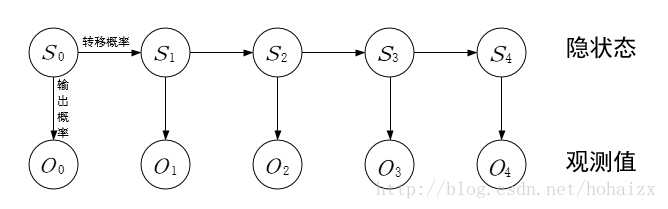
HMM模型五元组
HMM模型可以用五元组(O, S, A, B, π)表示。其中
- O: {o0, o1, ..., on} 表示观测系列,是系统的外在可观测变量。
- S: {s0, s1, ..., sn} 表示隐状态序列,是导致系统外在表现变化的内因。
- A: {aij = p(sj | si)} 表示状态转移概率。
- B: {bij = p(oj | si)} 表示输出概率,又称发射概率
- π: {π0, π1, ..., πm} 表示初始状态概率。
HMM三类问题
根据以上HMM模型五元组表示,我们可以归纳出HMM模型解决的三类主要问题。
一、评估问题
已知:状态转移矩阵 A, 初始状态概率 π,输出矩阵 B,观测序列
求:求该观测序列的可能性
解决算法:向前(forward)算法或者向后(backward)算法
二、解码问题
已知:状态转移矩阵A,初始状态概率 π,输出矩阵B,观测序列
求:最有可能产生该观测序列的隐藏状态序列
解决算法:维特比(Viterbi)算法,一种动态规划算法
三、学习问题
已知:很多观测序列
求:估计HMM模型参数的可能取值
解决算法:鲍姆韦尔奇(Baum-Welch)算法
以上是关于R语言中的隐马尔可夫HMM模型实例|附代码数据的主要内容,如果未能解决你的问题,请参考以下文章