数学公式：点到直线的距离

Posted 2023-06-11 快乐在角落里

求点到直线的距离，点 P(a,b)，直线 l 为 Ax + By + C = 0

过 P 点作垂直于 l 的直线 m

\\[l的点斜式为\\\\ y = -\\fracABx - \\fracCB\\\\ x = -\\fracBAy - \\fracCA\\\\ 求垂直斜率，通过斜率相乘得-1求得。k = \\fracBA\\\\ 则 m 的点斜式方程为\\\\ y = \\fracBA(x-a) + b\\\\ 一般式为\\\\ Ay = B(x-a)+Ab\\\\ Ay = Bx-Ba+Ab\\\\ -Bx=-Ay-Ba+Ab\\\\ Bx=Ay+Ba-Ab\\\\ x的式子为\\\\ x=\\fracABy+a - \\fracAbB \\]

通过两个方程计算交点 Q 的坐标

求 x

\\[-\\fracABx-\\fracCB = \\fracBAx-\\fracBaA+b\\\\ -\\fracAABBx-\\fracABCB = \\fracABBAx-\\fracABBaA+ABb \\\\ -A^2x-AC = B^2x-B^2a+ABb\\\\ -B^2x - A^2x = -B^2a+ABb +AC\\\\ A^2x + B^2x = B^2a-ABb - AC\\\\ (A^2+B^2)x = B^2a-ABb - AC\\\\ x = \\fracB^2a-ABb - ACA^2+B^2 \\]

求 y

\\[-\\fracBAy - \\fracCA = \\fracABy+a - \\fracAbB\\\\ -\\fracABBAy - \\fracABCA = \\fracABABy+ABa - \\fracABAbB\\\\ -B^2y - BC = A^2y + ABa - A^2b \\\\ -BC-ABa+A^2b = (A^2+B^2)y\\\\ y=\\fracA^2b-ABa-BCA^2+B^2 \\]

则点 Q坐标为

\\[(\\fracB^2a-ABb - ACA^2+B^2,\\fracA^2b-ABa-BCA^2+B^2) \\]

先求出了垂直线的方程，再求出了两直线的交点坐标，因此可以通过两点间距离公式算出点到直线的距离

\\[\\beginalign |PQ| &= \\sqrt(x-a)^2+(y-b)^2\\\\ &=\\sqrt(\\fracB^2a-ABb - ACA^2+B^2-a)^2+(\\fracA^b-ABa-BCA^2+B^2-b)^2\\\\ &=\\sqrt(\\fracB^2a-ABb - AC-a(A^2+B^2)A^2+B^2)^2+(\\fracA^2b-ABa-BC-b(A^2+B^2)A^2+B^2)^2\\\\ &=\\sqrt(\\fracB^2a-ABb - AC-A^2a-B^2aA^2+B^2)^2+(\\fracA^2b-ABa-BC-A^2b-B^2bA^2+B^2)^2\\\\ &=\\sqrt(\\frac-ABb - AC-A^2aA^2+B^2)^2+(\\frac-ABa-BC-B^2bA^2+B^2)^2\\\\ &=\\sqrt(\\fracA(-Bb - C-Aa)A^2+B^2)^2+(\\fracB(-Aa-C-Bb)A^2+B^2)^2\\\\ &=\\sqrt(\\fracA^2(-Bb - C-Aa)^2(A^2+B^2)^2)+(\\fracB^2(-Aa-C-Bb)^2(A^2+B^2)^2)\\\\ &=\\sqrt(\\fracA^2(-Bb - C-Aa)^2+B^2(-Aa-C-Bb)^2(A^2+B^2)^2)\\\\ &=\\sqrt(\\fracA^2(-Aa-Bb-C)^2+B^2(-Aa-Bb-C)^2(A^2+B^2)^2)\\\\ &=\\sqrt(\\frac(A^2+B^2)(-Aa-Bb-C)^2)(A^2+B^2)^2)\\\\ &=\\sqrt(\\frac(-Aa-Bb-C)^2A^2+B^2)\\\\ &=\\frac\\left| -(-Aa-Bb-C) \\right|\\sqrtA^2+B^2\\\\ &=\\frac\\left| Aa+Bb+C \\right|\\sqrtA^2+B^2 \\endalign \\]

算是推出来了吧，难受的很，好几次都因为前面算错了导致最后这部算不出来，浪费了很多时间

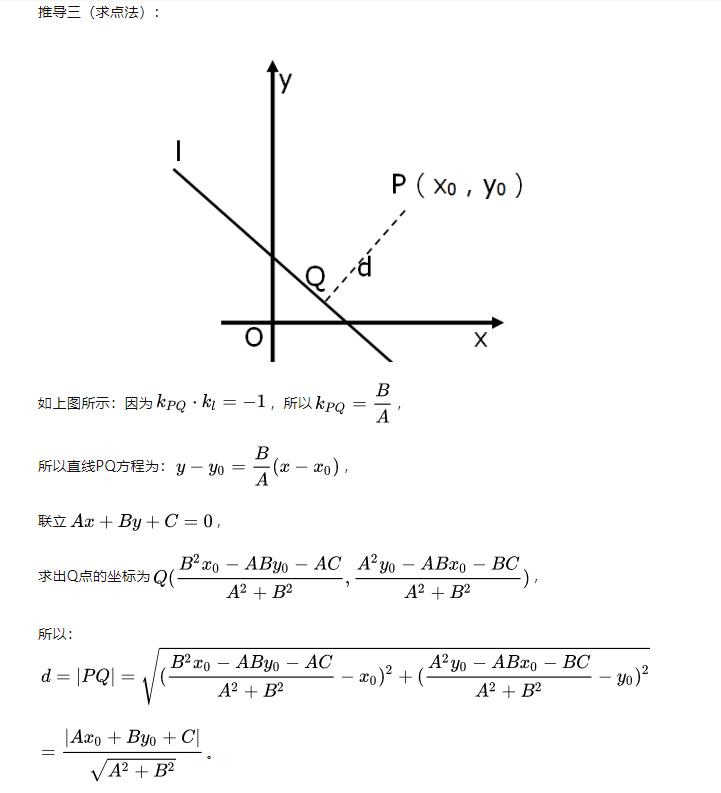
点到直线距离公式的几种推导