11

Posted 2023-06-10 zhouyi207

I would like to introduce an article titled "The Most Dangerous Equation" by Howard Wainer. Howard Wainer is an American statistician and data visualization expert, who is an honorary professor at New York University, and has served as a senior researcher at Bell Labs and chief scientist at IBM. The article "The Most Dangerous Equation" by Howard Wainer is a thought-provoking discussion of the potential dangers of misunderstanding or misusing some statistical equations related to the law of large numbers. The author uses four historical examples from different fields to illustrate how ignorance or arrogance of statistics can lead to serious consequences. The author\'s purpose is to inform and educate readers about the importance of understanding the limitations and potential misuse of mathematical equations, and to promote more accurate analysis and decision making in various domains.

In this article, he first defines what a dangerous equation is: "Some equations are dangerous if you know them, and others are dangerous if you do not." Then he introduces the topic of the article through the mass-energy equation, which we all know can be used to make atomic bombs with terrifying destructive power. However, the topic of this article is not physics, but statistics. I believe have all heard of a story in India that there is an ancient legend: King Shah wanted to reward the inventor of chess - the prime minister: Sissa bin Dahir. The king asked him what he wanted, and he said to the king: "Your Majesty, please reward me with one grain of wheat in the first small square on this chessboard, two grains in the second small square, four grains in the third small square, and so on. Please reward your servant with all the grains of wheat that fill all 64 squares on the chessboard!" The king thought this request was too easy to satisfy, so he ordered him to give him these grains of wheat. When people brought bags of wheat and started counting, the king realized that even if all the wheat in India or even the world was brought over, it would not satisfy the prime minister\'s request. Through this story we can see that ignorance and arrogance of mathematics or statistics can bring some very serious dangers. This article tells four such similar stories around the law of large numbers. Each story is very representative:

The first one is "Pyx Trial", which is a trial about coin standards and quality. In 1150, the British king realized that the value of coins should be based on their precious metal content, rather than simply being priced by the king. They set a standard for coin gold content, such as a "guinea" coin should weigh 128 grains. They also set an upper limit for coin weight variance, which is 1/400 of coin weight. If the average weight of coins is lower than the standard, resulting in surplus gold for the mint, the trial will punish the person in charge of the mint. But if the variance is higher than the specified value, then there will be overweight coins, which are used for private melting and recovering gold, bringing excess profits to the mint. This unreasonable variance regulation lasted for nearly 600 years, so this trial is considered one of the most dangerous candidates for De Moivre\'s equation.

The second problem is also a mistake that we Chinese people often make, which is to think that living in rural areas has a lower probability of getting sick than cities. Howard Wainer used statistical formula De Moivre to prove why both counties with lowest and highest kidney cancer rates in America are rural areas. De Moivre\'s equation shows that The variation of the mean is inversely proportional to the sample size, so small counties display much greater variation than large counties. A county with, say, 100 inhabitants that has no cancer deaths would be in the lowest category. But if it has 1 cancer death it would be among the highest. Counties like Los Angeles, Cook or Miami-Dade with millions of inhabitants do not bounce around like that.

The third example is The Small-Schools Movement. I remember when I was studying, many people thought that small schools would have better teaching quality, but Howard Wainer said this was inaccurate. The third example introduces that in the late 20th century, there was dissatisfaction with large schools in America and began to support small schools to provide better education. Among them, small schools help improve students\' performance, which is one kind of evidence to support small schools. Howard Wainer studied performance and size of all public schools in Pennsylvania and found some results related to relationship between school size and student performance. The author points out that small schools are overrepresented among both well-performing and poorly performing schools. However, the author also points out that this problem is more complicated than it appears because there is not always a simple linear relationship between size and student performance. Small schools have similar overrepresentation at both extremes but this time regression line shows significant positive slope; overall students at large schools perform better. This is also not surprising because very small high schools cannot offer as wide a range of courses or as many highly specialized teachers as large schools. Finally, the author points out that education should be driven by facts rather than theory and study the impact of school size on student performance in depth. If we do not understand statistics and variance rules, we are likely to draw wrong conclusions, which is very dangerous for education.

The fourth example is gender difference, which is an old topic. In every country, there seems to be a situation where there are more men than women in the upper class and also in the lower class. Although many people are not aware of the lower class, and think it is unfair and then there is a gender opposition. But this example mainly discusses the different performance and variability of men and women in academic test scores. Studies have shown that there are more men than women in the high-end distribution of scores, and that men\'s scores have greater variance, which does not mean that men are more intelligent, but that there is a huge variability difference between genders. At the same time, through genetic analysis, it is shown that male animals contribute more genetic variability due to competition and selection in species reproduction. The example in the article is very vivid: Think of the alpha-male lion surrounded by a pride of females, with lesser males wandering aimlessly and alone in the forest roaring in frustration. One way to increase the likelihood of offspring being selected to reproduce is to have large variance among them. Thus evolutionary pressure would reward larger variation for males relative to females.

As a paper discussing the potential dangers of some mathematical statistical equations, this article tells us that understanding the limitations and potential misuse of mathematical equations is important for mathematics and related fields, because it can help prevent errors and promote accurate analysis and decision making. Howard Wainer used some historical examples and explanations of mathematical equations to support his argument, and his analysis method was vivid, close to life, and mathematically impeccable. He very perfectly demonstrated the problem that misunderstanding of equations related to the law of large numbers may bring unpredictable consequences.

at the same time, The article is well-organized and easy to understand, with clear titles and subtitles that help to guide the reader through the content. The author provides historical examples and explanations of mathematical equations to support their argument, which helps to make the content more accessible to readers who may not have a strong mathematical background. The author also uses visual aids such as graphs and tables to illustrate the data and concepts discussed in the article.

I lists some strengths and some weaknesses of the article:

Strengths:

1. The article discusses a thought-provoking topic that is relevant to a wide range of fields such as mathematics, statistics and social sciences.

2. The author provides historical examples and explanations of mathematical equations to support their argument, which helps to make the content more accessible to readers who may not have a strong mathematical background.

3. The author raises important questions about the limitations and potential misuse of mathematical equations, which can help to promote more accurate analysis and decision making in various domains.

4. The article is well-organized and easy to understand, with clear titles and subtitles that help to guide the reader through the content.

Weaknesses:

1. The author does not provide a comprehensive overview of the potential dangers of mathematical equations, but focuses on a few specific examples. This may limit the scope and applicability of the content for readers who are interested in a broader discussion of the topic.

2. The article does not provide any practical advice or solutions to address the potential dangers of mathematical equations, which may leave readers uncertain about how to apply the information provided in the document.

3.The article does not provide a comprehensive overview of the potential dangers of mathematical equations, but focuses on a few specific examples. This may limit the scope and applicability of the content for readers who are interested in a broader discussion of the topic.

4.The article does not provide any practical advice or solutions to address the potential dangers of mathematical equations, which may leave readers uncertain about how to apply the information provided in the document.

5.Only lists the harms to attract our attention, but does not analyze the benefits of statistical equations for human society. The advantage is that it explains several phenomena that occur in daily life, and analyzes the essence of the problem through statistical equations. Although it is not possible to be 100% sure that this problem is caused by it, it can provide some evidence. It makes us aware of the dangers of improper use of statistical equations.

 

In generally, the author have presented a balanced and objective discussion of the potential dangers of certain mathematical equations. The author provides historical examples and explanations of mathematical equations to support their argument, and acknowledges the potential benefits and limitations of these equations. The author also raises important questions about the assumptions and uncertainties that underlie mathematical models, and encourages readers to approach these models with caution and critical thinking. Overall, the author\'s discussion of the topic is objective and well-supported by evidence.

Through this article, I hope that we can clearly understand why some phenomena in daily life seem reasonable but are actually not, and I can analyze these problems using statistical methods like Howard Wainer. Furthermore, we can gain a deeper understanding of the significance of variance and learn about the harm it can cause. However, using variance can also bring some benefits, which requires us to further analyze and discuss together!

Statistical analysis is vital in understanding the world around us. We often encounter situations where things seem to make sense, but after careful examination, we realize that our initial perceptions were incorrect. This is where statistics comes in. By analyzing data using statistical methods, we can identify patterns, trends and correlations that would otherwise go unnoticed. This not only helps us gain a deeper understanding of the world around us, but it also aids us in making informed decisions.

Variance is an important concept in statistics. It represents the amount of variability or spread in a set of data. However, variance can be misleading when used incorrectly. For example, relying solely on variance to interpret data can lead to oversimplified conclusions and incorrect decisions. It is essential to understand the limitations of variance when analyzing data and to use it in conjunction with other statistical methods to get a more accurate picture of the data.

In conclusion, statistics is a powerful tool that can help us understand the world around us. However, it is crucial to use statistics appropriately, and to consider all factors in data analysis to make informed decisions. By doing so, we can avoid errors in our judgment, minimize risks, and make better decisions that benefit us all.

Python turtle绘图实例分析

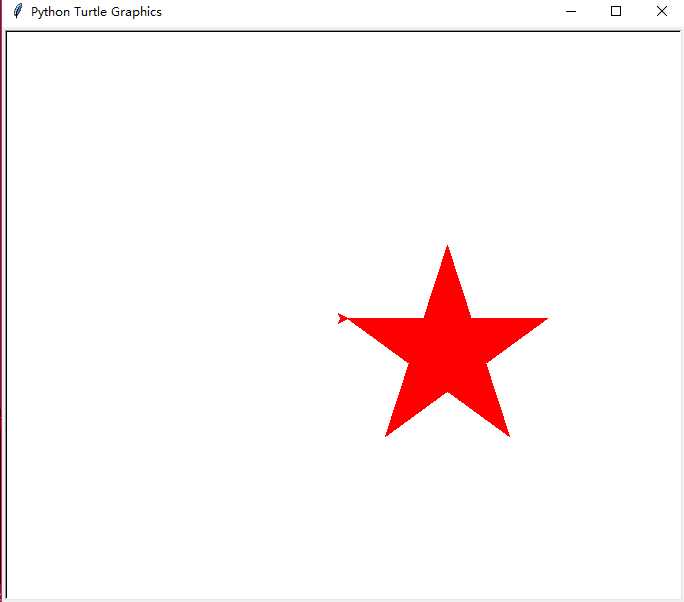
画一个红色的五角星

from turtle import *
color(‘red‘,‘red‘)
begin_fill()
for i in range(5):
    fd(200)
    rt(144)

end_fill()
done()

效果图：

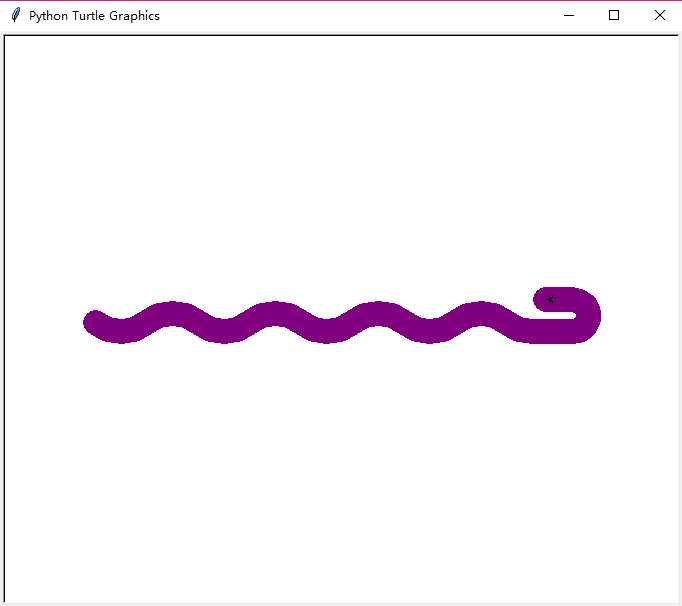
画一条蟒蛇

#PythonDraw.py
import turtle
#turtle.setup(650,350,200,200)
turtle.penup()
turtle.fd(-250)
turtle.pendown()
turtle.pensize(25)
turtle.pencolor("purple")
turtle.seth(-40)
for i in range(4):
    turtle.circle(40,80)
    turtle.circle(-40,80)
turtle.circle(40,80/2)
turtle.fd(40)
turtle.circle(16,180)
turtle.fd(40*2/3)

效果图：

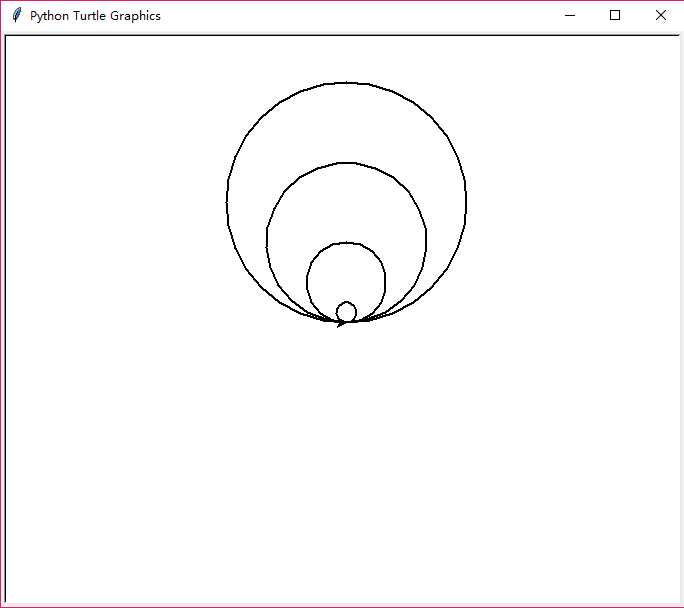
画一组内切圆

import turtle
turtle.pensize(2)
turtle.circle(10)
turtle.circle(40)
turtle.circle(80)
turtle.circle(120)

效果图：

画一个社会人小猪佩奇，代码是借鉴某位大佬的

from turtle import *
def nose(x,y):
    pu()
    goto(x,y)
    pd()
    seth(-30)
    begin_fill()
    a=0.4
    for i in range(120):
        if 0<=i<30 or 60<=i<90:
            a=a+0.08
            lt(3)
            fd(a)
        else:
            a=a-0.08
            lt(3)
            fd(a)
    end_fill()

    pu()
    seth(90)
    fd(25)
    seth(0)
    fd(10)
    pd()
    pencolor(255,155,192)
    seth(10)
    begin_fill()
    circle(5)
    color(160,82,45)
    end_fill()

    pu()
    seth(0)
    fd(20)
    pd()
    pencolor(255,155,192)
    seth(10)
    begin_fill()
    circle(5)
    color(160,82,45)
    end_fill()

def head(x,y):
    color((255,155,192),"pink")
    pu()
    goto(x,y)
    seth(0)
    pd()
    begin_fill()
    seth(180)
    circle(300,-30)
    circle(100,-60)
    circle(80,-100)
    circle(150,-20)
    circle(60,-95)
    seth(161)
    circle(-300,15)
    pu()
    goto(-100,100)
    pd()
    seth(-30)
    a=0.4
    for i in range(60):
        if 0<=i<30 or 60<=i<90:
            a=a+0.08
            lt(3)
            fd(a)
        else:
            a=a-0.08
            lt(3)
            fd(a)
    end_fill()

def ears(x,y):
    color((255,155,192),"pink")
    pu()
    goto(x,y)
    pd()
    begin_fill()
    seth(100)
    circle(-50,50)
    circle(-10,120)
    circle(-50,54)
    end_fill()

    pu()
    seth(90)
    fd(-12)
    seth(0)
    fd(30)
    pd()
    begin_fill()
    seth(100)
    circle(-50,50)
    circle(-10,120)
    circle(-50,56)
    end_fill()

def eyes(x,y):
    color((255,155,192),"white")
    pu()
    seth(90)
    fd(-20)
    seth(0)
    fd(-95)
    pd()
    begin_fill()
    circle(15)
    end_fill()

    color("black")
    pu()
    seth(90)
    fd(12)
    seth(0)
    fd(-3)
    pd()
    begin_fill()
    circle(3)
    end_fill()

    color((255,155,192),"white")
    pu()
    seth(90)
    fd(-25)
    seth(0)
    fd(40)
    pd()
    begin_fill()
    circle(15)
    end_fill()

    color("black")
    pu()
    seth(90)
    fd(12)
    seth(0)
    fd(-3)
    pd()
    begin_fill()
    circle(3)
    end_fill()

def cheek(x,y):
    color((255,155,192))
    pu()
    goto(x,y)
    pd()
    seth(0)
    begin_fill()
    circle(30)
    end_fill()

def mouth(x,y):
    color(239,69,19)
    pu()
    goto(x,y)
    pd()
    seth(-80)
    circle(30,40)
    circle(40,80)

def body(x,y):
    color("red",(255,99,71))
    pu()
    goto(x,y)
    pd()
    begin_fill()
    seth(-130)
    circle(100,10)
    circle(300,30)
    seth(0)
    fd(230)
    seth(90)
    circle(300,30)
    circle(100,3)
    color((255,155,192),(255,100,100))
    seth(-135)
    circle(-80,63)
    circle(-150,24)
    end_fill()

def hands(x,y):
    color((255,155,192))
    pu()
    goto(x,y)
    pd()
    seth(-160)
    circle(300,15)
    pu()
    seth(90)
    fd(15)
    seth(0)
    fd(0)
    pd()
    seth(-10)
    circle(-20,90)

    pu()
    seth(90)
    fd(30)
    seth(0)
    fd(237)
    pd()
    seth(-20)
    circle(-300,15)
    pu()
    seth(90)
    fd(20)
    seth(0)
    fd(0)
    pd()
    seth(-170)
    circle(20,90)

def foot(x,y):
    pensize(10)
    color((240,128,128))
    pu()
    goto(x,y)
    pd()
    seth(-90)
    fd(40)
    seth(-180)
    color("black")
    pensize(15)
    fd(20)

    pensize(10)
    color((240,128,128))
    pu()
    seth(90)
    fd(40)
    seth(0)
    fd(90)
    pd()
    seth(-90)
    fd(40)
    seth(-180)
    color("black")
    pensize(15)
    fd(20)

def tail(x,y):
    pensize(4)
    color((255,155,192))
    pu()
    goto(x,y)
    pd()
    seth(0)
    circle(70,20)
    circle(10,330)
    circle(70,30)
    
    
def setting():
    pensize(4)
    hideturtle()
    colormode(255)
    color((255,155,192),"pink")
    setup(840,500)
    speed(10)

def main():
    setting()
    nose(-100,100)
    head(-69,167)
    ears(0,160)
    eyes(0,140)
    cheek(80,10)
    mouth(-20,30)
    body(-32,-8)
    hands(-56,-45)
    foot(2,-177)
    tail(148,-155)
    done()

main()
            

效果极佳：

简单总结一下好了，其实turtle库还是非常有用的，以后可以画张很有创意的图片去表白女神了，讲不好那天就用上了呢：

显示器和turtle窗体的左上角都是原点
turtle.setup(width,height,startx,starty)设置窗体大小及位置，后面两个参数可选，非必需
空间坐标：绝对坐标：右方向x轴，上方向为y轴，正中心为原点，turtle.goto(x,y)让在任何位置的海龟到达指定的位置
海龟坐标：turtle.fd(d)海龟向前行多少像素
turtle.bk(d)向海龟的反方向运行
turtle.circle(r,angle)以海龟左边的某一点为圆心进行曲线运行
角度坐标：绝对角度：turtle.seth(angle)angle为绝对度数，表示改变海龟的运行方向
海龟角度：turtle.right(angle),turtle.left(angle)改变海龟的运行方向
RGB体系：turtle.colormode(mode)mode=1.0则改用0和1表示，mode=255则改用255和0表示，默认为小数
库引用：import <库名>,from <库名> import *或者from <库名> import <函数名>,import <库名> as <库别名>
画笔控制函数：turtle.penup()别名：turtle.pu()抬起画笔，turtle.pendown()别名：turtle.pd()落下画笔，turtle.pensize(width)别名：turtle.width(width)设置画笔宽度，turtle.pencolor(color)设置画笔颜色，color有三种方式，颜色字符串，或者RGB小数值，或者RGB元组值，例如：turtle.pencolor((0.63,0.13,0.94))
运动控制函数:turtle.circle(r,angle),r（海龟左方向）表示半径，angle表示绘制的角度，默认是360度
方向控制函数：turtle.seth(angle)改变海龟的行进方向，顺时针转向