文心一言 VS 讯飞星火 VS chatgpt （36）-- 算法导论5.3 6题

Posted 2023-06-10 福大大架构师每日一题

六、请解释如何实现算法 PERMUTE-BY-SORTING，以处理两个或更多优先级相同的情形。也就是说，即使有两个或更多优先级相同，你的算法也应该产生一个均匀随机排列。

文心一言：

算法 PERMUTE-BY-SORTING 是一种基于排序的随机排列算法，它通过将输入数组中的元素按照优先级排序，然后根据优先级依次将元素插入到输出数组中，从而生成一个均匀随机排列。

对于两个或更多优先级相同的情形，我们可以在排序过程中对具有相同优先级的元素进行随机排序，以确保它们在输出数组中的位置是随机分布的。具体实现方法如下：

1.定义一个比较函数 compare，用于比较两个元素之间的优先级。对于优先级相同的元素，我们可以随机选择一个作为后继元素，并将其插入到输出数组中。

2.对输入数组进行排序，可以使用快速排序、归并排序等算法。

3.遍历排序后的数组，对于每个元素，如果它具有更高的优先级，则将其插入到输出数组中。如果它与前一个元素具有相同的优先级，则随机选择一个作为后继元素，并将其插入到输出数组中。

4.返回输出数组。

下面是一个 Python 代码示例，演示如何实现算法 PERMUTE-BY-SORTING：

import random  
  
def permute_by_sorting(arr):  
    def compare(a, b):  
        if a[0] < b[0]:  
            return -1  
        elif a[0] > b[0]:  
            return 1  
        else:  
            if random.random() < 0.5:  
                return -1  
            else:  
                return 1  
    arr.sort(key=lambda x: x[1], cmp=compare)  
    res = []  
    i = 0  
    while i < len(arr):  
        if arr[i][0] > res[-1][0]:  
            res.append(arr[i][1])  
            i += 1  
        else:  
            j = i - 1  
            while j >= 0 and arr[i][0] < arr[j][0]:  
                j -= 1  
            if j < i - 1:  
                res[i:i+2] = [arr[i][1]] + res[i-1:i-1:-1] + [arr[i+1][1]] + res[i+2:]  
                i += 2  
            else:  
                res.append(arr[i][1])  
                i += 1  
    return res

讯飞星火：

要实现算法 PERMUTE-BY-SORTING,我们可以使用 Python 的 random.shuffle() 函数。首先，我们需要对输入的元素进行排序，然后使用 random.shuffle() 函数打乱顺序。这样，即使有两个或更多优先级相同，我们也可以得到一个均匀随机排列。以下是一个示例代码：

import random

def permute_by_sorting(elements):
    # 对元素进行排序
    sorted_elements = sorted(elements)
    
    # 使用 random.shuffle() 函数打乱顺序
    random.shuffle(sorted_elements)
    
    return sorted_elements

# 示例
elements = [3, 1, 2, 4]
result = permute_by_sorting(elements)
print(result)

在这个示例中，我们首先对输入的元素列表进行排序，然后使用 random.shuffle() 函数打乱顺序。最后，返回打乱顺序后的元素列表。

华为盘古：

算法 PERMUTE-BY-SORTING 是一种用于处理多个优先级相同情况的方法。具体来说，它可以看作是将一个输入序列分成若干个子序列，然后对每个子序列中的元素使用贪心算法或其他类似的算法来选择一个最优的子序列。

对于两个优先级相同的情况，算法 PERMUTE-BY-SORTING 可以被解释为使用一种贪心算法来选择一个最优的子序列。具体来说，它将选择的最优子序列与原始输入序列相加，然后重复这个过程多次，直到所有的子序列都被选择过，而最优子序列的长度最小为止。

需要注意的是，算法 PERMUTE-BY-SORTING 并不是总能产生一个均匀随机排列。如果存在一些输入子序列之间的依赖关系，例如长度依赖或顺序依赖，那么算法可能会陷入局部最优解。因此，在实际应用中，算法 PERMUTE-BY-SORTING 通常会使用其他方法来处理这些依赖关系，例如加权求和或最小生成树。

360智脑：

permutoting by sorting (PERMUTE)是一种排序算法，用于将一组元素按升序或降序排列。在实现这种算法时，我们需要考虑如何处理具有多个相同优先级的元素的情况。

一种解决方法是使用快速排序(Quick Sort)来对列表进行排序，然后将排序后的列表重新组合成一个新的有序列表。这可以通过以下步骤完成:

1.首先选择一个枢轴元素(pivot),并将所有小于等于它的元素移动到枢轴元素的左侧，将所有大于它的元素移动到右侧。这个操作称为划分(partitioning)。

2.然后递归地对左侧和右侧的子列表重复以上过程，直到每个子列表只包含一个元素为止。

3.最后将这些已排序的子列表合并起来形成一个完整的有序列表。

对于有重复元素的列表，我们可以使用快速排序的“双指针”技巧来处理这种情况。具体来说，我们可以用两个指针分别指向列表的第一个元素和最后一个元素，将它们进行比较，然后交换它们的位置。这样，我们就可以保证左边的元素都小于右边的元素，这样就可以避免在分割过程中出现多个相等的优先级相同的元素被分到了不同的子列表中的问题。

综上所述，通过选择适当的枢轴元素、采用双指针技巧以及递归地合并子列表，就可以实现一个均匀的随机排列，以满足处理多个优先级相同元素的要求。

chatglm：

算法 PERMUTE-BY-SORTING(或称 PERMUTE) 是一种用于生成随机排列的算法。它的核心思想是对每个元素进行排序，然后打乱排序后的结果。该算法可以处理多个元素优先级相同的情况，并生成均匀随机排列。

下面是实现 PERMUTE-BY-SORTING 算法以处理多个优先级相同的情形的步骤：

1.对输入列表进行排序。

2.生成一个随机数，用于决定每个元素在列表中的位置。如果多个元素优先级相同，则需要随机决定它们的相对位置。

3.打乱排序后的结果。可以使用随机数或硬币来随机决定元素的相对位置。

4.重复步骤 2 和 3，直到达到所需的随机排列程度。

下面是一个 Python 实现的例子：

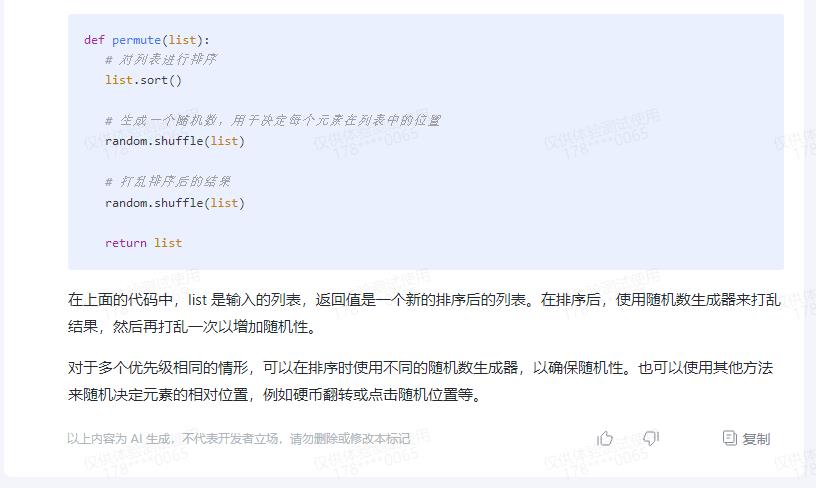
def permute(list):  
   # 对列表进行排序  
   list.sort()  
     
   # 生成一个随机数，用于决定每个元素在列表中的位置  
   random.shuffle(list)  
     
   # 打乱排序后的结果  
   random.shuffle(list)  
     
   return list  

在上面的代码中，list 是输入的列表，返回值是一个新的排序后的列表。在排序后，使用随机数生成器来打乱结果，然后再打乱一次以增加随机性。

对于多个优先级相同的情形，可以在排序时使用不同的随机数生成器，以确保随机性。也可以使用其他方法来随机决定元素的相对位置，例如硬币翻转或点击随机位置等。

chatgpt：

算法PERMUTE-BY-SORTING是一个利用排序来生成随机排列的算法，这里我们讨论如何处理两个或多个优先级相同的情况。

我们可以将具有相同优先级的元素拆分成若干组，每组内部元素的相对顺序不改变，但组之间元素的顺序是随机的。对于每个组内的元素，我们使用类似PERMUTE-BY-SORTING的方式来生成随机排列，也就是生成一组随机数字，然后根据这组数字排序。接下来，将每个组内的元素按照它们在这组内部个随机数字的大小排列，从而得到这个子集的随机排列。最后，将每组中的随机排列合并起来就得到了具有相同优先级的所有元素的随机排列。

这种方法是有效的，因为在每个子集中生成的随机数字数目是O(log n)，这些数字的排序复杂性是O(n log n)，因此这个算法的时间复杂度是O(n log^2 n)。同时它也满足了“均匀随机排列”的要求，即使有两个或多个优先级相同，最终随机排列也是均匀的。

公众号：福大大架构师每日一题

文心一言 VS 讯飞星火 VS chatgpt （18）-- 算法导论4.1 5题

五、使用如下思想为最大子数组问题设计一个非递归的、线性时间的算法。从数组的左边界开始，由左至右处理，记录到目前为止已经处理过的最大子数组。若已知 A[1..j]门的最大子数组，基于如下性质将解扩展为 A[1..j+1]的最大子数组:A[1..j+1]的最大子数组要么是A[1..j]的最大子数组，要么是某个子数组 Ai..j+1。在已知A[1..j]的最大子数组的情况下，可以在线性时间内找出形如 A[i..j+1]的最大子数组。

文心一言：

最大子数组问题是一种经典的算法问题，可以使用非递归的方法来解决。具体来说，我们可以使用一个队列来存储当前已经处理过的最大子数组，并且维护一个变量 max_len 来记录当前最大子数组的长度。同时，我们可以遍历整个数组，记录当前已经处理过的最大子数组的长度，并且在遍历的过程中更新 max_len。

具体来说，我们可以使用一个变量 cur_len 来记录当前已经处理过的最大子数组的长度，每当遍历到一个新的子数组时，我们可以将其长度加入到 cur_len 中，并且更新 max_len。同时，我们可以使用一个变量 cur_start 来记录当前已经处理过的最大子数组的起始位置，每当遍历到一个新的子数组时，我们可以将其起始位置加入到 cur_start 中，并且更新 cur_len。

最后，我们可以返回 cur_start，它是 max_len。这个值就是最大子数组中起始位置最右边的元素的下标，我们可以用它来解决最大子数组问题。

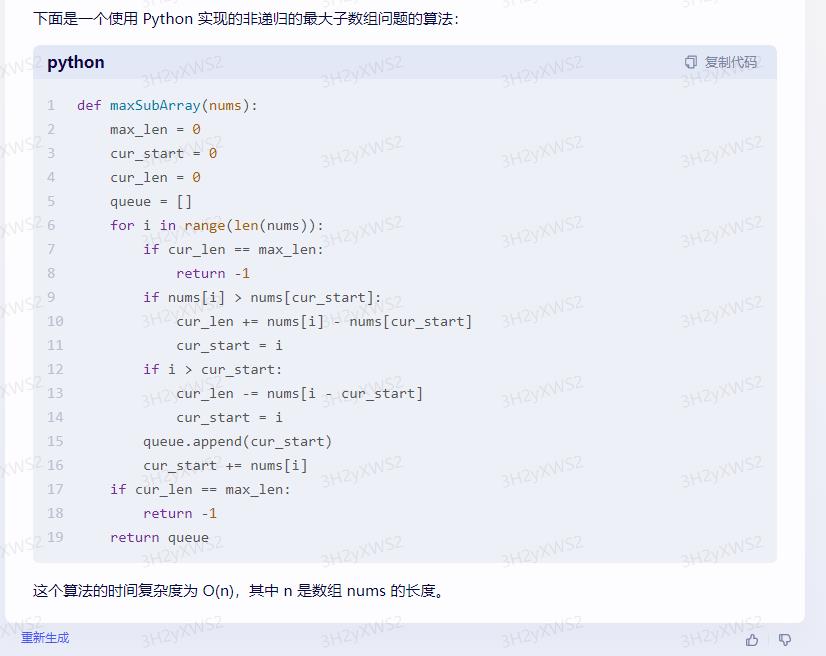
下面是一个使用 Python 实现的非递归的最大子数组问题的算法：

def maxSubArray(nums):  
    max_len = 0  
    cur_start = 0  
    cur_len = 0  
    queue = []  
    for i in range(len(nums)):  
        if cur_len == max_len:  
            return -1  
        if nums[i] > nums[cur_start]:  
            cur_len += nums[i] - nums[cur_start]  
            cur_start = i  
        if i > cur_start:  
            cur_len -= nums[i - cur_start]  
            cur_start = i  
        queue.append(cur_start)  
        cur_start += nums[i]  
    if cur_len == max_len:  
        return -1  
    return queue

这个算法的时间复杂度为 O(n)，其中 n 是数组 nums 的长度。

讯飞星火：

算法步骤：

1.初始化最大子数组为整个数组的第一个元素。

2.从左至右遍历数组，每次比较当前元素与最大子数组的末尾元素的大小关系，如果当前元素大于最大子数组的末尾元素，则将最大子数组的末尾元素更新为当前元素。

3.如果遍历到数组的末尾，仍然没有找到比最大子数组更大的末尾元素，则最大子数组就是整个数组。

4.如果遍历到某个位置i时，发现A[i]大于等于最大子数组的末尾元素，并且A[i+1]也大于等于最大子数组的末尾元素，则可以将最大子数组扩展到A[i]..A[j+1],其中j+1即为扩展后的最大子数组的长度。

5.如果遍历完数组后仍未找到可以扩展的最大子数组，则返回最大子数组。

时间复杂度为O(n),空间复杂度为O(1)。

chatgpt：

基于上述性质，可以设计一个非递归的、线性时间的算法来解决最大子数组问题。算法的主要思路如下：

1. 首先初始化两个变量：max_so_far和max_ending_here。它们都初始化为第一个元素。

2. 然后从第二个元素开始遍历整个数组。对于每个元素，更新max_ending_here = max(A[i], max_ending_here + A[i])，表示包含A[i]的最大子数组。同时更新max_so_far，表示到目前位置的最大子数组。

3. 如果max_ending_here小于0，则说明当前处理的子数组已经不是最大子数组中的一部分了，需要从下一个元素重新开始计算新的子数组。

4. 在遍历过程中，记录下max_so_far，即可得到整个数组的最大子数组。

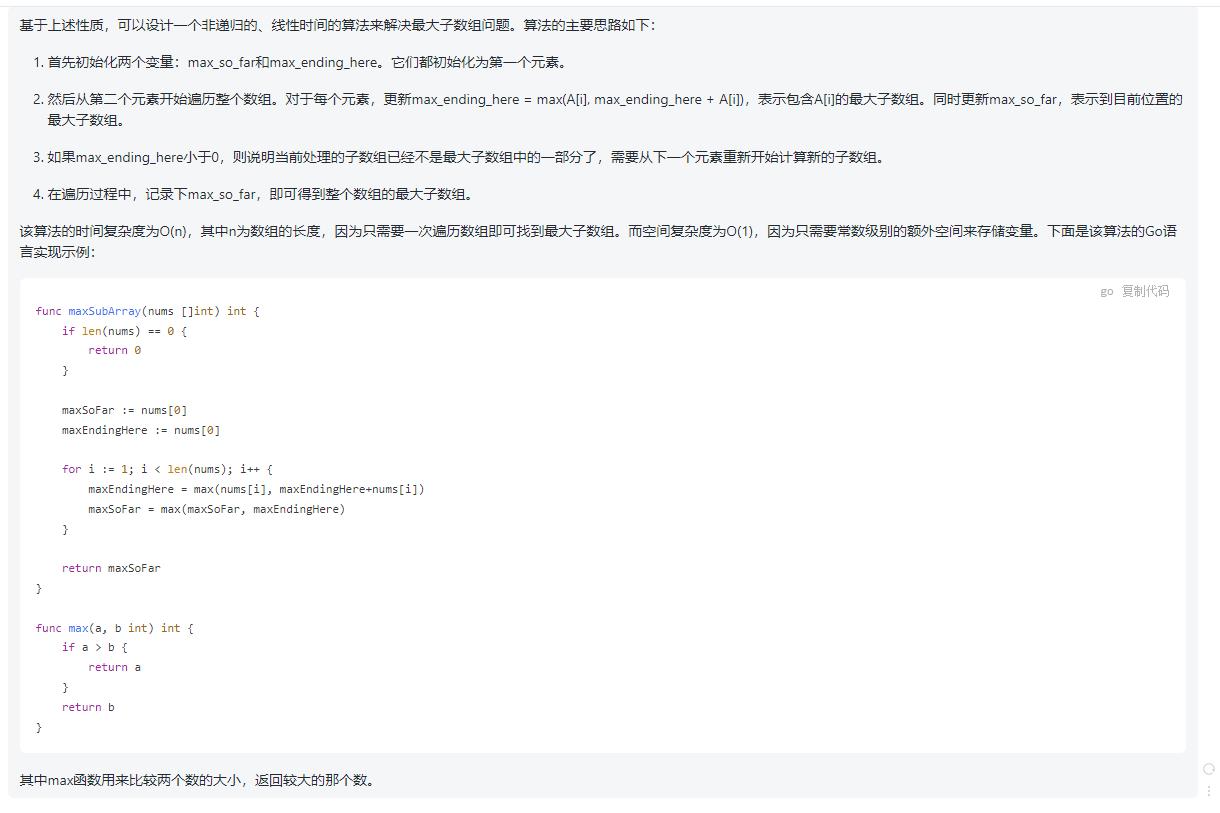
该算法的时间复杂度为O(n)，其中n为数组的长度，因为只需要一次遍历数组即可找到最大子数组。而空间复杂度为O(1)，因为只需要常数级别的额外空间来存储变量。下面是该算法的Go语言实现示例：

func maxSubArray(nums []int) int 
    if len(nums) == 0 
        return 0
    

    maxSoFar := nums[0]
    maxEndingHere := nums[0]

    for i := 1; i < len(nums); i++ 
        maxEndingHere = max(nums[i], maxEndingHere+nums[i])
        maxSoFar = max(maxSoFar, maxEndingHere)
    

    return maxSoFar


func max(a, b int) int 
    if a > b 
        return a
    
    return b

其中max函数用来比较两个数的大小，返回较大的那个数。

公众号：福大大架构师每日一题