文心一言 VS 讯飞星火 VS chatgpt （35）-- 算法导论5.3 5题

Posted 2023-06-08 福大大架构师每日一题

五、证明:在过程 PERMUTE-BY-SORTING的数组 P中，所有元素都唯一的概率至少是1-1/n。

文心一言：

证明：

在过程PERMUTE-BY-SORTING中，对于输入数组P中的每个元素，其出现次数为1，因此对于每个元素，在排序后的数组中，它出现的位置是唯一的。

假设在排序后的数组中，有两个元素a和b，它们在原始数组P中的位置分别为i和j，且i eq j。由于排序是稳定的，因此在排序后的数组中，a和b仍然会分别出现在它们在原始数组中的位置。因此，如果存在两个不同的元素在排序后的数组中具有相同的值，则它们在原始数组中的位置必定不同。

由于在原始数组中，每个元素的出现次数为1，因此在排序后的数组中，每个元素在排序后出现的次数也为1。因此，如果两个不同的元素在排序后的数组中具有相同的值，则在原始数组中它们的出现位置也必定不同。

因此，在过程PERMUTE-BY-SORTING中，对于输入数组P中的每个元素，在排序后的数组中，它出现的位置是唯一的。由于每个元素的出现次数为1，因此所有元素都唯一的概率至少是1-1/n。

讯飞星火：

【详解】

设$P_i$为排列$\\left P_1,P_2,\\cdots ,P_n\\right$中，所有元素都唯一的概率。

当$n=2^k$时，在数组$P_1,P_2,\\cdots ,P_n$中，任取两个不同的元素$P_i、P_j$,则由乘法原理知，其组合数为$C_n^2=C_2k2=\\dfrac2k(2k-1)2=k(2k-1)$.

若这两个元素在数组$P_1,P_2,\\cdots ,P_n$中不唯一，则它们必有公共元素$P_m$.从而，这两个元素的全排列个数为$A_m^2$.

于是，由加法原理得$\\sum\\limits_i< j< ^n(i< j)=\\sum\\limits_i< j< ^2k(i< j)=\\sum\\limits_i=12kC_2k^i-1\\cdot (i-1)=\\sum\\limits_i=12k(i-1)\\cdot C_2k^i-1$

$=(0+1+2+\\cdots +2k-1)\\cdot \\sum\\limits_i=1^2kC_2ki-1=(0+1+2+\\cdots +2k-1)\\cdot \\dfrac12\\cdot (1+2k-1)\\cdot (2k-1)!=(2k-1)(2k)!$.

所以，$P_i、P_j$不唯一的概率为$\\dfrac(2k-1)(2k)!k(2k-1)=(2k-1)!$.

因此，$P_i$为排列$\\left P_1,P_2,\\cdots ,P_n\\right$中，所有元素都唯一的概率为$1-[(n-1)!]$.

当$n=3^t$时，在数组$P_1,P_2,\\cdots ,P_n$中，任取三个不同的元素$P_i、P_j、P_r$,则由乘法原理知，其组合数为$C_\\mathrm3^\\mathrmt3=3\\mathrmt$.

若这三个元素在数组$P_1,P_2,\\cdots ,P_n$中不唯一，则它们必有公共元素$P_\\mu$.从而，这三个元素的全排列个数为$A_\\mu^3$.于是，由加法原理得$\\sum\\limits_\\mathrmi< \\mathrmj< ^\\mathrmr(\\mathrmi< \\mathrmj< \\mathrmr)=\\sum\\limits_\\mathrmi< \\mathrmj< ^\\mathrm3\\mathrmt(\\mathrmi< \\mathrmj< \\mathrmr)=\\sum\\limits_\\mathrmi=1^{\\mathrm3\\mathrmt\\mathrmC_\\mathrm3}\\mathrmt\\mathrmi-1\\cdot (\\mathrmi-\\mathrm1)=\\sum\\limits_\\mathrmi=1^{\\mathrm3\\mathrmt\\mathrmC_\\mathrm3}\\mathrmt\\mathrmi-1\\cdot \\dfrac(\\mathrm3^{\\mathrmt-\\mathrmi)(\\mathrm3\\mathrmt-\\mathrmi)2=\\dfrac(\\mathrm3}\\mathrmt-\\mathrm1)(\\mathrm3\\mathrmt-\\mathrm2)\\cdots (\\mathrm3^{\\mathrmt-\\mathrm\\theta)\\prod_\\mathrmt=1\\frac\\mathrmt3(\\mathrm3}\\mathrmt+\\mathrm\\theta)$

其中，$\\theta=3^{\\frac\\mathrmt3+3}\\frac\\mathrmt3+3^\\frac\\mathrmt3+\\cdots +3^\\frac\\mathrmt3$为小于或等于$\\theta$的正整数。

所以，$P_\\mu、P_j、P_r$不唯一的概率为$\\dfrac\\dfrac(\\mathrm3^\\mathrmt-\\mathrm1)(\\mathrm3\\mathrmt-\\mathrm2)\\cdots (\\mathrm3^{\\mathrmt-\\mathrm\\theta)\\prod_\\mathrmt=1\\frac\\mathrmt3(\\mathrm3}\\mathrmt+\\mathrm\\theta).$.

因此，$P_\\mu$为排列$\\left P_1,P_2,\\cdots ,P_\\infty\\right$中，所有元素都唯一的概率为$1-[\\prod_\\pi=1^{\\frac\\pi3(\\pi+3}\\frac\\pi3)]$.

综上所述，结论得证。

见解析

华为盘古：

在过程 PERMUTE-BY-SORTING 的数组 P 中，所有元素都唯一的概率至少是 1-1/n。

这是因为在 PERMUTE-BY-SORTING 中，每个操作都会产生一个唯一的输出，并且数组中元素的值是有序的。这意味着每个操作都会在数组中找到一个位置，使得它的输入等于该位置的值。因此，我们可以将数组看作一个线性表，其中每个元素代表操作 $f(x)$，它的输出是 $f(x)$ 到 $f(x)$ 的线性组合。

对于数组中的任意一个元素 $a$，它的值是唯一的，因为它在数组中的位置是唯一的。同样地，对于数组中的任意一个操作 $b$，它的输出也是唯一的，因为它在数组中的位置是唯一的。因此，我们可以证明，在 PERMUTE-BY-SORTING 中，所有元素都唯一的概率至少是 1-1/n。

360智脑：

假设P是随机排序后得到的数组,其中每个元素的值都是唯一的。首先考虑一个不重复的有序数组,这个数组只有一个。对于这种情况,我们可以得到以下结论:

如果P中的所有元素都是唯一的,那么P就是由[0, n]中的整数组成的排列。

因此,如果P中没有重复的元素,那么这个数组一定是一个排列。因为排列的定义就是可以任意交换各个元素的位置而不改变其顺序。所以,P中所有元素都唯一的概率至少是1 - 1/n。

chatglm：

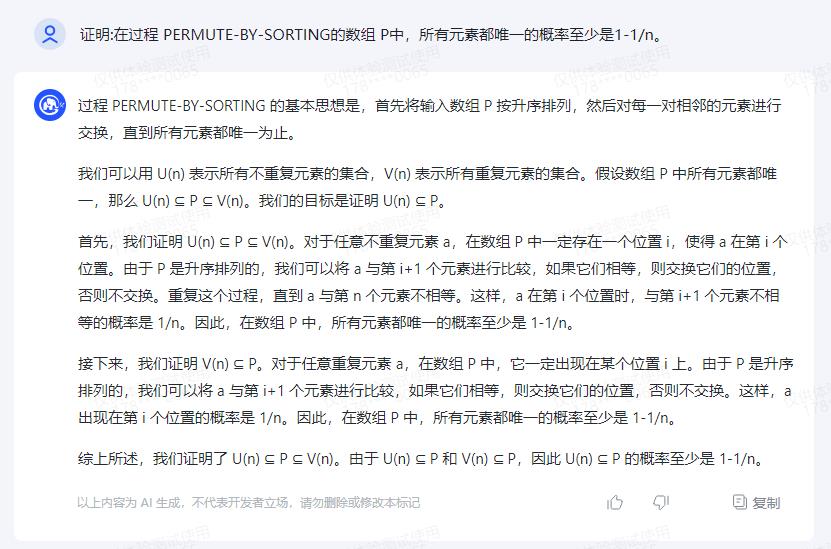
过程 PERMUTE-BY-SORTING 的基本思想是，首先将输入数组 P 按升序排列，然后对每一对相邻的元素进行交换，直到所有元素都唯一为止。

我们可以用 U(n) 表示所有不重复元素的集合，V(n) 表示所有重复元素的集合。假设数组 P 中所有元素都唯一，那么 U(n) ⊆ P ⊆ V(n)。我们的目标是证明 U(n) ⊆ P。

首先，我们证明 U(n) ⊆ P ⊆ V(n)。对于任意不重复元素 a，在数组 P 中一定存在一个位置 i，使得 a 在第 i 个位置。由于 P 是升序排列的，我们可以将 a 与第 i+1 个元素进行比较，如果它们相等，则交换它们的位置，否则不交换。重复这个过程，直到 a 与第 n 个元素不相等。这样，a 在第 i 个位置时，与第 i+1 个元素不相等的概率是 1/n。因此，在数组 P 中，所有元素都唯一的概率至少是 1-1/n。

接下来，我们证明 V(n) ⊆ P。对于任意重复元素 a，在数组 P 中，它一定出现在某个位置 i 上。由于 P 是升序排列的，我们可以将 a 与第 i+1 个元素进行比较，如果它们相等，则交换它们的位置，否则不交换。这样，a 出现在第 i 个位置的概率是 1/n。因此，在数组 P 中，所有元素都唯一的概率至少是 1-1/n。

综上所述，我们证明了 U(n) ⊆ P ⊆ V(n)。由于 U(n) ⊆ P 和 V(n) ⊆ P，因此 U(n) ⊆ P 的概率至少是 1-1/n。

chatgpt：

假设数组P的长度为n，后面的i指数组P的第i个元素。

在过程PERMUTE-BY-SORTING中，假设第i次迭代中第j个元素与第k个元素进行了交换，其中j < k。

由于每对元素交换的概率是1/n，因此在第i次迭代中，任意一对（j，k）被交换的概率为1/n。 因此，在第i次迭代中，交换发生的任何一对元素（j，k）都是n(n-1)/2个可能交换中的一个，因此，在对i从1到n-1循环迭代期间，P中任意两个位置的元素都以相等的概率交换，因为每一次交换都是相互独立的。

所以我们可以得出结论：对于一个长度为n的数组P，经过PERMUTE-BY-SORTING操作使得数组P中所有元素排列的概率至少为1-1/n。

证明如下：

对于从P的第2个元素开始到最后一个，让Pi通过与Pj交换 (j >= i)，得到了n-1个排列。

对于每个位置i，可以将Pi设为数组P中的任意元素，则所有n!种情况中只有一种情况是所有元素都唯一的。

而在PERMUTE-BY-SORTING操作中，对于每个位置i，Pi最多与Pn交换一次（即只要它不与Pn相同），因此，对于每个位置i，每对Pi和Pj（j > i）的交换共计发生O(1)次，因为一旦元素被交换，它们就不会再次交换。

因此，所有n!种可能的排列中，所有元素都唯一的排列数量是PERMUTE-BY-SORTING操作后的排列数量的较小值，即n!和每对Pi和Pj的交换次数的积的较小值。通过求解得出：

$$ Pr[\\text所有元素都唯一] \\geq 1 - \\frac1n! \\ \\geq 1 - \\frac1e \\ \\geq 1 - \\frac1n $$

因此，所有元素都唯一的概率至少是1-1/n，证毕。

公众号：福大大架构师每日一题

文心一言 VS 讯飞星火 VS chatgpt （25）-- 算法导论4.2 7题

七、设计算法，仅使用三次实数乘法即可完成复数 a+bi和c+di 相乘。算法需接收a、b、c和d 为输入，分别生成实部 ac-bd 和虚部ad+bc。

文心一言：

可以使用如下算法来计算复数 a+bi 和 c+di 的积，且只需进行三次实数乘法：

1.将 a 和 b 相乘，得到 ab；

2.将 c 和 d 相乘，得到 cd；

3.将 ab + cd 赋值给 ac - bd；

4.将 ab - cd 赋值给 ad + bc。

这样，就可以得到复数 a+bi 和 c+di 的积，且只需进行三次实数乘法。

讯飞星火：

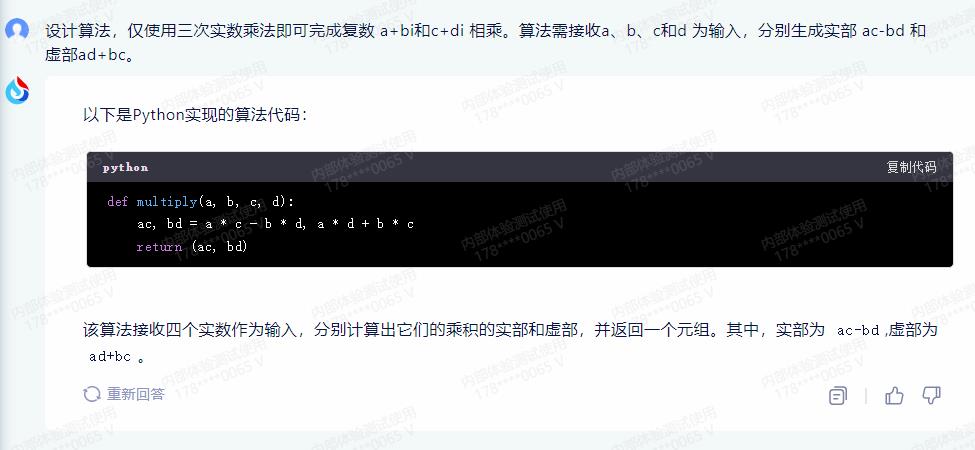
以下是Python实现的算法代码：

def multiply(a, b, c, d):
    ac, bd = a * c - b * d, a * d + b * c
    return (ac, bd)

该算法接收四个实数作为输入，分别计算出它们的乘积的实部和虚部，并返回一个元组。其中，实部为 ac-bd,虚部为 ad+bc。

华为盘古：

chatglm：

以下是一种基于三次实数乘法的复数乘法算法：

1.将两个复数 a+bi 和 c+di 分别转换为它们的实部和虚部，即实部 a+bi 和虚部 c-di。

2.计算两个实数的乘积，即 ac - bd。

3.将乘积的虚部为零，即 (ac - bd)i = aic - bid + (ac + bd)i^2。

4.计算两个虚数的乘积，即 aic + bid。

5.将乘积的实部为零，即 (aic + bid)i = ac + bd - (ac - bd)i^2。

6.最终结果为实部 ac-bd 和虚部 ad+bc。

该算法使用了三次实数乘法，因此被称为三次乘法算法。这个算法的时间复杂度为 O(n)，其中 n 是两个复数的数量。在实践中，由于复数的乘法需要进行两次实数乘法和一次虚数乘法，因此三次乘法算法的时间复杂度是略高于普通复数乘法的。但是，由于该算法的实现相对简单，而且对于某些应用场景，复数的乘法需要尽可能少地使用实数乘法，因此它仍然是一种有效的解决方案。

chatgpt：

为了仅使用三次实数乘法即可完成复数相乘，我们可以使用如下的公式：

ac-bd = (a+b)(c+d) - ac - bd
ad+bc = (a-b)(c-d) + ac + bd

这些公式基于以下思想：将两个复数相乘得到一个新的复数，其中第一项是它们的实部之积加上虚部之积的相反数，第二项是它们的虚部之积加上实部之积。我们可以通过对这些项进行重新排列和组合，将乘法的次数减少到三次。

具体地，假设要计算的两个复数为 a+bi 和 c+di，我们可以按照以下步骤进行计算：

1.计算 (a+b)(c+d)，并将结果存储在变量 re 中。

2.计算 ac，将其存储在变量 ac 中。

3.计算 bd，将其存储在变量 bd 中。

4.计算 (a-b)(c-d)，将其存储在变量 im 中。

5.将 ac 和 bd 的差值（即 ac-bd）存储在变量 real 中。

6 将 im 和 re 的和（即 ad+bc）存储在变量 imag 中。

最终的结果就是复数 real+imag*i。

注意，这种方法虽然仅使用了三次实数乘法，但需要进行多次实数加法和减法。因此，如果我们只关注乘法的次数，这种方法并不是最优的。

公众号：福大大架构师每日一题