算法学习day23二叉树part09-538108669
Posted lipin
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了算法学习day23二叉树part09-538108669相关的知识,希望对你有一定的参考价值。
package LeetCode.Treepart09; public class ConvertBSTGreaterTree_538 int sum; public TreeNode convertBST(TreeNode root) sum = 0; convertBST1(root); return root; // 按右中左顺序遍历,累加即可 public void convertBST1(TreeNode root) if (root == null) return; convertBST1(root.right); sum += root.val; root.val = sum; convertBST1(root.left);
package LeetCode.Treepart09; public class ConvertSortedArrayBinarySearchTree_108 public TreeNode sortedArrayToBST(int[] nums) return sortedArrayToBST(nums, 0, nums.length); public TreeNode sortedArrayToBST(int[] nums, int left, int right) if (left >= right) return null; if (right - left == 1) return new TreeNode(nums[left]); int mid = left + (right - left) / 2; TreeNode root = new TreeNode(nums[mid]); root.left = sortedArrayToBST(nums, left, mid); root.right = sortedArrayToBST(nums, mid + 1, right); return root;
package LeetCode.Treepart09; public class TrimBinarySearchTree_669 public TreeNode trimBST(TreeNode root, int low, int high) if (root == null) return null; if (root.val < low) return trimBST(root.right, low, high); if (root.val > high) return trimBST(root.left, low, high); // root在[low,high]范围内 root.left = trimBST(root.left, low, high); root.right = trimBST(root.right, low, high); return root;
数据结构与算法(Python)——常见数据结构Part4(二叉树)
写在前面
在上一节part3我们熟悉队列结构,本节将熟悉应用广泛的树结构。我们的目的是快速了解他们,对于它们涉及到的复杂的数据结构和算法,在这里并不全部展开,留在后期详述。
1. 树
1.1 树的直观感受
树是一个广泛应用的数据结构,即使未开始学习这个数据结构,我们在生活或者计算机中已经和它打交道好久了。首先让我们看几个树形的应用例子(图片来自What is the real life application of tree data structures?):
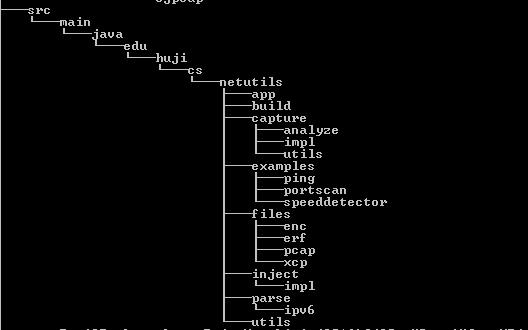
这里显示的是Windows系统下文件夹的目录结构,从src目录开始,整个目录结构构成一棵树(使用Windows命令tree可以查看文件目录结构)。
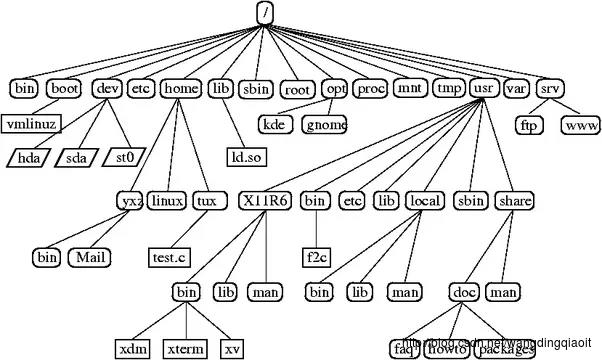
上图展现的是Linux文件系统构成的一棵树。
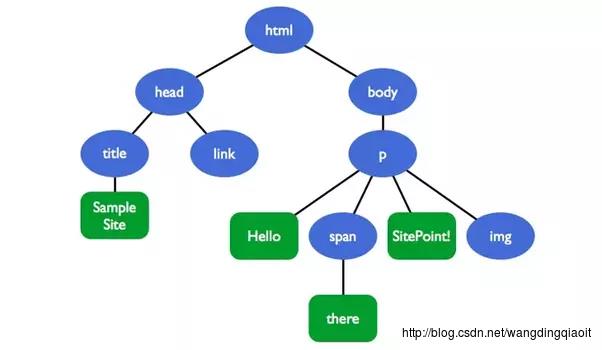
上图图展现的是HTML文档树,文档结点html及其下的其他结点构成了一棵树结构。
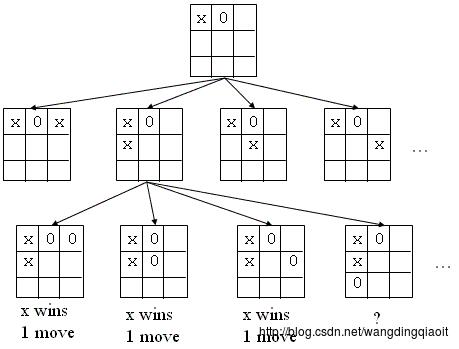
上图展示的是井字棋游戏中,人机对战时,机器从当前棋局状态推算出的下一状态构成的树形结构。
例子还有更多,通过上面的例子,我们已经对树形结构有了一个直观感受。下面我们看下计算中如何定义这个数据结构。
1.2 树的定义
在数据结构中,树被定义为这样一种结构:
- 在树中有一个特殊的结点,称作根结点(Root Node),他没有父结点或者称为前驱结点(predecessor)。
- 在树中出了根以外,每个结点都有一个父结点。
- 树中所有结点有0个后者多个后继结点(successors)。
需要注意的是树与之前学习的数组、链表、栈以及队列不同,它不是一种线性结构,而是一种层次结构(hierarchical structure )。
数据结构中的树,抽象表示为(图片来自DATA STRUCTURES-TREE):
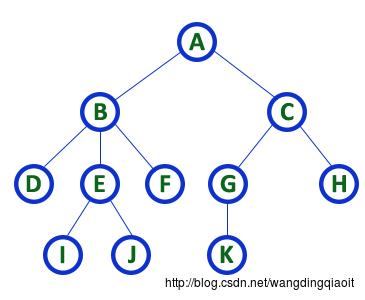
1.3 树相关的术语
了解树相关的术语对于后续学习很有必要,涉及到的术语包括下列内容(术语部分图片均来自DATA STRUCTURES-TREE)。
1) 根结点(Root)、孩子结点(Child)、父结点(Parent)
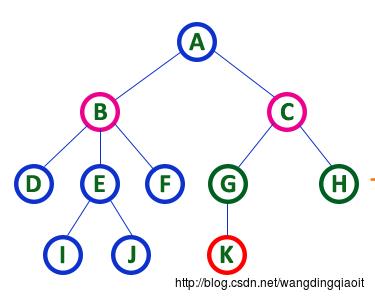
在上面的图中A结点称之为树的根结点,它是树形开始的起点;在树中一个结点的后继称之为这个结点的孩子结点,同时这个结点本身称之为它的孩子结点的父结点,例如图中根结点A有两个孩子结点B和C,B和C有一个共同的父结点A。结点K的父结点是G,同时G的父结点是C,可以看出这种层次关系。
2) 兄弟结点(Siblings)
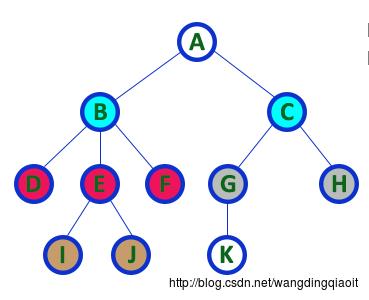
同一个父结点的孩子结点之间的关系称之为兄弟结点,例如杀那个图中D、E、F结点称之为兄弟结点,它们共同的父结点为B;G和H结点也称之为兄弟结点,它们共同的父结点为C。
3) 叶子结点(Leaf node)、 内部和外部结点(Internal and external Nodes)
至少有一个孩子结点的结点称之为内部结点(Internal nodes),一个孩子结点都没有的结点称之为孩子结点(Leaf node),也称之为外部结点(External node)或者终端结点(Terminal Node)。
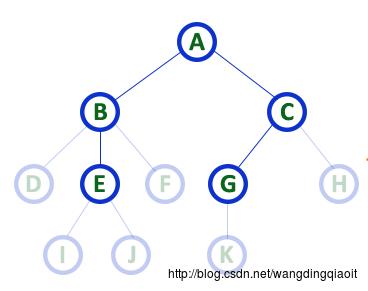
上面的图中亮色显式的都是内部结点,暗色显式的都是叶子结点。
4) 边(Edge)
边是连接两个结点的这条链接,如下图所示:
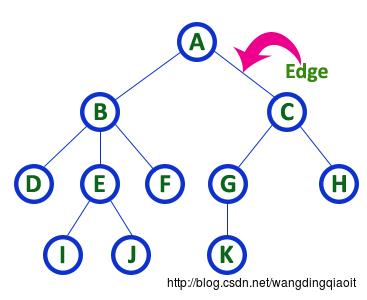
5) 入度(In Degree)和出度(Out Degree)
树中指向一个结点的边的数目称之为结点的入度,从一个结点指出的边的数目称之为结点的出度。根结点的入度总是为0,叶子结点的出度总是为0。
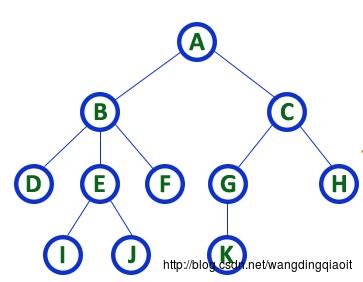
图中A结点的入度为0,出度为2;B结点的入度为1,出度为3;F结点的入度为1,出度为0。
注意,很多教材或者网站,在使用这个概念时并没有区分入度和出度,将出度,也就是结点拥有的子树数量称之为结点的度。
6) 层次(Level)
在树中根结点作为开始层,一般记为0,根结点的孩子结点记为层次1,依次类推,下一层记为2,…。注意某些情形下,根结点层次也可能记为从1开始。
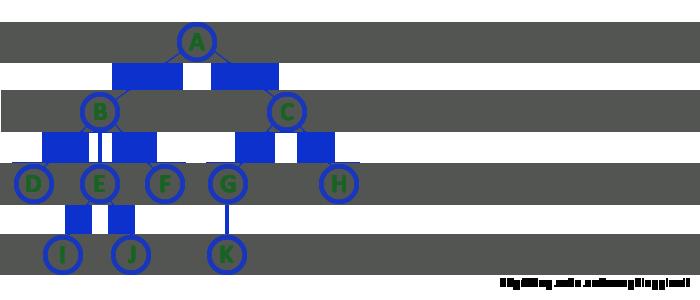
7) 高度(Height)
结点的高度定义为从叶子结点到这个结点的最长路径中边的数量。叶子结点的高度记为0。树的高度定义为根结点的高度。
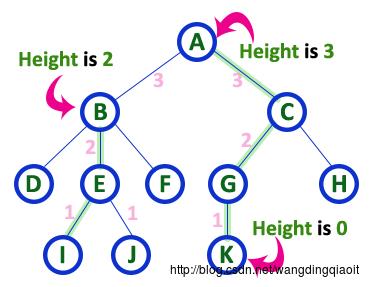
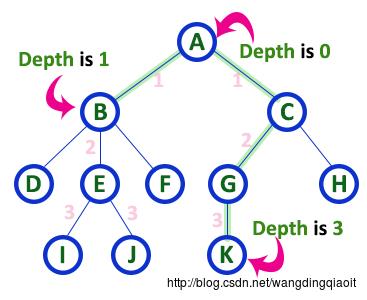
8) 深度(Depth)
树中从根结点到指定结点的路径上边的数量称为这个指定结点的深度。根结点的深度定义为0。一棵树的深度定义为从根结点到叶子结点的所有深度中的最大值。
9) 路径(Path)
树中从一个结点到另一个结点的所有边和结点称之为路径,路径的长度为其中结点的数量。
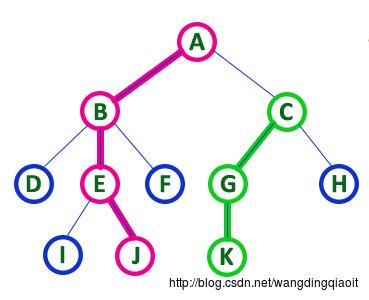
例如上图中,结点A和J之间路径为: A-B-E-J,长度为4。
10) 子树(Subtree)
在树中,当前结点的孩子结点及孩子结点的后继构成的树,称之为当前结点的子树。这个概念是递归的。
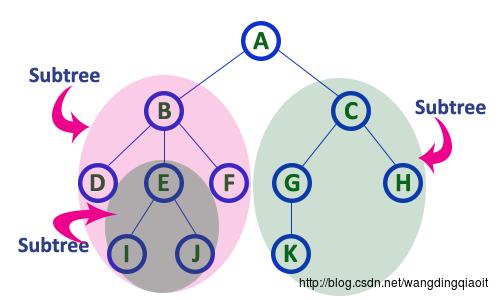
上面的图中结点A有两个子树,结点B有3个子树。
1.4 树的种类
树是数据结构学科中广泛应用,有着多个变种的重要数据结构。其中既有简单的二叉树结构,也包括AVL(一种自平衡的二叉搜索树)、RBT(红黑树)、BTree(一种允许有多个孩子结点的二叉搜索树)等复杂的数据结构,完整的列表可以查看wiki-tree。
在常见数据结构部分,本节我们重点熟悉二叉树(binary trees)、二叉搜索树( binary search trees )、堆(Heap)三种类型的树,对于其他更为复杂的数据结构,我们将留在高级数据结构部分学习。
2. 二叉树
二叉树是每个结点最多有两个孩子的树,是一种常见的树形。例如下图所示为一个二叉树:
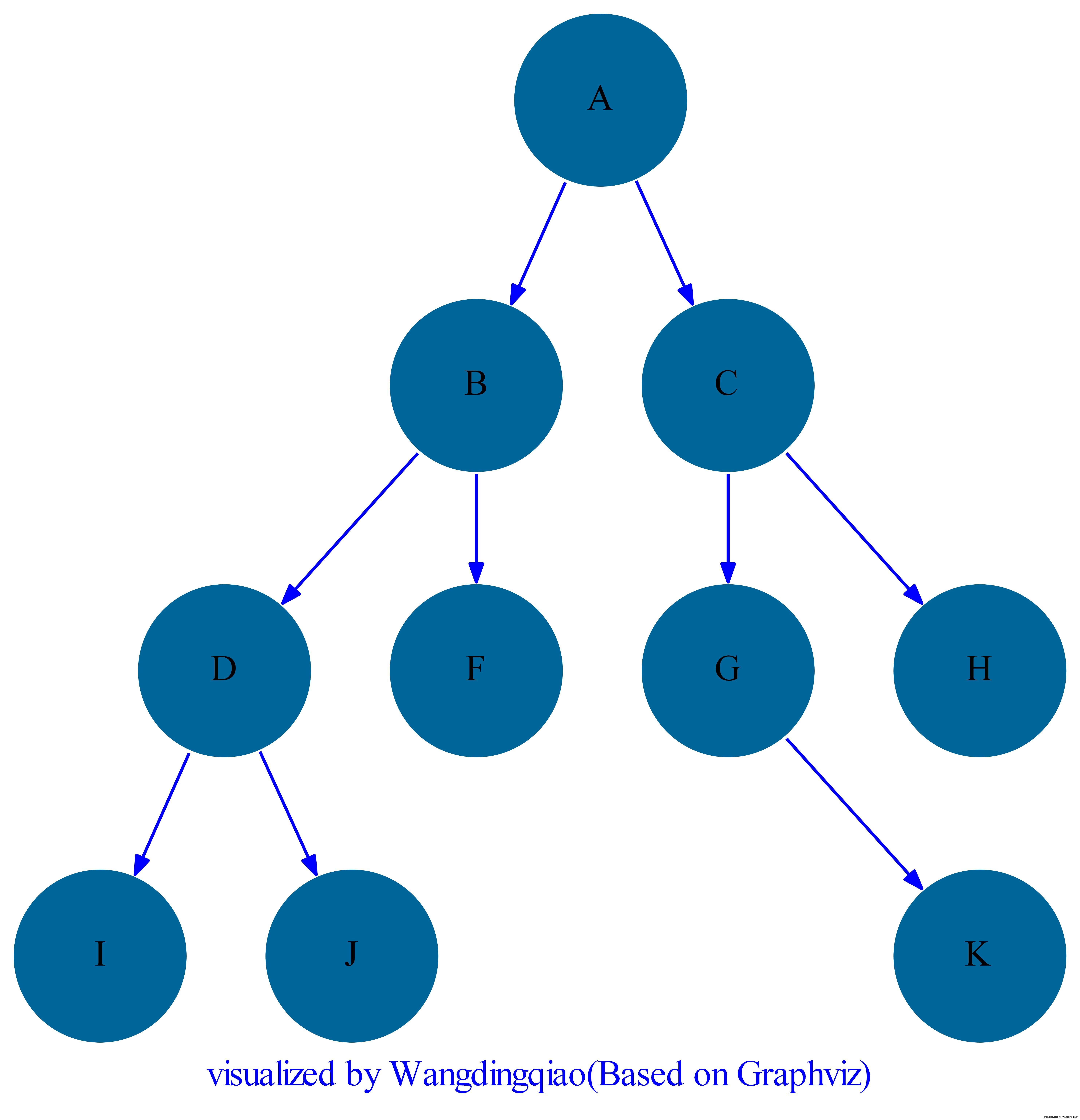
2.1 二叉树的性质
了解二叉树的性质,对于分析二叉树形态、算法复杂度很有帮助,下面简述几个重要性质,参考自二叉树性质。
1) 性质1 二叉树第i层上的结点数目最多为
2i−1(i≥1)
2
i
−
1
(
i
≥
1
)
第一层为根结点,i=1,此时满足上述公式;可以通过归纳法证明上述公式,证明留给读者自行证明。
2) 性质2 深度为k的二叉树至多有
2k−1(k≥1)
2
k
−
1
(
k
≥
1
)
个结点
由性质1, 求和可得:
20+21+…+2k−1=2k−1
2
0
+
2
1
+
…
+
2
k
−
1
=
2
k
−
1
3) 性质3 在任意-棵二叉树中,若终端结点的个数为 n0 n 0 ,度为2的结点数为 n2 n 2 ,则 no=n2+1 n o = n 2 + 1 。
记树中结点总数为n,则有:
n=n0+n1+n2(1)
(1)
n
=
n
0
+
n
1
+
n
2
另一方面,除了根结点外,每个结点都是有父结点的,
n0
n
0
不产生子结点,
n1
n
1
结点产生一个子结点,
n2
n
2
产生两个孩子结点,则有:
n−1=n1+2n2(2)
(2)
n
−
1
=
n
1
+
2
n
2
由式(1)和式(2)得出: no=n2+1 n o = n 2 + 1
二叉树中,如果一棵深度为 k k 且有个结点的二叉树则称之为满二叉树(Full Binary Tree),满二叉树有两个特点:
(1) 每一层上的结点数都达到最大值。即对给定的高度,它是具有最多结点数的二叉树。
(2) 满二叉树中不存在度数为1的结点,每个分支结点均有两棵高度相同的子树,且树叶都在最下一层上。
对满二叉树的结点从上到下,从左到右编号为 1..n 1.. n ,可以引出完全二叉树的概念。如果一个深度为 k k ,有个结点的二叉树,当且仅当其每个结点都与深度为k的满二叉树中编号为1到n的结点一一对应时,称之为完全二叉树(Complete Binary Tree)。完全二叉树的特点:
(1) 叶子结点只可能出现在层次最大的两层
(2) 对于任一结点,若其右分支下子孙的最大层次为 l l ,则其左分支下子孙的最大层次为或者 l+1 l + 1 。
(3) 满二叉树是完全二叉树,完全二叉树不一定是满二叉树。
(4) 在满二叉树的最下一层上,从最右边开始连续删去若干结点后得到的二叉树仍然是一棵完全二叉树。
(5) 在完全二叉树中,若某个结点没有左孩子,则它一定没有右孩子,即该结点必是叶结点。
4) 性质4:具有n个结点的完全二叉树的深度为
floor(logn)+1
f
l
o
o
r
(
l
o
g
n
)
+
1
.
证明: 设所求深度为
k
k
,深度为的完全二叉树则
k−1
k
−
1
层以前构成一棵满二叉树,节点个数为
以上是关于算法学习day23二叉树part09-538108669的主要内容,如果未能解决你的问题,请参考以下文章