洛谷 P6003 总结
Posted xhr0817-blog
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了洛谷 P6003 总结相关的知识,希望对你有一定的参考价值。
题目:洛谷 P6003
题意
-
有一个人欠了别人 \\(n\\) 单位牛奶,每一天他会还 \\(y = \\max(m, \\fracn - gx)\\) 单位,\\(g\\) 为之前还的牛奶,请求出最大的 \\(x\\) 使得这个人在 \\(k\\) 天后能换至少 \\(k\\) 单位牛奶。
-
\\(1 \\le n, m, k \\le 10^12, km < n\\)。
思路
暴力
首先这个题有单调性,若 \\(x\\) 能满足要求,那么 \\(x-1\\) 也行。所以可以二分 \\(x\\),在模拟 \\(k\\) 天的情况,判断即可。
正解
-
可以发现这在很多天里,\\(y\\) 是相同的,如果把这些相同的合并起来,就可以降低很多的复杂度。但是怎么知道现在有多少个相同的呢,我们需要先找到需要达到要求的最小 \\(n\\),也就是 \\(xy\\),那么当前的 \\(n - g\\) 要经历多少次才会 $ < xy$ 呢,答案是 \\(\\lceil \\fracn - g - xyy \\rceil\\),所以这就达到了合并相同的 \\(y\\) 的效果。
-
最后判断需要的天数和 \\(k\\) 的大小关系即可,注意每天至少给 \\(m\\) 单位的细节即可。
-
但是问题来了,这能过吗,可以发现每个 \\(y\\) 都不一样,所以最极端的情况是 \\(y = 1, 2, 3, 4, \\dots\\),\\(y\\) 的种数只有 \\(\\sqrtn\\) 级别,可以通过此题。
时间复杂度
暴力
- 二分:\\(O(\\log n)\\)。
- 模拟:\\(O(k)\\)。
- 总时间复杂度:\\(O(k \\log n)\\)。
正解
- 二分:\\(O(\\log n)\\)。
- \\(y\\) 最多 \\(\\sqrtn\\) 种取值,\\(O(\\sqrtn)\\)。
- 总时间复杂度:\\(O(\\log n \\cdot \\sqrtn)\\)。
using ll = long long;
ll n, k, m;
bool Check(ll x)
if (n / x < m)
return 0;
ll w = x * m, _n = n, c = 0;
while (_n > w)
ll q = _n / x, t = x * q; // 注明一下 q 是思路中的 y
ll s = max(1LL, (_n - t + q - 1) / q); // 增加的天数
_n -= s * q, c += s; // _n %= q
return (c + (_n + m - 1) / m <= k);
ll F() // 二分答案
ll l = 1, r = n;
while(l < r)
ll mid = (l + r + 1) >> 1;
if (Check(mid))
l = mid;
else
r = mid - 1;
return l;
int main()
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> k >> m;
cout << F();
return 0;
洛谷 P3367- 并查集(Java模板)
概论
定义:
并查集是一种树型的数据结构,用于处理一些不相交集合的合并及查询问题(即所谓的并、查)。
比如,我们可以用并查集来判断一个森林中有几棵树、某个节点是否属于某棵树等。
主要构成:
并查集主要由一个整型数组pre[]和两个函数find()、join()构成。
数组 pre[] 记录了每个点的前驱节点(父结点)是谁,函数 find(x) 用于查找指定节点 x 属于哪个集合,函数 join(x,y) 用于合并两个节点 x 和 y 。
加权标记法
路径压缩算法:加权标记法
主要思路:
加权标记法需要将树中所有节点都增设一个权值,用以表示该节点所在树中的高度(比如用rank[x]=3表示 x 节点所在树的高度为3)。
这样,在合并操作的时候就能通过这个权值的大小来决定谁做父结点。避免构造出来的树是连续一直向上的,便于优化查找效率。
举个例子,我们对以A,F为代表元的集合进行合并操作(如下图所示):
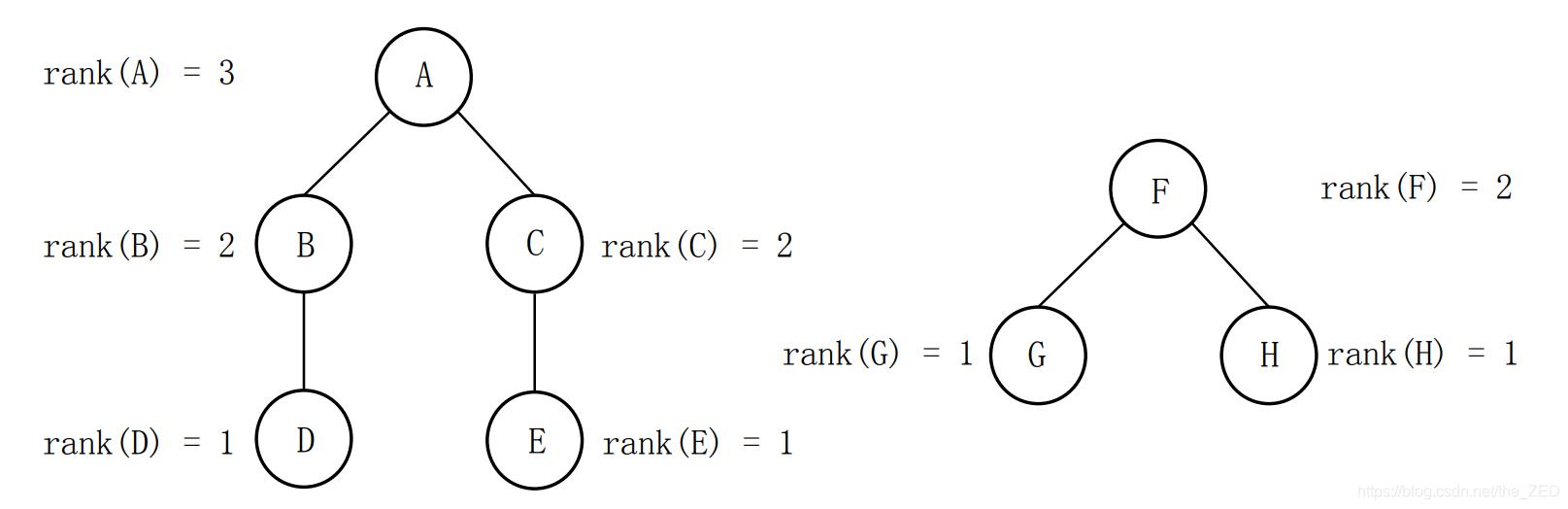
由于 rank(A) > rank(F) ,因此令 pre[F]= A。合并后的图形如下图所示:
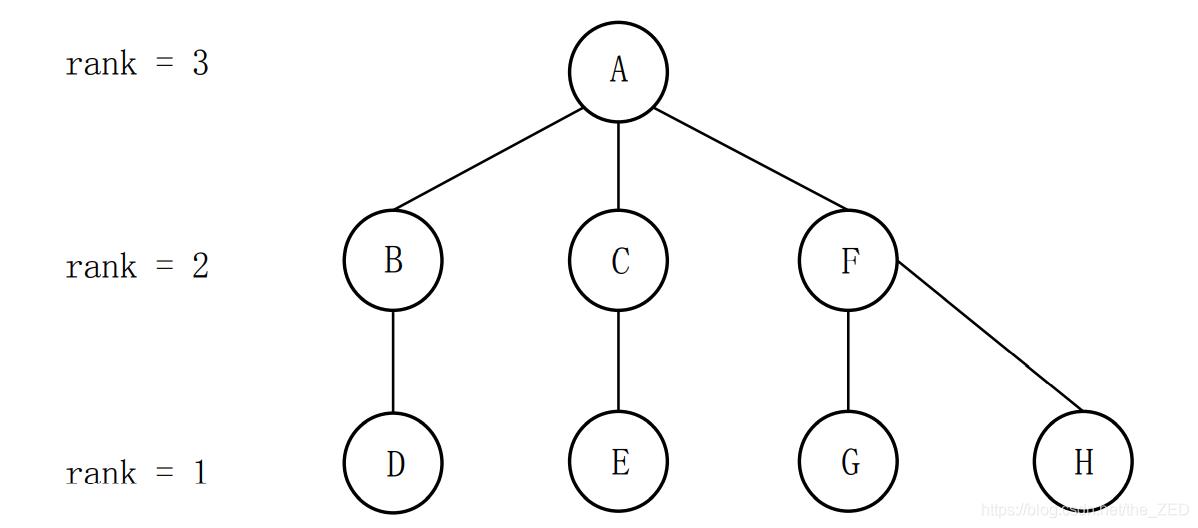
可以看出,合并前两个树的最大高度为3,合并后依然是3,这也就达到了我们的目的。但如果令pre[A]= F,那么就会使得合并后的树的总高度增加。
我们常说,鱼和熊掌不可兼得,同理,时间复杂度和空间复杂度也很难兼得。由于给每个节点都增加了一个权值来标记其在树中的高度,这也就意味着需要额外的数据结构来存放权重信息,所以这将导致额外的空间开销。
总结
- 用集合中的某个元素来代表这个集合,则该元素称为此集合的代表元;
- 一个集合内的所有元素组织成以代表元为根的树形结构;
- 对于每一个元素 x,pre[x] 存放 x 在树形结构中的父亲节点(如果 x 是根节点,则令pre[x] = x);
- 对于查找操作,假设需要确定 x 所在的的集合,也就是确定集合的代表元。可以沿着pre[x]不断在树形结构中向上移动,直到到达根节点。
因此,基于这样的特性,并查集的主要用途有以下两点:
- 维护无向图的连通性(判断两个点是否在同一连通块内,或增加一条边后是否会产生环);
- 用在求解最小生成树的Kruskal算法里。
一般来说,一个并查集对应三个操作:
- 初始化( Init()函数 )
- 查找函数( Find()函数 )
- 合并集合函数( Join()函数 )
P3367 并查集

输入输出样例
输入
4 7
2 1 2
1 1 2
2 1 2
1 3 4
2 1 4
1 2 3
2 1 4
输出
N
Y
N
Y
参考代码:
import java.io.*;
import java.util.Arrays;
public class Main {
static StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
public static void main(String[] args) {
int n = nextInt();
int m = nextInt();
int[] parents = new int[n+1];
int[] rank = new int[n+1];
Arrays.fill(parents, -1);
while (m-- > 0) {
int z = nextInt();
int x = nextInt();
int y = nextInt();
if (z == 1) {
union(x, y, parents, rank);
} else {
if (find(x, parents) == find(y, parents))
System.out.println("Y");
else
System.out.println("N");
}
}
}
// 判断元素是否属于同一集合,如果有公共父结点就在同一集合
public static int find(int x, int[] parents) {
int root = x;
while (parents[root] != -1) {
root = parents[root];
}
return root;
}
public static boolean union (int x, int y, int[] parents, int[] rank) {
int x_root = find(x, parents);
int y_root = find(y, parents);
if (x_root == y_root) {
return false;
} else if (rank[x_root] > rank[y_root]) {
parents[y_root] = x_root;
} else if (rank[x_root] < rank[y_root]) {
parents[x_root] = y_root;
} else {
parents[x_root] = y_root;
rank[y_root]++;
}
return true;
}
static int nextInt() {
try {
in.nextToken();
} catch (IOException e) {
e.printStackTrace();
}
return (int)in.nval;
}
}
P1551 亲戚

输入
6 5 3
1 2
1 5
3 4
5 2
1 3
1 4
2 3
5 6
输出
Yes
Yes
No
参考代码
import java.io.*;
import java.util.Arrays;
public class Main {
static StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
public static void main(String[] args) {
int n = nextInt();
int m = nextInt();
int[] parents = new int[n+1];
int[] rank = new int[n+1];
Arrays.fill(parents, -1);
int p = nextInt();
while (m-- > 0) {
int x = nextInt();
int y = nextInt();
union(x, y, parents, rank);
}
while (p-- > 0) {
int x = nextInt();
int y = nextInt();
if (find(x, parents) == find(y, parents))
System.out.println("Yes");
else
System.out.println("No");
}
}
// 判断元素是否属于同一集合,如果有公共父结点就在同一集合
public static int find(int x, int[] parents) {
int root = x;
while (parents[root] != -1) {
root = parents[root];
}
return root;
}
public static boolean union (int x, int y, int[] parents, int[] rank) {
int x_root = find(x, parents);
int y_root = find(y, parents);
if (x_root == y_root) {
return false;
} else if (rank[x_root] > rank[y_root]) {
parents[y_root] = x_root;
} else if (rank[x_root] < rank[y_root]) {
parents[x_root] = y_root;
} else {
parents[x_root] = y_root;
rank[y_root]++;
}
return true;
}
static int nextInt() {
try {
in.nextToken();
} catch (IOException e) {
e.printStackTrace();
}
return (int)in.nval;
}
}

加油!
感谢!
努力!
以上是关于洛谷 P6003 总结的主要内容,如果未能解决你的问题,请参考以下文章