最短路与生成树算法

Posted 2023-06-02 MichaelWong - 二两碘酊

写在前面

最短路部分的代码还是 3 月的，奇丑无比，大家见谅……

---

最短路

单源最短路径

首先我们介绍一些基本概念。

由于是单源最短路，我们定义一个起点 \\(s\\)，\\(dis_u\\) 表示起点 \\(s\\) 到节点 \\(u\\) 的最短路长度。

一般来讲，对于一条为 \\(w\\) 的边 \\(u \\to v\\)，如果目前的最短路是正确的，都应该满足：

\\[dis_u+w \\geq dis_v \\]

我们称之为 三角形不等式。

对于不满足三角形不等式的，我们就要更新最短路了：

一条边权为 \\(w\\) 的边 \\(u \\to v\\)，如果满足 \\(dis_u+w<dis_v\\)，即可用 \\(dis_u+w\\) 更新 \\(dis_v\\)。

这个更新的过程叫做 松弛。

松弛是所有最短路算法的基本操作，我们这里讲的是单源，其实多源也是一样的道理。

Dijkstra

首先是我们的老朋友迪科斯彻。

将有项带权图 \\(G=(V,E)\\) 的点集 \\(V\\) 分为两个集合：\\(S\\) 和 \\(T\\)，\\(S\\) 中的点已确定最短路径长度，（即 \\(dis_u\\) 已更新。起初， \\(S\\) 中仅包含源点 \\(s\\)，除 \\(dis_s=0\\) 外 \\(dis\\) 初值皆为 \\(+\\infty\\)。）\\(T\\) 中的点没有确定。

迪科斯彻采用了 贪心 的思想，在 \\(S\\) 中选择 \\(dis_u\\) 最小的节点 \\(u\\)，对 \\(u\\) 的所有出边进行松弛。

可以证明，由于贪心，每个节点的 \\(dis\\) 只会更新一次，所以可以对已经松弛所有出边的节点 \\(u\\) 打标，这个松弛操作 只进行一次 即可。

当然了，最原始的 Dijkstra 时间复杂度还是太假。由于我们只选取最短的一条特殊路径进行松弛，其实可以采用伟大的标准模板库 STL 中的 priority_queue 解决这个问题。

解决之后，我们最坏对 \\(m\\) 条边进行松弛，优先队列单次操作复杂度 \\(O(\\log n)\\)，所以总复杂度 \\(O(m \\log n)\\)，非常优秀。

接下来是模板题 单源最短路径（标准版） 的 \\(Code\\)：

#include<bits/stdc++.h>
const int N=1e5+5;
struct Edge  int to,w;
	bool operator < (const Edge &a) const return w>a.w;
;
std::vector <Edge> E[N];//使用结构体和vector存边
int n,m,s,dis[N];
bool flag[N];
void Dijkstra(int start)

	memset(dis,0x3f,sizeof dis);
	std::priority_queue <Edge> q;
	dis[start]=0;
	q.push(start,0);
	while(!q.empty())
		int u=q.top().to;
		q.pop();
		if(flag[u])	continue;
		/*每个点仅一次作为媒介节点参与松弛。*/
		flag[u]=1;
		for(auto v:E[u])
			if(dis[u]+v.w<dis[v.to])
				dis[v.to]=dis[u]+v.w;//松弛
				q.push(v.to,dis[v.to]);//入集合S
			
		
	

int main()

	std::ios::sync_with_stdio(0);
	std::cin.tie(0);std::cout.tie(0);
	std::cin>>n>>m>>s;
	for(int i=1;i<=m;++i)
		int u,v,w;
		std::cin>>u>>v>>w;
		E[u].push_back(v,w);
	
	Dijkstra(s);
	for(int i=1;i<=n;++i)
		std::cout<<dis[i]<<" ";
	return 0;

但是呢，Dijkstra 不能用于 负环。因为在 Dijkstra 中，每一个顶点作为媒介节点参与松弛操作只有一次，所以得出的结果其实是松弛一次的结果，且无法进行判断其是否是负环。

同时，存在 负边权 的图也 不可 使用 Dijkstra。

Bellman-Ford

其实是一个非常朴素的想法，朴素到其复杂度为 \\(O(VE)\\)，本质就是对每一条边都尝试松弛。因为其复杂度过于高，实际用途已经基本废了。所以现在主要介绍的是其优化后的算法，SPFA。

SPFA

Shortest Path Faster Algorithm, AKA SPFA。

实际上，这个名字只在大陆存在。因为他实际上叫做 队列优化的 Bellman-Ford 算法。顾名思义，使用队列来优化 Bellman-Ford，本质思想还是朴素的对每个边进行松弛，而且——

\\[\\text关于 SPFA, \\textbf他死了。 \\]

（ 这个帖子 足见杀他的方法已经发展得很完备了。）

所以直接上 模板题 代码吧。

\\(Code\\)：

#include<bits/stdc++.h>
const int N=1e4+5;
int n,m,s,dis[N];
bool vis[N];
struct Edge	int to,w;;
std::vector<Edge> E[N];
void SPFA(int start)
	std::queue<int> q;
	for(int i=1;i<=n;++i)
		dis[i]=INT_MAX;
	vis[start]=1,dis[start]=0;
	q.push(start);
	while(!q.empty())
		int u=q.front();
		q.pop();
		vis[u]=0;
		for(auto v:E[u])
			if(dis[u]+v.w<dis[v.to])
				dis[v.to]=dis[u]+v.w;
				if(!vis[v.to])
					vis[v.to]=1;
					q.push(v.to);
				
			
		
	

int main()
	std::ios::sync_with_stdio(0);
	std::cin.tie(0);std::cout.tie(0);
	std::cin>>n>>m>>s;
	for(int i=1;i<=m;++i)
		int u,v,w;
		std::cin>>u>>v>>w;
		E[u].push_back(v,w);
	
	SPFA(s);
	for(int i=1;i<=n;++i)
		std::cout<<dis[i]<<" ";
	return 0;

SPFA 的复杂度一般是 \\(O(km)\\) 的，但是在一些特殊图（如网格图和链套菊花）中会退化到 \\(O(nm)\\)，所以，慎用。

最后的用武之地 - 判断负环

在 SPFA 中，一个节点最多被松弛 \\(n\\) 次。所以，我们可以记录每个节点 \\(u\\) 被松弛的次数 \\(sum_u\\)，如果出现 \\(sum_n>n\\)，就可以判定出现负环了。

---

多源最短路径 - Floyd

OK，现在我们来说一下最后的，多源最短路径。解决他的算法是 Floyd。

其实这个 Floyd 就是一个动态规划，使用邻接矩阵 \\(dis(i,j)\\) 表示从 \\(i\\) 到 \\(j\\) 的最短路径长，枚举每一个节点 \\(k\\)，判断其是否满足三角形不等式，不满足就 \\(dis(i,j) \\gets dis(i,k)+dis(k,j)\\)。

\\(Code:\\)

for(int k=1;k<=n;++k)
	for(int i=1;i<=n;++i)
    	for(int j=1;j<=n;++j)
        	dis[i][j]=std::min(dis[i][j],dis[i][k]+dis[k][j]);
		
	

Floyd 是敲着最简单的，但是 \\(O(n^3)\\) 的复杂度，所以小一点的图哪怕单源也可以凑合用，要是图很大就慎重吧。

---

生成树

本部分旨在速通，复习用，看细节的朋友可以看 catandcode 的博客。

最小生成树 - MST

性质

就是：

对于一个无向连通图 \\(G=(V,E)\\)，点集 $U \\subsetneq V $ 和 边集 \\(A=\\ u \\leftrightarrow v|u \\in U,v \\in (V-U) \\ \\subsetneq E\\)，有无向边 \\(u \\leftrightarrow v \\in A\\) 且在 \\(A\\) 中边权 \\(w_u,v\\) 最小，则这条边必然在该图 \\(G\\) 的一棵最小生成树中。

Prim

将无向连通图 \\(G=(V,E)\\) 分为两个集合：已处理 \\(A\\) 和未处理 \\(B\\)。处理的过程如下：

1. 将一个节点 \\(u\\) 放入集合 \\(A\\)；
2. 在边集 \\(C=\\ i \\leftrightarrow j | i \\in A,j \\in B\\\\subset E\\) 寻找最小的一条边，将这条边纳入最小生成树；
3. 重复第 2 步，直至 \\(B= \\varnothing\\)。

Prim 更适合 稠密图。

\\(\\textCode - with Prim by Adjacency List, 1.19 s \\text without O2\\)

#include<bits/stdc++.h>
const int MAXN=5005,inf=0x3f3f3f3f;
int n,m,sp[MAXN],dis[MAXN][MAXN];
bool flag[MAXN];
int prim() 
    int ans=0,tot=0; sp[0]=inf,flag[1]=1;
    for(int i=2;i<=n;++i) sp[i]=dis[1][i];
    for(int i=1;i<n;++i) 
    	int tmp=0;
        for(int v=1;v<=n;++v) if(!flag[v] && sp[v]<sp[tmp]) tmp=v;
        if(!tmp) break;
        ans+=sp[tmp],flag[tmp]=1,++tot;
        for(int l=1;l<=n;++l) if(!flag[l] && dis[tmp][l]<sp[l]) sp[l]=dis[tmp][l];
    
    return tot==n-1?ans:-1;

int main() 
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr); std::cout.tie(nullptr);
    std::cin>>n>>m; memset(dis,0x3f,sizeof dis);
    for(int i=1,u,v,w;i<=m;++i)  std::cin>>u>>v>>w; dis[u][v]=dis[v][u]=std::min(dis[u][v],w); 
    int ans=prim();
	if(~ans) std::cout<<ans<<\'\\n\';
	else std::cout<<"orz\\n";
	return 0;

下面是前向星 prim. 与邻接矩阵不同的是，邻接矩阵需要判断重边，\\(sp\\) 就可以直接赋值；而前向星不需要判断重边，所以 \\(sp\\) 需要取所有边中的最小值。

\\(\\textCode - with Prim by Forward Star, 474 ms \\text without O2\\)

#include<bits/stdc++.h>
#define ll long long
#define ld long double
#define fsp(x) std::fixed<<std::setprecision(x)
#define forE(u) for(int p=head[u],v=E[p].to;p;p=E[p].next,v=E[p].to)
const int N=5005,M=2e5+5,inf=0x3f3f3f3f;
int cnt,head[N];
struct edge  int to,next,w;  E[M<<1];
void add(int u,int v,int w)  E[++cnt].to=v,E[cnt].w=w,E[cnt].next=head[u],head[u]=cnt; 
int n,m,sp[N];
bool flag[N];
int prim() 
	memset(sp,0x3f,sizeof sp);
	int ans=0,tot=0; flag[1]=1;
	forE(1) sp[v]=std::min(sp[v],E[p].w);
	for(int i=1;i<=n;++i) 
		int tmp=0;
		for(int v=1;v<=n;++v) if(!flag[v] && sp[v]<sp[tmp]) tmp=v;
		if(sp[tmp]==inf) break;
		ans+=sp[tmp],flag[tmp]=1,++tot;
		forE(tmp) sp[v]=std::min(sp[v],E[p].w);
	
	return tot==n-1?ans:-1;

int main() 
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr); std::cout.tie(nullptr);
	std::cin>>n>>m;
	for(int i=1,u,v,w;i<=m;++i)  std::cin>>u>>v>>w; add(u,v,w),add(v,u,w); 
	int ans=prim();
	if(~ans) std::cout<<ans<<\'\\n\';
	else std::cout<<"orz\\n";
	return 0;

Kruskal

基于贪心的思想，使用并查集维护状态（一个集合一棵树），将所有边从小到大排序后遍历，如果两个点不在同一棵树上，则将该边纳入 MST，合并这条边连通的两个端点的集合。

Kruskal 更适合 稀疏图。

\\(\\textCode - with Kruskal by Forward Star and Disjoint Set Union, 230 ms \\text without O2\\)

#include<bits/stdc++.h>
#define ll long long
#define ld long double
const int N=5005,M=2e5+5;
struct edge  int from,to,w;  E[M];
void add(int u,int v,int w,int ord)  E[ord].from=u,E[ord].to=v,E[ord].w=w; 
int n,m,fa[N];
void init()  for(int i=1;i<=n;++i) fa[i]=i; 
int get(int x)  return fa[x]==x?x:fa[x]=get(fa[x]); 
void merge(int x,int y)  fa[get(y)]=get(x); 
int kruskal() 
	init();
	std::sort(E+1,E+m+1,[](const edge &a,const edge &b) return a.w<b.w; );
	int ans=0,tot=0; edge *it=E;
	while(++it<E+m+1) 
		if(get(it->from)==get(it->to)) continue;
		ans+=it->w,merge(it->from,it->to),tot++;
		if(tot==n-1) break;
	
	return tot==n-1?ans:-1;

int main() 
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr); std::cout.tie(nullptr);
	std::cin>>n>>m;
	for(int i=1,u,v,w;i<=m;++i)  std::cin>>u>>v>>w; add(u,v,w,i); 
	int ans=kruskal();
	if(~ans) std::cout<<ans<<\'\\n\';
	else std::cout<<"orz\\n";
	return 0;

最大生成树

有什么好说的呢…算法相同，其实就只把排序/比较大小反过来罢了。

大概就是这样。

次小生成树

分为 非严格次小生成树 和 严格最小生成树。差别其实就是是否有边权和 严格大于 MST 边权和。

简单来说，在找到 MST 后枚举未在 \\(E_MST\\) 中的边 \\(u \\to v\\)，然后断开 \\(u\\) 到 \\(v\\) 的路径上的最长边，将当前边加入边集，寻找最小的边权和即可。对于严格最小生成树，考虑到最长边边权可能与当前边权相同，还要同时记录 次大值。

严格最小生成树的伪代码如下：

\\[\\beginarrayll 1 & \\textbfInput. \\textThe number of vertexs and edges of the undigraph G, \\\\ & \\textthe edges of the graph e, \\textwhich element in e \\text is (u,v,w) \\\\ & \\textdenoting that there is an edge between u \\text and v \\text weighted w . \\\\ 2 & \\textbfOutput. \\textThe sum of the weights of the edges in the set of edges E_S.\\\\ & \\textOr formally, \\sum_e \\in E_S w_e.\\\\ 3 & \\textbfMethod. \\\\ 4 & \\textinitialize the disjoint set union \\\\ 5 & mstlen \\gets 0,E_M \\gets \\varnothing \\\\ 6 & \\textsort e \\text into nondecreasing order by weight w \\\\ 7 & \\textbffor \\texteach (u,v,w) \\text ordered i \\text in the sorted e\\\\ 8 & \\qquad \\textbfif u \\text and v \\text are not connected in the disjoint set union \\\\ 9 & \\qquad \\qquad mstlen \\gets mstlen + w\\\\ 10 & \\qquad \\qquad \\textmerge u \\text and v \\text in the disjoint set union\\\\ 11 & \\qquad \\qquad E_M \\gets E_M \\bigcup \\(u,v,w)\\ \\\\ 12 & dfs(u \\gets 1,fa \\gets 0) \\text to initialize the binary-lifting funtions \\\\ 13 & ans \\gets \\infty \\\\ 14 & \\textbffor \\texteach (u,v,w) \\text which is not in E_M \\text and satisfies the limit u \\neq v \\\\ 15 & \\qquad lca \\gets \\operatornameLCA(u,v),tmp_1 \\gets - \\infty, tmp_2 \\gets - \\infty \\\\ 16 & \\qquad tmp_1 \\gets \\textthe maximum weight on the path from lca \\text to u \\\\ 17 & \\qquad \\textbfif tmp_1 = w \\\\ 18 & \\qquad \\qquad tmp_1 \\gets \\textthe sub-maximum weight on the path from lca \\text to u \\\\ 19 & \\qquad tmp_2 \\gets \\textthe maximum weight on the path from lca \\text to v \\\\ 20 & \\qquad \\textbfif tmp_2 = w \\\\ 21 & \\qquad \\qquad tmp_2 \\gets \\textthe sub-maximum weight on the path from lca \\text to v \\\\ 22 & \\qquad \\textbfif tmp_1 = tmp_2 = - \\infty \\\\ 23 & \\qquad \\qquad \\textbfcontinue \\\\ 24 & \\qquad ans \\gets \\min \\left( ans, mstlen- \\max(tmp_1,tmp_2)+w \\right) \\\\ 25 & \\textbfreturn ans \\endarray \\]

放一段优美的 \\(code\\)：

#include<bits/stdc++.h>
#define ll long long
#define ld long double
#define forE(u) for(int p=head[u],v=E[p].to;p;p=E[p].next,v=E[p].to)
const int N=1e5+5,M=3e5+5;
const ll inf=1e18+9;
int n,m;
// set of edges module
bool used[M];
struct pr  int from,to; ll w;  prE[M];
inline void add(int u,int v,ll w,int id)  prE[id].from=u,prE[id].to=v,prE[id].w=w; 
int cnt,head[N];
struct edge  int to,next; ll w;  E[N<<1];
inline void addedge(int u,int v,ll w)  E[++cnt].to=v,E[cnt].w=w,E[cnt].next=head[u],head[u]=cnt; 
// DSU module
int fa[N];
void init()  for(int i=1;i<=n;++i) fa[i]=i; 
int get(int x)  return fa[x]==x?x:fa[x]=get(fa[x]); 
void merge(int x,int y)  fa[get(y)]=get(x); 
// kruskal module
ll kruskal() 
	init();
	std::sort(prE+1,prE+m+1,[](const pr &a,const pr &b) return a.w<b.w; );
	int tot=0; ll ans=0; pr *it=prE;
	while(tot<n-1) 
		it++; if(it==prE+m+1) break;
		if(get(it->from)==get(it->to)) continue;
		ans+=it->w,used[it-prE]=1,merge(it->from,it->to),tot++;
		addedge(it->from,it->to,it->w),addedge(it->to,it->from,it->w);
	
	return ans;

// MST module
int dep[N],anc[22][N];
ll mx[22][N],sec[22][N];
void dfs(int u,int f) 
	dep[u]=dep[f]+1,anc[0][u]=f,sec[0][u]=-inf;
	for(int i=1;(1<<i)<=dep[u];++i) 
		anc[i][u]=anc[i-1][anc[i-1][u]];
		ll tmp[]=mx[i-1][u],mx[i-1][anc[i-1][u]],sec[i-1][u],sec[i-1][anc[i-1][u]];
		std::sort(tmp,tmp+4);
		mx[i][u]=tmp[3];
		int ptr=2;
		while(~ptr && tmp[ptr]==tmp[3]) ptr--;
		sec[i][u]=~ptr?tmp[ptr]:-inf;
	
	forE(u) if(v!=f) mx[0][v]=E[p].w,dfs(v,u);

int LCA(int u,int v) 
	if(dep[v]>dep[u]) std::swap(u,v);
	int d=dep[u]-dep[v];
	for(int i=20;~i;--i) if(d&(1<<i)) u=anc[i][u];
	if(u==v) return u;
	for(int i=20;~i;--i) if(anc[i][u]!=anc[i][v]) u=anc[i][u],v=anc[i][v];
	return anc[0][u];

ll query(int u,int v,ll w) 
	ll ans=-inf;
	if(dep[v]>dep[u]) std::swap(u,v);
	int d=dep[u]-dep[v];
	for(int i=20;~i;--i) if(d&(1<<i)) 
		if(mx[i][u]==w) ans=std::max(ans,sec[i][u]);
		else ans=std::max(ans,mx[i][u]);
		u=anc[i][u];
	
	return ans;

// beautiful main program
int main() 
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr); std::cout.tie(nullptr);
	std::cin>>n>>m;
	for(int i=1,u,v,w;i<=m;++i)  std::cin>>u>>v>>w; add(u,v,w,i); 
	ll mstlen=kruskal(),ans=inf; dfs(1,0);
	for(int i=1;i<=m;++i) 
		if(used[i] || prE[i].from==prE[i].to) continue;
		int lca=LCA(prE[i].from,prE[i].to);
		ll tmp1=query(prE[i].from,lca,prE[i].w),tmp2=query(prE[i].to,lca,prE[i].w);
		if(tmp1==-inf && tmp2==-inf) continue;
		ans=std::min(ans,mstlen-std::max(tmp1,tmp2)+prE[i].w);
	
	std::cout<<ans<<\'\\n\';
	return 0;

最小生成树(Prim,Kruskal)--最短路径(Dijkstra,Floyd)算法详解

最小生成树

Prim（普雷姆）算法

以某一个顶点开始构建生成树，每次将代价最小的新顶点纳入生成树，直到所有顶点都纳入位置。设有如下图：
从P点开始构建生成树，选择其他顶点也可

首先与P相连最小的代价（边）是学校，代价为1，将其并入：

此时与生成树相连的边有5，6，5，4，6，4，最小的代价时连渔村或者矿场，我们这里选择连矿场，选渔村的话生成的最小生成树代价不变，所以同一个图可以有多个最小生成树此时最小树生成树如图：

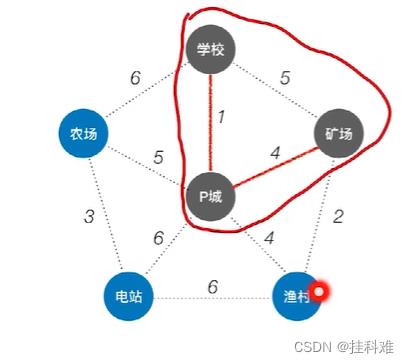
再选择代价最小的顶点并入生成树，依此类推，最小生成树：

Kruskal (克鲁斯卡尔)算法

每次选择一条权值最小的边，使这条边的两头联通(原本已经联通的就不选)，直到所有结点都联通。
还是上面的例子：
首先选出权值最小的一条边，显然是1，使连通。

再选出权值最小的边，<渔村，矿场>权值为2，使连通

再次选择权值最小的边，显然为<农场，电站>3

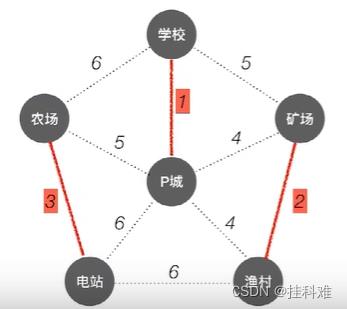
再次重复上述步骤发现，权值最小的边有两个，<P城，矿场>4，<P城，渔村>4，而P城与这两个边均为连通，我们随便选一条，假设选择<P城，矿场>4:

此时P城，矿场，渔村，是连通的，不能再选择<P城，渔村>4这条边了，同理不能选择<学校，矿场>5，而是选择<农场，P城>5边。最小生成树与普雷姆算法一致。

对比

最短路径问题

单源最短路径：即求图中某一顶点到其他各顶点的最短路径。
使用广度优先搜索（BFS）可以实现对无权图的单源最短路径的求解。
但对于有权图来说BFS不在适用，可考虑迪杰斯特拉算法求单源路径长度，求各顶点的最短路径考虑弗洛伊德算法。

Dijkstra(迪杰斯特拉)算法

设有以下图，求V0的单源最短路径：
初始化，发现从V0可以直接到V1, V4。dist[1]表示此刻能找到的从V0到V1的最短路径，V2,V3因为不存在直接和V1相连的边，所以dist为无穷大。path表示路径结点前驱，我们此时最短路径10，5都是由V0直接指向的，所以V1，V4的前驱自然为0（V0）。

第一轮循环：找到还没确定最短路径(即final值为false，dist最小的顶点)，顶点V4，将其设置为true，
为什么要将V4设为true？已经找到了V0到V4的最短路径了吗？是的，因为我们选择的是与V0相邻的，边权值最小的顶点，如果<V0, V4>路径通过V1中转最小，那么第一轮循环选择的顶点应该是V1而不是V4.

检查所有邻接V4的顶点，若其值为false，更新它的dist和path数组信息。如何更新？以V1为例子，检查到V1的路径长度通过V4中转权值会不会更小。V0通过V4中转到V1的路径为8,小于10，修改路径前驱为4。到V2的路径为（5+9）=14 < ∞，修改路径前驱。到V3的距离为5+2=7<∞，修改路径前驱。第一轮处理之后效果如图：

第二轮同理，循环遍历，找到结点V3，与其相连的有V0和V2,V0的final值已经为true了，不用处理，更新V2就可以。

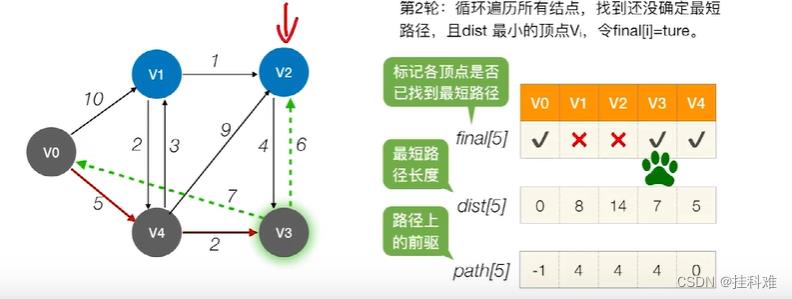
到V3最短路径为7，加上指向V2的边为13 < 14, 更新dist[2]=13, path[2] =3
之后循环同理。处理结束后数组值如图：

求到V2的最短路径：V2的前驱是V1，V1的前驱V4，V4前驱V0，可得到最短路径V0->V4->V1->V2。

时间复杂度

经过n-1轮处理，每次都要遍历所有结点，时间复杂度为O（$n^2$）
迪杰斯特拉算法不适用负权边的情况

Floyd 弗洛伊德算法

初始化一个矩阵，表示各顶点的最短距离，其实就是邻接矩阵名为$A^{-1}$：
刚开始，都不允许中转，path都设置为-1

首先，我们允许通过V0结点进行中转，V2可通过V0到达V1小于之前的无穷，更新数据如下，

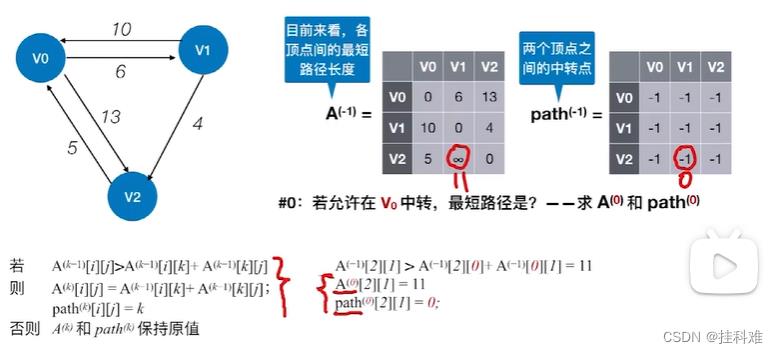
此时得到的矩阵我们称为$A^0$, 在允许通过A1中转，即k=1

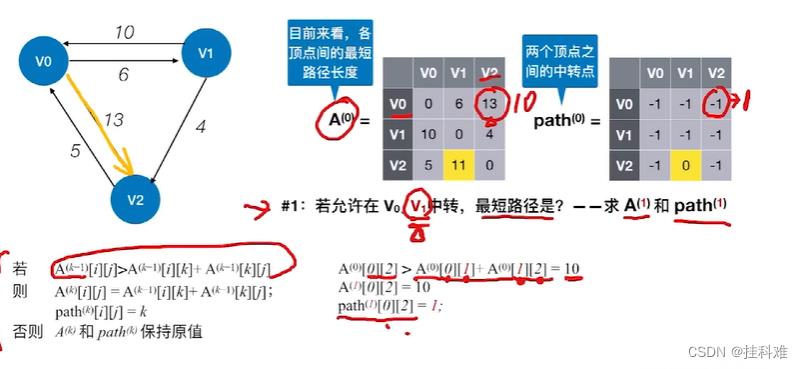
允许V2为中转点，最后矩阵为：

若求V0到V2的路径，0到2的path是1，所以0是先到1，再到V2的。
代码实现

因为n个顶点，每个顶点都要遍历一遍矩阵，时间复杂度为O($n^3$), 空间复杂度为O($n^2$)

总结