读改变未来的九大算法笔记01_数据压缩

Posted 2023-06-02 躺柒

基本思想是发现数据中彼此相同的部分，并运用某种把戏更高效地描述这些部分

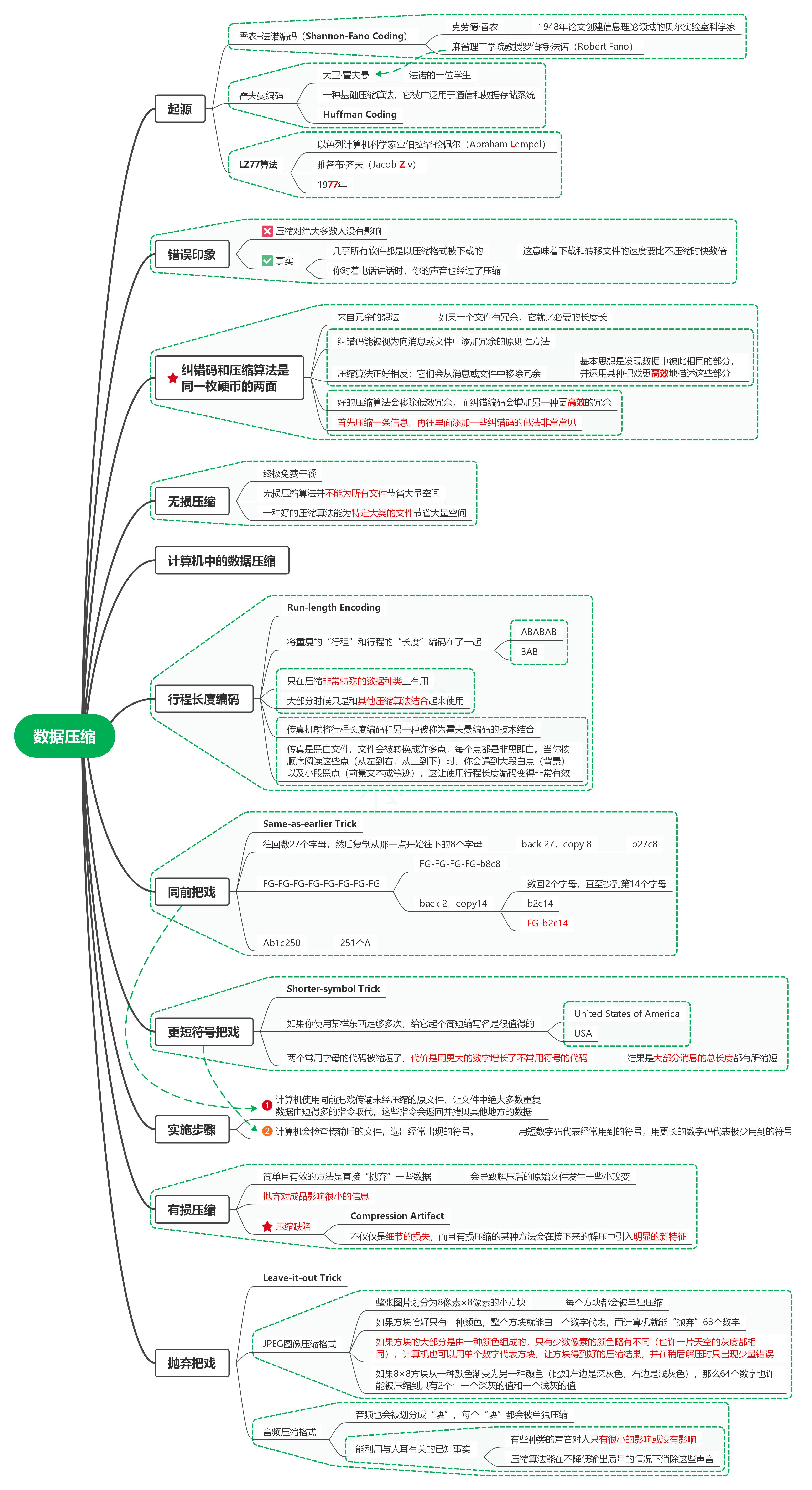
1. 起源

1.1. 香农–法诺编码（Shannon-Fano Coding）

1.1.1. 克劳德·香农

1.1.1.1. 1948年论文创建信息理论领域的贝尔实验室科学家

1.1.2. 麻省理工学院教授罗伯特·法诺（Robert Fano）

1.2. 霍夫曼编码

1.2.1. 大卫·霍夫曼

1.2.1.1. 法诺的一位学生

1.2.2. 一种基础压缩算法，它被广泛用于通信和数据存储系统

1.2.3. Huffman Coding

1.3. LZ77算法

1.3.1. 以色列计算机科学家亚伯拉罕·伦佩尔（Abraham Lempel）

1.3.2. 雅各布·齐夫（Jacob Ziv）

1.3.3. 1977年

2. 错误印象

2.1. 压缩对绝大多数人没有影响

2.2. 事实

2.2.1. 几乎所有软件都是以压缩格式被下载的

2.2.1.1. 这意味着下载和转移文件的速度要比不压缩时快数倍

2.2.2. 你对着电话讲话时，你的声音也经过了压缩

3. 纠错码和压缩算法是同一枚硬币的两面

3.1. 来自冗余的想法

3.1.1. 如果一个文件有冗余，它就比必要的长度长

3.2. 纠错码能被视为向消息或文件中添加冗余的原则性方法

3.3. 压缩算法正好相反：它们会从消息或文件中移除冗余

3.3.1. 基本思想是发现数据中彼此相同的部分，并运用某种把戏更高效地描述这些部分

3.4. 好的压缩算法会移除低效冗余，而纠错编码会增加另一种更高效的冗余

3.5. 首先压缩一条信息，再往里面添加一些纠错码的做法非常常见

4. 无损压缩

4.1. 终极免费午餐

4.2. 无损压缩算法并不能为所有文件节省大量空间

4.3. 一种好的压缩算法能为特定大类的文件节省大量空间

5. 计算机中的数据压缩

6. 行程长度编码

6.1. Run-length Encoding

6.2. 将重复的“行程”和行程的“长度”编码在了一起

6.2.1. ABABAB

6.2.2. 3AB

6.3. 只在压缩非常特殊的数据种类上有用

6.4. 大部分时候只是和其他压缩算法结合起来使用

6.5. 传真机就将行程长度编码和另一种被称为霍夫曼编码的技术结合

6.6. 传真是黑白文件，文件会被转换成许多点，每个点都是非黑即白。当你按顺序阅读这些点（从左到右，从上到下）时，你会遇到大段白点（背景）以及小段黑点（前景文本或笔迹），这让使用行程长度编码变得非常有效

7. 同前把戏

7.1. Same-as-earlier Trick

7.2. 往回数27个字母，然后复制从那一点开始往下的8个字母

7.2.1. back 27，copy 8

7.2.1.1. b27c8

7.3. FG-FG-FG-FG-FG-FG-FG-FG

7.3.1. FG-FG-FG-FG-b8c8

7.3.2. back 2，copy14

7.3.2.1. 数回2个字母，直至抄到第14个字母

7.3.2.2. b2c14

7.3.2.3. FG-b2c14

7.4. Ab1c250

7.4.1. 251个A

8. 更短符号把戏

8.1. Shorter-symbol Trick

8.2. 如果你使用某样东西足够多次，给它起个简短缩写名是很值得的

8.2.1. United States of America

8.2.2. USA

8.3. 两个常用字母的代码被缩短了，代价是用更大的数字增长了不常用符号的代码

8.3.1. 结果是大部分消息的总长度都有所缩短

9. 实施步骤

9.1. 计算机使用同前把戏传输未经压缩的原文件，让文件中绝大多数重复数据由短得多的指令取代，这些指令会返回并拷贝其他地方的数据

9.2. 计算机会检查传输后的文件，选出经常出现的符号。

9.2.1. 用短数字码代表经常用到的符号，用更长的数字码代表极少用到的符号

10. 有损压缩

10.1. 简单且有效的方法是直接“抛弃”一些数据

10.1.1. 会导致解压后的原始文件发生一些小改变

10.2. 抛弃对成品影响很小的信息

10.3. 压缩缺陷

10.3.1. Compression Artifact

10.3.2. 不仅仅是细节的损失，而且有损压缩的某种方法会在接下来的解压中引入明显的新特征

11. 抛弃把戏

11.1. Leave-it-out Trick

11.2. JPEG图像压缩格式

11.2.1. 整张图片划分为8像素×8像素的小方块

11.2.1.1. 每个方块都会被单独压缩

11.2.2. 如果方块恰好只有一种颜色，整个方块就能由一个数字代表，而计算机就能“抛弃”63个数字

11.2.3. 如果方块的大部分是由一种颜色组成的，只有少数像素的颜色略有不同（也许一片天空的灰度都相同），计算机也可以用单个数字代表方块，让方块得到好的压缩结果，并在稍后解压时只出现少量错误

11.2.4. 如果8×8方块从一种颜色渐变为另一种颜色（比如左边是深灰色，右边是浅灰色），那么64个数字也许能被压缩到只有2个：一个深灰的值和一个浅灰的值

11.3. 音频压缩格式

11.3.1. 音频也会被划分成“块”，每个“块”都会被单独压缩

11.3.2. 能利用与人耳有关的已知事实

11.3.2.1. 有些种类的声音对人只有很小的影响或没有影响

11.3.2.2. 压缩算法能在不降低输出质量的情况下消除这些声音

读编程与类型系统笔记05_函数类型

1. 策略模式

1.1. 在运行时从一组算法中选择某个算法

1.1.1. 封装一组算法

1.1.2. 在运行时使用其中一个算法

1.2. 把算法与使用算法的组件解耦

1.3. 面向对象实现

1.3.1. 惯例实现

1.3.2. IStrategy接口

1.3.3. ConcreteStrategy1类

1.3.4. ConcreteStrategy2类

1.3.5. 通过IStrategy接口使用算法的Context类

1.3.6. 常见原因

1.3.6.1. 依赖接口的方法

1.3.6.2. 设计模式在20世纪90年代流行起来

1.3.6.3. 当时并不是所有主流编程语言都支持一等函数

1.4. 函数式实现

1.4.1. Context类

1.4.2. concreteStrategy1()函数

1.4.3. concreteStrategy2()函数

1.4.4. 更简洁的实现

2. 函数的类型

2.1. 函数的签名

2.2. 函数的实参类型和返回类型决定了函数的类型

2.3. 两个函数接受相同的实参，并返回相同的类型

2.3.1. 函数具有相同的类型

3. 一等函数

3.1. 将函数赋值给变量，并像处理类型系统中的其他值一样处理它们

3.2. 一等公民

3.2.1. 赋予它们与其他值相同的权利

3.2.2. 有类型

3.2.3. 可被赋值给变量

3.2.4. 可作为实参传递

3.2.5. 可被检查是否有效

3.2.6. 在兼容的情况下可被转换为其他类型

4. 状态机

4.1. 有一组状态，以及状态之间的转移

4.2. 以给定状态（也叫作开始状态）开始；如果满足特定条件，就能转移到另外一个状态

4.3. 经典的状态机

4.3.1. 将状态集合定义为一个枚举

4.3.2. 跟踪当前的状态

4.3.3. 使用覆盖所有可能状态的switch语句来获得所希望的行为

4.3.4. 使用switch语句的状态机

4.3.4.1. 缺点

4.3.4.1.1. 状态没有与想要在每种状态下运行的逻辑联系在一起

4.3.4.1.2. 状态和转移作为一个单独的枚举进行维护，有不同步的风险

4.4. 使用函数的状态机

4.4.1. 状态完全是由一个函数来表示

4.4.2. 不需要单独跟踪状态

4.4.2.1. 状态与处理逻辑保持同步

4.4.2.2. 去掉了枚举

4.4.2.3. 去掉状态属性

4.4.2.4. 去掉处理转交给合适方法的switch语句

4.4.3. 更简洁的实现

4.4.3.1. 缺点：每种状态关联更多信息要显式声明可能的状态和转移

4.5. 使用和类型的状态机

4.5.1. 把每种状态表示为一个单独的类型

4.5.2. 整个状态机表示为可能状态的一个和类型

4.5.3. 把状态机分解到类型安全的组件中

4.5.4. 比依赖函数的实现更长

4.5.4.1. 优点：允许我们在每种状态中添加属性和成员，把它们组合在一起

4.6. 不使用switch语句的状态机

5. 延迟计算

5.1. 可以传递函数而不是传递实际的值，并在需要值的时候调用这些函数

5.2. 纯粹的面向对象结构可以实现，但是代码比函数式多得多

5.3. 许多函数式编程语言共有的特征

5.3.1. 所有内容都是尽可能晚计算的

5.4. lambda

5.4.1. 匿名函数

5.4.2. 一次性函数

5.4.2.1. 只会引用这种函数一次，所以为其命名就成了多余的工作

6. 立即计算

6.1. 立即得到并传递值，即使我们在以后决定丢弃该值

6.2. 命令式编程语言（如TypeScript、Java、C#和C++）

7. 一阶函数

7.1. 普通函数

7.2. 接受一个或多个非函数实参并返回一个非函数类型的“标准”函数

8. 高阶函数

8.1. 定义：把所有接受或返回其他函数的函数

8.1.1. 二阶函数

8.1.1.1. 接受一个一阶函数作为实参或者返回一个一阶函数的函数

8.1.2. 三阶函数

8.1.2.1. 接受二阶函数作为实参或者返回二阶函数的函数

8.2. 基础算法

8.2.1. map()

8.2.1.1. 给定某个类型的值的一个集合

8.2.1.2. 对其中每个值调用一个函数

8.2.1.3. 返回结果集合

8.2.1.4. 自制map

8.2.1.4.1. 一个T数组和一个函数作为实参

8.2.1.4.2. 该实参函数接受项目T作为实参，并返回U类型的一个值

8.2.1.4.3. 函数把结果添加到一个U数组中

8.2.1.5. C# System.Linq Select()

8.2.1.6. Java java.util.stream map()

8.2.2. filter()

8.2.2.1. 给定一个数据项集合和一个条件

8.2.2.2. 过滤掉不满足该条件的数据项

8.2.2.3. 返回满足该条件的数据项集合

8.2.2.4. 自制filter

8.2.2.4.1. 输入数组的类型为T

8.2.2.4.2. 过滤函数接受T作为实参，并返回boolean结果

8.2.2.4.2.1. 谓词

8.2.2.4.2.1.1. 接受一个实参并返回一个boolean的函数

8.2.2.4.3. 返回过滤后的输出

8.2.2.5. C# System.Linq Where()

8.2.2.6. Java java.util.stream filter()

8.2.3. reduce()

8.2.3.1. 将所有集合项合并为一个值

8.2.3.1.1. 创建一个初始值

8.2.3.1.2. 遍历集合并把每个数据项与累积项合并，不断累积结果

8.2.3.1.3. 遍历完集合后返回累积结果

8.2.3.2. 自制reduce

8.2.3.2.1. 泛型函数

8.2.3.2.1.1. 实参为T数组

8.2.3.2.1.2. 实参T类型的一个初始值

8.2.3.2.1.2.1. 需要处理输入数组为空的情况

8.2.3.2.1.3. 实参一个接受两个T类型的实参并返回T类型的结果

8.2.3.3. C# System.Linq Aggregate()

8.2.3.4. Java java.util.stream reduce()

8.2.3.5. 没有幺半群时

8.2.3.5.1. 考虑初始值是什么

8.2.3.5.2. 在哪个方向上进行缩减

8.3. 抽象代数

8.3.1. 处理集合以及集合上的操作

8.3.2. T值集合上的一个操作

8.3.2.1. 类型T的一个操作接受两个T作为实参，并返回另一个T，即(T, T) => T

8.3.3. 单位元

8.3.3.1. T的一个元素id

8.3.3.2. 操作op(x, id) == op(id, x) == x

8.3.3.3. id与其他任何元素合并起来，并不会改变其他元素

8.3.3.3.1. 操作是加法时，单位元是0

8.3.3.3.2. 操作是乘法时，单位元是1

8.3.3.3.3. 操作为字符串连接时，单位元是“”（空字符串）

8.3.4. 相关性

8.3.4.1. 操作的一个属性

8.3.4.2. 对元素序列应用操作的顺序并不重要，因为最终结果是相同的

8.3.4.3. op(x, op(y, z)) == op(op(x, y), z)

8.3.4.3.1. 加法

8.3.4.3.2. 乘法

8.3.4.3.3. 减法

8.3.4.3.4. 连接两个字符串的首字母

8.3.5. 幺半群（monoid）

8.3.5.1. 有一个单位元

8.3.5.2. 具有相关性

8.3.5.3. 不要求提供初始值

8.3.5.3.1. 在集合为空时默认使用单位元

8.3.6. 半群（semigroup）

8.3.6.1. 没有单位元

8.3.6.1.1. 把初始值放到第一个元素的左边或者最后一个元素的右边很重要

8.3.6.2. 具有相关性