基于arx模型的MPC预测控制器simulink仿真
Posted 51matlab
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了基于arx模型的MPC预测控制器simulink仿真相关的知识，希望对你有一定的参考价值。
1.算法仿真效果
matlab2022a仿真结果如下：
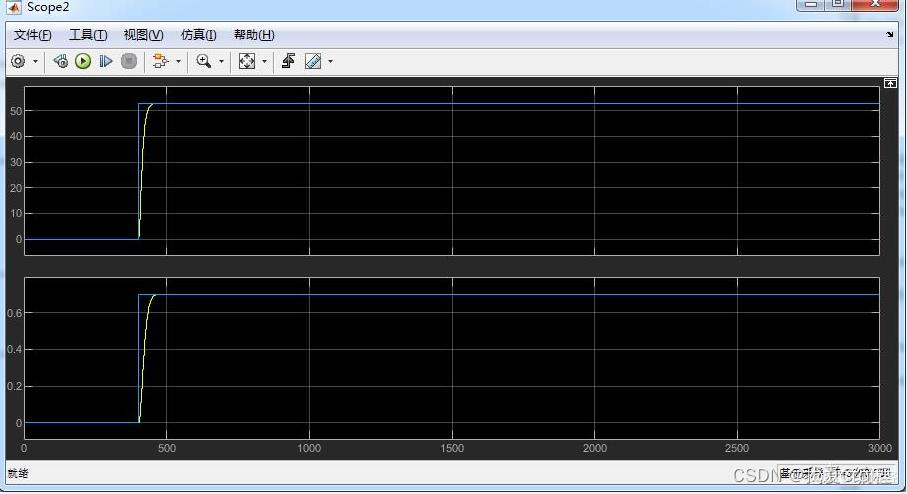
2.算法涉及理论知识概要
arx模型是一种重要的时间序列分析模型，能够用来描述实际应用中的许多问题，在经济、电力系统、车辆驾驶、医疗、信号处理等领域都有着广泛的应用。因此，基于arx模型的相关理论和方法受到了大量关注，这些方法的基本思路常常被归结为:把arx模型看作一个线性回归模型，并利用获得的观测数据实现对该模型参数的准确估计，从而建立准确的arx模型，用来拟合实际的系统。值得注意的是，实际应用中，环境干扰或观测条件等因素可能会导致 arx模型的部分输出观测数据丢失或者观测数据明显异常的情况(以下将这些丢失的输出数据和异常数据统称为丢失数据)。由于arx模型可以等价为一个线性回归模型，因此arx模型部分观测数据的丢失等价于线性回归模型输入矢量信号的丢失，从而导致无法有效实现模型参数的估计。
MPC是一种多变量控制策略，其中涉及了：
过程内环动态模型；控制量的历史数值；在预测区间上的一个最优值方程J。最优控制量可由以上各量求出。
MPC最大的特点在于，相对于LQR控制而言，MPC可以考虑空间状态变量的各种约束，而LQR，PID等控制只能够考虑输入输出变量的各种约束。MPC可应用于线性和非线性系统。
模型预测算法是在欧美等国家兴起的应用于工业领域的一种优化控制算法。目前经过多年的发展，在工业领域、智能控制领域等都有应用。随着算法的理论的完善，其已经成为工业领域内经常使用的一种经典算法。虽然在各个领域算法的应用存在差异。
但他们都遵循预测模型、滚动优化、和反馈校正的基本原理。并且，近年来在汽车工业尤其是在车辆智驾驶技术上，模型预测算法的应用越来越受欢迎。很多科研机构利用了模型预测的原理进行了智能车辆的轨迹跟踪控制研究，下面将详细阐述模型预测算法的原理。
（1）预测模型
预测模型是模型预测控制的基础，它能够通过控制系统中被控平台提供的当前系统状态信息，再加上未来的控制输入变量，预测到未来的被控平台的状态。
预测模型的形式没有确定的形式要求，可以是状态空间方程、传递函数也可以是阶跃响应模型、脉冲响应模型模糊模型等。根据被控对象和需要预测的状态选择合适的预测模型。
对于车辆方向而言，模型预测控制选择状态空间模型比较合适。
（2）滚动优化
预测控制中的优化与通常的离散最优控制算法不同，不是采用一个不变的全局最优目标，而是采用滚动式的有限时域优化策略。
在每一采样时刻，根据该时刻的优化性能指标，求解该时刻起有限时段的最优控制率。计算得到的控制作用序列也只有当前值是实际执行的，在下一个采样时刻又重新求取最优控制率。
也就是说，优化过程不是一次离线完成的，而是反复在线进行（即在每一采样时刻，优化性能指标只涉及从该时刻起到未来有限的时间，而到下一个采样时刻，这一优化时段会同时向前推移）。
通过滚动优化策略，始终在实际的基础上建立新的优化目标，兼顾了对未来有限时域内的理想优化和实际不确定性的影响。这要比建立在理想条件下的传统最优控制更加实际和有效。
（3） 反馈校正
预测控制求解的是一个开环优化问题。在预测控制中，采用预测模型进行过程输出值的预估只是一种理想的方式，对于实际过程，由于存在非线性、时变、模型失配和干扰等不确定因素，使基于模型的预测不可能准确地与实际相符。
因此，在预测控制中，通过输出的测量值与模型的预估值进行比较，得出模型的预测误差，再利用模型预测误差来校正模型的预测值，从而得到更为准确的将来输出的预测值。正是这种由模型加反馈校正的过程，使预测控制具有很强的抗干扰和克服系统不确定的能力。不断根据系统的实际输出对预测输出做出修正，使滚动优化不但基于模型，而且利用反馈信息，构闭环优化控制。
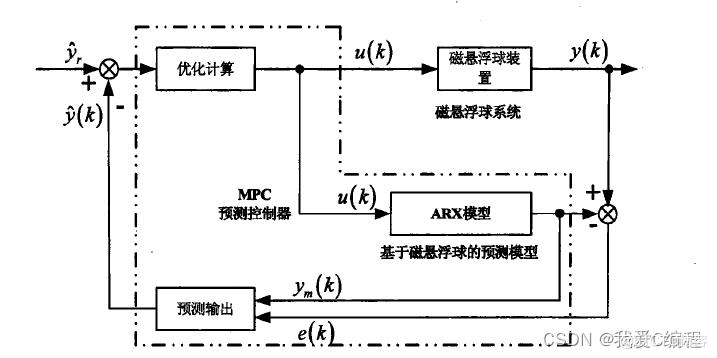
其内部结构框图如下所示：
3.MATLAB核心程序
function [sys,x0,str,ts] = mpc_prediction_controller(t,...
z,...
y,...
flag,...
A_state,...
B_state,...
C_state,...
D_state,...
P,...
M,...
Q,...
R)
%以下是S函数标志流程和格式
persistent MPC_pred Lens
switch flag
case 0
%mpc预测控制器初始化设置
[Rb,Rc] = size(B_state);
Lens = size(C_state,1);
%MPC优化控制器主函数
MPC_pred = mpc_pcontroller(A_state,...
B_state,...
C_state,...
D_state,...
P,...
M,...
Q,...
R);
sizes = simsizes;
sizes.NumContStates = 0;
sizes.NumDiscStates = 0;
sizes.NumOutputs = Rc;
sizes.NumInputs = 2*Lens;
sizes.DirFeedthrough = 1;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
str = [];
x0 = [];
ts = [1 0];
case 2
sys = [];
case 3
din = y(1:Lens);
Ref = y(Lens+1:2*Lens);
sys = MPC_pred(din,Ref);
case 9
sys = [];
otherwise
end
end
基于arx模型的MPC预测控制器simulink建模与仿真实现
目录
一、理论基础
MPC的优点
模型预测控制善于处理多输入多输出系统
对于MIMO系统，PID需要为每个子系统单独设计PID控制器，由于存在耦合对于较大的系统难以实现
1.MPC控制器可以较好控制MIMO系统
2.模型预测控制可以处理约束，安全性约束，上下阈值
3.模型预测控制是有向前考虑未来时间步的有限时域优化（一定的预测能力）最优控制要求在整个时间优化实际上模型预测控制采用了一个折中的策略，既不是像最优控制那样考虑这个时域，也不是完全的贪婪控制仅仅考虑当前，而是考虑未来的有限时间域。
在当今过程控制中，PID当然是用的最多的控制方法，但MPC也超过了10%的占有率。MPC是一个总称，有着各种各样的算法。其动态矩阵控制（DMC）是代表作。DMC采用的是系统的阶跃响应曲线，其突出的特点是解决了约束控制问题。那么是DMC是怎么解决约束的呢？在这里只给出宏观的解释，而不做详细的说明。DMC把线性规划和控制问题结合起来，用线性规划解决输出约束的问题，同时解决了静态最优的问题，一石二鸟，在工业界取得了极大的成功。
2.作用机理
MPC作用机理描述为：在每一个采用时刻，根据获得的当前测量信息，在线求解一个有限时间开环优化问题，并将得到的控制序列的第一个元素作用于被控对象。在下一个采样时刻，重复上述过程：用新的测量值作为此时预测系统未来动态的初始条件，刷新优化问题并重新求解 。
即MPC算法包括三个步骤：
（1）预测系统未来动态；
（2）（数值）求解开环优化问题；
（3）将优化解的第一个元素（或者说第一部分）作用于系统
这三步是在每个采样时刻重复进行的，且无论采用什么样的模型，每个采样时刻得到的测量值都作为当前时刻预测系统未来动态的初始条件
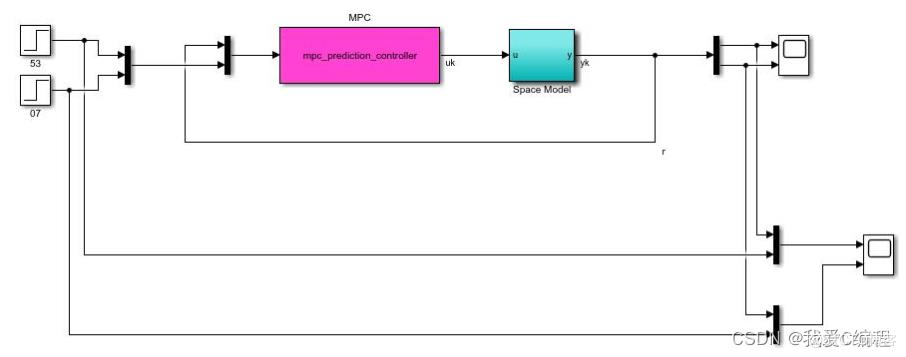
大致的模型建立如下所示：
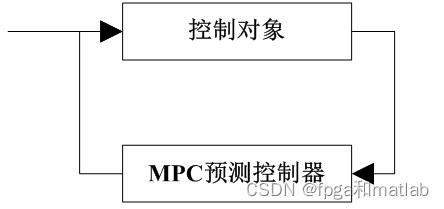
其中MPC预测控制器，采用ARX模型进行设计。其内部结构框图如下所示：
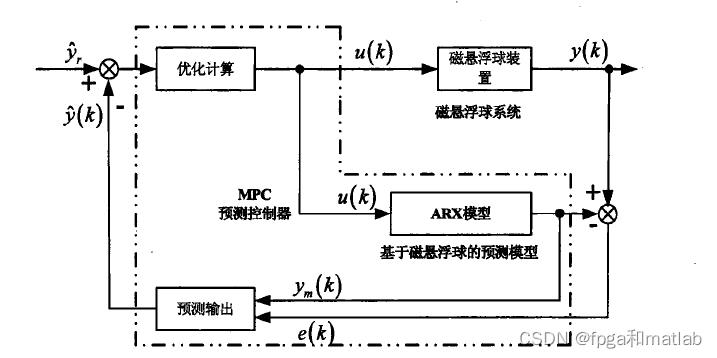
这里虚线部分，就是MPC预测控制器，使用S函数进行设计。
相关公式如下所示：
二、核心程序
下面，就根据上面的结构框图进行系统的simulink建模以及相关S函数的编程实现。
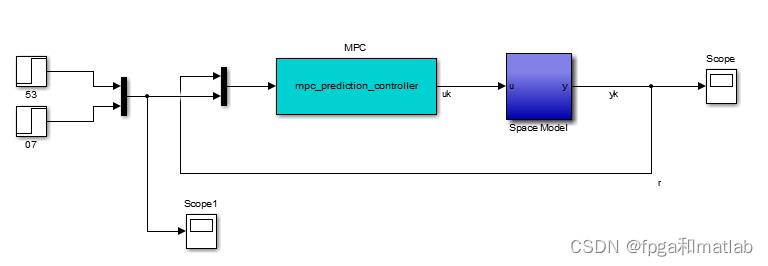
主要是MPC预测控制器的设计，根据论文的结构框图，MPC由三个部分构成，即
优化计算，
ARX模型
预测输出
function Output = mpc_pcontroller(A_state,...
B_state,...
C_state,...
D_state,...
p_cs,...
m_cs,...
Q_cs,...
R_cs)
[Rm,Cn] = size(D_state);
%MPC优化计算
[ak,bk] = Predict_mpc(A_state,...
B_state,...
C_state,...
D_state,...
Cn,...
p_cs,...
m_cs,...
Q_cs,...
R_cs);
x0 = zeros(size(A_state,1),1);
u0 = zeros(Cn,1);
%预测输出
Output = @MPC_pred;
function Output = MPC_pred(din,Ref)
%状态更新
x0 = A_state * x0 + B_state * u0;
if size(Ref,2) < p_cs
ref = [Ref Ref(:,end + zeros(p_cs-size(Ref,2),1))];
else
ref = Ref(:,1:p_cs);
end
%计算误差
Error = abs(din(:) - C_state*x0);
%ARX模型
y1 = -x0;
u1 = reshape(ref-Error(:,ones(p_cs,1)),[],1);
%第一路的输出
ua = sum(ak(1,:) * y1) + sum(bk(1,:) * u1);
%第二路的输出
ub = sum(ak(2,:) * y1) + sum(bk(2,:) * u1);
u0 =[ua;ub];
%控制器输出
Output = u0;
end
end%MPC优化计算
function [Ak,Bk] = Predict_mpc(A_state,...
B_state,...
C_state,...
D_state,...
Ls2,...
p_cs,...
m_cs,...
Q_cs,...
R_cs);
[R1,C1] = size(B_state);
R2 = size(C_state,1);
%根据状态值，获得公式中的G变量
[G1,G2] = func_G_cal(A_state,B_state,C_state,D_state,R1,R2,C1,m_cs,p_cs);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%定义预测矩阵
[P1,P2,P3,L] = func_predict_Matrix(R1,R2,C1,p_cs,A_state,B_state,C_state);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%计算控制系数
[K1,K2] = func_K_cal(G2,P2,P3,L,R2,C1,p_cs,m_cs,Q_cs,R_cs);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%输出a和b系数
Ak = K1(1:Ls2,:);
Bk = K2(1:Ls2,:);
end三、测试结果
仿真结果如下所示：
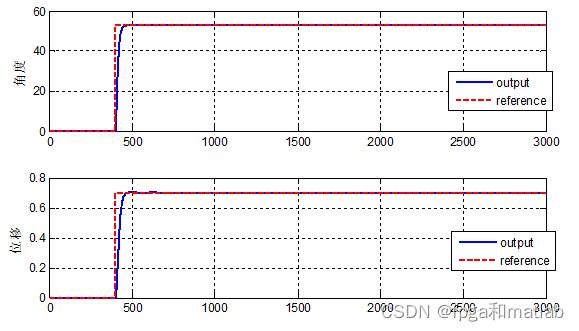
上述的仿真结果，表面本文所研究的MPC预测控制器具有更好的控制性能。
A08-46
以上是关于基于arx模型的MPC预测控制器simulink仿真的主要内容，如果未能解决你的问题，请参考以下文章
Carsim Simulink自动驾驶仿真基于MPC的速度控制
Simulink教程案例5基于Simulink的MPC控制器设计与实现
基于离散连续线性和非线性模型进行模型预测（MPC）控制（Matlab代码实现）