代码随想录算法训练营第17天 | ● 110.平衡二叉树 ● 257. 二叉树的所有路径 ● 404.左叶子之和

Posted 2023-05-30 小懒懒

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了代码随想录算法训练营第17天 | ● 110.平衡二叉树 ● 257. 二叉树的所有路径 ● 404.左叶子之和相关的知识，希望对你有一定的参考价值。

第六章二叉树part04

今日内容：

● 110.平衡二叉树

● 257. 二叉树的所有路径

● 404.左叶子之和

详细布置

迭代法，大家可以直接过，二刷有精力的时候再去掌握迭代法。

110.平衡二叉树（优先掌握递归）

再一次涉及到，什么是高度，什么是深度，可以巩固一下。

题目链接/文章讲解/视频讲解：https://programmercarl.com/0110.%E5%B9%B3%E8%A1%A1%E4%BA%8C%E5%8F%89%E6%A0%91.html

257. 二叉树的所有路径（优先掌握递归）

这是大家第一次接触到回溯的过程，我在视频里重点讲解了本题为什么要有回溯，已经回溯的过程。

如果对回溯似懂非懂，没关系，可以先有个印象。

题目链接/文章讲解/视频讲解：https://programmercarl.com/0257.%E4%BA%8C%E5%8F%89%E6%A0%91%E7%9A%84%E6%89%80%E6%9C%89%E8%B7%AF%E5%BE%84.html

404.左叶子之和（优先掌握递归）

其实本题有点文字游戏，搞清楚什么是左叶子，剩下的就是二叉树的基本操作。

题目链接/文章讲解/视频讲解：https://programmercarl.com/0404.%E5%B7%A6%E5%8F%B6%E5%AD%90%E4%B9%8B%E5%92%8C.html

往日任务

● day 1 任务以及具体安排：训练营一期day 1

● day 2 任务以及具体安排：day 2 第一章数组

● day 3 任务以及具体安排：day 3 第二章链表

● day 4 任务以及具体安排：day 4 第二章链表

● day 5 周日休息

● day 6 任务以及具体安排：day 6 第三章哈希表

● day 7 任务以及具体安排：day 7 第三章哈希表

● day 8 任务以及具体安排：day 8 第四章字符串

● day 9 任务以及具体安排：day 9 第四章字符串

● day 10 任务以及具体安排：day 10 第四章字符串

● day 11 任务以及具体安排：day 11 第五章栈与队列

● day 12 周日休息

● day 13 任务以及具体安排：day 13 第五章栈与队列

● day 14 任务以及具体安排：day 14 第六章二叉树

● day 15 任务以及具体安排：day 15 第六章二叉树

● day 16 任务以及具体安排：day 16 第六章二叉树

代码随想录算法训练营第四十一天| 343. 整数拆分 96.不同的二叉搜索树

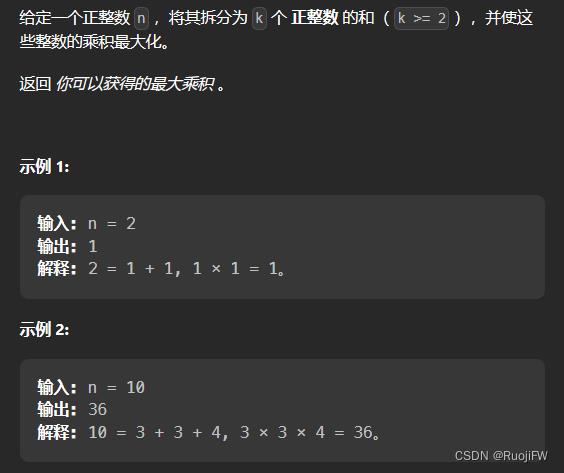
343. 整数拆分

题目链接

思路： 动态规划
动规5步曲：

1、确定dp数组及其下标含义：
dp[i]: 拆分数字 i ，可以得到的最大乘积为dp[i]

2、确定递推公式
从 1 开始遍历 j 然后两种方式得到dp[i]

j * (i - j) 这是拆分为两个数相乘的情况
j * dp[i-j] 这种是拆分成3种以上的情况，想想dp[i]的含义，表示拆分i，
那么这里就可以表示拆分i-j的情况，这里不容易想出来，需要仔细想
所以递推公式是：max(j * (i - j), j * dp[i-j])
然后在取最大值的时候在对比dp[i],拿到真正的最大乘积

3、dp初始化
这里还是比较好想的，因为拆分0和1没有什么意义，那么就从dp[2]开始拆分，
dp[2] = 1 表示拆分2的最大乘积是1

4、确定遍历顺序
dp[i] 是依靠 dp[i - j]的状态，所以遍历i一定是从前向后遍历，先有dp[i - j]再有dp[i]。

因为拆分一个数n 使之乘积最大，那么一定是拆分成m个近似相同的子数相乘才是最大的。
例如 6 拆成 3 * 3， 10 拆成 3 * 3 * 4。 100的话也是拆成m个近似数组的子数相乘才是最大的。
只不过我们不知道m究竟是多少而已，但可以明确的是m一定大于等于2，既然m大于等于2，也就是最差也应该是拆成两个相同的可能是最大值。
那么 j 遍历，只需要遍历到 n/2 就可以，后面就没有必要遍历了，一定不是最大值。

class Solution 
public:
    int integerBreak(int n) 
        //1、确定dp数组以及其下标含义：i拆分的数， dp[i]拆分i的最大乘积
        //2、确定递推公式：固定i，那么拆分就有 i*(i-j)z种情况，拆分(i-j)那么有i*dp[i-j]
        //3。初始化：只有拆分dp[2]有意义，而乘积等于1

        vector<int>dp(n+1);
        dp[2] = 1;

        for (int i = 3; i <= n; i++) 
            for (int j = 1; j <= i / 2; j++) 
                dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
            
        

        return dp[n];
    
;

总结： 这里做了优化，是因为我们每次拆分的时候，这拆分的值值越接近，乘积越大
总体来说做这道题还是不熟练，对于dp我确实是没有什么天赋，只能寄托于以后多刷几遍来增加手感了。

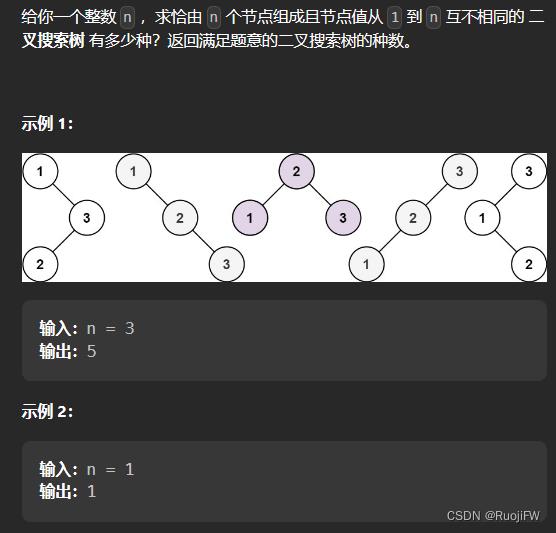
96.不同的二叉搜索树

题目链接

思路：
1、确定dp数组（dp table）以及下标的含义
dp[i] ：到i为节点组成的二叉搜索树的个数为dp[i]。

也可以理解是i个不同元素节点组成的二叉搜索树的个数为dp[i] ，都是一样的。
以下分析如果想不清楚，就来回想一下dp[i]的定义

2、确定递推公式
在上面的分析中，其实已经看出其递推关系， dp[i] += dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量]
j相当于是头结点的元素，从1遍历到i为止。

所以递推公式：dp[i] += dp[j - 1] * dp[i - j]; ，j-1 为j为头结点左子树节点数量，i-j 为以j为头结点右子树节点数量

3、dp数组如何初始化
初始化，只需要初始化dp[0]就可以了，推导的基础，都是dp[0]。

那么dp[0]应该是多少呢？

从定义上来讲，空节点也是一棵二叉树，也是一棵二叉搜索树，这是可以说得通的。

从递归公式上来讲，dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量] 中以j为头结点左子树节点数量为0，也需要dp[以j为头结点左子树节点数量] = 1，否则乘法的结果就都变成0了。

所以初始化dp[0] = 1

4、确定遍历顺序
首先一定是遍历节点数，从递归公式：dp[i] += dp[j - 1] * dp[i - j]可以看出，节点数为i的状态是依靠 i之前节点数的状态。

那么遍历i里面每一个数作为头结点的状态，用j来遍历。

class Solution 
public:
    int numTrees(int n) 
        vector<int>dp(n+1);

        dp[0] = 1;

        for (int i = 1; i <= n; i++) 
            for (int j = 1; j <= i; j++) 
                dp[i] += dp[i-j] * dp[j-1];
            
        
        return dp[n];
    
;