红黑树
Posted 拾荒纪
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了红黑树相关的知识,希望对你有一定的参考价值。
 红黑树的基本操作
红黑树的基本操作
红黑树
杂话
最近闲来无事去学了学红黑树,《算法导论》和维基百科都讲的很详细。
红黑树(英语:Red–black tree)是一种自平衡二叉查找树,是在计算机科学中用到的一种数据结构,典型用途是实现关联数组。它在1972年由鲁道夫·贝尔发明,被称为“对称二叉B树”,它现代的名字源于Leo J. Guibas和罗伯特·塞奇威克于1978年写的一篇论文。红黑树的结构复杂,但它的操作有着良好的最坏情况运行时间,并且在实践中高效:它可以在\\(O(\\log n)\\)时间内完成查找、插入和删除,这里的 \\(n\\) 是树中元素的数目。 ————维基百科
关于红黑树名字的来源也有一个不错的故事(奇怪的名字总会引人遐想:在一篇1972年的论文〈A Dichromatic Framework for Balanced Trees〉中,Leonidas J. Guibas 和 Robert Sedgewick从对称二元B树(symmetric binary B-tree)中推导出了红黑树。之所以选择“红色”是因为这是作者在帕罗奥多研究中心公司(Xerox PARC)工作时用彩色激光打印机可以产生的最好看的颜色。另一种说法来自Guibas,是因为红色和黑色的笔是他们当时可用来绘制树的颜色。故事依旧来自维基百科。
我主要只看了《算法导论》,维基百科只是掠过一眼,所以如果算导和维基上有不一样的我只能按算导来写,不过算导上那个删除操作我看的时候就很惊奇于算导的谜之解释,所以这里按维基上的来,这也是我看算导时想的,不过解释不一样代码都是一样的。
通过本身的性质来维护平衡性,真的tql
性质
红黑树的基本属性有五个:\\(key\\)值,左儿子地址,右儿子地址,父亲地址和它的颜色(红或黑)。
红黑树需要满足以下几点性质:
- 每个点是红色的,或者是黑色的
- 根结点是黑色的
- 每个叶结点(\\(NIL\\))是黑色的
- 如果一个结点是红色的,那么它的两个子结点都是黑色的
- 对于每个结点,其到其所有后代叶结点的简单路径上黑色结点的个数是相等的

为了便于处理边界条件,使用一个哨兵结点来代替所有 \\(NIL\\)

那么,为什么只要维持这几点性质就可以维持树的平衡呢?因为满足红黑性质的树一定是一棵比较平衡的树,对于一个具有 \\(n\\) 个内部结点的树,它的高度至多有 \\(2\\lg(n+1)\\)。算导上有严谨的解释,我在这里简单说一下我的理解:首先我们先不看红色结点,那么黑高是一定的,如果去掉所有红色结点,那么这棵树就是高度平衡的,就算往里添加红色结点,死劲按着一条路径加,根据性质四,这条路径的高度至多变成原来的两倍。因此,平衡树的各种操作在红黑树的执行时间都是 \\(O(\\lg n)\\)。
旋转
和其他平衡树的旋转一样,分为左旋右旋。
 (抠图永无止境……)
(抠图永无止境……)
直接贴代码了:
void left_rotate(int x)
int y = t[x].r;
t[x].r = t[y].l;
if (t[y].l != -1)
t[t[y].l].p = x;
t[y].p = t[x].p;
if (t[x].p == nil) root = y; //特殊设定的nil结点,让nil = maxn - 1;
else if (t[t[x].p].l == x)
t[t[x].p].l = y;
else t[t[x].p].r = y;
t[x].p = y;
t[y].l = x;
void right_rotate(int x)
int y = t[x].l;
t[x].l = t[y].r;
if (t[y].r != -1)
t[t[y].r].p = x;
t[y].p = t[x].p;
if (t[x].p == -1) root = y;
else if (t[t[x].p].l == x)
t[t[x].p].l = y;
else t[t[x].p].r = y;
t[x].p = y;
t[y].r = x;
插入
插入操作与二叉搜索树的插入操作差不多,将插入结点插入到叶结点,然后左右结点设为 \\(nil\\) ,并且将颜色设为红色。操作会破坏红黑性质,所以后来又进行红黑性质的维护。
为什么要设为红色呢?直接设为黑色不久不用违反性质4了吗?但是如果直接设为黑色会影响性质5,在不改变其他结点颜色的情况下性质5是不可能被修复的,窃以为这样较为复杂所以不采用。而且决定红黑树的时间复杂度的关键是黑高,若设定为黑色可能会有多增黑高的可能,这些是个人理解,可能不对。
void insert(int z)
int y = nil, x = root;
while (x != -1)
y = x;
if (t[z].k < t[x].k) x = t[x].l;
else x = t[x].r;
t[z].p = y;
if (y == -1) root = z;
else if (t[z].k < t[y].k)
t[y].l = z;
else t[y].r = z;
t[z].l = -1;
t[z].r = -1;
t[z].c = 0;
insert_fixup(z);
注意到结尾的 \\(insert\\_fixup\\) 函数,这个就是用来修复红黑性质的函数。
void insert_fixup(int z)
while (t[t[z].p].c == 0)
if (t[z].p == t[t[t[z].p].p].l)
int y = t[t[t[z].p].p].r;
if (t[y].c == 0) //case 1
t[t[z].p].c = 1;
t[y].c = 1;
t[t[t[z].p].p].c = 0;
z = t[t[z].p].p;
else if (z == t[t[z].p].r) //case 2
z = t[z].p;
left_rotate(z);
t[t[z].p].c = 1; //case 3
t[t[t[z].p].p].c = 0;
right_rotate(t[t[z].p].p);
else
int y = t[t[t[z].p].p].l;
if (t[y].c == 0)
t[t[z].p].c = 1;
t[y].c = 1;
t[t[t[z].p].p].c = 0;
z = t[t[z].p].p;
else if (z == t[t[z].p].l)
z = t[z].p;
right_rotate(z);
t[t[z].p].c = 1;
t[t[t[z].p].p].c = 0;
left_rotate(t[t[z].p].p);
t[root].c = 1;
共分为6种情况,其中 \\(z\\) 的父结点是左儿子还是右儿子是对称的,把 \\(right\\) 和 \\(left\\) 对换就行,以左儿子为例,分为三种情况:
情况一:插入结点的叔叔存在,且叔叔的颜色是红色。
为了避免出现连续的红色结点,我们可以将父结点和叔结点变黑,将祖父结点变红。这样一来既保持了每条路径黑色结点的数目不变,也解决了连续红色结点的问题。
但是这样就出现一个新的问题:祖父结点就可能不满足红黑性质了,于是我们将祖父结点设为新的 \\(z\\) 继续修改。
还有一个问题是:如果 \\(g\\) 正好是根结点了怎么办?所以在每次循环的末尾都要将根结点设为黑色,只有这个时候红黑树的黑高才会增加。
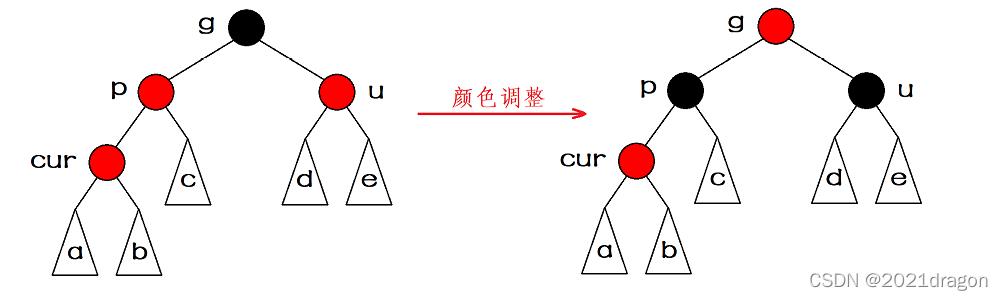
情况二:插入结点的叔结点存在,且叔结点的颜色是黑色,并且 \\(z\\) 是一个右孩子。
我们直接左旋一下,使它变成情况三

情况三:插入结点的叔结点存在,且叔结点的颜色是黑色,并且 \\(z\\) 是一个左孩子。
出现叔叔存在且为黑时,单纯使用变色已经无法处理了,这时我们需要进行旋转处理。祖孙三代的关系是直线(x、父亲、祖父这三个结点为一条直线),正是情况三,则我们需要先进行单旋操作,再进行颜色调整,颜色调整后这棵被旋转子树的根结点是黑色的,因此无需继续往上进行处理。
因为只有一条直线才能旋起来,所以情况二就先处理成情况三。
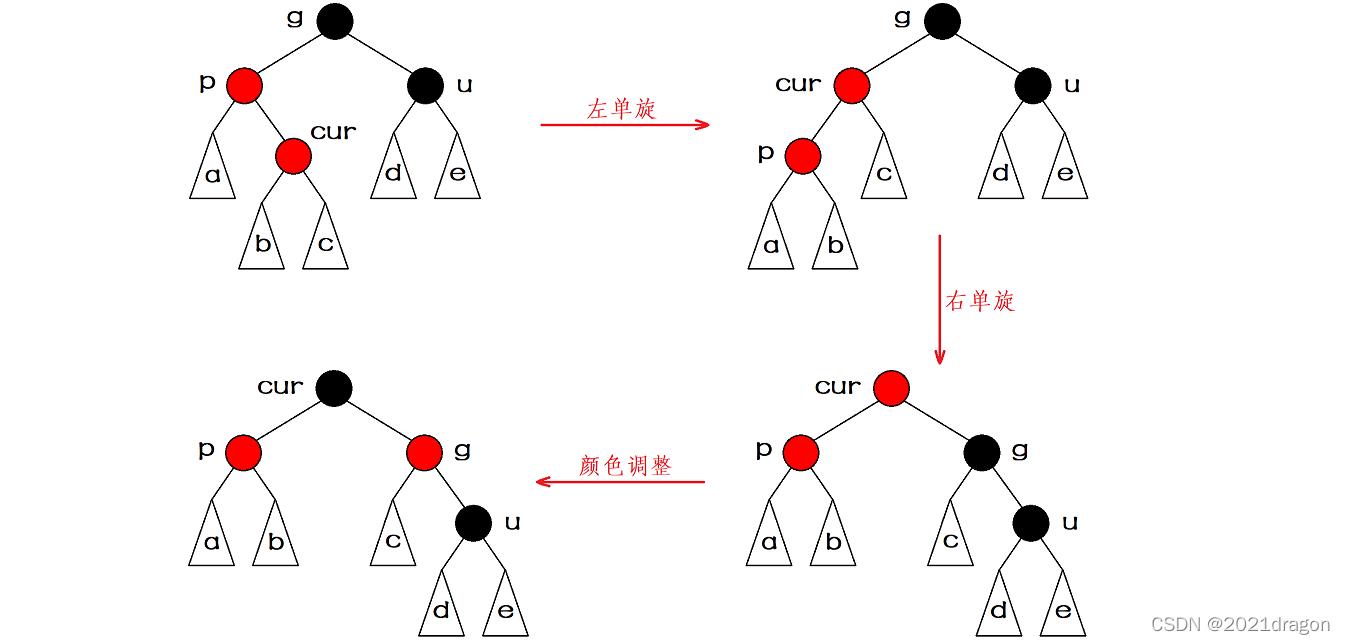
有的博客将叔结点不存在还算成了一种情况,其实是多余的,因为叔结点不存在既是 \\(nil\\) ,而 \\(nil\\) 的颜色是黑的,等同于情况二和情况三。
对于 \\(fixup\\) 操作维持红黑树性质的严谨证明,算法导论上说的很详细,但奈何我非常懒不想再抄一遍并且找不到电子书来截图……
时间复杂度是 \\(log\\)
并且我们注意到插入实际上是原地算法,因为上述所有调用都使用了尾部递归。
删除
RB-delete删除 = 二叉树的删除+删除修复(delete_fixup)
做二叉树删除时,需要记录被调整节点的颜色。
二叉搜索树删除的四种情况

void rb_delete(int z)
int y = z;
bool delcol = t[y].c;
int x = z;
if (t[z].l == nil)
x = t[z].r;
rb_transplant(z, t[z].r);
else if (t[z].r == nil)
x = t[z].l;
rb_transplant(z, t[z].l);
else
y = find_min(t[z].r);
delcol = t[y].c;
x = t[y].r;
if (t[y].p == z)
t[x].p = y;
else
rb_transplant(y, t[y].r);
t[y].r = t[z].r;
t[t[y].r].p = y;
rb_transplant(z, y);
t[y].l = t[z].l;
t[t[y].l].p = y;
t[y].c = t[z].c;
if (delcol == 1)
rb_delete_fixup(x);
为什么要记录被调换的那个 \\(y\\) 结点的颜色呢?而且我们注意到只有被调整结点颜色为黑色时才会进行调整操作,这是因为删除节点之前性质5是满足的,但是如果在一条路径上去掉一个结点,并且这个结点是黑色的,那么性质5显然就不满足了,所以要进行调整。算法导论上将修改操作解释为“认为改变后的结点有双重颜色,破坏了性质1,故进行修复操作来恢复性质1、性质2、性质4”,窃以为多此一举,不如按维基百科上破坏性质5解释来的自然。
先给出 \\(fixup\\) 代码:
void rb_delete_fixup(int x)
while (x != root && t[x].c == 1)
if (x == t[t[x].p].l)
int w = t[t[x].p].r;
if (t[w].c == 0) //A: CASE 1
t[w].c = 1;
t[t[x].p].c = 0;
left_rotate(t[x].p);
w = t[t[x].p].r;
if (t[t[w].l].c == 1 && t[t[w].r].c == 1) //A: CASE 2
t[w].c = 0;
x = t[x].p;
else
if (t[t[w].r].c == 1) //A: CASE 3
t[t[w].l].c = 1;
t[w].c = 0;
right_rotate(w);
w = t[t[x].p].r;
t[w].c = t[t[x].p].c; //A: CASE 4
t[t[x].p].c = 1;
t[t[w].r].c = 1;
left_rotate(t[x].p);
x = root;
else
int w = t[t[x].p].l;
if (t[w].c == 0) //B: CASE 1
t[w].c = 1;
t[t[x].p].c = 0;
right_rotate(t[x].p);
w = t[t[x].p].l;
if (t[t[w].r].c == 1 && t[t[w].l].c == 0) //B: CASE 2
t[w].c = 0;
x = t[x].p;
else
if (t[t[w].l].c == 1) //B: CASE 3
t[t[w].r].c = 1;
t[w].c = 0;
left_rotate(w);
w = t[t[x].p].l;
t[w].c = t[t[x].p].c; //B: CASE 4
t[t[x].p].c = 1;
t[t[w].l].c = 1;
right_rotate(t[x].p);
x = root;
t[x].c = 1;
分为4种情况:
情况一:\\(X\\) 的兄弟结点 \\(w\\) 是红色的
当待删除结点的兄弟为红色时,我们先以父亲为旋转点进行一次左单旋,再将兄弟的颜色变为黑色,将父亲的颜色变为红色,此时我们再对结点 \\(x\\) 进行情况分析,情况一就转换成了情况二、三或四。

当结点 \\(w\\) 为黑色时,属于情况2、3、4,这些情况是由 \\(w\\) 的颜色来区分的。
情况二:\\(x\\) 的兄弟结点是黑色的,且 \\(w\\) 的两个子结点是黑色的
因为在删除时将 \\(B-X\\) 这一路的结点提上去一个,所以这一路的黑色结点显然少一个。
在该情况下,我们直接将兄弟的颜色变成红色,此时根据父亲的颜色决定红黑树的调整是否结束,若父亲的颜色是红色,则我们将父亲变为黑色后即可结束红黑树的调整;若父亲的颜色原本就是黑色,则我们需要将父亲结点当作下一次调整时的 \\(x\\) 结点进行情况分析,并且情况二在下一次调整时可能会是情况一、二、三、四当中的任何一种。

情况三: \\(x\\) 的兄弟结点是黑色的,且 \\(w\\) 的左儿子是红色,右儿子是黑色
出现该情况时,我们先以兄弟为旋转点进行一次右单旋,再将兄弟结点变为红色,将兄弟结点的左儿子变为黑色,此时我们再对 \\(x\\) 进行情况分析,情况三就转换成了情况四。

情况四:\\(x\\) 的兄弟结点是黑色的,且 \\(w\\) 的左儿子是黑色的,右儿子是红色的
经过情况四的处理后,红黑树就一定调整结束了。在情况四当中,我们先以父亲为旋转点进行一次左单旋,然后将父亲的颜色赋值给兄弟,再将父亲的颜色变为黑色,最后将 \\(w\\) 的右儿子变为黑色,此时红黑树的调整便结束了。

后记
真的是写前踌躇满志,写时痛苦面具,写后怅然若失。自己对于红黑树依旧是没有怎么掌握,只能不断地翻书查资料,书上写的有些过于严谨导致读来不畅,网上的博客大部分也只是介绍了一下操作,然而原理还是有些地方不懂,而有一些博客看上去似乎非常好但是太长了我也不敢看。
现在仍然有一些缺陷:
-
首先是代码,网上的都是用指针实现的,但是我对于指针实在是不太熟练,而且听说有一些地方用指针反而会慢一些,所以用的是数组,但是我太烂了,写了几个基本操作就放弃了,想要测试一下代码对不对总不能手推树的结构然后输出检验吧,那样太繁琐了,我竟没有知道这代码对不对了
-
然后则是一些原理仍不是很明白,反应在这篇博客中也是语焉不详,譬如,fixup操作,为什么要那样做?尤其是delete_fixup的解释,是解释成破坏性质1还是性质5?算导的固然不自然,在解释时似乎能自圆其说,但推敲一番觉得情况二“同时去掉一重黑色”的解释很怪异,似乎在说底色是红色,然后x染了两重黑,w是一层,但是去掉后w岂不就无色了?底色可以看作红黑色,那我两重黑色就不是红黑色了?然而如果用性质5我却无法证明。
-
还有一点是对于那些操作的描述,由于都是相同的,我自己懒得写,于是只能搬一下了,还有图也是,这导致这篇文章像一个缝合怪,有的地方颇不自然
红黑树介绍与实现
尽力做好一件事,实乃人生之首务。
红黑树的概念
红黑树是指每个节点都带有颜色属性的二叉搜索树,其颜色不是红色就是黑色,并且要在二叉搜索树的基础上要满足一些特殊的性质,因此被我们称之为红黑树。
红黑树的性质
一棵红黑树是满足下面红黑性质的二叉搜索树:
- 每个结点不是红色就是黑色。
- 根结点是黑色的。
- 如果一个结点是红色的,则它的两个子结点都是黑色的 (即不能出现连续的红结点)。
- 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点。
- 每个叶节点(NIL)是黑色的 (此处的叶子结点指的是空结点)。
推论:
最短路径:全部都是由黑色结点构成。
最长路径:一黑一红,红色结点的数量和黑色结点的数量相同。
注意:正常红黑树中,不一定有全黑的最短路径和一黑一红的最长路径。
红黑树结点的定义
这里我们使用枚举类型来定义红黑树的颜色,当然也可以利用如bool类型来表示都是可以的。其中这里我们将结点定义成K-V模型,这是为了后面的博客中我们要用这同一颗红黑树来模拟实现map与set容器。
代码如下:
//节点的颜色
enum class Color
RED,
BLACK
;
//K-V模型
template<class K,class V>
struct RBTreeNode //三叉链
RBTreeNode<K,V>* m_left; //左节点
RBTreeNode<K,V>* m_right; //右节点
RBTreeNode<K,V>* m_parent; //节点的父结点(红黑树需要 旋转 ,为了实现简单给出的该字段)
pair<K, V>m_kv; //节点数据
Color m_col; //节点颜色
RBTreeNode(const pair<K, V>& kv)
: m_left(nullptr), m_right(nullptr), m_parent(nullptr)
, m_kv(kv),m_col(Color::RED)
;
红黑树的插入操作
在我们要进行插入操作时,我们要想一个问题我们是插入黑色结点好,还是插入红色结点好呢?下面我们进行分析:
- 新插入的结点是红色,可能会破坏性质3,这导致有连续的红色结点,但也只影响这一条路径,影响不大。
- 新插入的结点是黑色,一定会破坏性质4,这导致每条路径的黑色结点数目不相同,破坏性强!!!
综上所述,我们选择新插入结点时插入红色结点。
红黑树是在二叉搜索树的基础上加上一些特殊的平衡限制性质,因此红黑树的插入与二叉搜索树插入类似,具体红黑树插入可分为两步:
- 先按照二叉搜索树的规则先找到插入位置,并插入。
- 再检测这个新插入的结点插入后,红黑树的性质是否遭到破坏。
由于新结点插入的颜色默认是红色,因此如果双亲parent为黑色,则不需要调整,直接插入完成,退出插入操作。
但如果双亲parent为红色时,这样就违反了性质3不能存在连续的红色结点的情况,因此需要对红黑树来进行调整,具体情况如下所示
- 情况一:cur为红(新增结点),parent为红,grandfather为黑,uncle存在且为红。
处理方案为:parent和uncle变为黑色,grandfather变为红,但调整还没有结束,因为此时祖父结点变成了红色,我们要再判断祖父的父结点是否为红色,若其父结点也是红色,那么又需要根据其叔叔的不同,进而进行不同的调整操作。然后继续向上处理,直到parent存在且为黑的时候停止,或者parent不存在停止,如果grandfather是根,那么将根变黑。


- 情况二:cur为红(新增结点),parent为红,且cur与parent为直线的时候,uncle不存在或者存在且为黑。
处理方案为:旋转加变色处理,grandfather变红,parent变黑。
并且uncle存在,一定是黑色,那么cur结点原来的颜色一定也是黑色的,现在看到是红色的原因是因为cur的子树再颜色调整的过程中将cur结点的颜色由黑色改变成红色,即从情况1向上处理后碰到情况2的情况,具体如下图中的例2所示:
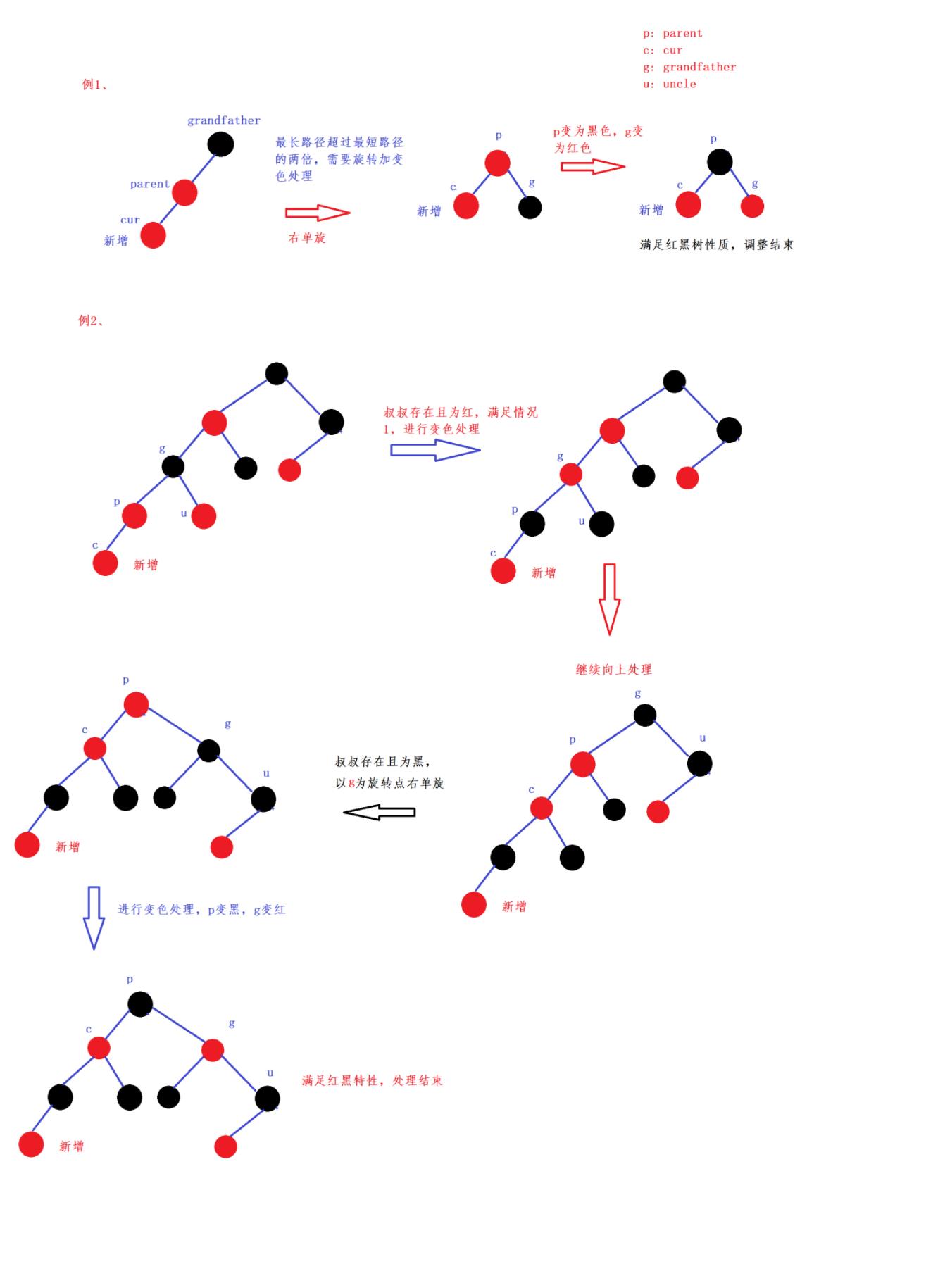
- 情况三:cur为红(新增结点),parent为红,且cur与parent为折线的时候,uncle不存在或者存在且为黑。
处理方案为:双旋加变色处理,cur变黑,grandfather变红。
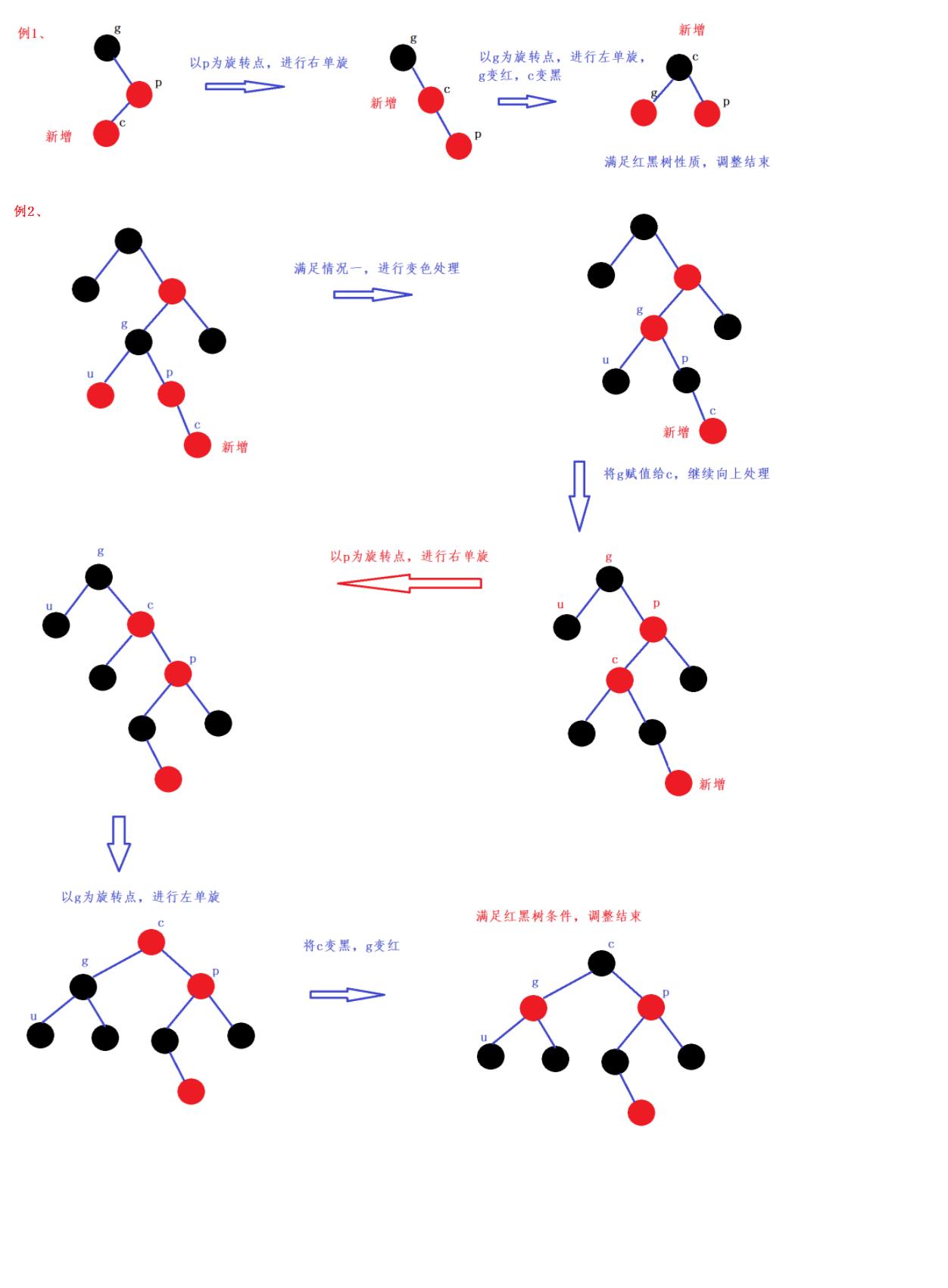
代码如下:
//传进来的是不平衡的结点的指针
void RotateL(Node* parent) //左旋
Node* subR = parent->m_right; //出问题的右结点
Node* subRL = subR->m_left; //出问题的右结点的左结点
parent->m_right = subRL; //首先先将我们的parent的右指向subRL
if (subRL != nullptr) //再将subRL的父亲指向parent结点,但这样要判断一下是否是空指针,如果subRL是空指针的话,
//那么解引用它会出现问题
subRL->m_parent = parent;
Node* curParent = parent->m_parent; //拿一个结点存储parent的父亲
parent->m_parent = subR; //再使得parent的父亲指针指向它原先的右结点(subR)
subR->m_left = parent; //在让subR的左指向parent
if (parent == m_root) //在这里得判断一下它是否为根,如果parent为根的话,那么我们的根结点指针也得改变
//并且将subR的父亲指针置为空,此时subR此时为根结点
m_root = subR;
subR->m_parent = nullptr;
else
//如果不为头节点,那么我们只需要将subR的父亲指针指向parent之前的父亲结点
if (curParent->m_left == parent)
curParent->m_left = subR;
else
curParent->m_right = subR;
subR->m_parent = curParent;
void RotateR(Node* parent) //右旋
Node* subL = parent->m_left;
Node* subLR = subL->m_right;
parent->m_left = subLR;
if (subLR != nullptr)
subLR->m_parent = parent;
Node* curParent = parent->m_parent;
parent->m_parent = subL;
subL->m_right = parent;
if (parent == m_root)
m_root = subL;
subL->m_parent = nullptr;
else
if (curParent->m_left == parent)
curParent->m_left = subL;
else
curParent->m_right = subL;
subL->m_parent = curParent;
//插入看叔叔
std::pair<Node*, bool> insert(const std::pair<K, V>& kv)
if (m_root == nullptr) //如果红黑树为空树,直接插入结点并将该结点作为根结点即可
m_root = new Node(kv);
m_root->m_col = Color::BLACK;
return std::make_pair(m_root, true);
//按照二叉搜索树的插入方法,找到要插入的位置
Node* parent = nullptr;
Node* cur = m_root;
while (cur != nullptr)
if (cur->m_kv.first > kv.first)
parent = cur;
cur = cur->m_left;
else if (cur->m_kv.second < kv.first)
parent = cur;
cur = cur->m_right;
else
return std::make_pair(cur, false);
//判断新增结点这个位置是在该位置parent的左边还是右边
//并将其链接起来
Node* newNode = new Node(kv);
if (parent->m_kv.first > kv.first)
parent->m_left = newNode;
newNode->m_parent = parent;
else
parent->m_right = newNode;
newNode->m_parent = parent;
cur = newNode;
//3、调颜色,如果插入的结点的父亲是红色得到我们就需要进行调整
while (parent != nullptr && parent->m_col == Color::RED)
Node* grandFather = parent->m_parent;
if (parent == grandFather->m_left) //情况一:叔叔存在且为红
Node* uncle = grandFather->m_right;
if (uncle != nullptr && uncle->m_col == Color::RED)
uncle->m_col = parent->m_col = Color::BLACK;
grandFather->m_col = Color::RED;
cur = grandFather;
parent = cur->m_parent;
else
if (cur == parent->m_left) //情况二:叔叔存在且为黑直线或者不存
RotateR(grandFather);
grandFather->m_col = Color::RED;
parent->m_col = Color::BLACK;
else //情况三:叔叔存在且为黑折线或者不存
RotateL(parent);
RotateR(grandFather);
cur->m_col = Color::BLACK;
grandFather->m_col = Color::RED;
break;
else
Node* uncle = grandFather->m_left;
if (uncle != nullptr && uncle->m_col == Color::RED)
uncle->m_col = parent->m_col = Color::BLACK;
grandFather->m_col = Color::RED;
cur = grandFather;
parent = cur->m_parent;
else
if (cur == parent->m_left)
RotateR(parent);
RotateL(grandFather);
grandFather->m_col = Color::RED;
cur->m_col = Color::BLACK;
else
RotateL(grandFather);
grandFather->m_col = Color::RED;
parent->m_col = Color::BLACK;
break;
m_root->m_col = Color::BLACK; //始终让根结点为黑色
return std::make_pair(newNode, true);
在插入中的旋转方式,在这里就不在叙述了,看不懂的话可以看我的AVL树的博客在哪里有具体的讲解。
红黑树的验证
由于我们直到红黑树是一种满足某种特殊性质的二叉搜索树,因此我们可以先获取到二叉树的中序序列,来判断该二叉树是否满足二叉搜索树的性质。
其中中序遍历的代码如下:
private:
void _Inorder(Node*& root)
if (root == nullptr)
return;
_Inorder(root->m_left);
cout << root->m_kv.first << " : " << root->m_kv.second << endl;
_Inorder(root->m_right);
public:
void Inorder()
_Inorder(m_root);
cout << endl;
在这里我们利用两个函数来进行书写,这样做的好处是,外层用户不会直接去使用到根结点,它只需要看到结果即可。但中序遍历出来有序,只能保证它是一棵二叉搜索树,并不能保证它是满足红黑树树的性质。
故我们还要验证是否满足红黑树的五条性质,原理是先从根开始计算最左路黑色结点个数,那么只需要从根开始遍历只要每条路径到空位置,黑色结点个数相同即可直到是否满足每条路径都有相同数量的黑色结点。
代码如下:
public:
//判断是否为红黑树
bool IsRBTree()
if (m_root == nullptr) //空树是红黑树
return true;
if (m_root->m_col == Color::RED)
cout << "error:根结点为红色" << endl;
return false;
//找最左路径作为黑色结点数目的参考值
Node* cur = m_root;
int BlackCount = 0;
while (cur)
if (cur->m_col == Color::BLACK)
BlackCount++;
cur = cur->m_left;
int count = 0;
return _IsRBTree(m_root, count, BlackCount);
private:
//判断是否为红黑树的子函数
bool _IsRBTree(Node* root, int count, int BlackCount)
if (root == nullptr) //该路径已经走完了
if (count != BlackCount)
cout << "error:黑色结点的数目不相等" << endl;
return false;
return true;
if (root->m_col == Color::RED && root->m_parent->m_col == Color::RED)
cout << "error:存在连续的红色结点" << endl;
return false;
if (root->m_col == Color::BLACK)
count++;
return _IsRBTree(root->m_left, count, BlackCount) && _IsRBTree(root->m_right, count, BlackCount);
故红黑树的验证分为以下两步:
- 通过中序遍历来判断是否是二叉搜索树,因为首先要满足是搜索树这是红黑树的前提。
- 在搜索树的前提下,再通过验证是否满足红黑树的性质来判断是否是红黑树。
红黑树的删除
红黑树的删除大致和AVL树的删除差不多,只是在AVL树删除是要调节平衡因子,而红黑树删除是要调节使其满足红黑树的五条性质。
与AVL树删除同样。
- 首先都是先找到要删除的结点,并用替代法将结点删除。因此我们最终需要删除的都是左右子树至少有一个为空的结点。找到实际待删除结点后,先不直接删除该结点,我们先调整红黑树让其删除后任然满足红黑性质,所以我们找到实际待删除结点之后立即对红黑树进行调整。
- 其次就是调整红黑树,使其删除该结点之后仍然满足红黑树的性质。最后就是删除,并把链接关系建立好即可。
我们先从最简单的出发,如果要删除的节点是 a,它只有一个子节点 b,那我们就依次进行下面的操作。
处理方式为:删除节点 b,并且把节点 b的数据替换到节点 a 的位置。并且这个节点 a 只能是黑色,节点 b 也只能是红色,其他情况均不符合红黑树的性质。这种调整结束后不需要进行二次调整,直接退出即可。

这里需要注意一下,红黑树的定义中“只包含红色节点和黑色节点”,经过初步调整之后,为了保证满足红黑树定义的最后一条要求,有些节点会被标记成两种颜色,“红 - 黑”或者“黑 - 黑”。如果一个节点被标记为了“黑 - 黑”,那在计算黑色节点个数的时候,要算成两个黑色节点。
在下面的讲解中,如果一个节点既可以是红色,也可以是黑色,在画图的时候,我会用一半红色一半黑色来表示。如果一个节点是“红 - 黑”或者“黑 -黑”,我会用左上角的一个小黑点来表示额外的黑色。 其中x、y、z、w、p、q等都是表示子树,可以只为NIL结点。
CASE 1:如果关注节点是 a,它的兄弟节点 c 是红色的,我们就依次进行下面的操作:
- 围绕关注节点 a 的父节点 b 左旋;
- 关注节点 a 的父节点 b 和祖父节点 c 交换颜色,关注节点不变,更新兄弟结点,此时兄弟结点就变为了d;
这样就从CASE 1 转变为 后面的CASE 2、3、4这三种情况继续进行调整。

CASE 2 : 如果关注节点是 a,它的兄弟节点 c 是黑色的,并且节点 c 的左右子节点 d、e 都是黑色的,我们就依次进行下面的操作:
- 将关注节点 a 的兄弟节点 c 的颜色变成红色;
- 从关注节点 a 中去掉一个黑色,这个时候节点 a 就是单纯的红色或者黑色;
- 给关注节点 a 的父节点 b 添加一个黑色,这个时候节点 b 就变成了“红 - 黑”或者“黑 - 黑”;
3.1 此时结点b变为了“红 - 黑”,即b的颜色原来是单纯的红色时,我们将b的颜色变成黑色后结束调整;
3.2 此时结点b变为了“黑 - 黑”,即b的颜色原来是单纯的黑色时,我们继续向上更新,最后我们将关注节点从 a 变成其父节点 b;
这样我们就继续从四种情况中选择符合的规则来进行调整。

CASE 3:如果关注节点是 a,它的兄弟节点 c 是黑色,c 的左孩子节点 d 是红色,c 的右孩子节点 e 是黑色,我们就依次进行下面的操作:
- 首先我们围绕关注节点 a 的兄弟节点 c 右旋;
- 其次是节点 c 和节点 d 交换颜色;关注节点不变,但要和CASE 1 一样要更新关注结点的兄弟结点;
从CASE 3 一定会跳转到 CASE 4,继续调整。
CASE 4:如果关注节点 a 的兄弟节点 c 是黑色的,并且 c 的右子节点是红色的,我们就依次进行下面的操作:
- 首先我们围绕关注节点 a 的父节点 b 进行左旋;
- 将关注节点 a 的兄弟节点 c 的颜色,跟关注节点 a 的父节点 b 设置成相同的颜色;然后将关注节点 a 的父节点 b 的颜色设置为黑色;从关注节点 a 中去掉一个黑色,节点 a 就变成了单纯的红色或者黑色;将关注节点 a 的叔叔节点 e 设置为黑色;
CASE 4 调整完后就结束调整。

CASE 1 、3 和4在各自执行常数次数的颜色改变和至多3次旋转后便终止。而CASE 2 是 while 循环可以重复执行的唯一情况,然后指针x沿树上升至多O(logn)次,且不执行任何旋转。
- 最后就是进行结点的删除。删除该结点判断删除结点是否有孩子,将删除结点的孩子结点的m_parent链接到删除结点的父亲,然后再将删除结点的父亲的m_left或者m_right链接到孩子。
代码如下:
public:
//删除函数 删除看兄弟
bool erase(const K& key)
//用于遍历二叉树
Node* parent = nullptr;
Node* cur = m_root;
//用于标记实际的待删除结点及其父结点
Node* delParentPos = nullptr;
Node* delPos = nullptr;
while (cur != nullptr)
if (key < cur->m_kv.first) //所给key值小于当前结点的key值
//往该结点的左子树走
parent = cur;
cur = cur->m_left;
else if (key > cur->m_kv.first) //所给key值大于当前结点的key值
//往该结点的右子树走
parent = cur;
cur = cur->m_right;
else //找到了待删除结点
if (cur->m_left == nullptr) //待删除结点的左子树为空
if (cur == m_root) //待删除结点是根结点
m_root = m_root->m_right; //让根结点的右子树作为新的根结点
if (m_root)
m_root->m_parent = nullptr;
m_root->m_col = Color::BLACK; //根结点为黑色
delete cur; //删除原根结点
return true;
else
delParentPos = parent; //标记实际删除结点的父结点
delPos = cur; //标记实际删除的结点
break; //进行红黑树的调整以及结点的实际删除
else if (cur->m_right == nullptr) //待删除结点的右子树为空
if (cur == m_root) //待删除结点是根结点
m_root = m_root->m_left; //让根结点的左子树作为新的根结点
if (m_root)
m_root->m_parent = nullptr;
m_root->m_col = Color::BLACK; //根结点为黑色
delete cur; //删除原根结点
return true;
else
delParentPos = parent; //标记实际删除结点的父结点
delPos = cur; //标记实际删除的结点
break; //进行红黑树的调整以及结点的实际删除
else //待删除结点的左右子树均不为空
//替换法删除
//寻找待删除结点右子树当中key值最小的结点作为实际删除结点
Node* minParent = cur;
Node* minRight = cur->m_right;
while (minRight->m_left != nullptr)
minParent = minRight;
minRight = minRight->m_left;
cur->m_kv.first = minRight->m_kv.first; //将待删除结点的key改为minRight的key
cur->m_kv.second = minRight->m_kv.second; //将待删除结点的value改为minRight的value
delParentPos = minParent; //标记实际删除结点的父结点
delPos = minRight; //标记实际删除的结点
break; //进行红黑树的调整以及结点的实际删除
if (delPos == nullptr) //delPos没有被修改过,说明没有找到待删除结点
return false;
//记录待删除结点及其父结点(用于后续实际删除)
Node* del = delPos;
Node* delP = delParentPos;
//调整红黑树 为了删除黑色结点后来恢复红黑树的性质
if (delPos->m_col == Color::BLACK) //删除的是黑色结点
if (delPos->m_left != nullptr) //待删除结点有一个红色的左孩子(不可能是黑色)
delPos->m_left->m_col = Color::BLACK; //将这个红色的左孩子变黑即可
else if (delPos->m_right != nullptr) //待删除结点有一个红色的右孩子(不可能是黑色)
delPos->m_right->m_col = Color::BLACK; //将这个红色的右孩子变黑即可
else //待删除结点的左右均为空