启发式算法（heuristic algorithm)
Posted haohai9309
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了启发式算法（heuristic algorithm)相关的知识，希望对你有一定的参考价值。
运筹学--Operations Research (O.R.)，有时也称为数学规划、最优化理论，是人工智能的“引擎”，因为几乎所有人工智能的问题最后都会转化为求解优化问题。几年前流行的支持向量机（SVM，二次规划问题）如此，近几年席卷全球的深度学习（DL）的参数优化（训练）也是（高度复合函数无约束优化问题）。现今在社会经济管理、生命科学领域中，决策环境越来越复杂，众多因素有着错综复杂的相互作用，复杂的决策过程致使建立模型的难度越来越高，决策变量的量级、取值、目标的复杂多样、约束的非线性成程度都是经典优化算法难以求解的，这样启发式算法就应运而生。启发式算法通常是以问题为导向的（Problem Specific），也就是说，没有一个通用的框架，每个不同的问题通常设计一个不同的启发式算法，由于这些问题都是NP-Hard（要求得全局最优解通常需要指数级算法复杂度，不存在多项式时间算法）的，人们一般会根据特定的问题设计只针对该问题的启发式算法。
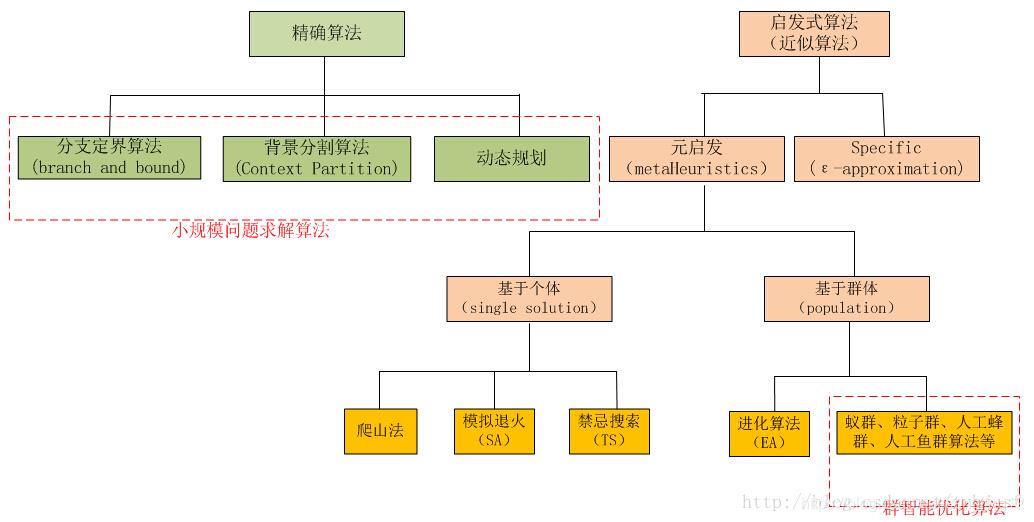
一、精确算法与启发式算法
1.1 数学最优化模型结构
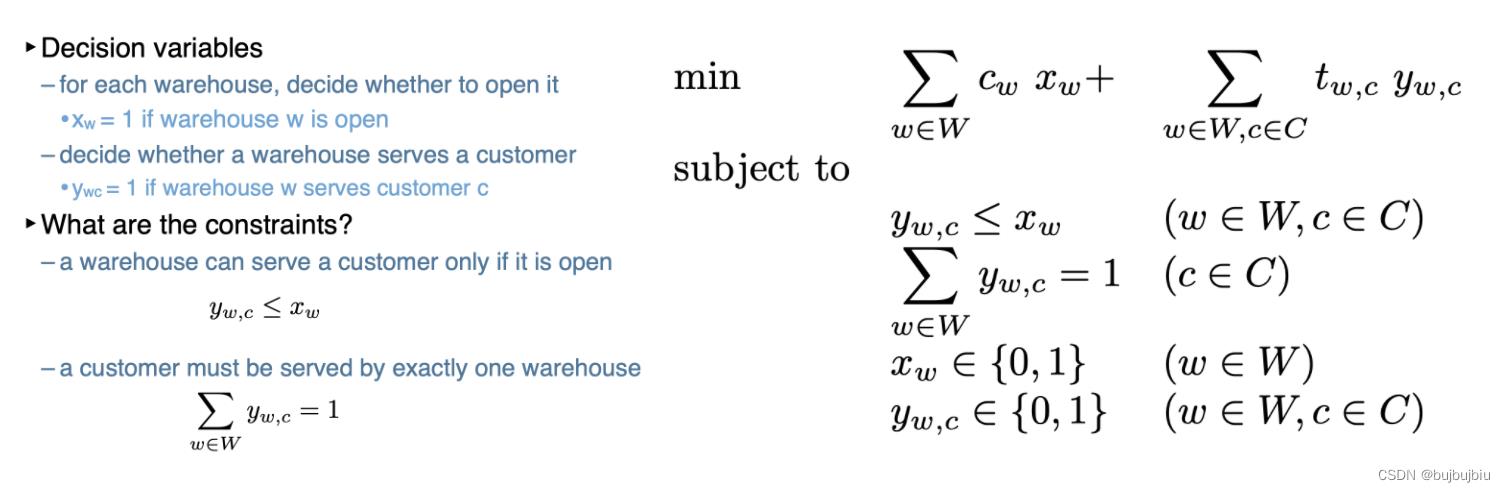
一般而言，算法所需要解决的问题，都能分成三个部分：
目标：什么是目标呢？简单点说就是要优化的东西，比如在上述背包问题中，要优化的就是所选物品的价值，使其最大。
决策：顾名思义就是根据目标所作出的决策，比如在这里就是决定选取哪些物品装进我们的背包。
约束：那么何又为约束呢？就是说再进行决策时必须遵循的条件，比如上面的背包问题，我们所选取的物品总的重量不能超过背包的容量。要是没有容量的约束，小学生才做选择呢，我全都要！
1.2 启发式算法
启发式算法是针对精确算法而言的。
精确算法：找到最优解并评估最优性，有严格的最优化数学理论支撑。到目前为止，已提出的精确算法种类较多，有单纯形法、分支定界法、割平面法、整数规划算法和动态规划算法等。一般可用软件为MATLAB，LINGO，Python等。(Exact optimization method> s (Jourdan et al, 2009): ‘Exact methods find the optimal solution and assess its optimality’.)
启发式算法（heuristic algorithm)：在问题结构不良的情况下，为得到近似可用的解，分析人员必须运用自己的感知和洞察力，从与其有关而较基本的模型及算法中寻求其间的联系，从中得到启发，去发现适于解决该问题的思路和途径，这种方法称为启发式方法。由此建立的算法称为启发式算法，可为复杂的优化问题快速生成近似最优解，许多启发式算法是相当特殊的，依赖于某个特定问题。启发式策略在一个寻求最优解的过程中能够根据个体或者全局的经验来改变其搜索路径，当寻求问题的最优解变得不可能或者很难完成时，启发式策略就是一个高效的获得可行解的办法。
启发式算法一般用于解决NP-hard问题，其中NP是指非确定性多项式。因为传统算法是把各种可能性都一一进行尝试，最终能找到问题的答案，但对于NP问题，传统算法花费几乎无穷的时间和算力才能求得答案。而启发式方法则限制了搜索空间，大大减少尝试的数量，能迅速地达到问题的解决。但由于这种方法具有尝试错误的特点，所以也有失败的可能性。
举个通俗易懂的例子：
驾驶汽车到达某人的家，写成算法是这样的：沿167 号高速公路往南行至Puyallup；从South Hill Mall 出口出来后往山上开 4.5 英里； 在一个杂物店旁边的红绿灯路口右转，接着在第一个路口左转；从左边褐色大房子的车道进去，就是North Cedar 路714 号。
用启发式方法来描述则可能是这样：找出上一次我们寄给你的信，照着信上面的寄出地址开车到这个镇；到了之后你问一下我们的房子在哪里。 这里每个人都认识我们——肯定有人会很愿意帮助你的；如果你找不到人，那就找个公共电话亭给我们打电话，我们会出来接你。
1.3 启发式算法特点
启发式算法一般用于解决NP-hard问题，例如，著名的推销员旅行问题（Travel Saleman Problem or TSP）：假设一个推销员需要从南京出发，经过广州，北京，上海，…，等 n 个城市， 最后返回香港。 任意两个城市之间都有飞机直达，但票价不等。假设公司只给报销 C 元钱，问是否存在一个行程安排，使得他能遍历所有城市，而且总的路费小于 C？推销员旅行问题显然是 NP 的。因为如果你任意给出一个行程安排，可以很容易算出旅行总开销。但是，要想知道一条总路费小于 C 的行程是否存在，在最坏情况下，必须检查所有可能的旅行安排。
启发式算法的基本特点： 复杂度不确定，但是在实际中往往也能得到一个比较好的效果。（1）随机初始可行解；（２）给定一个评价函数（常常与目标函数值有关）；（３）邻域，产生新的可行解；（４）选择和接受解得准则；（５）终止准则。 其中（４）集中反映了超启发式算法的克服局部最优的能力。
启发式算法目前缺乏统一、完整的理论体系，启发式算法的提出就是根据经验提出，没有什么坚实的理论基础。启发式算法中的参数对算法的效果起着至关重要的作用，如何有效设置参数是经验活但还要悟性，只有try again。启发算法缺乏有效的迭代停止条件。还是经验，迭代次数100不行，就200，还不行就1000，启发式算法收敛速度的研究等。应用启发式算法，你就知道没有完美的东西，要快你就要付出代价，就是越快你得到的解也就越差。启发式算法中，不能保证找到最佳解决方案，局部最优值的陷入无法避免。启发式本质上是一种贪心策略，这也在客观上决定了不符合贪心规则的更好（或者最优）解会错过。其特点是在解决问题时,利用过去的经验,选择已经行之有效的方法，而不是系统地、以确定的步骤去寻求答案。
二、启发式算法的发展
启发式算法的计算量都比较大，所以启发式算法伴随着计算机技术的发展，取得了巨大的成就。40年代：由于实际需要，人们已经提出了一些解决实际问题快速有效的启发式算法。50年代：启发式算法的研究逐步繁荣起来。随后，人们将启发式算法的思想和人工智能领域中的各种有关问题的求解的收缩方法相结合，提出了许多启发式的搜索算法。其中贪婪算法和局部搜索等到人们的关注。60年代: 随着人们对数学模型和优化算法的研究越来越重视，发现以前提出的启发式算法速度很快，但是解得质量不能保证。虽然对优化算法的研究取得了很大的进展，但是较大规模的问题仍然无能为力（计算量还是太大）。70年代：计算复杂性理论的提出。NP完全理论告诉我们，许多实际问题不可能在合理的时间范围内找到全局最优解。发现贪婪算法和局部搜索算法速度快，但解不好的原因主要是他们只是在局部的区域内找解，得到的解不能保证全局最优性。由此必须引入新的搜索机制和策略，才能有效地解决这些困难问题，这就导致了超启发式算法（meta-heuristic algorithms）的产生。
Holland模拟地球上生物进化规律提出了遗传算法（Genetic Algorithm），它的与众不同的搜索机制引起了人们再次引发了人们研究启发式算法的兴趣，从而掀起了研究启发式算法的热潮。80年代以后： 模拟退火算法（Simulated Annealing Algorithm），人工神经网络（Artificial Neural Network），禁忌搜索（Tabu Search）相继出现。最近，演化算法（Evolutionary Algorithm）, 蚁群算法（Ant Algorithms）， 拟人拟物算法，量子算法等油相继兴起，掀起了研究启发式算法的高潮。由于这些算法简单和有效，而且具有某种智能，因而成为科学计算和人类之间的桥梁。在一些寻找最优解问题中，传统的能够求出最优解的精确式算法（如分支界定、动态规划等）花费的时空过大。启发式算法（heuristic algorithm）是一种能以更快速度找出问题近似最优解的方法。启发式算法通过牺牲一些精度来换取较小的时空消耗，可以看作是解决问题的捷径。
三、常用的启发式算法
启发式算法的主要思想来自于人类经过长期对物理、生物、社会的自然现象仔细的观察和实践，以及对这些自然现象的深刻理解，逐步向大自然学习，模仿其中的自然现象的运行机制而得到的。
遗传算法(GA)：
遗传算法（Genetic Algorithm, GA）起源于对生物系统所进行的计算机模拟研究。它是模仿自然界生物进化机制发展起来的随机全局搜索和优化方法，借鉴了达尔文的进化论和孟德尔的遗传学说。其本质是一种高效、并行、全局搜索的方法，能在搜索过程中自动获取和积累有关搜索空间的知识，并自适应地控制搜索过程以求得最佳解。
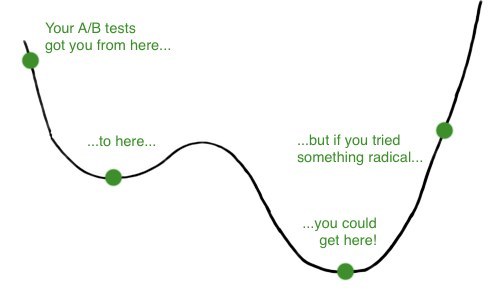
模拟退火算法(Simulated Annealing, SA)：
模拟退火算法的思想借鉴于固体的退火原理，当固体的温度很高的时候，内能比较大，固体的内部粒子处于快速无序运动，当温度慢慢降低的过程中，固体的内能减小，粒子的慢慢趋于有序，最终，当固体处于常温时，内能达到最小，此时，粒子最为稳定。模拟退火算法便是基于这样的原理设计而成。
蚁群算法(AG)：
蚁群算法是一种模拟蚂蚁觅食行为的模拟优化算法，它是由意大利学者Dorigo M等人于1991年首先提出，并首先使用在解决TSP（旅行商问题）上。 之后，又系统研究了蚁群算法的基本原理和数学模型.
粒子群优化算法（Particle Swarm Optimization, PSO）：
粒子群优化算法是一种基于鸟类觅食提出来的进化计算技术，由电气工程师Eberhart博士和美国社会心理学家Kennedy博士发明，是一种基于迭代的优化工具。该算法的基本思想是通过群体中个体之间的协作和信息共享来寻找最优解。由于没有遗传算法的交叉、变异，粒子群算法更容易实现
禁忌搜索算法TS（Tabu Search）
禁忌搜索由美国科罗拉多州大学的Fred Glover教授在1986年左右提出来的，是一个用来跳出局部最优的搜寻方法。 禁忌搜索是一种亚启发式随机搜索算法，它从一个初始可行解出发，选择一系列的特定搜索方向(移动)作为试探，选择实现让特定的目标函数值变化最多的移动。为了避免陷入局部最优解，TS搜索中采用了一种灵活的“记忆”技术，对已经进行的优化过程进行记录和选择，指导下一步的搜索方向。
这几种启发式算法都有一个共同的特点：从随机的可行初始解出发，才用迭代改进的策略，去逼近问题的最优解。
总结
在问题结构不良的情况下,为得到近似可用的解,分析人员必须运用自己的感知和洞察力,从与其有关而较基本的模型及算法中寻求其间的联系,从中得到启发,去发现适于解决该问题的思路和途径,这种方法称为启发式方法,由此建立的算法称为启发式算法。优点:(1)计算步骤简单,要求的理论基础不高,可由未经过高级训练的人员实现;(2)比优化方法常可减少大量的计算工作量,从而显著节约开支和时间;(3)易于将定量和定性分析相结合。不足:(1)不能保证求的最优解。(2)表现不稳定,启发式算法在同一问题的不同实例计算中会有不同的效果,有些很好,而有些则很差。在实际应用中,这种不稳定性造成计算结果不可信,可能造成管理的混乱。(3)算法的好坏依赖于实际问题,算法设计者的经验和技术,这点很难总结规律,同时使不同算法之间难以比较。
参考文献
启发式搜索（heuristic search）———A*算法
在宽度优先和深度优先搜索里面，我们都是根据搜索的顺序依次进行搜索，可以称为盲目搜索，搜索效率非常低。
而启发式搜索则大大提高了搜索效率，由这两张图可以看出它们的差别：
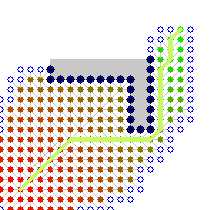（左图类似与盲搜，右图为启发式搜索）(图片来源)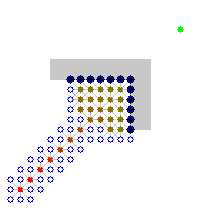 
很明显启发式的搜索效率远远大于盲搜。
什么是启发式搜索（heuristic search）
利用当前与问题有关的信息作为启发式信息，这些信息是能够提升查找效率以及减少查找次数的。
如何使用这些信息，我们定义了一个估价函数 h(x) 。h(x)是对当前状态x的一个估计，表示 x状态到目标状态的距离。
有：1、h(x) >= 0 ； 2、h(x)越小表示 x 越接近目标状态； 3、如果 h(x) ==0 ，说明达到目标状态。
与问题相关的启发式信息都被计算为一定的 h(x) 的值，引入到搜索过程中。
然而，有了启发式信息还不行，还需要起始状态到 x 状态所花的代价，我们称为 g(x) 。比如在走迷宫问题、八数码问题，我们的 g(x) 就是从起点到 x 位置花的步数 ，h(x) 就是与目标状态的曼哈顿距离或者相差的数目；在最短路径中，我们的 g(x) 就是到 x 点的权值，h(x) 就是 x 点到目标结点的最短路或直线距离。
现在，从 h(x) 和 g(x) 的定义中不能看出，假如我们搜索依据为 F(x) 函数。
当 F(x) = g(x) 的时候就是一个等代价搜索，完全是按照花了多少代价去搜索。比如 bfs，我们每次都是从离得近的层开始搜索，一层一层搜 ；以及dijkstra算法，也是依据每条边的代价开始选择搜索方向。
当F(x) = h(x) 的时候就相当于一个贪婪优先搜索。每次都是向最靠近目标的状态靠近。
人们发现，等代价搜索虽然具有完备性，能找到最优解，但是效率太低。贪婪优先搜索不具有完备性，不一定能找到解，最坏的情况下类似于dfs。
这时候，有人提出了A算法。令F(x) = g(x) + h(x) 。（这里的 h(x) 没有限制）。虽然提高了算法效率，但是不能保证找到最优解，不适合的 h(x)定义会导致算法找不到解。不具有完备性和最优性。
几年后有人提出了 A*算法。该算法仅仅对A算法进行了小小的修改。并证明了当估价函数满足一定条件，算法一定能找到最优解。估价函数满足一定条件的算法称为A*算法。
它的限制条件是 F(x) = g(x) + h(x) 。 代价函数g(x) >0 ；h(x) 的值不大于x到目标的实际代价 h*(x) 。即定义的 h(x) 是可纳的，是乐观的。
怎么理解第二个条件呢？
打个比方：你要从x走到目的地，那么 h(x) 就是你感觉或者目测大概要走的距离，h*(x) 则是你到达目的地后，发现你实际走了的距离。你预想的距离一定是比实际距离短，或者刚好等于实际距离的值。这样我们称你的 h(x) 是可纳的，是乐观的。
不同的估价函数对算法的效率可能产生极大的影响。尤其是 h(x) 的选定，比如在接下来的八数码问题中，我们选择了曼哈顿距离之和作为 h(x) ，你也可以选择相差的格子作为 h(x)，只不过搜索的次数会不同。当 h(x) 越接近 h*(x) ，那么扩展的结点越少！
那么A*算法的具体实现是怎么样的呢？
1、将源点加入open表
2、
while(OPEN!=NULL)
{
从OPEN表中取f(n)最小的节点n;
if(n节点==目标节点)
break;
for(当前节点n的每个子节点X)
{
计算f(X);
if(XinOPEN)
if(新的f(X)<OPEN中的f(X))
{
把n设置为X的父亲;
更新OPEN表中的f(n); //不要求记录路径的话可以直接加入open表，旧的X结点是不可能比新的先出队
}
if(XinCLOSE)
continue;
if(Xnotinboth)
{
把n设置为X的父亲;
求f(X);
并将X插入OPEN表中;
}
}//endfor
将n节点插入CLOSE表中;
按照f(n)将OPEN表中的节点排序;//实际上是比较OPEN表内节点f的大小，从最小路径的节点向下进行。
}//endwhile(OPEN!=NULL)
3、保存路径，从目标点出发，按照父节点指针遍历，直到找到起点。
以八数码问题为例：
我们从1、仅考虑代价函数； 2、仅考虑贪婪优先； 3、A*算法。
1 #include<bits/stdc++.h> 2 using namespace std; 3 struct Maze{ 4 char s[3][3]; 5 int i,j,fx,gx; 6 bool operator < (const Maze &a )const{ 7 return fx>a.fx; 8 } 9 } c; 10 int fx[4][2]={{-1,0},{1,0},{0,1},{0,-1}}; 11 map<char ,Maze > mp; 12 int T; 13 int get_hx(char s[3][3]){ 14 int hx=0; 15 for(int i=0;i<3;i++){ 16 for(int j=0;j<3;j++){ 17 hx+=abs(mp[s[i][j]].i-i)+abs(mp[s[i][j]].j-j); 18 } 19 } 20 return (int)hx; 21 } 22 void pr(char s[3][3]){ 23 cout<<"step: "<<T++<<endl; 24 for(int i=0;i<3;i++){ 25 for(int j=0;j<3;j++) 26 cout<<s[i][j]; 27 cout<<endl; 28 } 29 cout<<endl; 30 } 31 int key(char s[3][3]){ 32 int ans=0; 33 for(int i=0;i<3;i++) 34 for(int j=0;j<3;j++) 35 ans=ans*10+(s[i][j]-‘0‘); 36 return ans; 37 } 38 void BFS(){ 39 T=0; 40 map<int ,bool >flag; 41 queue < Maze > q; 42 q.push(c); 43 flag[key(c.s)]=1; 44 while(!q.empty()){ 45 Maze now=q.front(); 46 q.pop(); 47 pr(now.s); 48 if(get_hx(now.s)==0){ 49 break; 50 } 51 for(int i=0;i<4;i++){ 52 int x,y; 53 x=now.i+fx[i][0]; 54 y=now.j+fx[i][1]; 55 if(!(x>=0&&x<3&&y>=0&&y<3)) continue; 56 Maze tmp=now; 57 tmp.s[now.i][now.j]=tmp.s[x][y]; 58 tmp.s[x][y]=‘0‘; 59 tmp.i=x ; tmp.j=y ; 60 tmp.fx++; 61 if(!flag[key(tmp.s)]){ 62 q.push(tmp); 63 flag[key(tmp.s)]=1; 64 } 65 } 66 } 67 } 68 void Greedy_best_first_search(){ 69 T=0; 70 priority_queue< Maze > q ; 71 map<int ,int >flag; 72 c.fx=get_hx(c.s); 73 q.push(c); 74 flag[key(c.s)]=1; 75 while(!q.empty()){ 76 Maze now=q.top(); 77 q.pop(); 78 pr(now.s); 79 if(get_hx(now.s)==0){ 80 break; 81 } 82 for(int i=0;i<4;i++){ 83 int x,y; 84 x=now.i+fx[i][0]; 85 y=now.j+fx[i][1]; 86 if(!(x>=0&&x<3&&y>=0&&y<3)) continue; 87 Maze tmp=now; 88 tmp.s[now.i][now.j]=tmp.s[x][y]; 89 tmp.s[x][y]=‘0‘; 90 tmp.i=x ; tmp.j=y ; 91 tmp.fx=get_hx(tmp.s); 92 if(!flag[key(tmp.s)]){ 93 q.push(tmp); 94 flag[key(tmp.s)]=1; 95 } 96 } 97 } 98 } 99 void A_star(){ 100 T=0; 101 priority_queue< Maze > q ; 102 map<int ,int >flag; 103 c.gx=0; 104 c.fx=get_hx(c.s)+c.gx; 105 q.push(c); 106 while(!q.empty()){ 107 Maze now=q.top(); 108 q.pop(); 109 flag[key(now.s)]=now.fx; 110 pr(now.s); 111 if(get_hx(now.s)==0){ 112 break; 113 } 114 for(int i=0;i<4;i++){ 115 int x,y; 116 x=now.i+fx[i][0]; 117 y=now.j+fx[i][1]; 118 if(!(x>=0&&x<3&&y>=0&&y<3)) continue; 119 Maze tmp=now; 120 tmp.s[now.i][now.j]=tmp.s[x][y]; 121 tmp.s[x][y]=‘0‘; 122 tmp.i=x ; tmp.j=y ; 123 tmp.gx++; 124 tmp.fx=get_hx(tmp.s)+tmp.gx; 125 if(!flag[key(tmp.s)]){ 126 q.push(tmp); 127 }else if(flag[key(tmp.s)]>tmp.fx){ 128 flag[key(tmp.s)]=0; 129 q.push(tmp); 130 } 131 } 132 } 133 } 134 int main(){ 135 mp[‘1‘].i=0;mp[‘1‘].j=0; 136 mp[‘2‘].i=0;mp[‘2‘].j=1; 137 mp[‘3‘].i=0;mp[‘3‘].j=2; 138 mp[‘4‘].i=1;mp[‘4‘].j=2; 139 mp[‘5‘].i=2;mp[‘5‘].j=2; 140 mp[‘6‘].i=2;mp[‘6‘].j=1; 141 mp[‘7‘].i=2;mp[‘7‘].j=0; 142 mp[‘8‘].i=1;mp[‘8‘].j=0; 143 mp[‘0‘].i=1;mp[‘0‘].j=1; 144 for(int i=0;i<3;i++){ 145 for(int j=0;j<3;j++){ 146 cin>>c.s[i][j]; 147 } 148 char x=getchar(); 149 } 150 cin>>c.i>>c.j; 151 c.fx=0; 152 cout<<"八数码问题 BFS 解法(即仅以当前代价 g(x)搜索): "<<endl; 153 BFS(); 154 cout<<"八数码问题 Greedy_best_first_search 解法(即仅以估计函数 h(x)搜索): "<<endl; 155 Greedy_best_first_search(); 156 cout<<"八数码问题 A* 解法: "<<endl; 157 A_star(); 158 return 0; 159 } 160 /* 161 283 162 164 163 705 164 2 1 165 */
结果显示：
1、仅考虑代价函数：36步。
2、仅考虑贪婪优先：5步。
3、A*算法：5步。
明显，在引入了启发式信息后，大大的提高了搜索的效率。
引申问题： 第 k 短路问题。
思路： 先从终点求出最短路，作为 h(x) 。然后维护优先队列，维护 F(x) 最小，第一次出来的终点是最短路，终点第二次出来的是次短路……
求第k短路时，A*算法优化的是查找的次数，可以理解为剪枝，更快速的找到最短路，次短路……
其他操作和正常的求最短路没有什么区别，找到终点第k次出队的值，就是第k短路。
（可能你会说在无向图中存在有回头路，没错，有可能次短路只是最短路走了一次回头路，但这确实也是一条次短路）。
以上是关于启发式算法（heuristic algorithm)的主要内容，如果未能解决你的问题，请参考以下文章
ReactJS diff算法Part 2: React diff 启发式算法（heuristic algorithm）的假设
启发式搜索（heuristic search）———A*算法