LLVM 的DSA与APA优化
Posted 吴建明
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了LLVM 的DSA与APA优化相关的知识,希望对你有一定的参考价值。
LLVM在链接时所做的最激进的优化,莫过于DSA和APA。在DSA分析中,借助于LLVM比较充足的type information,在指针分析的基础上,可以构造出整个内存对象的连接关系图。然后对这个图进行分析,得到内存对象的连接模式,将连接比较紧密的结构对象,例如树、链表等结构体分配在自定义的一格连续分配的内存池中。这样可以少维护很多内存块,并且大大提高空间locality,相应的提高cache命中率。
APA(Automatic Pool Allocation)能够将堆上分配的链接形式的结构体,分配在连续的内存池中,这种做法是通过将内存分配函数替换为自定义池
分配函数实现的,示意图如下所示:
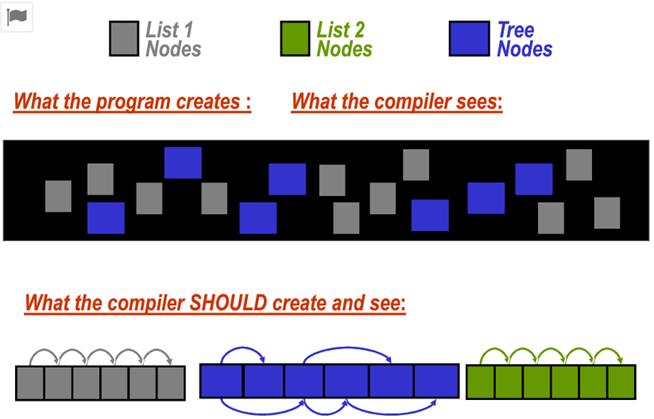
另外一些在链接阶段进行的分析,包括调用图构建,Mod/Ref分析,以及一些过程间的分析,例如函数inline,死全局变量删除(dead global elimination),死实参删除(dead argument),常量传播,列表边界检查消除(array bounds check elimination),简单结构体域重排(structure field reordering),以及Automatic Pool Allocation。
在编译时会汇总每个函数摘要信息(prodedure summary),附在LLVM IR中,在链接时就无需重新从源码中获取信息,直接使用函数摘要进行过程间分析即可。这种技术大大缩短了增量编译的时间。函数摘要一直是过程间分析的重点,因为这种技术在不过分影响精确性的前提下,大大提高了静态分析的效率。
这里简单提示一下,结构体域重排(structure field reordering)会涉及到以下问题:
1)为什么需要结构体域重排。
2)结构体域重排应该怎么做。
3)结构体域重排会不会带来其它影响。
另外结构体域重排,也可以与hot概念相结合,如下代码所示:
// s has hot member and cold member
struct s
char c;
int i;
double d;
;
// we can split s to two struct
struct hots
char c;
double d;
;
struct colds
int i;
;
将结构体根据hot的程度分拆成两个结构体,可以针对两个结构体进行不同的优化,例如,将hot结构体的member提升到register中等。
与结构体域重排优化概念相关的另外概念是padding,alignment,point compression。前两个概念与结构体域重排直接相关,示意代码如下所示:
struct s1
char a; // here padding 3 bytes
int b;
char c;
char d;
xhar e; // here padding 1 bytes
这个结构体的sizeof是12bytes,但是,如果将这个s1结构体子域重排的话,8bytes就够了,如下图所示:
struct s1
char a;
char c;
char d;
char e;
int b;
首先就是,要做reordering的前提就是,必须能够确保当前结构体只在当前TU中,如果当前结构体在另外的TU中也存在的话,那么就会存在结构体内存布局不相容的情况。所以这样的优化只能在链接时进行。
另外,就是要相应修改所有对struct进行引用的操作,在C/C++这些类型不安全的语言中,类型转换非常普遍,有可能另外一种类型的使用其实就是在当前类型那个内存上进行的,如下代码所示。如何识别跟踪这些类型转换是一格非常困难的问题,LLVM IR提供了type information来帮助执行这些优化。
struct s
char a;
int b;
char c;
;
struct s_head
char a;
;
struct s_ext
char a;
int b;
char c;
int d;
char e;
;
struct S s;
struct S_head *head = (struct S_head*)&s;
fn1(head);
struct S_ext ext;
struct S *sp = (struct S*)&ext;
fn2(sp);
另一个与reordering the fields相关的概念就是point compression,这两者的目的都是用于提高内存使用率,使内存显得更为紧凑。与reordering hte fields类似的两个优化概念是Structure peeling,structure splitting,这些都属于Data Layout Optimizations。
LLVM代码生成器
在寄存器分配之前,LLVM会一直保存SSA形式。LLVM代码生成结构如下图所示:
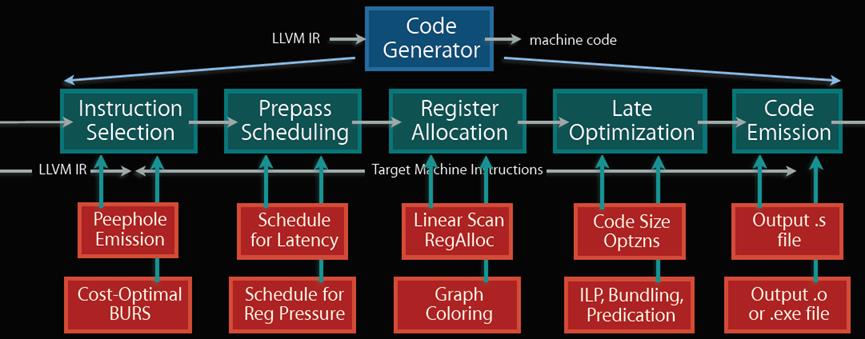
图中描述了在代码生成时用到的一些技术。
装载时优化
运行时优化
在大部分人看来,运行时优化仅仅与JIT、虚拟机和CPU乱序发射以及cache相关,因为运行时优化只在运行时执行,JIT可以结合虚拟机在程序解释执行时识别出hot区域,以便能够将这些代码编译成native code,CPU乱序可以依据当前指令的相关性来执行指令重排等操作,而cache也可以将频繁出现的内容缓存到cache中以便加快执行速度。可是,LLVM与这些貌似都无关,确实LLVM运行时优化与他们不相同。LLVM运行时优化与闲时优化相互结合来实现相关优化,LLVM会在代码生成的时候插入一些低代价的指令来收集运行时的信息(profiling information),这些信息用于指导闲时优化重新生成一份更加高效的native code。这个过程也可以重复多次来达到较优的效果。一个重要的用处就是识别hot loop region和hot path,然后再对这些热区域进行特殊处理。
数据结构与算法笔记 - 绪论
数据结构与算法笔记 - 绪论
1. 什么是计算
2. 评判DSA优劣的参照(直尺)
3. 度量DSA性能的尺度(刻度)
4. DSA的性能度量的方法
5. DSA性能的设计及其优化
x1. 理论模型与实际性能的差异
x2. DSA优化的极限(下界)
计算机与算法
计算机科学(computer science)的核心在于研究计算方法与过程的规律,而不仅仅是作为计算工具的计算机本身,因此E. Dijkstra及其追随者更倾向于将这门科学称作计算科学(computing science)。
计算 = 信息处理
计算模型 = 计算机 = 信息处理工具
1. 计算机的本质是计算,计算是寻找对象的规律,并从中找到技巧。计算的目标是高效,低耗。
2. 算法就是借助一定的工具,在一定的规则下,以明确而机械的形式来进行的计算。
算法定义:基于特定的计算类型,旨在解决某一信息处理问题而设计的一个指令序列。
3. 算法需具备以下要素
输入与输出
输入(input):对所求解问题特定实例的描述
输出(output):经计算和处理之后得到的信息,即针对输入问题实例的答案
确定性和可行性:算法应可描述为由若干语义明确的基本操作组成的指令序列,且每一基本操作在对应的计算模型中均可兑现。
有穷性:任意算法都应在执行有限次基本操作之后终止并给出输出
正确性:算法所给的输出应该能够符合由问题本身在事先确定的条件
退化和鲁棒性:例如算法数据的各种极端的输入实例都属于退化(degeneracy)情况,鲁棒性(robustness)要求尽可能充分地应对此类情况。
重用性:算法模式可推广并适用于不同类型基本元素的特性
证明算法的有穷性和正确性:从适当的角度审视整个计算过程,找出其所具有的某种不变性和单调性。
单调性:问题的有效规模会随着算法的推进不断递减
不变性:不仅应在算法初始状态下自然满足,而且应与最终的正确性相呼应----当问题的规模缩减到0时,不变性应随即等价于正确性
例如, 冒泡排序的正确性证明:(不变性)经过k趟扫描交换后,最大的前k个元素必然就位;(有穷性)经过k趟扫描交换后,待求解问题的有效规模将缩减至n-k。
好的算法:效率最高(速度尽可能快,存储空间尽可能少)同时又兼顾正确(算法能够正确地解决问题)、健壮(容错性好)、可读(易于阅读)。 类似既要马儿跑的快,又要吃的少。
算法 + 数据结构 = 程序 (算法 + 数据结构) * 效率 = 计算
计算模型
1. 一个好的程序不仅要考虑数据结构与算法,还要考虑效率,即:(数据结构+算法)*效率 = 程序 => 应用。
2. 算法分析的两个重要指标 (需要进行度量)
正确性:算法功能是否与问题一致
成本:时间消耗与存储空间消耗
3. 定义:T(n) 为一个算法在最坏的情况下所需要操作的步骤。不同算法之间的好坏主要看T(n)的大小,T(n)是屏蔽了计算机硬件差异,语言差异,编译差异等差异之后的理想平台下的运行指标,如大O,大Ω,大Θ等。
4. 一般的计算模型有图灵模型与RAM模型,它们均将算法的运算时间转换成算法执行的基本操作次数。
图灵机模型
图灵机的三个组成要件
1. 有限的字母表: cell中存储的内容
2. 读写头: 只是当前位置, 可读可写
3. 状态表: 当前读写头的状态
图灵机状态转换过程 transform(q,c; d,L/R,p)
q:当前状态
c:读写头所指cell当前的内容
d:读写头所指cell改写的内容
L/R:向左/右移位
p:读写头转换后的状态

RAM 模型
1. 与图灵机类似,均假设有无限空间
2. 由一系列顺序编号寄存器组成,但总数无限
3. 算法所运行的时间转换成算法运算时的次数

数据结构
数据结构示意
数据对象由数据元素组成,数据元素由数据项组成,数据项是最基本的单位
数据结构指数据对象中数据元素之间的关系
数据结构主要研究非数值计算程序问题中的操作对象以及它们之间的关系
数据结构的逻辑结构
集合结构
线性结构
树结构
图结构
数据结构的物理结构
顺序存储结构
链式存储结构
数据的运算
插入
删除
修改
查找
排序
复杂度度量
1. 算法的效率主要看时间消耗与存储空间消耗,这里我们屏蔽存储空间的消耗,仅仅考虑时间的消耗。
2. 大O的定义:T(n)=O(f(n)) ,f(n)为一个函数。当c>0,T(n)<c∗f(n),即大O记号表示T(n)的一个上界,其性质为:
O(n)=O(c∗n)
O(n^2+n)=O(n^2)
3. 大Ω的定义:T(n)=Ω(f(n)) ,f(n)为一个函数。当c>0,T(n)>c∗f(n),即大O记号表示T(n)的一个下界。
4. 大Θ的定义:T(n)=Θ(f(n)) ,f(n)为一个函数。当c1>c2>0,c1∗f(n)>T(n)>c2∗f(n),即大O记号表示T(n)的一个区间。
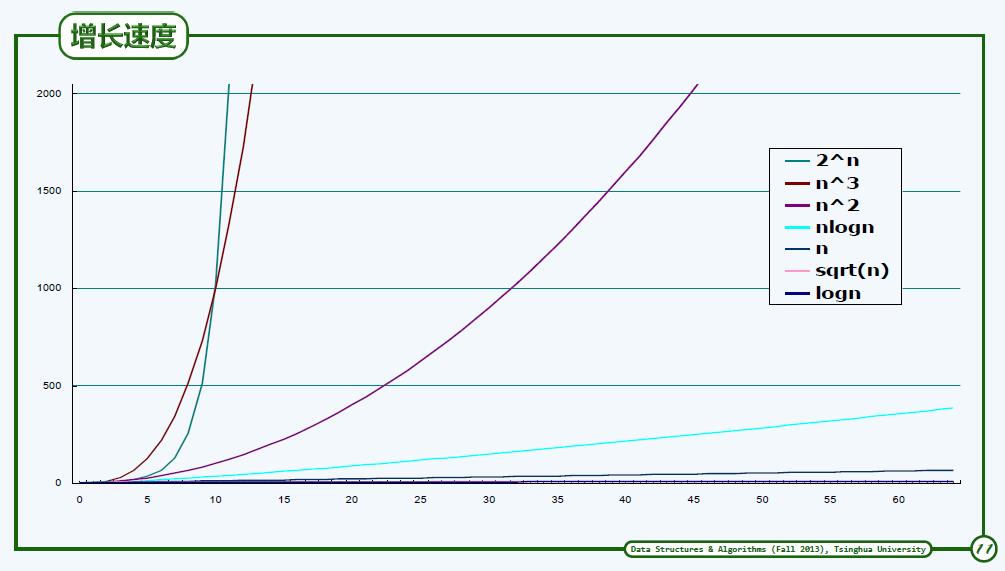
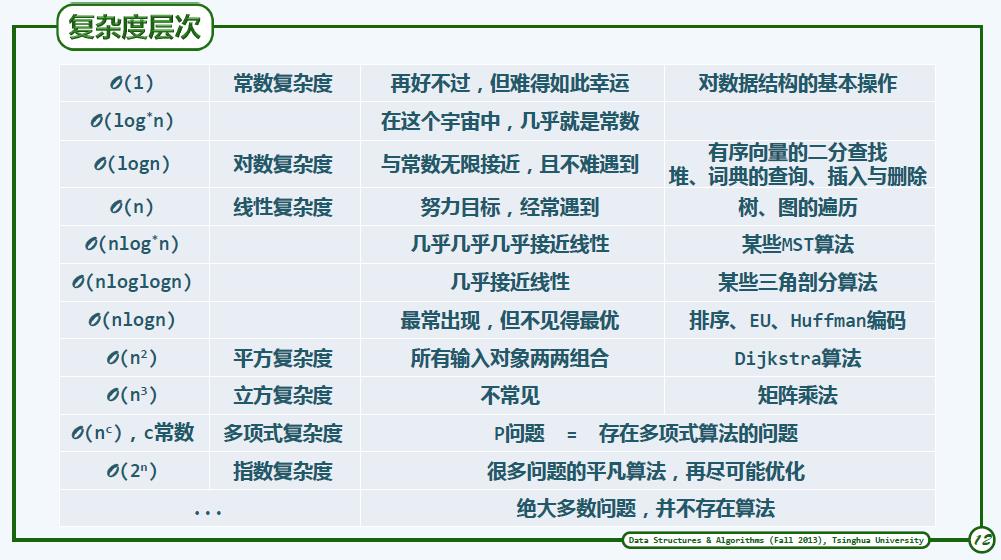
5. 大O记号的分类:
常数类:O(1)=2 or222222 ,有效
对数类:O(log^c n)与常底数、常数次幂无关,复杂度接近常数,有效。
多项式:O(n^c)
线性:O(n)
指数:c^n=O(2^n)任何c均可。成本增长极快,不是有效的。
6. 时间复杂度T(n) :特定算法处理规模为n的问题所需的时间,由于n相同,但T(n)不同,---->简化为:
在规模为n的所有输入中选择时间最长者作为T(n),并以T(n)度量算法的时间复杂度。
7. 渐进时间复杂度:注重时间复杂度随问题规模n的增长的总体变化趋势
大O记号(T(n)的渐进上界):
若存在正的常数c和函数f(n),使的对任何n>>2都有: T(n) <= c * f(n),即认为在n足够大之后,f(n)给出了T(n)增长速度的一个渐进上界,记为:T(n) = O( f(n) )
8. 大O记号性质:
对于任一常数 c > 0, 有O( f(n) ) = O( c * f(n) ):在大O记号意义下:函数各项正的常系数可以忽略并等同于1
对于任意常数 a > b > 0,有 O( n ^ a + n ^ b ) = O( n ^ a ):在大O记号意义下:多项式中的低次项均可忽略
9. 空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度。一个算法在计算机存储器上所占用的存储空间,包括存储算法本身所占用的存储空间,算法的输入输出数据所占用的存储空间和算法在运行过程中临时占用的存储空间这三个方面。
算法的空间复杂度通过计算算法所需的存储空间实现,算法空间复杂度的计算公式记作:S(n)= O(f(n)),其中,n为问题的规模,f(n)为语句关于n所占存储空间的函数。
一般情况下,一个程序在机器上执行时,除了需要存储程序本身的指令、常数、变量和输入数据外,还需要存储对数据操作的存储单元。若输入数据所占空间只取决于问题本身,和算法无关,这样只需要分析该算法在实现时所需的辅助单元即可。若算法执行时所需的辅助空间相对于输入数据量而言是个常数,则称此算法为原地工作,空间复杂度为O(1)。
关于O(1)的问题, O(1)是说数据规模和临时变量数目无关,并不是说仅仅定义一个临时变量。举例:无论数据规模多大,我都定义100个变量,这就叫做数据规模和临时变量数目无关。就是说空间复杂度是O(1)。
当一个算法的空间复杂度为一个常量,即不随被处理数据量n的大小而改变时,可表示为O(1);当一个算法的空间复杂度与以2为底的n的对数成正比时,可表示为0(10g2n);当一个算法的空I司复杂度与n成线性比例关系时,可表示为0(n).若形参为数组,则只需要为它分配一个存储由实参传送来的一个地址指针的空间,即一个机器字长空间;若形参为引用方式,则也只需要为其分配存储一个地址的空间,用它来存储对应实参变量的地址,以便由系统自动引用实参变量。
10. 对于一个算法,其时间复杂度和空间复杂度往往是相互影响的。当追求一个较好的时间复杂度时,可能会使空间复杂度的性能变差,即可能导致占用较多的存储空间;反之,求一个较好的空间复杂度时,可能会使时间复杂度的性能变差,即可能导致占用较长的运行时间。另外,算法的所有性能之间都存在着或多或少的相互影响。因此,当设计一个算法(特别是大型算法)时,要综合考虑算法的各项性能,算法的使用频率,算法处理的数据量的大小,算法描述语言的特性,算法运行的机器系统环境等各方面因素,才能够设计出比较好的算法。
11. 通常,我们都使用“时间复杂度”来指运行时间的需求,使用“空间复杂度”指空间需求。当不用限定词地使用“复杂度”时,通常都是指时间复杂度。
算法分析
1. 算法分析主要有两个任务:
正确性
复杂度
2. 复杂度的分析方法有三种:
迭代式算法:级数求和
递归式算法:递归跟踪 + 递归方程
猜测 + 验证
3. 算数级数:与末项的平方同阶
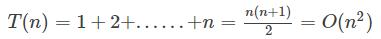
4. 幂方级数:比幂次高出一阶
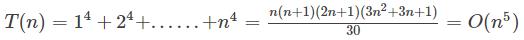
5. 几何级数(a>1):与末项同阶
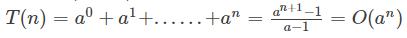
6. 收敛级数:O(1)
7. 可能未必收敛,但长度有限
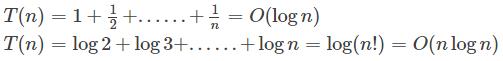
8. 循环:一般随着层数的增加指数式增长
9. 递归跟踪分析:检查每个递归实例,累计所需时间(调入语句本身,计入对应的子实例),总和即为算法执行时间。
迭代与递归
算法的两种思想方法:分而治之,减而治之。
分而治之:将一个问题分两个规模大小差不多的子问题。
减而治之:将一个问题分为一个子问题和一个规模缩减的问题。
#define _CRT_SECURE_NO_WARNINGS #include <iostream> #include <string> #include <algorithm> // 问题: 计算任意n个整数之和 // 实现: 使用迭代的方法, 逐一取出每个元素, 累加之 // 时间复杂度: T(n) = 1 + n * 1 + 1 = n + 2 = O(n) // 空间复杂度: S(n) = 1 + 1 = 2 = O(1) int SumA(int A[], int n) { int sum = 0; for (int i = 0; i < n; i++) { sum += A[i]; } return sum; } // 实现: 使用线性递归的方法 // 时间复杂度: T(n) = O(1) * (n+1) = O(n) // 空间复杂度: S(n) = O(1) * (n+1) = O(n) int SumB(int A[], int n) { return (1 > n) ? 0 : A[n-1] + SumB(A, n-1); } // 实现: 二分递归的方法 // 时间复杂度: T(n) = O(1) * (2^0 + 2^1 + 2^2 + ... + 2^log.n) = O(1) + (2^log.(n+1) -1) = O(n) // 空间复杂度: S(n) = O(1) * (2^0 + 2^1 + 2^2 + ... + 2^log.n) = O(1) + (2^log.(n+1) -1) = O(n) int SumC(int A[], int lo, int hi) // 区间范围A[lo, hi] 调用方式为SumC(A, 0, n -1) { if (lo == hi) // 如遇递归基(区间长度已降至1), 则 { return A[lo]; // 直接返回改元素 } else // 否则 ( 一般情况下 lo < hi ), 则 { int mi = (lo + hi) >> 1; // 以居中单元为界,将原区间一分为二 return SumC(A, lo, mi) + SumC(A, mi + 1, hi); // 递归对各个子数组求和, 然后合计 } } // 任给数组A[0, n), 降其前后颠倒 // 实现: 使用递归的方法 // 时间复杂度: T(n) = (hi - lo) / 2 = n/2 = O(n) // 空间复杂度: S(n) = O(n) void reverseA(int A[], int lo, int hi) // 区间范围A[lo, hi] 调用方式为reverseA(A, 0, n -1) { if (lo < hi) { // std::swap 需要引入 algorithm 头文件 // 问题规模的奇偶性不变, 需要两个递归基 std::swap(A[lo], A[hi]); // 交换A[lo]和A[hi] reverseA(A, lo+1, hi-1); //递归倒置 A(lo, hi) } else // 隐含了两种递归基 { return; } } // 任给数组A[0, n), 降其前后颠倒 // 实现: 使用迭代的方法 // 时间复杂度: T(n) = (hi - lo) / 2 = n/2 = O(n) // 空间复杂度: S(n) = O(1) void reverseB(int A[], int lo, int hi) // 区间范围A[lo, hi] 调用方式为reverseA(A, 0, n -1) { while (lo < hi) // 用while替换跳转标志和if,完全等效 { std::swap(A[lo++], A[hi--]); // 交换A[lo]和A[hi],收缩待倒置匙间 } } int main() { int iArray[] = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20}; std::cout << SumA(iArray, sizeof(iArray)/sizeof(iArray[0])) << std::endl; // 210 std::cout << SumB(iArray, sizeof(iArray)/sizeof(iArray[0])) << std::endl; // 210 std::cout << SumC(iArray, 0, sizeof(iArray)/sizeof(iArray[0]) - 1) << std::endl; // 210 reverseA(iArray, 0, sizeof(iArray)/sizeof(iArray[0]) - 1); // 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 for (auto a : iArray) { std::cout << a << " "; } std::cout << std::endl; reverseB(iArray, 0, sizeof(iArray)/sizeof(iArray[0]) - 1); // 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 for (auto a : iArray) { std::cout << a << " "; } std::cout << std::endl; system("pause"); return 0; }
动态规划
1. 动态规划的目的:
make it work(递归可以保证)
make it right(递归可以保证)
make it fast(迭代可以保证)
2. 递归对于资源的消耗大而且O(n)比较大,然而迭代可以降低对存储空间的使用,有时亦可以降低O(n)
3. 子序列:由原序列中若干个元素,按原来相对次序排列而成的新的序列。
4. 最长公共子序列(longest common subsequence, LCS)是两个序列中,在其相同的子序列中长度最长的那个子序列,可能含有多个。
动态规划的方法改良Fib的算法:
int fib (int n) { int i =1, f = 0, g = 1; while(++i < n/2) { f = f + g; //计算奇数项 g = f + g; //计算偶数项 } return(n % 2) ? f: g; //n为奇数时返回f,偶数时返回g }
递归版最长公共子串:
int lcs (string a, string b) { int m,n; m =a.size(); n =b.size(); stringc, d; for (inti = 0; i < m - 1; i++) //取a串的(m-1)个字符 c[i] = a[i]; for (intj = 0; j < n - 1; j++) //取b串的(n-1)个字符 d[j] = b[j]; if (a[m-1]== b[n-1]) return lcs(c, d) + 1; //当a[m-1]等于b[n-1]时,长度计数加一 else return (lcs(a,d) > lcs (b,c)) ? lcs(a, d): lcs(b, c);//当两个子串的lcs长度不同时,长度计数取更大者 }
使用动态规划的思想求解最长公共子串:
int lcs (string a, string b, const int m,const int n) //m=a.size()+1, n=b,size()+1 { intacc[m][n] = { 0 }; inti, j for(i = 1; i < m - 1; i++) for(j = 1; j < n - 1; j++) { if(acc[i][j-1] == acc[i-1][j]) { if(a[i] == b[j]) acc[i][j]= acc[i][j-1] + 1; //当a[i]等于b[j]时,长度计数加一 else acc[i][j]= acc[i][j-1]; //当二者不等时,长度计数不变 } else acc[i][j]= (acc[i][j-1] > acc[i-1][j]) ? acc[i][j-1]: acc[i-1][j];//当两个子串的lcs长度不同时,长度计数取更大者 } }
Fib() 递归方程的封底估算
FLOPS(即“每秒浮点运算次数”,“每秒峰值速度”),是“每秒所执行的浮点运算次数”(floating-point operations per second)的缩写。它常被用来估算电脑的执行效能,尤其是在使用到大量浮点运算的科学计算领域中。正因为FLOPS字尾的那个S,代表秒,而不是复数,所以不能省略掉。
在这里所谓的“浮点运算”,实际上包括了所有涉及小数的运算。这类运算在某类应用软件中常常出现,而它们也比整数运算更花时间。现今大部分的处理器中,都有一个专门用来处理浮点运算的“浮点运算器”(FPU)。也因此FLOPS所量测的,实际上就是FPU的执行速度。而最常用来测量FLOPS的基准程式(benchmark)之一,就是Linpack。
1GHz 就是每秒十亿次(=10^9)运算,如果每次运算能完成两个浮点操作,就叫 2G FLOPS(每秒二十亿次浮点操作)。现在家用的双核计算机通常都能达到每秒四十亿次运算(2*2.0GHz)左右的水平,浮点性能大约是上百亿次(=10^10)浮点操作。

__int64 Fib::fib(int n) // 计算Fibonacci数列的第n项(二分递归版):O(2^n) { return ( 2 > n ) ? ( __int64 ) n // 若到达递归基,直接取值 : fib ( n - 1 ) + fib ( n - 2 ); // 否则,递归计算前两项,其和即为正解 }
printf ( "\\n------------- Binary Recursion -------------\\n" ); for (int i = 0; i < n; i++) { start = clock(); printf("fib(%2d) = %22I64d\\n", i, f.fib(i)); // T(n) = O(2^n) finish = clock(); duration = (double)(finish - start) / CLOCKS_PER_SEC; printf(">>> Time: %2.3f seconds\\n", duration); }
计算f(35)所需的时间
------------- Binary Recursion ------------- fib( 0) = 0 >>> Time: 0.000 seconds fib( 1) = 1 >>> Time: 0.000 seconds fib( 2) = 1 >>> Time: 0.000 seconds fib( 3) = 2 >>> Time: 0.000 seconds fib( 4) = 3 >>> Time: 0.000 seconds fib( 5) = 5 >>> Time: 0.000 seconds fib( 6) = 8 >>> Time: 0.000 seconds fib( 7) = 13 >>> Time: 0.000 seconds fib( 8) = 21 >>> Time: 0.000 seconds fib( 9) = 34 >>> Time: 0.000 seconds fib(10) = 55 >>> Time: 0.000 seconds fib(11) = 89 >>> Time: 0.000 seconds fib(12) = 144 >>> Time: 0.000 seconds fib(13) = 233 >>> Time: 0.000 seconds fib(14) = 377 >>> Time: 0.000 seconds fib(15) = 610 >>> Time: 0.000 seconds fib(16) = 987 >>> Time: 0.000 seconds fib(17) = 1597 >>> Time: 0.000 seconds fib(18) = 2584 >>> Time: 0.000 seconds fib(19) = 4181 >>> Time: 0.000 seconds fib(20) = 6765 >>> Time: 0.000 seconds fib(21) = 10946 >>> Time: 0.000 seconds fib(22) = 17711 >>> Time: 0.000 seconds fib(23) = 28657 >>> Time: 0.000 seconds fib(24) = 46368 >>> Time: 0.015 seconds fib(25) = 75025 >>> Time: 0.016 seconds fib(26) = 121393 >>> Time: 0.015 seconds fib(27) = 196418 >>> Time: 0.032 seconds fib(28) = 317811 >>> Time: 0.046 seconds fib(29) = 514229 >>> Time: 0.094 seconds fib(30) = 832040 >>> Time: 0.125 seconds fib(31) = 1346269 >>> Time: 0.218 seconds fib(32) = 2178309 >>> Time: 0.359 seconds fib(33) = 3524578 >>> Time: 0.562 seconds fib(34) = 5702887 >>> Time: 1.092 seconds fib(35) = 9227465 >>> Time: 1.542 seconds fib(36) = 14930352 >>> Time: 2.477 seconds fib(37) = 24157817 >>> Time: 4.007 seconds fib(38) = 39088169 >>> Time: 6.281 seconds fib(39) = 63245986 >>> Time: 10.394 seconds fib(40) = 102334155 >>> Time: 17.638 seconds fib(41) = 165580141 >>> Time: 36.837 seconds fib(42) = 267914296 >>> Time: 52.502 seconds Return Value: 0 请按任意键继续. . .
Ο(1)表示基本语句的执行次数是一个常数,一般来说,只要算法中不存在循环语句,其时间复杂度就是Ο(1)。其中Ο(log2n)、Ο(n)、 Ο(nlog2n)、Ο(n2)和Ο(n3)称为多项式时间,而Ο(2n)和Ο(n!)称为指数时间。计算机科学家普遍认为前者(即多项式时间复杂度的算法)是有效算法,把这类问题称为P(Polynomial,多项式)类问题,而把后者(即指数时间复杂度的算法)称为NP(Non-Deterministic Polynomial, 非确定多项式)问题。
Fibonacci 部分的测试源代码及测试输出:
/* Start of Fib.h */ #ifndef __FIB_H__ #define __FIB_H__ class Fib // Fibonacci数列类 { private: int f, g; // f = fib(k - 1), g = fib(k)。均为int型,很快就会数值溢出 public: Fib(int n); // 初始化为不小于n的最小Fibonacci项 int get(); // 获取当前Fibonacci项,O(1)时间 int next(); // 转至下一Fibonacci项,O(1)时间 int prev(); // 转至上一Fibonacci项,O(1)时间 __int64 fibI(int n); // 计算Fibonacci数列的第n项(迭代版):O(n) __int64 fib(int n); // 计算Fibonacci数列的第n项(二分递归版):O(2^n) __int64 fib(int n, __int64 & prev); // 计算Fibonacci数列第n项(线性递归版):入口形式fib(n, prev) }; #endif // !__FIB_H__ /* End of Fib.h */
/* Start of Fib.cpp */ #include "Fib.h" // fib(-1), fib(0),O(log_phi(n))时间 Fib::Fib(int n) { f = 1; g = 0; while (g < n) { next(); } } __int64 Fib::fibI(int n) // 计算Fibonacci数列的第n项(迭代版):O(n) { __int64 f = 1, g = 0; while (0 < n--) { // 依据原始定义,通过n次加法和减法计算fib(n) g += f; f = g - f; } return g; } __int64 Fib::fib(int n) // 计算Fibonacci数列的第n项(二分递归版):O(2^n) { return ( 2 > n ) ? ( __int64 ) n // 若到达递归基,直接取值 : fib ( n - 1 ) + fib ( n - 2 ); // 否则,递归计算前两项,其和即为正解 } __int64 Fib::fib(int n, __int64 & prev) // 计算Fibonacci数列第n项(线性递归版):入口形式fib(n, prev) { if ( 0 == n ) // 若到达递归基,则 { prev = 1; return 0; } // 直接取值:fib(-1) = 1, fib(0) = 0 else { // 否则 __int64 prevPrev; prev = fib(n - 1, prevPrev ); // 递归计算前两项 return prevPrev + prev; //其和即为正解 } } // 用辅助变量记录前一项,返回数列的当前项,O(n) // 获取当前Fibonacci项,O(1)时间 int Fib::get() { return g; } // 转至下一Fibonacci项,O(1)时间 int Fib::next() { g += f; f = g - f; return g; } // 转至上一Fibonacci项,O(1)时间 int Fib::prev() { f = g -f; g -= f; return g; } /* End of Fib.cpp */
/* Start of mytest.cpp */ #define _CRT_SECURE_NO_WARNINGS #include <iostream> #include <string> #include <ctime> #include <algorithm> #include "Fib.h" int mytest(int argc, char * argv[]) { // clock_t实际为long类型 // 常量CLOCKS_PER_SEC 表示每一秒(per second)有多少个时钟计时单元 clock_t start, finish; double duration; int n = 36; // Rank Value // 检查参数 if (2 > argc) { fprintf ( stderr, "Usage: %s <rank>\\n", argv[0] ); } else { n = atoi(argv[1]); } // 依次计算Fibonacci数列各项 Fib f(0); start = clock(); printf("\\n------------- class Fib -------------\\n"); for (int i = 0; i < n; i++, f.next()) { printf( "fib(%2d) = %d\\n", i, f.get()); // T(n) = O(n) } finish = clock(); duration = (double)(finish - start) / CLOCKS_PER_SEC; printf(">>> Time: %2.3f seconds\\n", duration); start = clock(); for (int i = 0; i <= n; i++, f.prev()) { printf ("fib(%2d) = %d\\n", n - i, f.get()); // T(n) = O(n) } finish = clock(); duration = (double)(finish - start) / CLOCKS_PER_SEC; printf(">>> Time: %2.3f seconds\\n", duration); start = clock(); printf ("\\n------------- Iteration -------------\\n"); for (int i = 0; i < n; i++) { printf("fib(%2d) = %22I64d\\n", i, f.fibI(i)); // T(n) = O(n^2) } finish = clock(); duration = (double)(finish - start) / CLOCKS_PER_SEC; printf(">>> Time: %2.3f seconds\\n", duration); start = clock(); printf ( "\\n------------- Linear Recursion -------------\\n" ); for (int i = 0; i < n; i++) { __int64 fp; printf ( "fib(%2d) = %22I64d\\n", i, f.fib(i, fp)); // T(n) = O(n^2) } finish = clock(); duration = (double)(finish - start) / CLOCKS_PER_SEC; printf(">>> Time: %2.3f seconds\\n", duration); start = clock(); printf ( "\\n------------- Binary Recursion -------------\\n" ); for (int i = 0; i < n; i++) { printf("fib(%2d) = %22I64d\\n", i, f.fib(i)); // T(n) = O(2^n) } finish = clock(); duration = (double)(finish - start) / CLOCKS_PER_SEC; printf(">>> Time: %2.3f seconds\\n", duration); return 0; } int main(int argc, char * argv[]) { std::cout << "\\nReturn Value: " << mytest(argc, argv) << std::endl; system("pause"); return 0; } /* End of mytest.cpp */
运行输出:
------------- class Fib ------------- fib( 0) = 0 fib( 1) = 1 fib( 2) = 1 fib( 3) = 2 fib( 4) = 3 fib( 5) = 5 fib( 6) = 8 fib( 7) = 13 fib( 8) = 21 fib( 9) = 34 fib(10) = 55 fib(11) = 89 fib(12) = 144 fib(13) = 233 fib(14) = 377 fib(15) = 610 fib(16) = 987 fib(17) = 1597 fib(18) = 2584 fib(19) = 4181 fib(20) = 6765 fib(21) = 10946 fib(22) = 17711 fib(23) = 28657 fib(24) = 46368 fib(25) = 75025 fib(26) = 121393 fib(27) = 196418 fib(28) = 317811 fib(29) = 514229 fib(30) = 832040 fib(31) = 1346269 fib(32) = 2178309 fib(33) = 3524578 fib(34) = 5702887 fib(35) = 9227465 >>> Time: 0.000 seconds fib(36) = 14930352 fib(35) = 9227465 fib(34) = 5702887 fib(33) = 3524578 fib(32) = 2178309 fib(31) = 1346269 fib(30) = 832040 fib(29) = 514229 fib(28) = 317811 fib(27) = 196418 fib(26) = 121393 fib(25) = 75025 fib(24) = 46368 fib(23) = 28657 fib(22) = 17711 fib(21) = 10946 fib(20) = 6765 fib(19) = 4181 fib(18) = 2584 fib(17) = 1597 fib(16) = 987 fib(15) = 610 fib(14) = 377 fib(13) = 233 fib(12) = 144 fib(11) = 89 fib(10) = 55 fib( 9) = 34 fib( 8) = 21 fib( 7) = 13 fib( 6) = 8 fib( 5) = 5 fib( 4) = 3 fib( 3) = 2 fib( 2) = 1 fib( 1) = 1 fib( 0) = 0 >>> Time: 0.000 seconds ------------- Iteration ------------- fib( 0) = 0 fib( 1) = 1 fib( 2) = 1 fib( 3) = 2 fib( 4) = 3 fib( 5) = 5 fib( 6) = 8 fib( 7) = 13 fib( 8) = 21 fib( 9) = 34 fib(10) = 55 fib(11) = 89 fib(12) = 144 fib(13) = 233 fib(14) = 377 fib(15) = 610 fib(16) = 987 fib(17) = 1597 fib(18) = 2584 fib(19) = 4181 fib(20) = 6765 fib(21) = 10946 fib(22) = 17711 fib(23) = 28657 fib(24) = 46368 fib(25) = 75025 fib(26) = 121393 fib(27) = 196418 fib(28) = 317811 fib(29) = 514229 fib(30) = 832040 fib(31) = 1346269 fib(32) = 2178309 fib(33) = 3524578 fib(34) = 5702887 fib(35) = 9227465 >>> Time: 0.000 seconds ------------- Linear Recursion ------------- fib( 0) = 0 fib( 1) = 1 fib( 2) = 1 fib( 3) = 2 fib( 4) = 3 fib( 5) = 5 fib( 6) = 8 fib( 7) = 13 fib( 8) = 21 fib( 9) =以上是关于LLVM 的DSA与APA优化的主要内容,如果未能解决你的问题,请参考以下文章