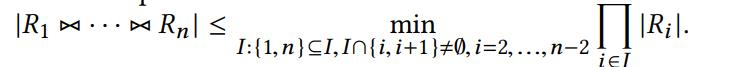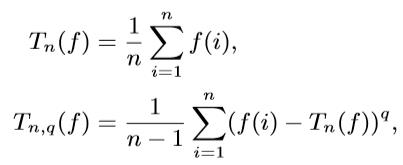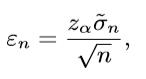在介绍本论文实现方法之前,我想先介绍下前人对join sample的工作,分别是Olken et al.和Chaudhuri et al [sigmod 99]在两表之间的join;和Acharya et al.[sigmod 99]基于外键的多表join;
-
Olken和Chaudhuri et al的工作(2-table joins)
首先是Olken的工作,他的策略如下:
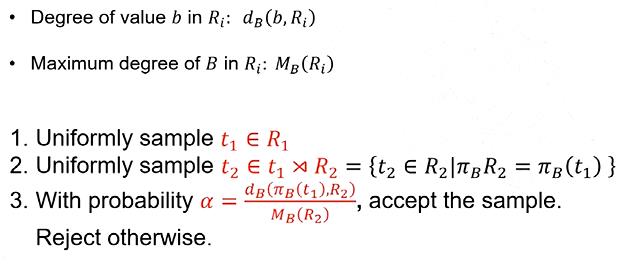
如果要对R1和R2做自然连接,需要先对R1做均匀采样,再对与R1选中的那个元组在R2中连接的那些元组做均匀采样,再以一个概率α接受这个采样;
我们举个例子来说明这样为什么是可行的。
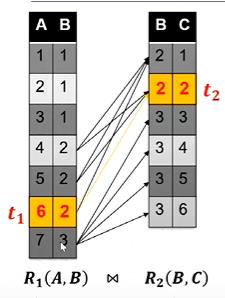
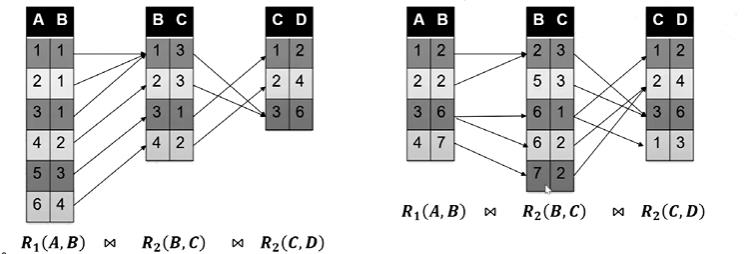
如上图所示,我们对R1和R2做自然连接操作,肉眼可以看出结果是10个元组,下面我们证明用以上方法进行随机抽样,接受一个样本的条件下,抽到正确的结果的概率是1/10;
首先计算选择到t1和t2并且被接受的概率;在R1上做均匀采样,那么我抽到t1的概率就是1/7,通过索引,我们可以快速找到t1对应的t2的元组有两个,则均匀在R2上抽取,获得t2的概率就是1/2了。最后我们以概率α拒绝这个采样,首先分子的计算方法就是t2的B属性的值在R2表上投影的个数,结果为2;分母就是对R2的B属性进行分组操作(Group by),取分组后个数的最大值,显然是B=3时候的分组,为4;所以α就是2/4为1/2;
随后我们计算一组结果被接受的概率;首先若在R1中抽到B的值为1时,概率为3/7,而α为0(因为R2中没有对应的结果元组);同理选中2并且接受的概率是3/7*2/4;选中3并且被接受的概率是1/7+4/4;所以加起来就是接受的概率,为10/28;
最后利用条件概率公式,如图所示,我们计算在接受的条件下,抽到t1t2的概率是1/10;由此验证了正确性;
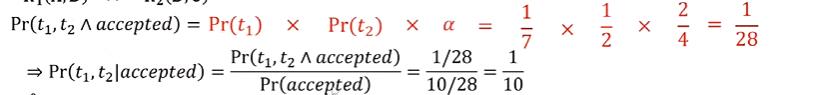
然后是和Chaudhuri et al的工作。他的步骤和操作更简单,不需要进行拒绝抽样样本,节省了时间,直接通过每个R1中元组的比例和的概率进行R1的采样,在R2中采样的方式和之前一样;
我们同样用例子说明结果的正确性;

还是以上图为例子,R1中B=1占在R2的比例是0;B=2在R2的比例是2+2+2=6;B=3在R2中占的比例是4;一共比例就是10;那么抽到t1的概率是用R2中B=2的个数除以10,就是2/10;抽到t2的概率就是1/2,这个元组是一定接收的;因此抽样的概率就是2/10*1/2是1/10;符合我们的要求。
-
Acharya et al.的工作(有外键条件下的连接)
他定义了一种特殊的连接条件的操作,就是如果一组连接中任意两个关系,他们的公共属性一定是靠前那个关系的外键,同时参考于后一个关系的主键;同时除了最后一个关系,前面的关系一定会找到一个关系和它配对,同时满足前面的条件。
如下图所示,左边的就是muliti-way foreign-key joins,右边则不是。
模型分为抽样部分和权重的上界估计部分,其中抽样模型是统一的,即根据权重进行随机抽样;权重上界估计模型的方法有许多,权重越精确,抽样时接受率越高,速度越快;权重不精确则计算权重时候更快;换句话说,精确权重的代价是计算权重的时间长;不精确的权重的代价是抽样时的拒绝率增加,速度缓慢;如何设计这两部分,是算法的关键。
-
抽样模型
可以看出,上面两种连接方案,一个是只能进行两表的连接;另一个则是对多表连接中的一种特殊情况进行讨论;而本作者对上面的论文进行了研究,提出了自己的一种普适性的多表连接方案。
首先对一个链式的多表连接,我们引出权重的概念,这个权重的意义就是用来表示一个连接操作的规模大小的,即一个元组的权重是这个元组和后续所有表做自然连接得到的结果数总和,即
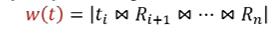
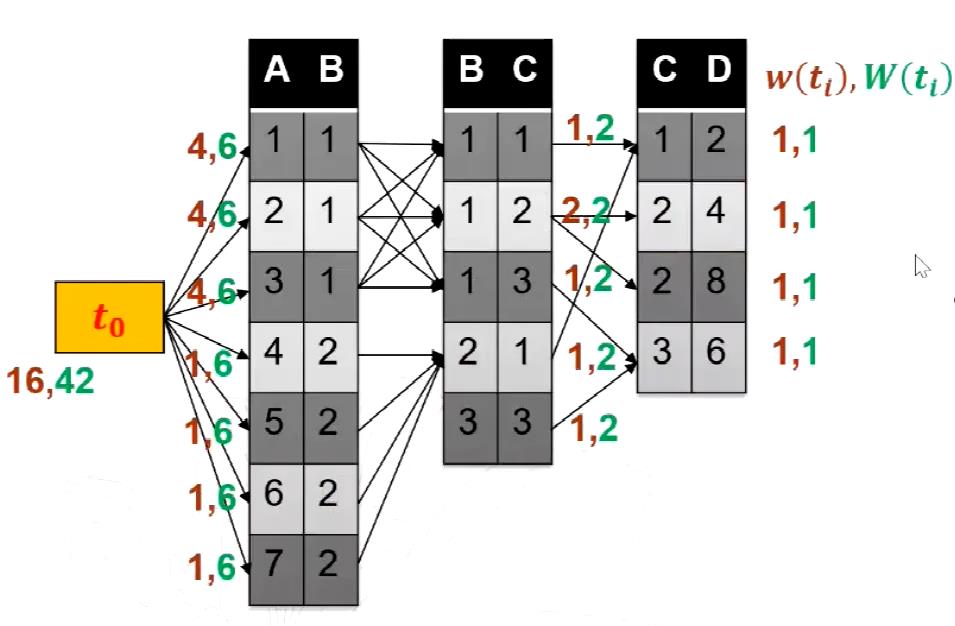
而一个表的权重,则是这个表上所有元组的权重之和。同时我们在最开头的表之前加一个头,用来记录第一个表R的W(R),一个例子如图所示,可以看出t0的权重其实就是连接结果的总个数。
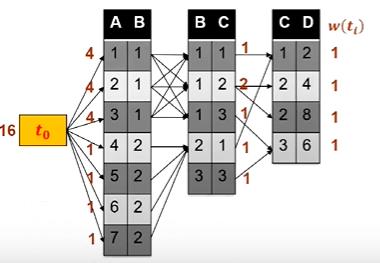
但是对于自然连接的抽样,想得出每个元组精确的权重的代价是很高的,我们希望得出一个对于连接规模上界的估计,即得出W的上界,这样的话时间开销就很小了,同时需要以一个概率拒绝这个采样,这样来保持抽样的正确性。
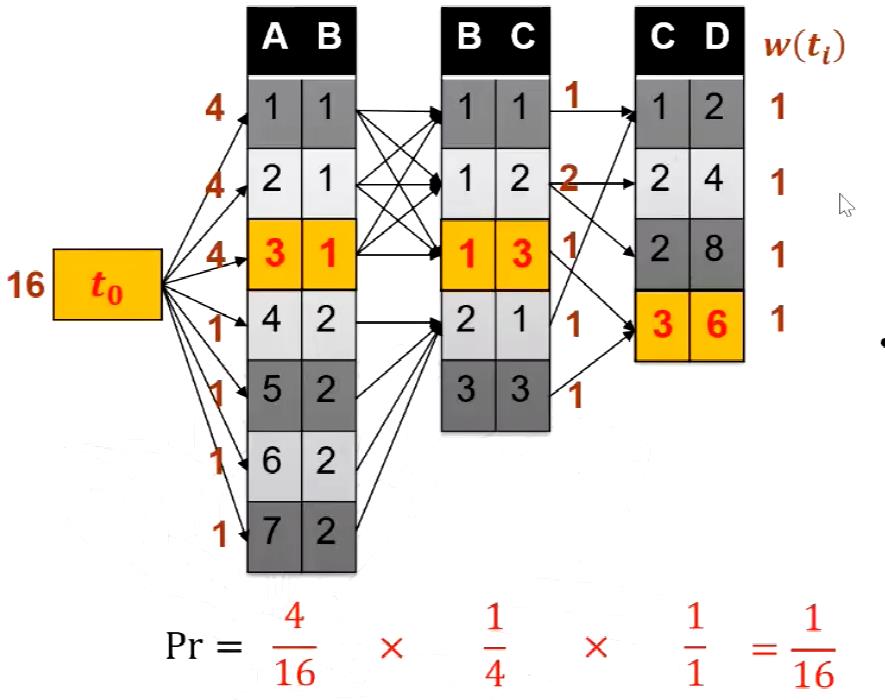
论文中提到的,我们拒绝这个采样的概率是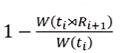 ,我们来证明这个拒绝率的正确性(假设w(t0)=|J|,即连接的结果总数为|J|),逻辑和思路和上面Olken的思路类似,如下图所示:
,我们来证明这个拒绝率的正确性(假设w(t0)=|J|,即连接的结果总数为|J|),逻辑和思路和上面Olken的思路类似,如下图所示:

具体的算法流程如图所示:

同样的为了方便理解,我们用一个例子来说明抽样的过程是怎么样的:
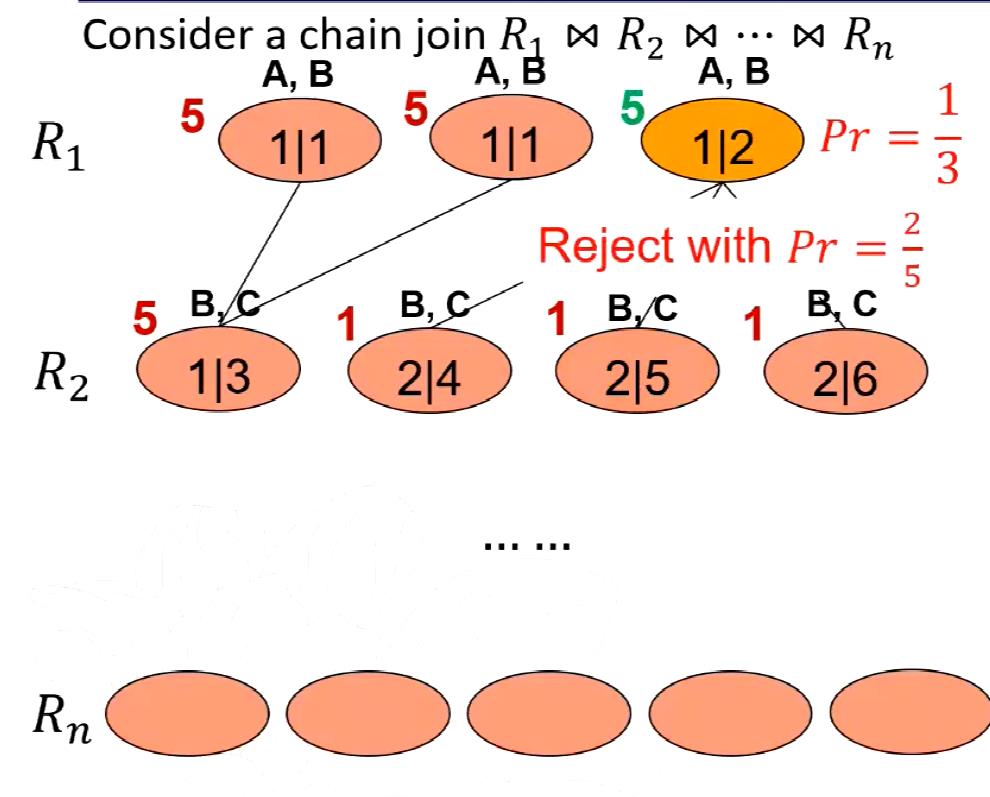
如上图所示,每个元组的权重上界标记在图中了,如果我们在R1中进行抽样,抽到第三个元组的概率就是5/(5+5+5)是1/3;拒绝率就是1-[(1+1+1)/5]就是2/5;
-
估计权重上界的方法
我们上面提到了每个元组的拒绝率的概念,若|J|是这条元组和后续关系做自然连接的结果数总和,那么对于每个元组的拒绝率就是 ,我们需要让这个上界尽可能的接近|J|,以达到拒绝率尽量小,一直接受的情况(这样效率最高)。
,我们需要让这个上界尽可能的接近|J|,以达到拒绝率尽量小,一直接受的情况(这样效率最高)。
那么下面就是对W上界的计算。作者对Olken、Chaudhuri和Acharya的方法进行了泛化,此后又提出了另一种基于random walk的方法对W的值进行估计和计算。值得注意的是,提出的四种方法中仅仅是计算W的方法不一样,进行抽样均使用上面提到的方法。下面对这四种方法进行阐述:
-
Exact Weight方法
这种方法是对Chaudhuri的方法进行了推广和泛化,把该方法从两个关系推广到多个关系。该方法被命名为Exact Weight(EW)方法。其实主要思想就是动态规划的思想,对每一个关系中的每一个元组精确计算其值。对于join关系中的最后一个表,将其初始化为1。再从后向前计算每一个表中的结果,对于满足连接条件的元组,将这些元组进行累加,就是前一个表中对应元组的权重的精确值。
这样Chaudhuri的方法就进行了拓展,从两个表泛化到多个表中。
这种方法的好处就是,结果是非常准确的,但是时间效率可能不高,它需要反复扫描各表中符合连接条件的元组进行赋值。
-
Reverse Sampling方法
这种方法是对Acharya的方法进行了移植,简称RS方法,这就直接是一种特殊情况,因为每个元组的权重都一定是1,直接1to1的采样就行了。
-
Extended Olken方法
这种方法对Olken中的方法进行了泛化和改进。论文中将其命名为Extended Olken (EO)方法。作者定义了一个频率的概念,即这个表种度最大的元组的权重就是这个表中所有元组的权重,即 。举个例子如下图所示:
。举个例子如下图所示:
绿色是估计的权重,红色是准确的权重,这样算权重肯定是大于准确值的,是准确权重的一个上界,同时我们只需要从上到下扫描一遍这个表找到度最大的元组,将这个元组的权重作为所有元组的权重就行了,效率是高于EW算法的。
可以看出,如果只用olken_bound估计的话,和真实值的代价差距很大,代价就是,我们总是会被拒绝!
所以,作者还引入了AGM Bound。在chain join的情况下,作者给出了AGM Bound的简化形式如下:
这两种方法在不同的情况下的优劣程度也不一样。如果某个表的最大频率很小,那么Olken的方法得到的上界可能更小一些。而当表的最大频率很大时(比如接近表本身的大小),Olken方法得到的上界可能很大。因此此时选用AGM Bound可以使得整体的上界更小。基于这样的观察,作者提出整合两种方法的混合方法。
该混合方法通过一个阈值h统计每个表R上频率大于h的元素和小于h的元素,并将该表分为RH(heavy部分)和RL(light部分)两部分,并在计算中对这两部分使用不同的方法进行计算,得到整体较低的上界。对于RH倾向于使用AGM方法,对于RL部分倾向于使用Olken方法。
-
Online Exploration方法
这种方法被命名为Online Exploration(OE)方法。该方法在该join关系上进行大量基于自然连接的随机游走(在每一个参与连接的表上,在下一个表中可以与当前元组进行连接的元组中均匀随机的选取一个),得到大量随机游走的结果序列,并在这个过程中保存得到每一个序列的概率。
此后对于每一个表上的每一个元组,设置一个阈值。其中在random walk中到达该元组达到该阈值次数的,使用wander join estimator对上界进行估计。对于未到达该阈值的,使用Exact Weight中的动态规划方法进行计算。
对于random walk,我们随机选择一条通路,从后往前通过选中这条通路的概率,来计算当前通路上各个元组的权值。
同样的,用一个例子说明随机游走的算法是怎么样的,如下图所示的三个关系的链式连接操作:
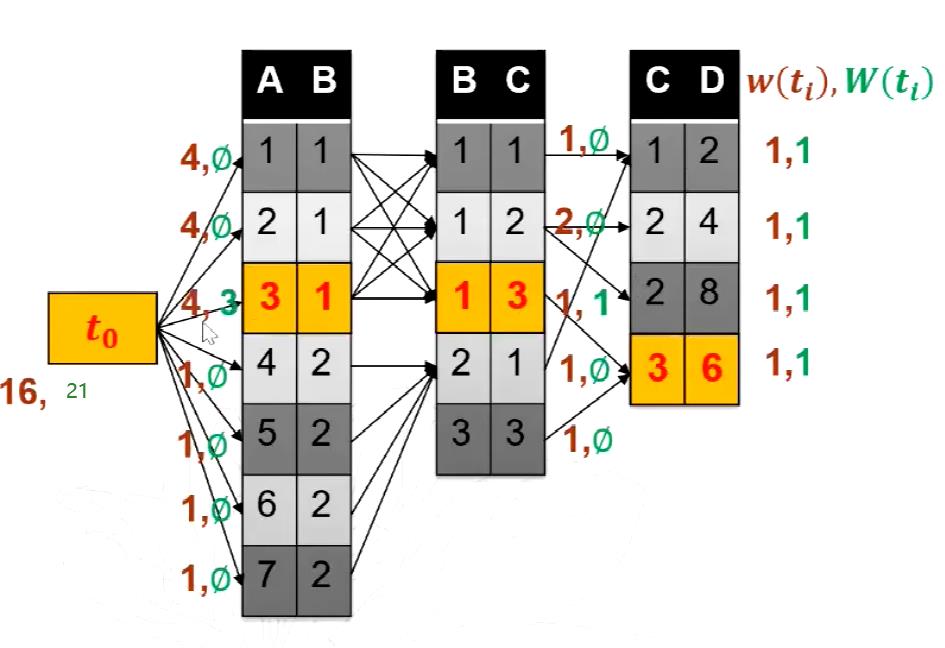
首先最后一个表的元组权重全部赋值为1,其它表的初始权值设置为空(或为0),对于我随机选中的这条通路,从后往前运动,先看R2表中对应的元组,这个元组是唯一指向R3的,所以权重更新为1;再看R1中的元组这个元组以1/3的概率指向R2选中的元组,因此它的权重更新为1除以1/3,更新为3;再看t0的权重,它是以1/7的概率指向通路的那条元组的,因此它的权重更新为3除以1/7,更新为21;
实际上我们得到估计值的期望后,需要给予一定的置信度,利用上(α+1)/2-分位数计算置信区间。此后,使用期望+置信区间/2作为最终的W估计值。对于具体的计算公式,由于W函数应为数据库函数中的COUNT函数。给定如下的函数定义:
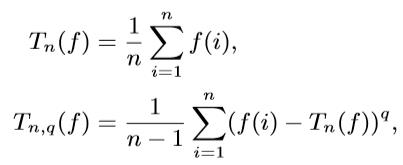
由以上公式得到期望和方差的值后,我们给定置信区间α,使用如下公式计算置信区间的大小:
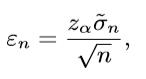
其中zα是均值为0,方差为1的正态分布函数的(α+1)/2-分位数。
-
除了链式连接的其它连接形态
通过以上的两个抽样模型和计算权重模型,我们已经可以求出任意的链式连接的抽样结果了,而对于更多复杂的情况,我们还有树形连接、有环连接和带有选择的连接,如下图所示。
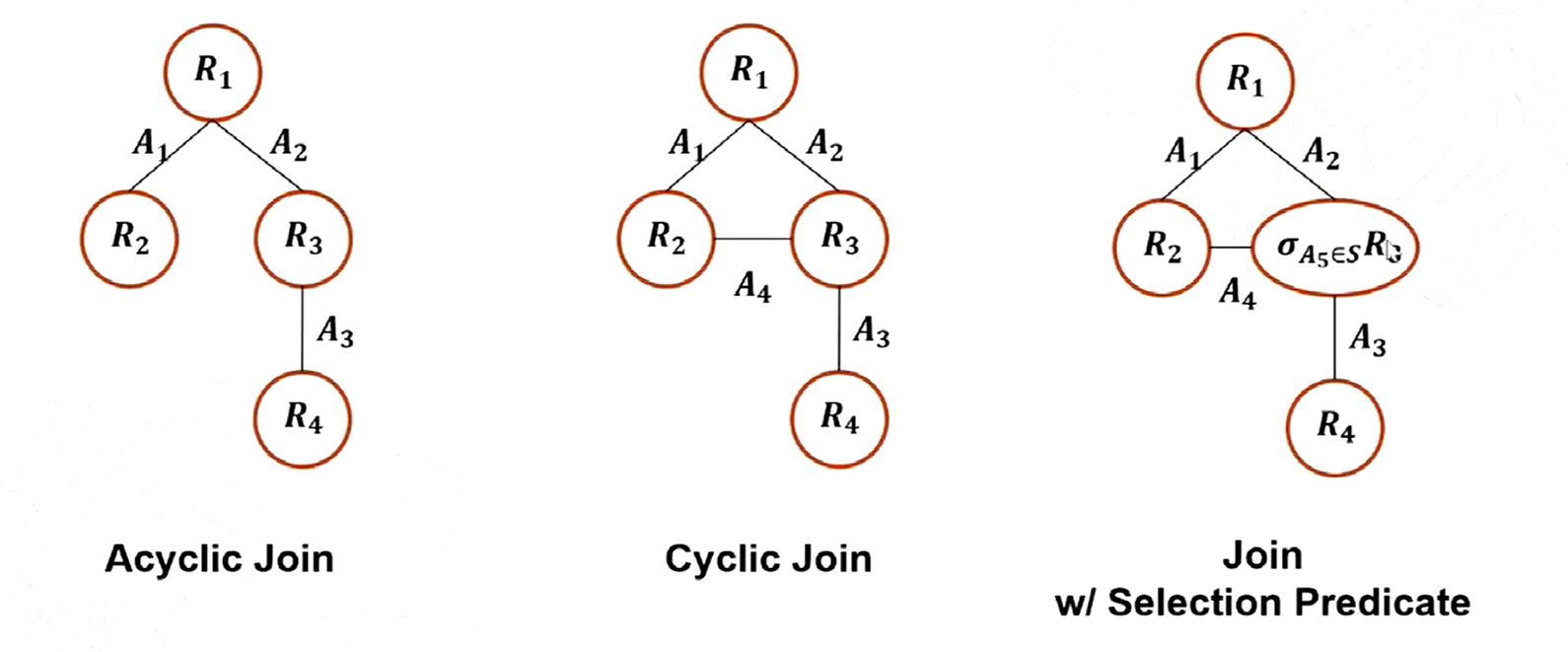
-
Acyclic Join
对于树形的连接,对于权重计算模型,我们修正计算方法为:一个结点的权重等于他所有孩子结点的上界的乘积,这是因为孩子结点的计算都是互相独立的,所有孩子结点计算过程中并不依赖其它结点。
而抽样模型则是采用递归的方式进行抽样,对于根节点的抽样结果,我们要先对所有孩子结点进行抽样,然后将抽样结果进行合并即可,这就是一个递归的程序过程,而拒绝率我们则修正为以下情况。

-
Cyclic Join
而对于一个循环连接的情况,我们可以把任意一个带有循环的连接,拆为链式的和树形的连接,如图所示,我们可以将以下连接的R3或者R5拿出来变成链式和树形的连接。
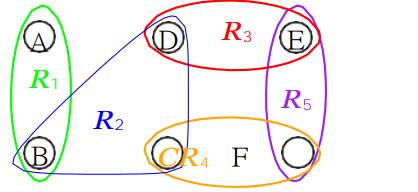
特殊的,我们要对每个循环进行验证,就是我们虽然将他们拆分成两个连接,但是对于公共的属性,我们要保证两个连接的属性对应的值相同,如果不相同,我们就拒绝这个采样。
-
带有选择的Join
对于有选择的情况非常简单,我们只需要先对表加一个选择过滤器就行了,可以采用必要的选择下推技术,让表尽早的变小,这样反而能加速连接的速度。
-
作者实验的结果分析
-
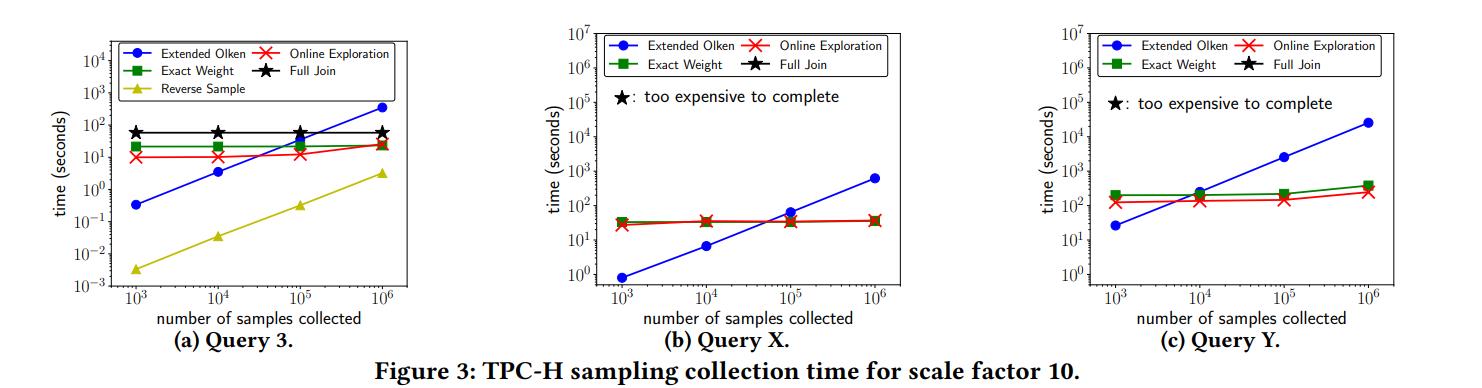
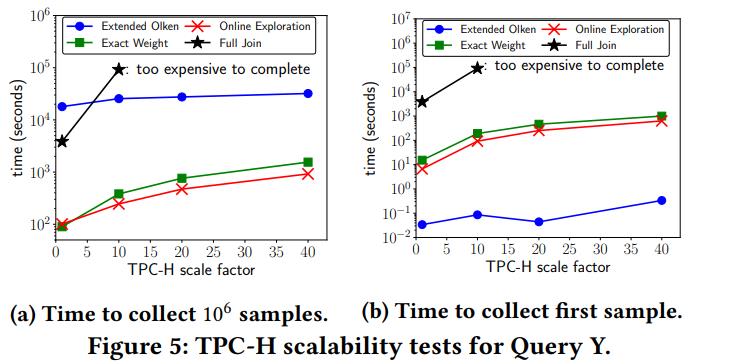
抽样时间对比
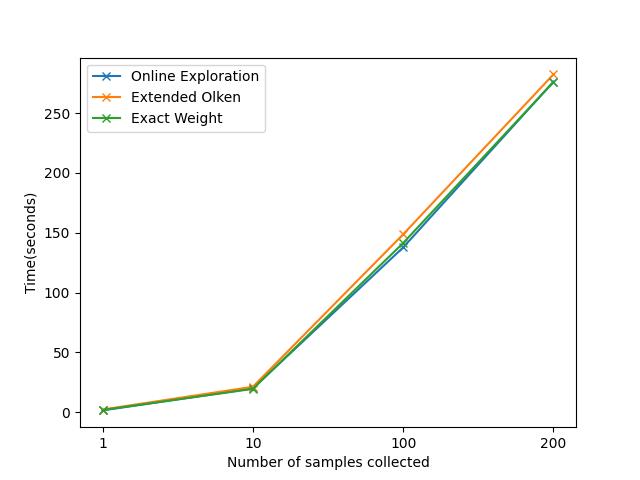
在TCP-H和推特关系两个数据集进行连接测试,对于特定的采样RS算法是最快的;对于EO它在抽样数比较小的时候,采样时间很短,但是随着抽样数的增加,它在后面拒绝的概率越来越高,时间就会快速增加;而EW和OE算法,则由于上界估计的比较准确,抽样时间保持稳定的提示(注意,虽然图里面看起来抽样个数随着时间的变化情况是平的,变化不明显;但是这是因为纵坐标是不是均匀的,是一个取对数才均匀变化的的坐标轴)
-
大致设计思路
由于计算资源和时间的限制,我们在相对原论文中的数据集较小的数据集上进行试验。我们在相同的query上采样不同规模的的sample,并记录其运行时间,同时我们用EO,EW,OE三种方法来估计权重,因为RS方法需要连接条件是外键的情况。我们来通过实验比较这三种方法的时间效率。除此之外,我们比较三种方法在输出第一个采样结果时间的比较,以分析三种方法计算W值的效率。
根据原论文中的设置,我们设定如下查询的query:
-
Query1: popular user, twitter user的2-join query。
-
Query2: twitter user,popular user, twitter user的3表循环链式join query。
-
Query3: popular user, twitter user,popular user, twitter user,popular user的五表循环链式连接
-
实验的必要性分析
-
对于两表连接
对于Query1仅仅进行两表的连接,使用如下sql语句:
结果如下图所示:
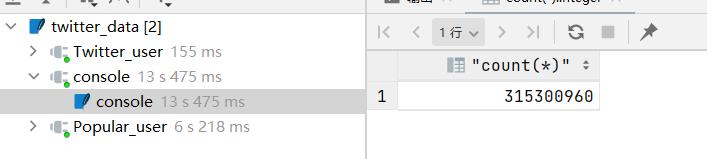
如图所示,结果就已经达到3亿级别了,这种级别的数据,很难全部放入后续的训练集中进行训练,需要抽样才行。
-
对于少量多表连接
对于Query2,使用如下sql语句进行自然连接,结果如图所示,运行了1小时还没算出来,已经不可能先算出来全部结果再抽样了。
-
对于大量多表连接
对于Query3,更不必说,结果呈指数级别上升,普通的fulljoin已经不可能计算出全部的结果了。甚至权重估计也变的缓慢,需要策略进行优化。
-
代码部分的编写
整体设计思路是,针对论文提出的三种主要的估计权重上界的方法(省去了RS方法,因为RS方法比较简单(只需要1 to 1 map),而且需要特定的数据集(外键连接的情况),就没进行实验),在1,10,100,200的sample num上进行实验,分别计算产生sample需要的时间和从开始到产生第一个sample需要准备的时间。
-
EW方法
就说从最后一个表向前面扫描,最后一个表中元组的权重都是1,前面的表利用数据库的倒叙查找操作进行动态规划赋值即可。
关键代码如图所示:
-
EO方法
首先是对于EO方法,Olken bound需要获得当前表的最大频率主键的频率。在原论文中,作者提出在数据库大规模查询的过程中,最大主键频率一般是会被统计和保存的。
然而在本次实验中,是直接将数据集中的数据加载到数据库中做各种操作,因此不可能获得这样的统计数据,因此,我们显式统计所有元组的频率,然后记录最大频率元组的频率。同时我在统计生成第一个sample准备时间时,剪掉了这个过程所需的时间。
对于EO方法,需要将AGM bound 和 Olken bound结合使用。该思路的思想是当表的最大频率较大时(例如接近表的频率),Olken bound可能会过大,此时适合使用AGM bound。否则适合使用Olken bound。因此将每一个表利用一个阈值频率,将其分为Heavy和Light部分。我们将除第一个表外所有的表区分为Heavy和Light部分,并分别给出AGM bound和Olken bound下的结果,取其中较小的结果,最后相加。实验中我们设置阈值为400进行heavy和light的区分。基于现有计算能力,我们分别抽取1,10,100,200个sample进行实验。
关键代码如下图所示:
-
OE方法
首先我们进行random walk,记录每个元组被游走的次数;随后对于游走次数大于一定值的元组,我们认为它是关键结点,这时候对这个元组使用wanderJoin进行估计,否则使用动态规划进行估计,对于Online Exploration方法,我们设置random walk次数为2000000次,其中经过次数大于200次的利用estimator进行估计,小于200次的使用动态规划进行估计。
关键代码如图所示。
-
实验环境
-
运行环境
CPU: Intel(R) Core(TM) i7-8565U CPU @ 1.80GHz 1.99 GHz
RAM: 8GB
OS: Windows 10 64bit
-
程序环境
编译环境:Python 3.8
IDE:Pycharm
数据库:Sqlite3数据库引擎
-
数据
我的笔记本无法对原论文中提供的数据集进行试验。正如论文所说,经过统计,发现整个数据集共有36G,超过19亿条数据。且原论文中使用的popular user关系并未直接提供,需要进行预处理(绘制粉丝关系图,找到popular user)。而这个过程对于我现有的计算资源很难完成。因此,我选择了相对适合当前实验的数据集予以替代。
我找到了斯坦福SNAP提供的推特用户关系数据集。该数据集的数据规模在百万级别,大小约为100MB.我们使用SNAP for python工具建立该数据集的关系图,并从中提取入度超过一定阈值的节点作为popular user,提取与这些节点有关的记录组成popular user表,用做实验的join query。
经过斯坦福提供的SNAP工具处理后,我们的twitter user人数为2420766个,popular user的人数为937159个;尽管如此,仅仅twitter user和popular user做连接操作,结果数就达到了315300960个,可以进行算法的验证实验。
-
实验结果
利用以上设置,对于我们设置的Query,我们有如下运行时间结果:
-
Query1 2-join sample产生的速度数据和图表:
time=[[1.40625, 19.796875, 137.703125, 276.265625], [2.140625, 21.171875, 148.65625, 282.421875], [1.75, 19.40625, 141.375, 276.046875]]
-
Query2 3循环join sample产生的速度数据和图表:
time=[[5.609375, 58.9375, 481.328125, 937.46875], [3.5625, 90.5625, 731.90625, 1655.0625], [2.734375, 50.84375, 396.15625, 786.53125]]
-
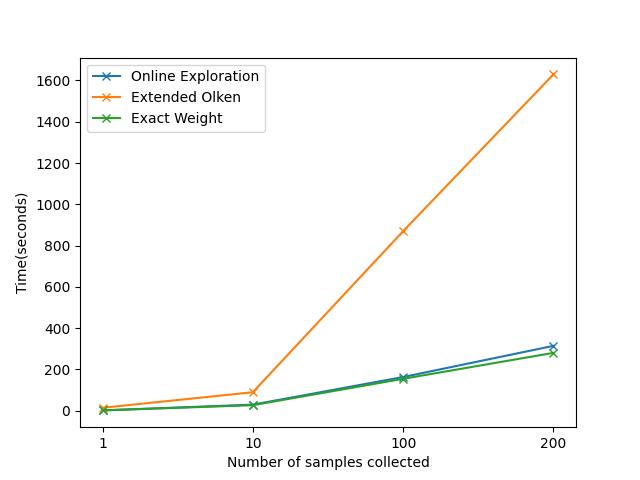
Query3 5循环join sample产生的速度数据和图表
time=[[1.984375, 29.75, 163.53125, 314.453125], [14.609375, 89.859375, 869.984375, 1629.109375], [1.890625, 27.140625, 154.9375, 280.53125]]
-
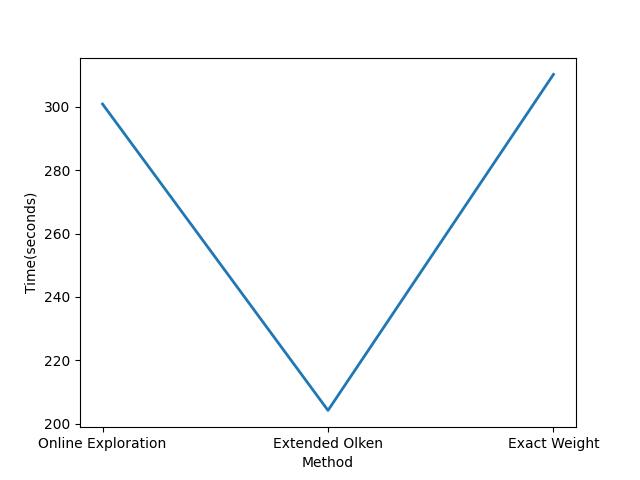
三种算法准备时间对比
我们通过多次运行sample,同时对不同方法准备时间做了些优化(数据量过少,分布过于密集,frequency的维护问题),得出不同的方法在query中获得第一个sample所需时间来比较三种方法进行sample的准备所需的时间。统计结果如下:
-
实验结果及分析
-
Sample分析
限于计算资源和时间,我们选用的抽取数量与原文中不完全相同。但根据论文中的实验结果和复现后的实验结果,运行时间的走势有一定相似:
- 首先由于OE方法和EW方法都会在某种情况下使用动态规划算法,只是OE算法对EW算法中关键结点进行了优化(使用随机游走)则其W值相似度可能较高,且是比较准确的,因此抽样时候的通过率比较高,因此OE和EW在产生sample时间方面是近似且时间短的。
- 对于EO方法,可以看到在3个表以上的情况下其时间复杂度随sample数增加很快。这是因为,抽取样本数较少时,该方法计算得到的bound不如EW精确,仍可以以相对较快的速度进行sample。然而当sample数量迅速增加时,由于W上界计算的不精确性导致sample的拒绝率较高,因此sample所需时间迅速上升。
- 两个表直接连接时,三种方法的时间大致相同,这是因为几乎不会拒绝,权重不会影响到采样的效率。
-
准备时间分析
对于产生第一个sample所需时间的统计结果可以印证上述的推断。根据统计结果,三种方法所需的准备时间EO是最少的,OE方法次之,EW方法最高。
- 由于EO方法在计算W值的过程中不需要额外的准备时间只需要通过最高的frequency进行赋值即可,因此时间最短。
- 对于OE方法,具体的准备时间与random walk次数有关系。OE在random walk过程中需要进行下一个结点的选择和概率的记录,在所有random walk结束后才开始计算W值,因此所花时间较长。而对于遍历次数比较多的元组,能迅速用wanderjoin估计权重,其余的才用EW估计。
- EW对每一个节点使用动态规划精确计算W值,因此所需时间最长。
-
反思
可以看到,尽管在相同的sample数量下实验取得和原论文中相同量级的结果,但实际上复现模型效果仍与原论文中的结果有很大差距。主要是OE算法的随机游走时间好像过于缓慢;同时EW算法又有点偏快了,这一点比较让人困扰。
- 首先是因为复现选用的数据集相比原论文中使用的数据集小了很多,EO算法和EW算法在准备时间上,没有像论文那样拉开差距,如果数据量达到他的19亿级别,EO算法在有frequency直接维护的前提下,速度应该很快,直接赋值权重就可以进行权重上界的估计。
- 本次复现中同时使用Sqlite3数据库引擎进行索引操作和用python进行查找操作,数据库层面进行查找肯定是更快的,但是进行随机游走的时候,不得不用python手动实现,这就导致了横向对比上,OE算法好像慢了许多;而EW算法完全用数据库索引查找,然后赋值,速度上快了一些。
- 论文中有大量未交代清楚的实现细节,因此复现结果可能有所差距。而且模型在不同的处理器上运行,并行运算方面我们也没有考虑,因此算力不同导致实验结果相对较差。
 的结果U,我们希望获得一组随机抽样结果S,使得抽样结果S中的每个元素e均匀独立等可能的出现在结果U中。
的结果U,我们希望获得一组随机抽样结果S,使得抽样结果S中的每个元素e均匀独立等可能的出现在结果U中。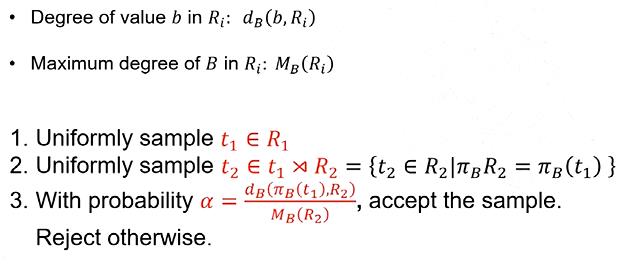

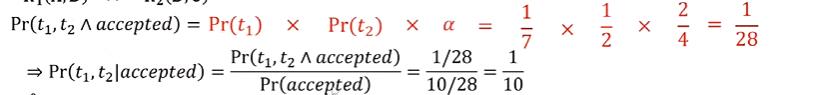

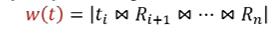

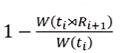 ,我们来证明这个拒绝率的正确性(假设w(t0)=|J|,即连接的结果总数为|J|),逻辑和思路和上面Olken的思路类似,如下图所示:
,我们来证明这个拒绝率的正确性(假设w(t0)=|J|,即连接的结果总数为|J|),逻辑和思路和上面Olken的思路类似,如下图所示:


 ,我们需要让这个上界尽可能的接近|J|,以达到拒绝率尽量小,一直接受的情况(这样效率最高)。
,我们需要让这个上界尽可能的接近|J|,以达到拒绝率尽量小,一直接受的情况(这样效率最高)。
 。举个例子如下图所示:
。举个例子如下图所示: