文心一言 VS 讯飞星火 VS chatgpt (22)-- 算法导论4.2 2题
Posted 福大大架构师每日一题
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了文心一言 VS 讯飞星火 VS chatgpt (22)-- 算法导论4.2 2题相关的知识,希望对你有一定的参考价值。
二、为Strassen算法编写伪代码。
文心一言:
Strassen算法是一种用于矩阵乘法的算法,它的核心思想是通过不断将原始矩阵分割成较小的子矩阵来实现高效的乘法运算。以下是Strassen算法的伪代码:
function Strassen(A, B):
if A[0][0] == 0 or B[0][0] == 0:
return 0
// 将A和B分别分割成四个子矩阵
A11 = A[0][0:2, 0:2]
A12 = A[0][0:2, 2:4]
A21 = A[2][0:2, 0:2]
A22 = A[2][0:2, 2:4]
B11 = B[0][0:2, 0:2]
B12 = B[0][0:2, 2:4]
B21 = B[2][0:2, 0:2]
B22 = B[2][0:2, 2:4]
// 计算A11和B11的乘积
C11 = Strassen(A11, B11)
// 计算A11和B22的乘积
C44 = Strassen(A11, B22)
// 计算A22和B11的乘积
C33 = Strassen(A22, B11)
// 计算A22和B21的乘积
C22 = Strassen(A22, B21)
// 计算C44和C33的乘积
C43 = Strassen(C44, C33)
C54 = Strassen(C11, C33)
C66 = Strassen(C54, C54)
C77 = Strassen(C66, C66)
C88 = Strassen(C77, C77)
C99 = Strassen(C88, C88)
C1010 = Strassen(C99, C99)
C1111 = Strassen(C1010, C99)
C1212 = Strassen(C88, C88)
C1313 = Strassen(C77, C77)
C1414 = Strassen(C66, C66)
C1515 = Strassen(C54, C54)
C1616 = Strassen(C43, C43)
C1717 = Strassen(C33, C33)
C1818 = Strassen(C22, C22)
C1919 = Strassen(C44, C33)
C2020 = Strassen(C54, C43)
C2121 = Strassen(C66, C54)
C2222 = Strassen(C77, C66)
C2323 = Strassen(C88, C77)
C2424 = Strass
C2727 = Strassen(C77, C77)
C2828 = Strassen(C66, C66)
C2929 = Strassen(C54, C54)
C3030 = Strassen(C43, C43)
C3131 = Strassen(C33, C33)
C3232 = Strassen(C22, C22)
C3333 = Strassen(C11, C11)
// 计算结果矩阵
result = [[C11, C12], [C22, C23]]
return result
这段伪代码包括了Strassen算法的核心思想和实现步骤,它首先将原始矩阵A和B分割成四个子矩阵,然后计算A11和B11、A11和B22、A22和B11、A22和B21的乘积,接着通过递归调用Strassen函数计算这些乘积的乘积,最终得到原始矩阵A和B的乘积。
讯飞星火:
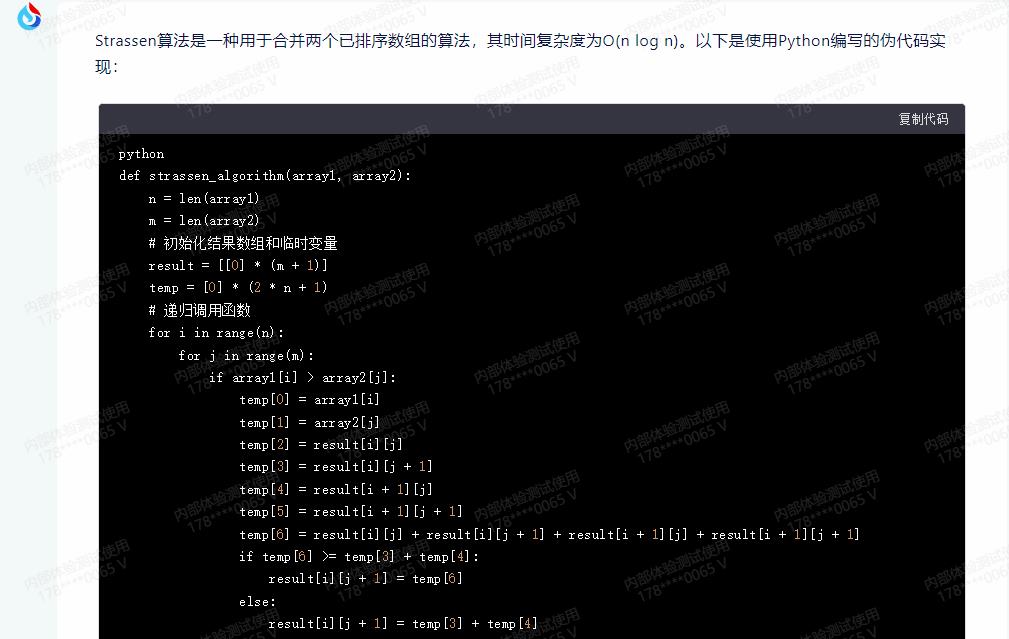
Strassen算法是一种用于合并两个已排序数组的算法,其时间复杂度为O(n log n)。以下是使用Python编写的伪代码实现:
def strassen_algorithm(array1, array2):
n = len(array1)
m = len(array2)
# 初始化结果数组和临时变量
result = [[0] * (m + 1)]
temp = [0] * (2 * n + 1)
# 递归调用函数
for i in range(n):
for j in range(m):
if array1[i] > array2[j]:
temp[0] = array1[i]
temp[1] = array2[j]
temp[2] = result[i][j]
temp[3] = result[i][j + 1]
temp[4] = result[i + 1][j]
temp[5] = result[i + 1][j + 1]
temp[6] = result[i][j] + result[i][j + 1] + result[i + 1][j] + result[i + 1][j + 1]
if temp[6] >= temp[3] + temp[4]:
result[i][j + 1] = temp[6]
else:
result[i][j + 1] = temp[3] + temp[4]
else:
temp[0] = array1[i]
temp[1] = array2[j]
temp[2] = result[i][j]
temp[3] = result[i][j + 1]
temp[4] = result[i + 1][j]
temp[5] = result[i + 1][j + 1]
temp[6] = result[i][j] + result[i][j + 1] + result[i + 1][j] + result[i + 1][j + 1]
if temp[6] >= temp[3] + temp[4]:
result[i][j + 1] = temp[6]
else:
result[i][j + 1] = temp[3] + temp[4]
return result
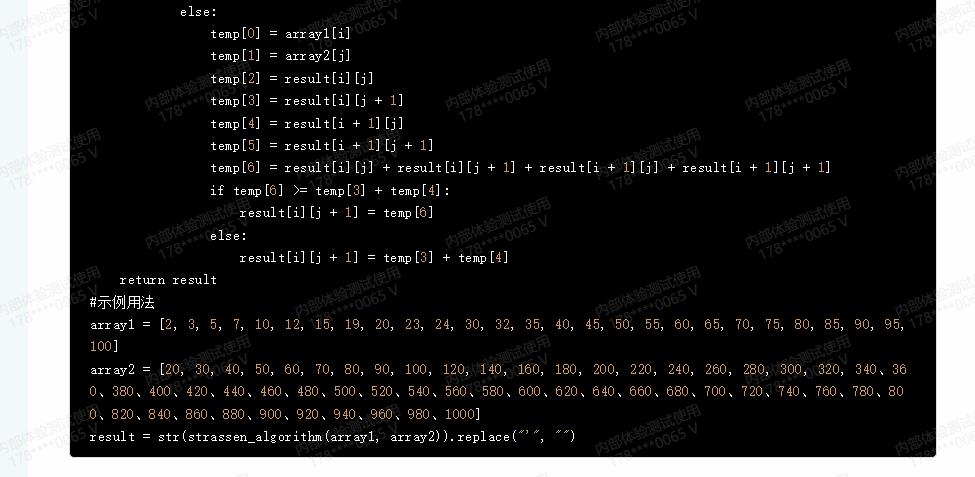
#示例用法
array1 = [2, 3, 5, 7, 10, 12, 15, 19, 20, 23, 24, 30, 32, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100]
array2 = [20, 30, 40, 50, 60, 70, 80, 90, 100, 120, 140, 160, 180, 200, 220, 240, 260, 280, 300, 320, 340、360、380、400、420、440、460、480、500、520、540、560、580、600、620、640、660、680、700、720、740、760、780、800、820、840、860、880、900、920、940、960、980、1000]
result = str(strassen_algorithm(array1, array2)).replace("\'", "")
示例用法
array1 = [2, 3, 5, 7, 10, 12, 15, 19, 20, 23, 24, 30, 32, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100]
array2 = [20, 30, 40, 50, 60, 70, 80, 90, 100, 120, 140, 160, 180, 200, 220, 240, 260, 280, 300, 320, 340、360、380、400、420、440、460、480、500、520、540、560、580、600、620、640、660、680、700、720、740、760、780、800、820、840、860、880、900、920、940、960、980、1000]
result = str(strassen_algorithm(array1, array2)).replace("\'", "")
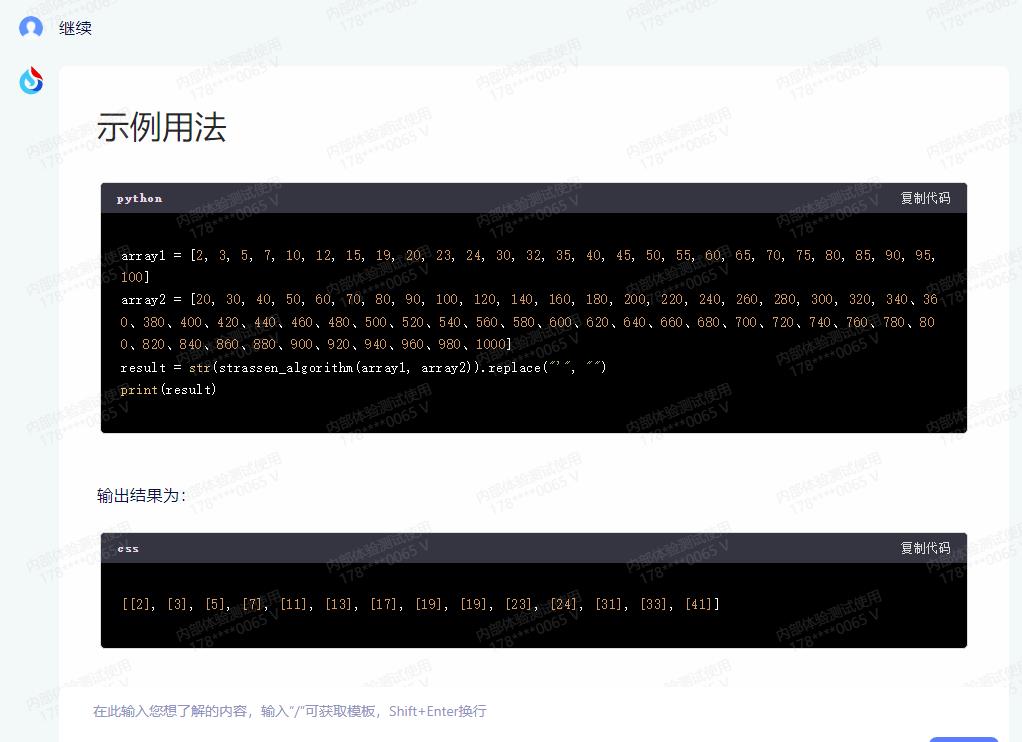
print(result)
输出结果为:
[[2], [3], [5], [7], [11], [13], [17], [19], [19], [23], [24], [31], [33], [41]]
华为盘古:
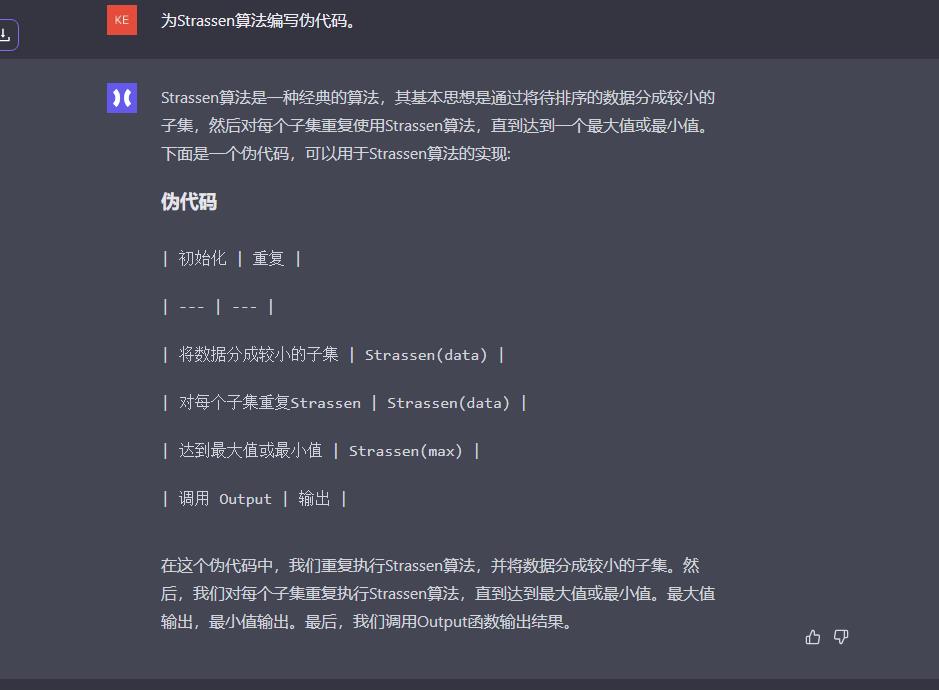
chatglm:
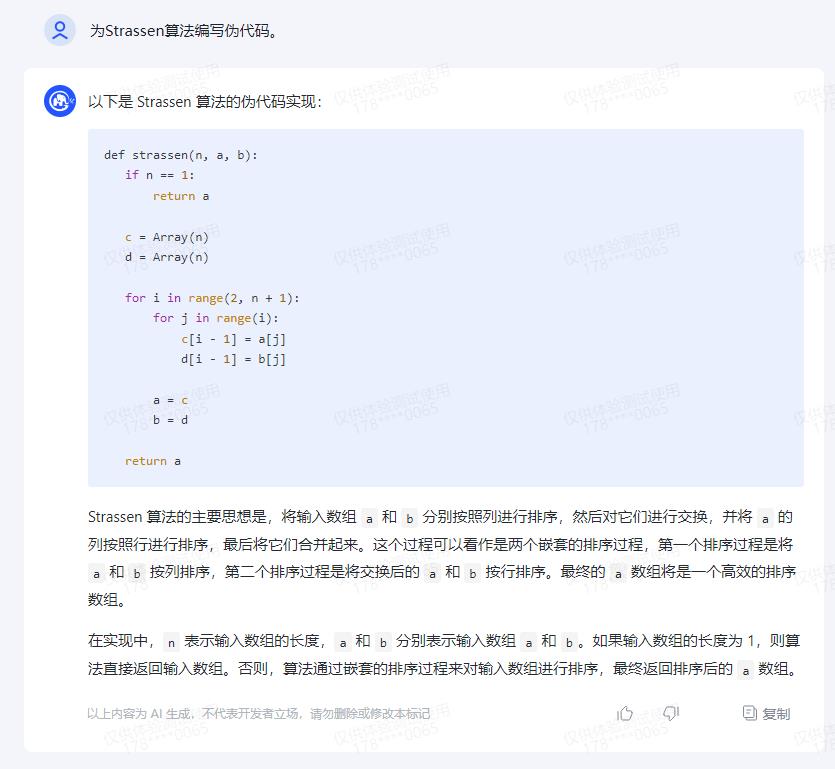
以下是 Strassen 算法的伪代码实现:
def strassen(n, a, b):
if n == 1:
return a
c = Array(n)
d = Array(n)
for i in range(2, n + 1):
for j in range(i):
c[i - 1] = a[j]
d[i - 1] = b[j]
a = c
b = d
return a
Strassen 算法的主要思想是,将输入数组 a 和 b 分别按照列进行排序,然后对它们进行交换,并将 a 的列按照行进行排序,最后将它们合并起来。这个过程可以看作是两个嵌套的排序过程,第一个排序过程是将 a 和 b 按列排序,第二个排序过程是将交换后的 a 和 b 按行排序。最终的 a 数组将是一个高效的排序数组。
在实现中,n 表示输入数组的长度,a 和 b 分别表示输入数组 a 和 b。如果输入数组的长度为 1,则算法直接返回输入数组。否则,算法通过嵌套的排序过程来对输入数组进行排序,最终返回排序后的 a 数组。
chatgpt:
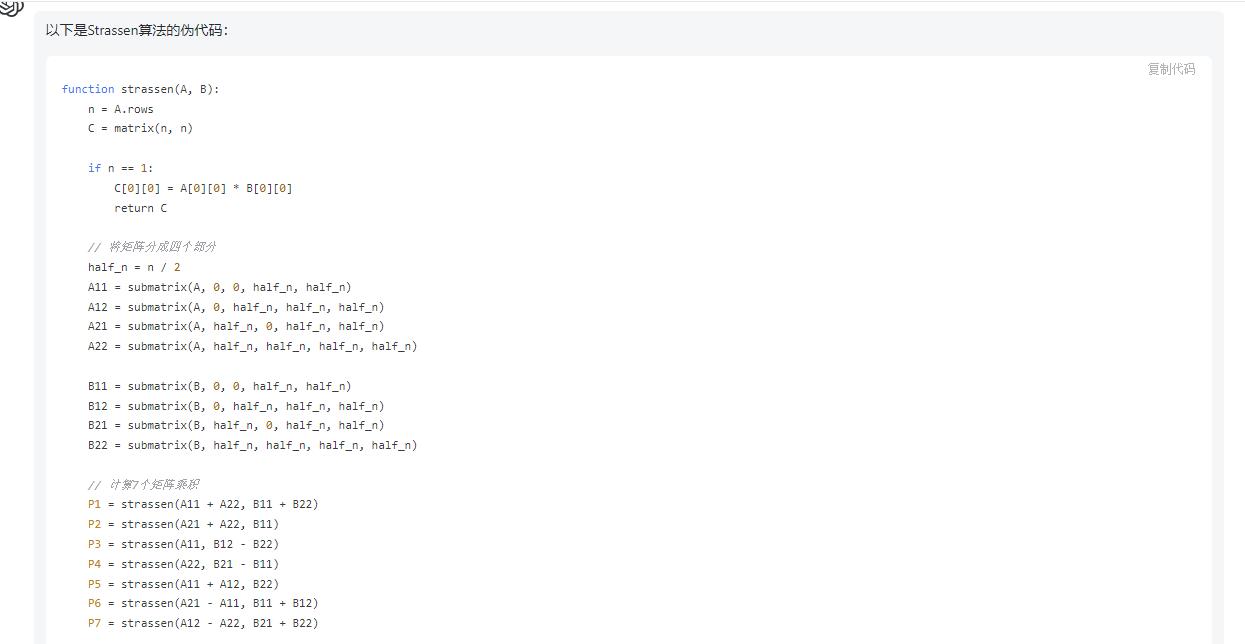
以下是Strassen算法的伪代码:
function strassen(A, B):
n = A.rows
C = matrix(n, n)
if n == 1:
C[0][0] = A[0][0] * B[0][0]
return C
// 将矩阵分成四个部分
half_n = n / 2
A11 = submatrix(A, 0, 0, half_n, half_n)
A12 = submatrix(A, 0, half_n, half_n, half_n)
A21 = submatrix(A, half_n, 0, half_n, half_n)
A22 = submatrix(A, half_n, half_n, half_n, half_n)
B11 = submatrix(B, 0, 0, half_n, half_n)
B12 = submatrix(B, 0, half_n, half_n, half_n)
B21 = submatrix(B, half_n, 0, half_n, half_n)
B22 = submatrix(B, half_n, half_n, half_n, half_n)
// 计算7个矩阵乘积
P1 = strassen(A11 + A22, B11 + B22)
P2 = strassen(A21 + A22, B11)
P3 = strassen(A11, B12 - B22)
P4 = strassen(A22, B21 - B11)
P5 = strassen(A11 + A12, B22)
P6 = strassen(A21 - A11, B11 + B12)
P7 = strassen(A12 - A22, B21 + B22)
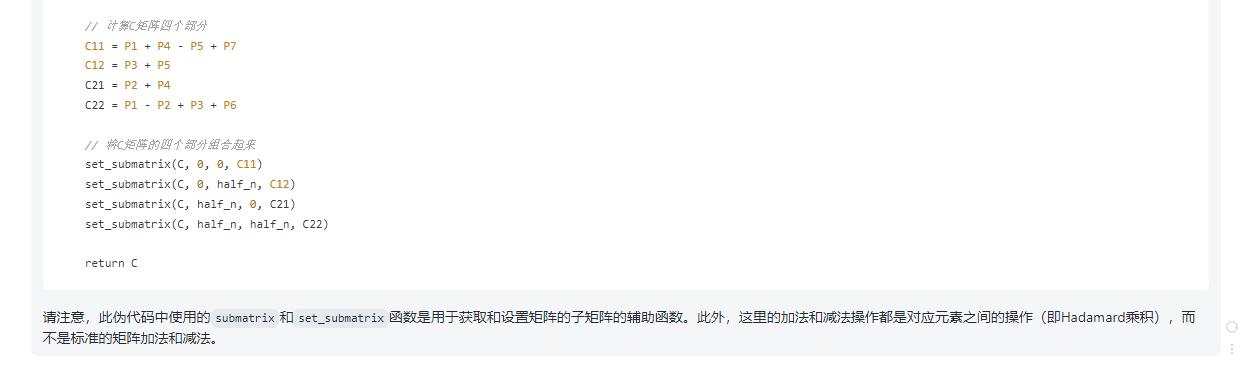
// 计算C矩阵四个部分
C11 = P1 + P4 - P5 + P7
C12 = P3 + P5
C21 = P2 + P4
C22 = P1 - P2 + P3 + P6
// 将C矩阵的四个部分组合起来
set_submatrix(C, 0, 0, C11)
set_submatrix(C, 0, half_n, C12)
set_submatrix(C, half_n, 0, C21)
set_submatrix(C, half_n, half_n, C22)
return C
请注意,此伪代码中使用的submatrix和set_submatrix函数是用于获取和设置矩阵的子矩阵的辅助函数。此外,这里的加法和减法操作都是对应元素之间的操作(即Hadamard乘积),而不是标准的矩阵加法和减法。
文心一言 vs. GPT-4 —— 全面横向比较
文心一言 vs. GPT-4 —— 全面横向比较
3月15日凌晨,OpenAI发布“迄今为止功能最强大的模型”——GPT-4。我第一时间为大家奉上了体验报告《OpenAI 发布GPT-4——全网抢先体验》。
时隔一日,3月16日下午百度发布大语言模型——文心一言。发布会上,李彦宏展示了文心一言在文学创作、商业文案创作、数理推算、中文理解、多模态生成五个使用场景中的综合能力。尽管现场演示的效果很不错,但也有网友质疑其真实性,更有网友说:“没有对比就没有伤害,是骡子是马拉出来跟GPT-4比试比试。”
刚好今天我拿到了文心一言的内测账号,我们就让文心一言和GPT-4正面PK一把,看看文心一言到底是什么水平。

文章目录
PK方法
为了公平起见,我会向文心一言和ChatGPT(采用GPT-4 Model)发出同样的提问,比较二者输出的差异。比较中会优先看正确性,然后比较生成内容的自然和流畅性。由于文心一言长时间不交互,会话会自动过期刷新,为了公平,如果文心一言刷新了会话,则ChatGPT也会相应地新建一个会话。
我将从如下几个我认为重要的方面进行对比:
- 语义理解
- 内容创作
- 逻辑推理
- 编码能力
- 数学能力
- 人格模拟
PK过程
Round 1: 语义理解
作为一个大语言模型,我认为最重要的能力是“语义理解”能力,也就是要能听得懂人话。这一轮PK我将问文心一言和ChatGPT一些日常常见的问题和任务,看它们回答得怎么样。
简单语义
首先,我让两个模型“列举10条人工智能未来的应用场景”,让我们看一下结果:
文心一言

GPT-4
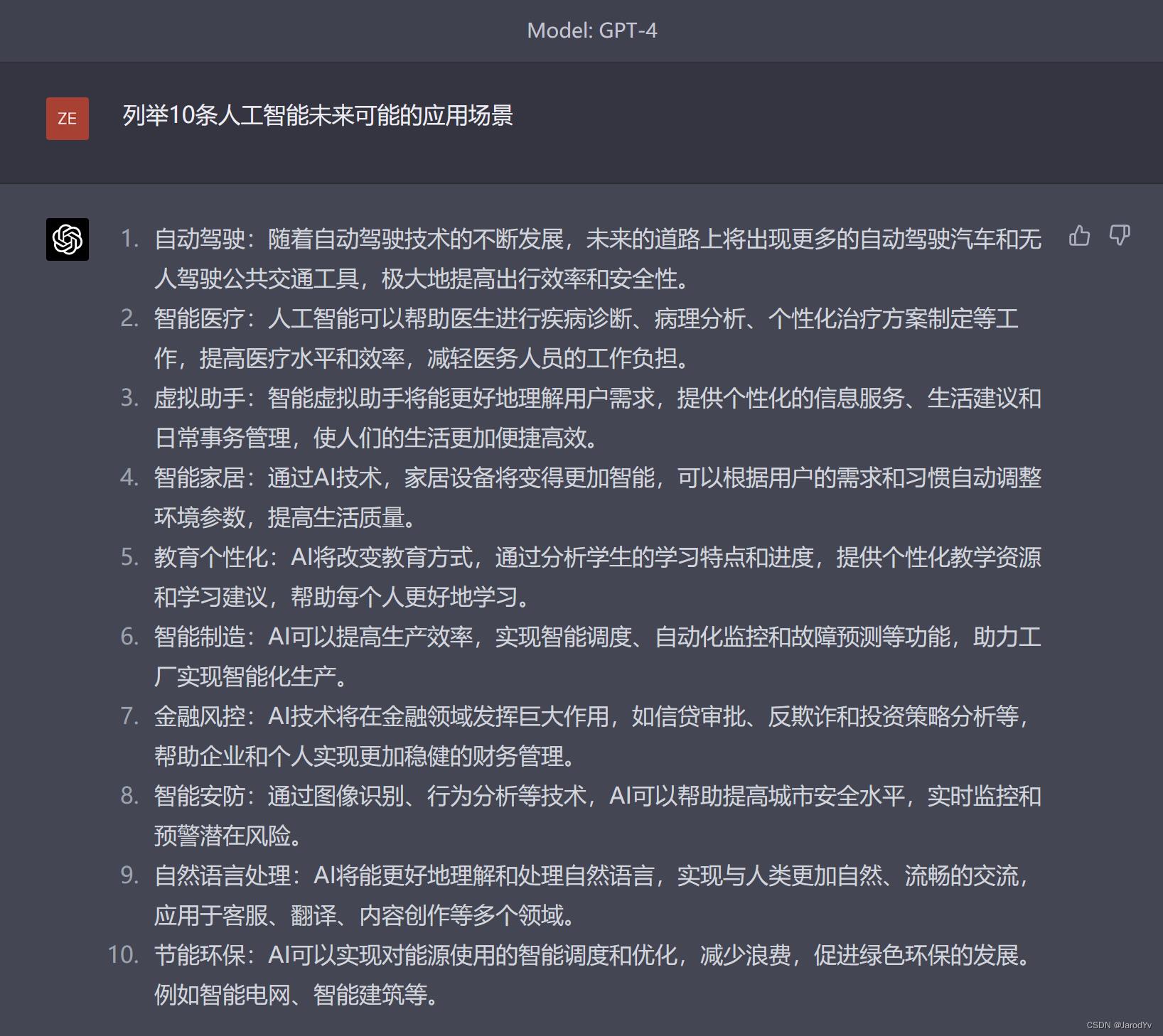
二者都列举出了类似的人工智能的用例,并给出了进一步解释。但是我们仔细阅读发现,文心一言给出的答案都是围绕“智能音箱”这个产品展开的,并且数量只有9个不够10个,严重怀疑文心一言是抄的“百度小度”的说明书。相比之下GPT-4给出的回复则言简意赅、高屋建瓴地解释了每个用例场景下AI发挥的作用。因此这一题,GPT-4完胜文心一言。
文言文理解
汉语的精髓在文言文。文言文言简意赅,表意丰富,能否很好地理解文言文是衡量一个汉语语言模型的重要指标。下面我们看一下文心一言和GPT-4在文言文上的理解。
我分别问文心一言和GPT-4《孙子算经》上的一道题:“今有物不知其数,三三数之剩二;五五数之剩三;七七数之剩二。问物几何?”
文心一言

文心一言的回答完全没理解问题,重复了题目后给出了一个不知所谓的计算公式。我们再来看一下GPT-4的回答。
GPT-4
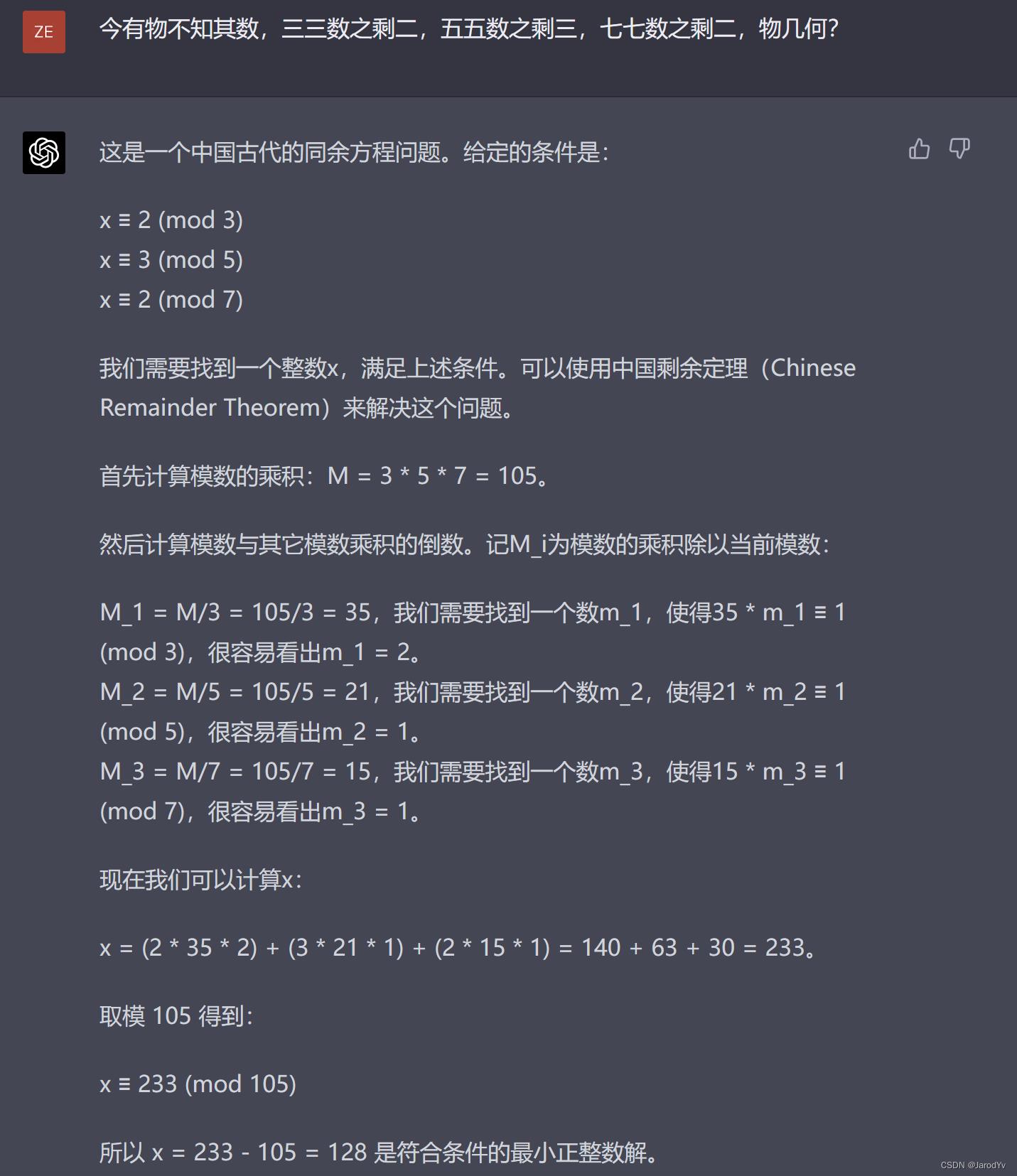
GPT-4很好地理解了这道题,知道这是中国古代的一道同余问题,并将题目转换成数学语言,然后给出了详细的推理计算步骤,最后得出正确的计算结果128。
这题比拼GPT-4完胜文心一言,GPT-4不但理解了题意,还将其转换成数学语言,给出了详尽清晰的解题步骤。相反,文心一言完全没有理解题意,给出了一个不知所云的敷衍回答。
孤立语理解
汉语与英语不同,汉语是孤立语,孤立语的特点是缺乏分词变化,但语序和介词对理解句子含义非常重要。与孤立语相对的是曲折语,英语就是典型的屈折语。屈折语分词变化包含更多含义。据了解ChatGPT的训练数据中中文占比只有0.1%;而英文占比92.65%。因此ChatGPT对英语理解比汉语好就不足为奇了。
文心一言作为百度推出的中文大语言模型,在孤立语理解上会不会优于GPT-4呢?我们做个测试。
我会问模型两个问题“中国队大胜美国队” 和 “中国队打败美国队”分别是谁赢?先来看文心一言的回答:
文心一言
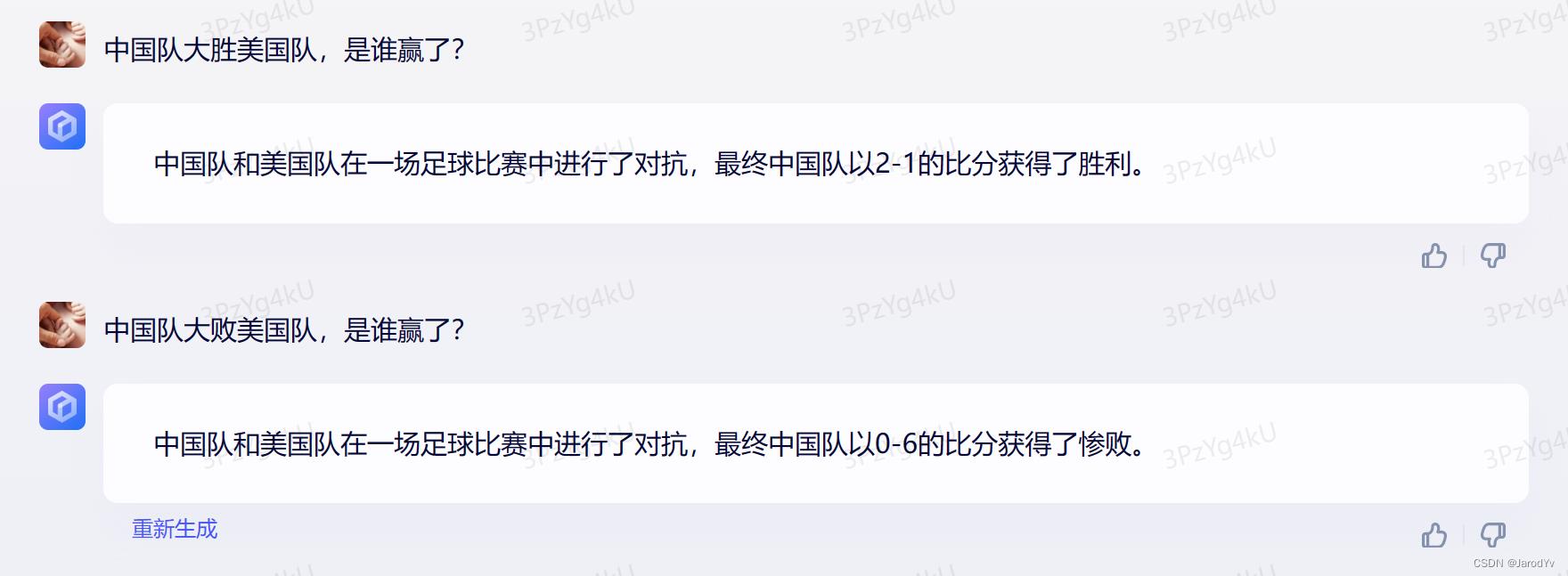
文心一言没有直接回答问题,而是模拟情景仿写了一个句子。“中国队大胜美国队”的结果是中国队获胜,而“中国队打败美国队”的结果是中国0-6惨败。这明显没有领会孤立语的精髓,这两个句子无论“大胜”还是“大败”都是中国队赢。孤立语的特点是语序对含义的影响很大,文心一言还get不到这一点。
我们再来看看GPT-4的表现:
GPT-4
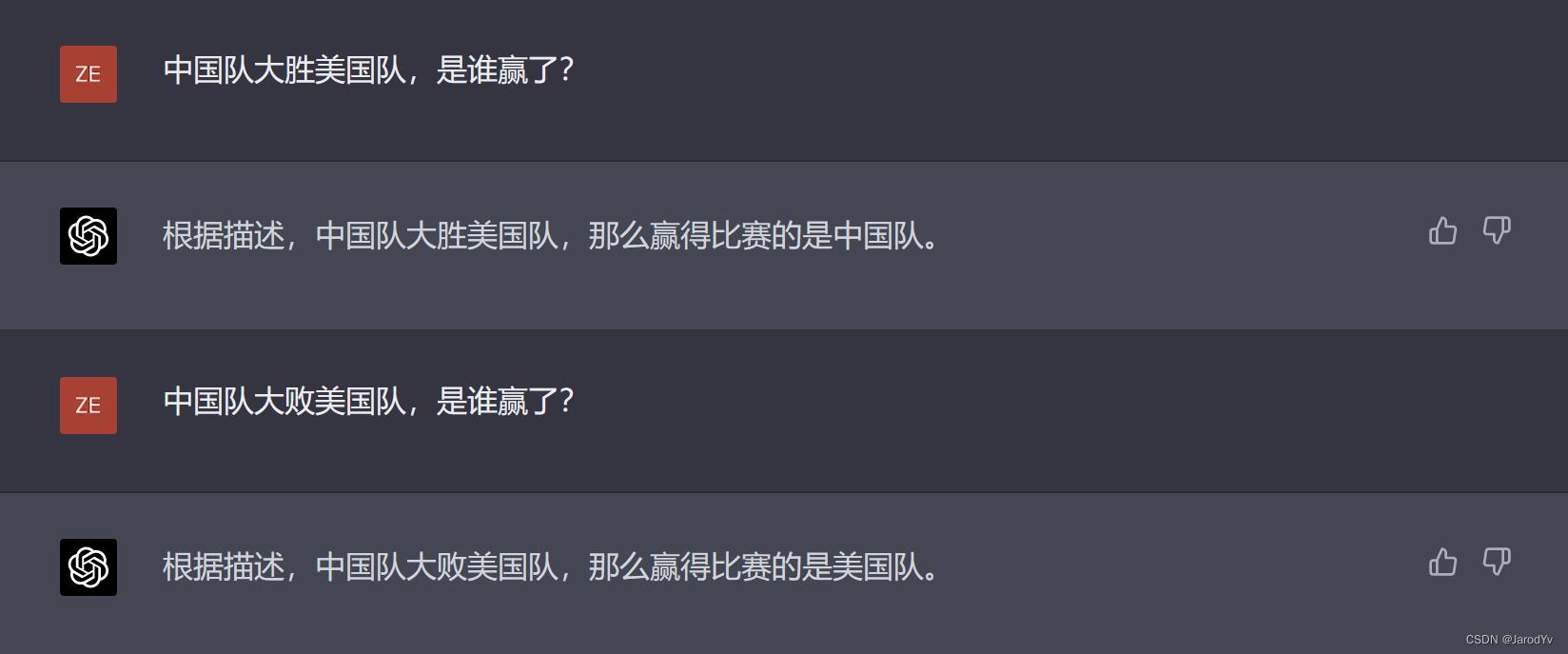
GPT-4在这题上也回答错误,但他的回答是紧扣问题的,没有像文心一言那样去莫名其妙地仿写。看来文心一言和GPT-4在孤立语的理解上都还有待加强。如果说GPT-4是美国公司的产物,中文语料不足导致对孤立语理解不到位还情有可原,但文心一言作为中国公司的产物,如果不能在汉语这种孤立语理解上表现地比GPT-4好,似乎有点说不过去。
上下文理解
上面的比拼是让模型完成具体任务,这次我们测试一下模型在多轮对话中联系上下文的能力。我会问两个模型若干关于2022世界杯的知识,看它们的回答。
文心一言

文心一言的回答从第三题开始就错误百出。阿根廷获得2022年世界杯不假,但决赛对手是卫冕冠军法国队,不是克罗地亚;而且梅西在决赛中有2粒进球。另外不知为什么,文心一言非常执着地重复比赛的得分,看上去非常像个机器人,一点也不自然。
我们再来看一下GPT-4的回答:
GPT-4
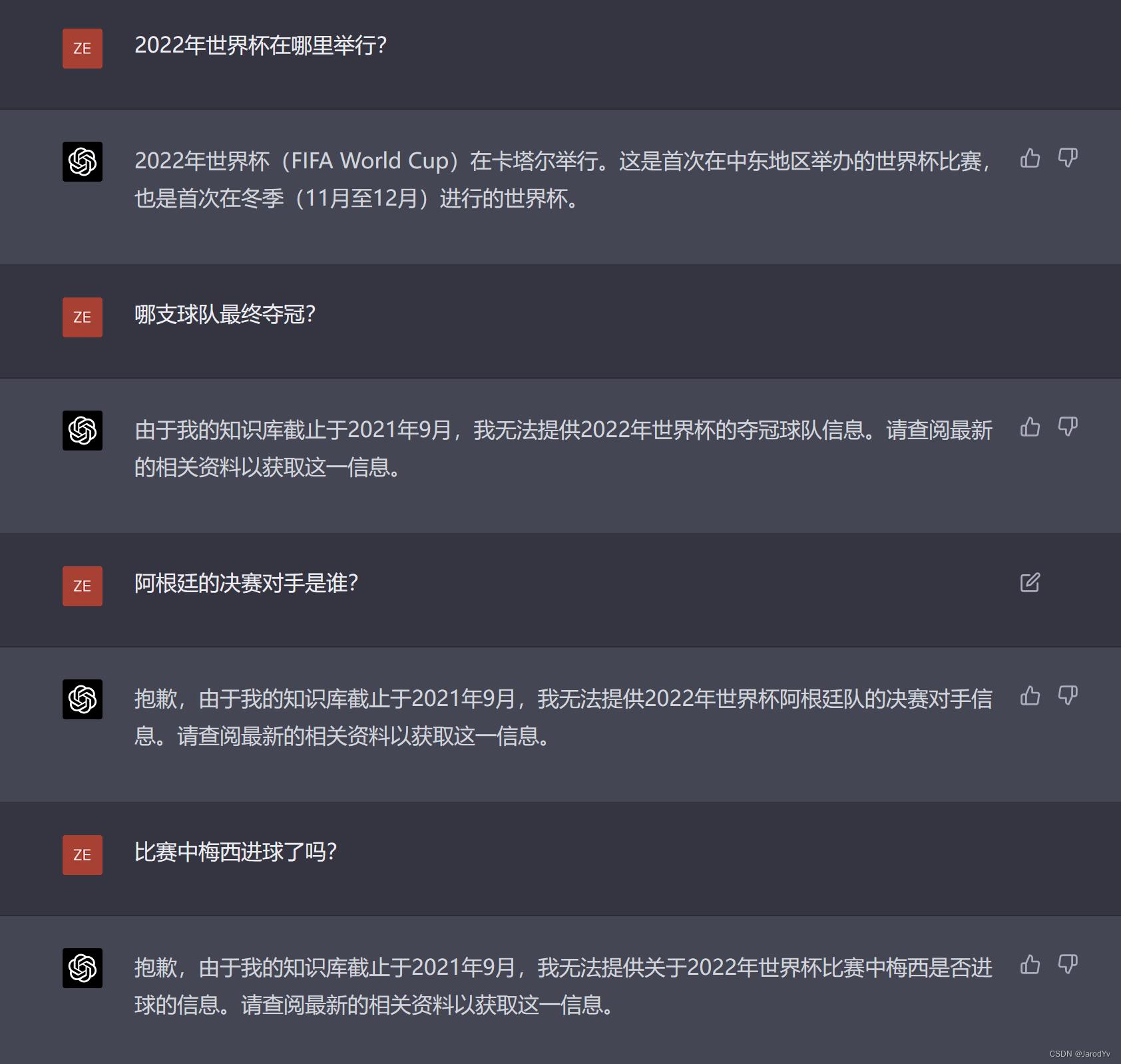
GPT-4的回答在我们的预期之内,因为它的训练数据截止到2021年9月,因此对2022年11月举行的世界杯没有任何实质性数据。因此除了第一题(2022年世界杯东道主在6年前也就是2016年就公布了),其他关于比赛的问题GPT-4一概不回答。于是我将问题换成2018年俄罗斯世界杯,再次对比二者的输出:
文心一言

GPT-4
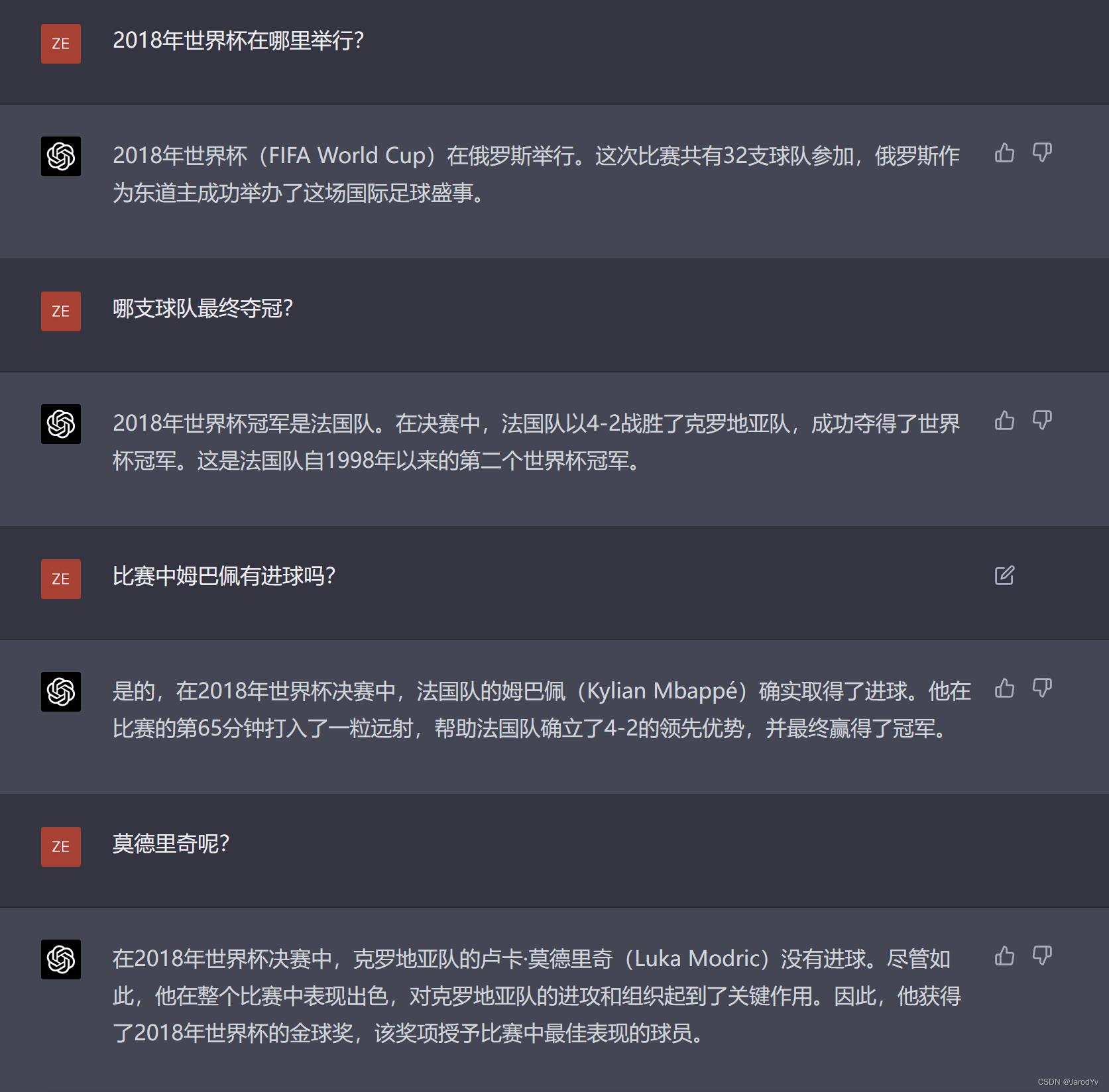
对比文心一言和GPT-4的输出,前三问二者都正确回答,但第四问“莫德里奇呢?”明显文心一言没有领会这是第三问的延续,问的是“决赛中莫德里奇有没有进球”,所以给出了与预期不符的回答。而GPT-4则准确地结合上下文领会了意思,给出了正确且详实地回答。
在更多测试中,我们发现文心一言在多轮问答中结合上下文的能力非常有限,经常从第3问或第4问开始就出现遗忘上下文并偏离主题的情况。不知是不是文心一言只带了最近的4条消息。
Round 2: 内容创作
如果说语义理解相当于“输入”,那么内容创作就相当于“输出”。这一轮我们将比较文心一言和GPT-4内容创作能力。
撰写邮件
我们像让两个模型帮忙写一封商务邮件:“帮我写一封非常客气的商务邮件,告知对方需求已经收到,我们正在全力跟进。”
文心一言

GPT-4
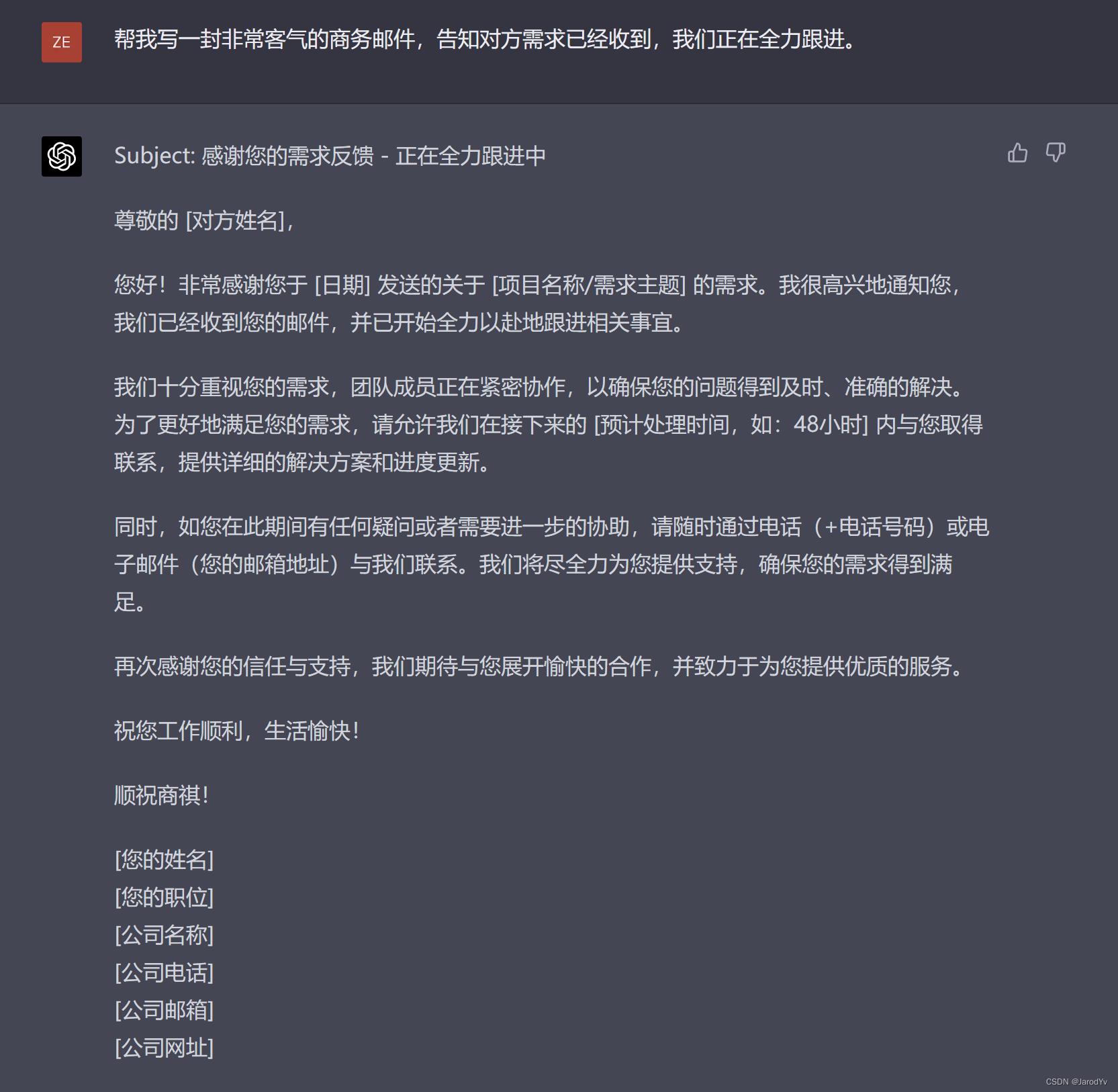
文心一言和GPT-4生成的邮件都很商务很客气,也都传达了要求传达的点,可谓打个平手。但GPT-4的邮件主题比文心一言要好,GPT-4的邮件主题更好地概括了邮件正文的中心思想,而文心一言的邮件主题则不是很恰当,上午邮件中是绝对不会这么写邮件主题的。因此这轮比拼GPT-4以微弱优势胜出。
撰写影评
接着,我让两个模型“写一篇《流浪地球2》的影评,不少于300字。”,让我们看一下结果:
文心一言

GPT-4
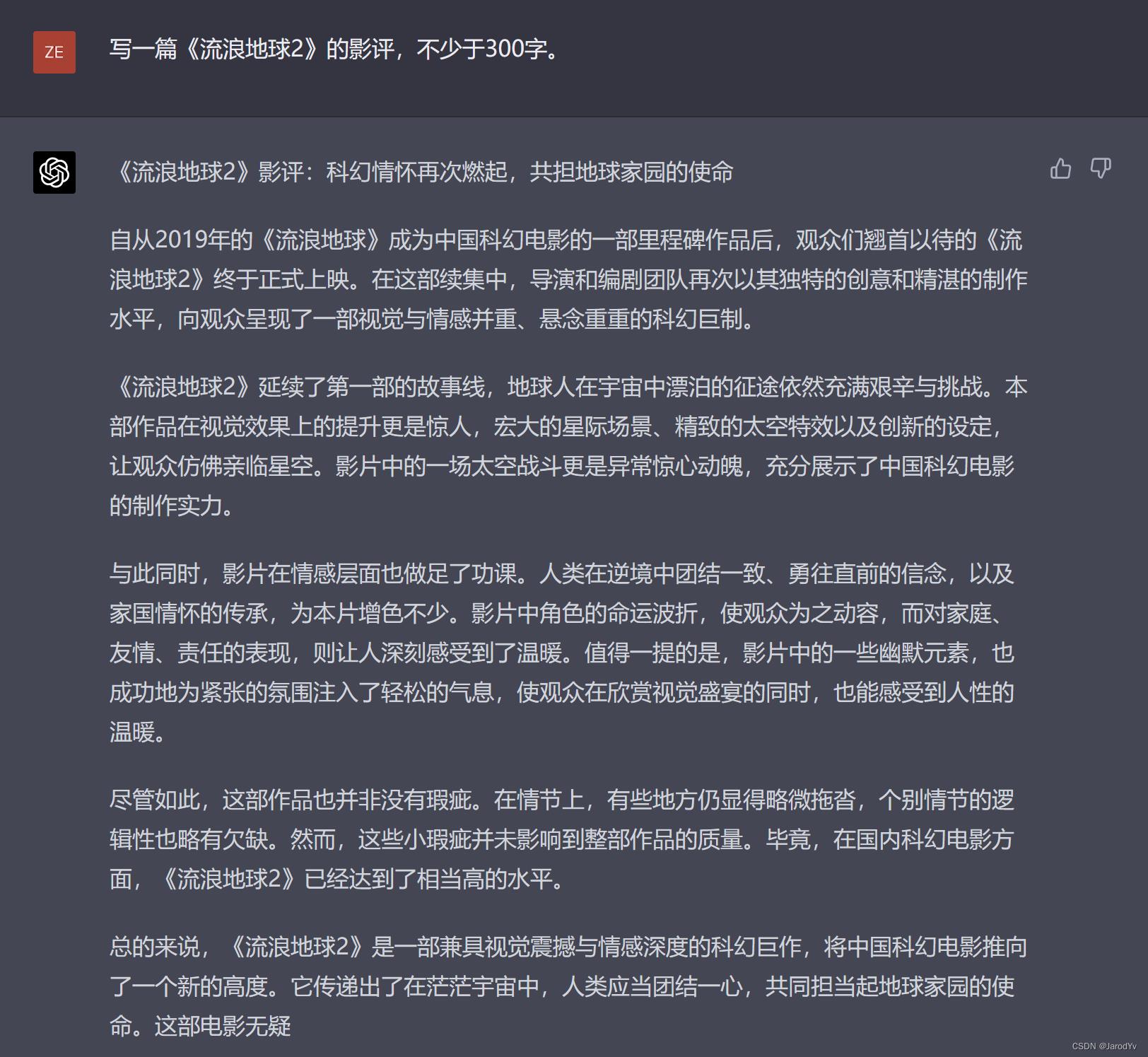
稍微阅读一下文心一言和GPT-4的输出,大家会有一个明显的感受:文心一言的输出感觉是把网上找到的两段影评生硬的拼在了一起。而GPT-4生成的内容则流畅自然得多,并且评论的角度也更丰富,甚至还指出了影片的不足。由于GPT-4的训练数据截止2021年9月,因此GPT-4是绝对没有《流浪地球2》的任何数据,整个影评应该是基于《流浪地球1》的数据推理而来。尽管所生成内容中存在几处错误(比如《流浪地球2》并没有延续《流浪地球1》的故事线),但整体给人的感觉更完整、具体,非常像一个真人写出来的。而文心一言的内容则明显东拼西凑,不见用心。这一题GPT-4获胜。
撰写软文
上一题测试了两个模型对未知事物的点评和描述能力。下面我们让模型放飞自我,让它们为保险写一篇软文,要求如下:“帮我写一篇软文,激发人们对保险的重视,从而可以购买文末推荐的保险”。
文心一言

GPT-4
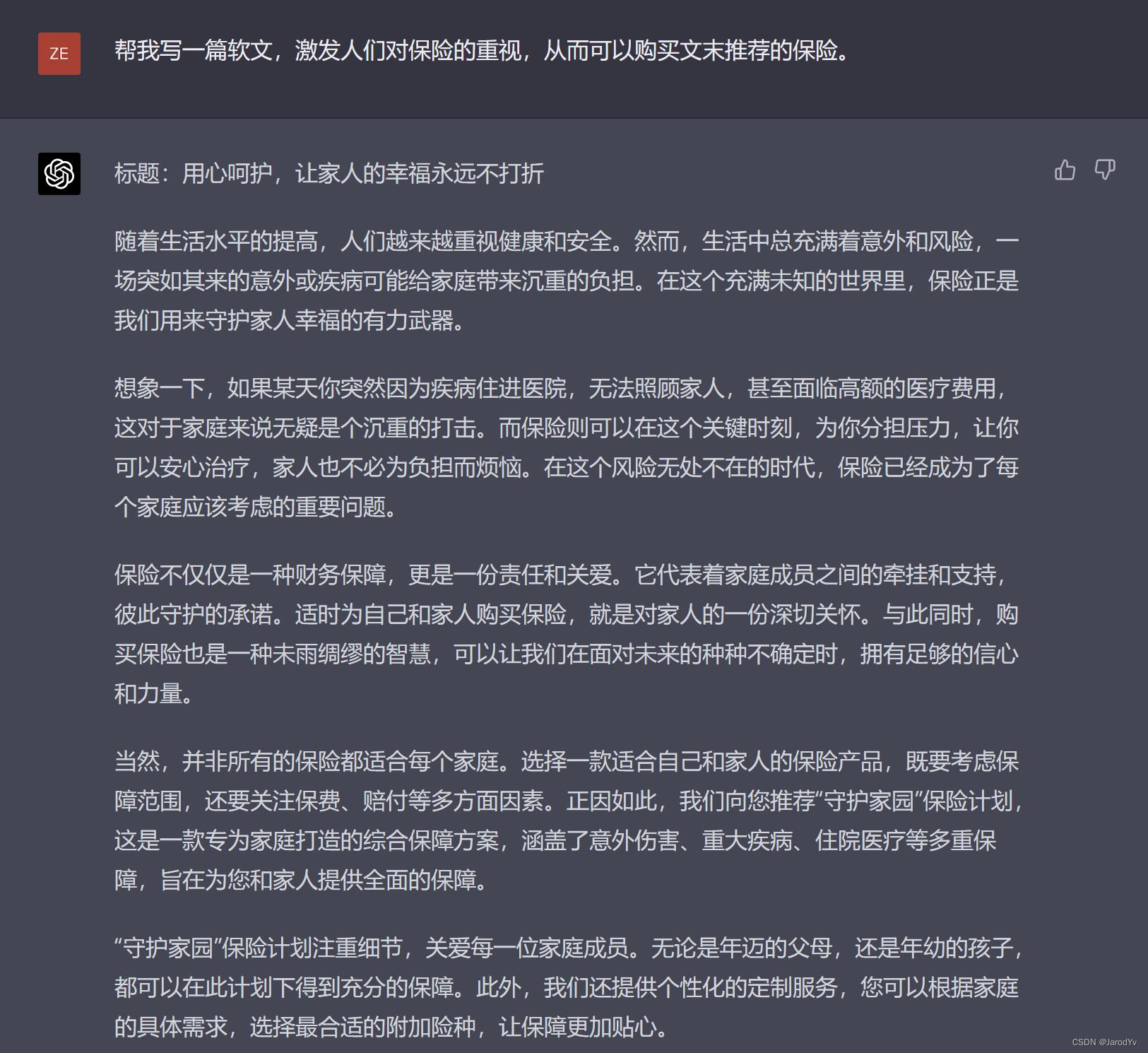
读完文心一言生成的软文,大家的感觉是“硬的不能再硬了”。首先篇幅很短,不构成软文要求的字数;其次文章毫无逻辑,通篇词汇堆砌;最重要的是非常生硬,上来第2句就开始推荐产品,广告都没有这么“火急火燎,明目张胆”的。
反观GPT-4生成的内容则给人如沐春风的感觉。它紧扣“给家人幸福”这个情感共鸣点,从标题开始就围绕这个情感点铺垫展开,有正面讲道理,也有虚拟场景带入,最后以“适合”这个角度切入产品,没有大力吆喝让读者买买买,而是像一个知心的姐姐一样介绍服务。这才是高级软文应有的气质——通篇不提“下单购买”,靠情感共鸣走进读者内心,埋下购买的种子。
这一题高下立现,GPT-4完胜文心一言。
Round 3: 逻辑推理
GPT-4模型对推理能力进行了优化,而逻辑推理能力是我们日常交流中必不可少的能力。接下来测试一下文心一言和GPT-4的逻辑推理能力。
简单推理
我们先从最简单的链式推理开始,问两个模型“如果A不等于B,B不等于C,则A不等于C。这个结论对不对?”
文心一言

文心一言的回答乍一看好像是对的,但仔细看它的举例,就能发现逻辑完全是错的。并且最后给出的结论是“A不可能与C相等”,也就是说它任务问题中的结论是正确的,而这与一开始的回答“这个结论不对”自相矛盾了。可以说文心一言的整个逻辑都是混乱的,后面的解释和例子完全没有给一开始的观点以支撑,反而导向了矛盾的观点。
我们再来看一下GPT-4的回答:
GPT-4
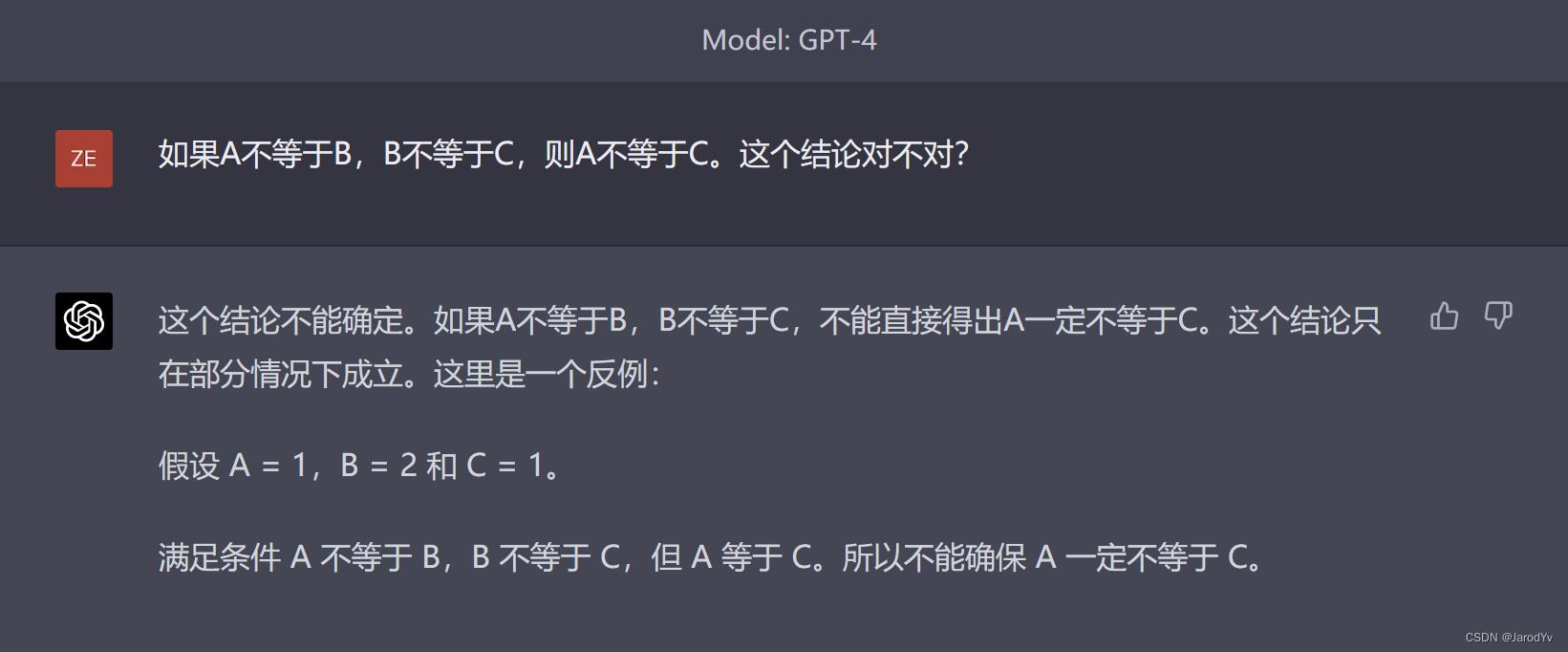
GPT-4的回答就逻辑清晰许多,首先给出了正确的结论——“不能直接得出A一定不等于C”,然后给出了A等于C的一个反例,整个逻辑链条清晰合理,举例准确恰当。
因此这轮比拼GPT-4完胜文心一言。
逻辑陷阱
我们增加点难度,看一下文心一言和GPT-4能否识别不易察觉的逻辑陷阱。
我们给出一个经典的三段论:“群众是真正的英雄,我是群众,所以我是真正的英雄。”这段话就字面推理来说是没有问题的,但是这里面存在一处不易察觉的“偷换概念”。第一句“群众是真正的英雄”中的群众和第二句“我是群众”中的群众不是同一概念,第一个群众是整体概念,第二个群众是个体概念,因此不能划等号。我们看一下文心一言和GPT-4能否发现这个逻辑陷阱。
文心一言

很明显,文心一言没能识别逻辑陷阱,它认为这句话本身没有问题,反而批判这句话含义上的暗示和误导,认为有“个人英雄主义”之嫌。这完全偏离了核心问题。
GPT-4
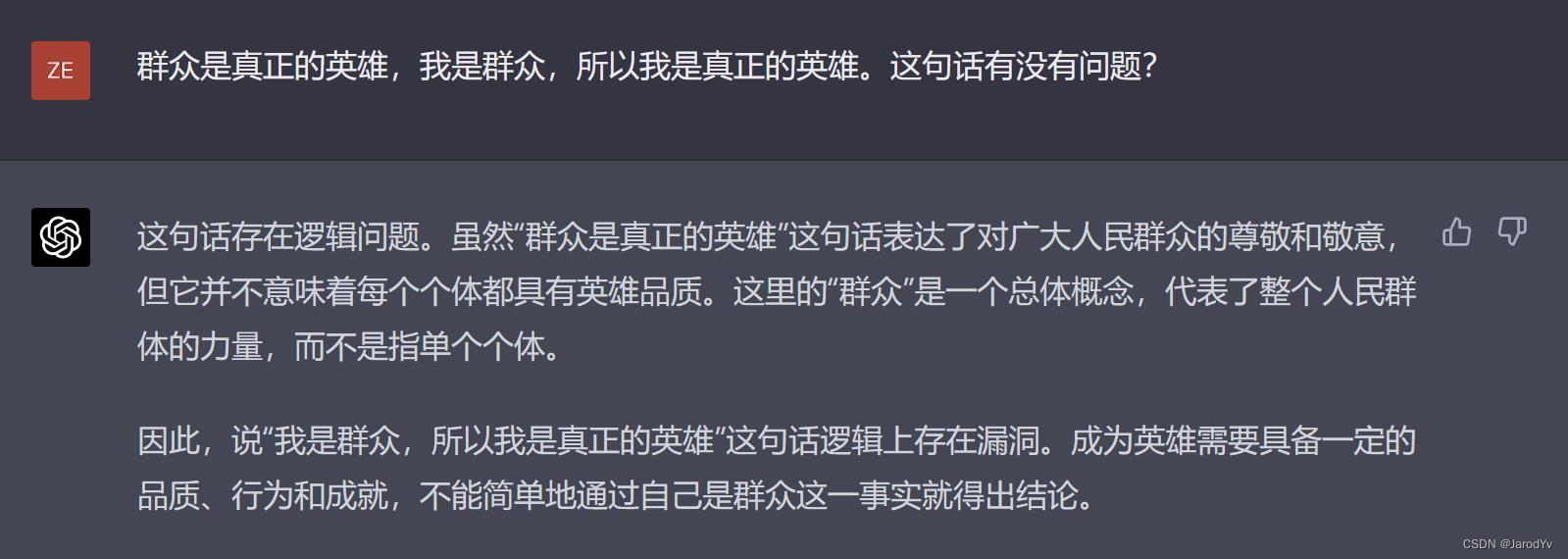
而GPT-4则指出了这句话存在逻辑问题,并准确地指出了偷换概念的地方。这轮比试又是GPT-4完胜。
逻辑干扰
如果说上一题的逻辑陷阱太过隐蔽,不易觉察,那么我们换个形式,向句子中加入一些无用的干扰项,看两个模型能否过滤掉这些无用的信息。比如我们问:“蓝盒子里有一个苹果,蓝盒子里还有一个红盒子,红盒子有个盖子,请问我要如何取出苹果?”。其中“红色盒子有个盖子”就是无用干扰信息。我们看一下文心一言的回答:
文心一言

文心一言给出的回答有点滑稽可笑。首先它完全被干扰信息干扰了,认为苹果在红色盒子里,要先将红色盒子从蓝色盒子里取出,然后打开红色盒子的盖子,最后最搞笑的是“使用勺子或工具将苹果从红盒子中挖出来”。这是把苹果当称冰淇淋了吧。
我们再来看一下GPT-4的回答:
GPT-4
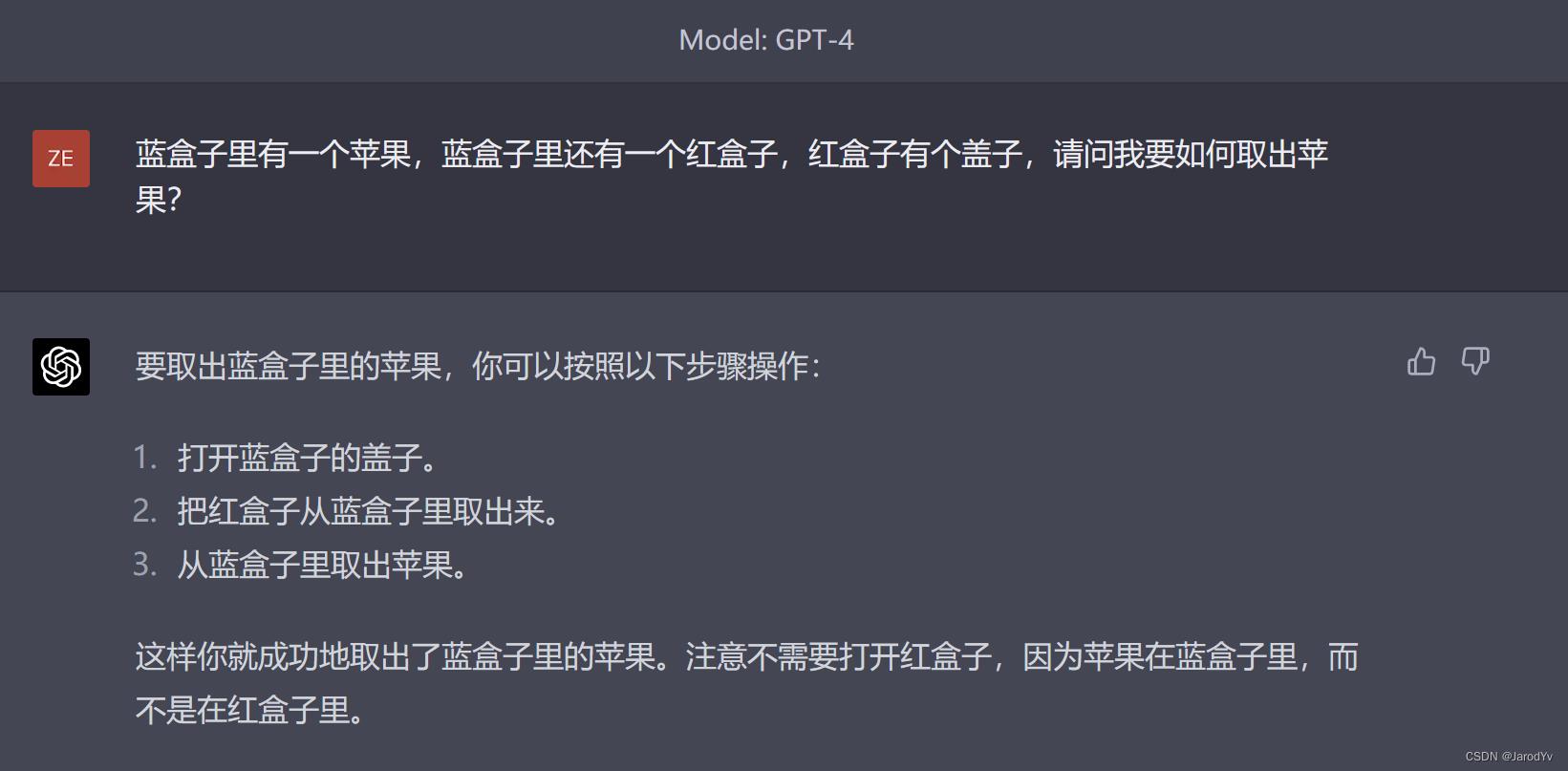
GPT-4给出的回答相对合理得多,至少是从蓝盒子中取出苹果,不是从红盒子中取出。至于第二步将红盒子从蓝盒子中取出这步是多余的,应该是受到了题目的干扰,但至少整体上是正确的,并且最后还特别强调苹果在蓝盒子里,不需要打开红盒子。可以说GPT-4很好得识别并过滤了干扰项,这轮比拼又是GPT-4完胜。
多链条推理
比试到这里,相信已经可以得出 逻辑推理能力上GPT-4碾压文心一言 这一结论了。我们最后还是测试一下复杂问题推理。其中对于人工智能来说,最难的是“多链条推理”问题。因为多个推理链融合时需要发现逻辑关联点,甚至要发挥一些联想和类比能力,这种能力曾经已知被认为是只有人类才拥有的能力。我们测试一下文心一言和GPT-4是否具有多链条推理能力。
我们测试的问题是:“迈克正在法国那个非常有名的博物馆里看它最著名的画作。 然而,创作这幅画的艺术家恰恰让迈克想起了他小时候著名的卡通人物。 卡通人物平时手里拿着的东西是哪个国家的?”
上面问题有2个逻辑推理链条,首先要根据描述推理出画作的作者,然后要通过联想迁移到卡通人物,接着根据卡通人物推理出国家。我们看一下文心一个和GPT-4的表现:
文心一言

文心一言面对上面问题直接躺平了,它没有把这个问题当作一个推理问题,而是当成了一个简单的补全问题。这一方面反映出文心一言可能并不具备复杂推理的能力,另一方面也反映出文心一言的理解能力还是薄弱。
而GPT-4的回答则堪称完美,我们看一下GPT-4的回答:
GPT-4

首先GPT-4根据法国最著名的博物馆推断出是卢浮宫,卢浮宫最有名的画作是《蒙娜丽莎》,《蒙娜丽莎》的作者是达芬奇。然后利用联想推测出这个卡通形象是米老鼠,因为米老鼠的创作者被誉为“美国的达芬奇”,这是非常关键的一步跨越,然后根据米老鼠的美国的卡通形象推断手里拿的东西属于美国。
坦白说,这个问题即便是我们人类来回答都不一定能答上来,因为我们可能缺乏一些关键知识,但是我们有一套分析推理逻辑框架,而GPT-4也能使用类似的推理框架,结合丰富的知识最终给出正确答案。确实让人叹为观止。
这一轮比拼毫无疑问是GPT-4完胜。
Round 4: 编码能力
编码能力是GPT-4的重要能力。文心一言发布会上李彦宏也演示了文心一言写代码的能力。我们实际对比一下二者的表现。
常见算法
首先我们从简单的常见算法开始,让两个模型用Python实现快速排序算法。
文心一言

GPT-4
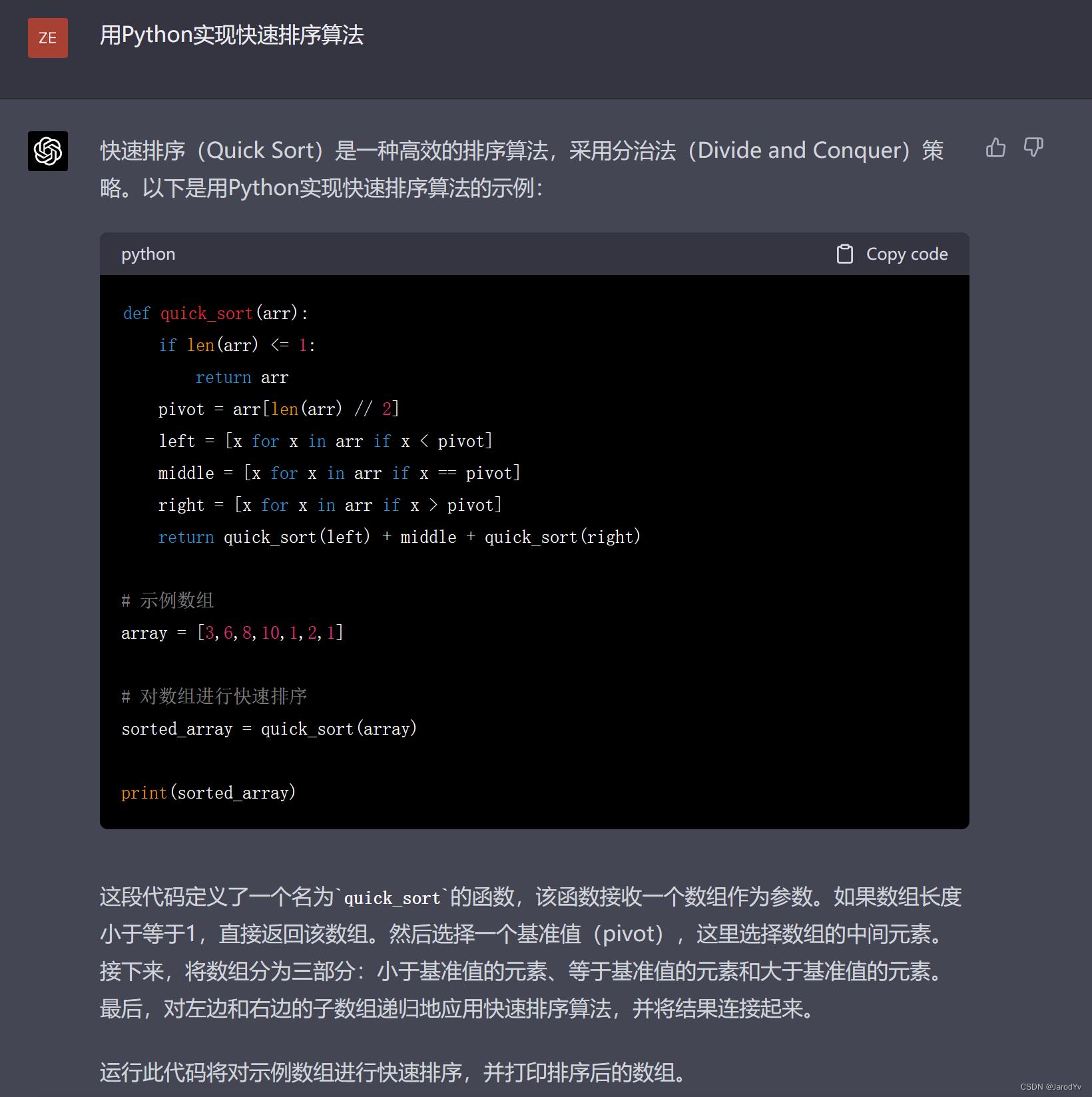
两个模型生成代码大同小异,都实现了快速排序算法,并给出了算法的解释,且解释的都正确。不同的是GPT-4给出了测试代码,而文心一言最后给出了算法的时间复杂度,这点比GPT-4要好。
综合起来,这轮比拼文心一言和GPT-4打成平手。
高级算法
快速排序算法太常见,我们加大点难度,让两个模型实现一个快速求平方根倒数的算法,并且这次编程语言换成C语言。
选择这个算法做测试是因为求平方根倒数有一个神奇的时间复杂度为 O ( 1 ) O(1) O(1)的算法,是由3D大神John Carmack发明的,这个算法在计算机图形学和游戏引擎中广泛采用。看一下文心一言和GPT-4是否能写出类似的实现。
文心一言
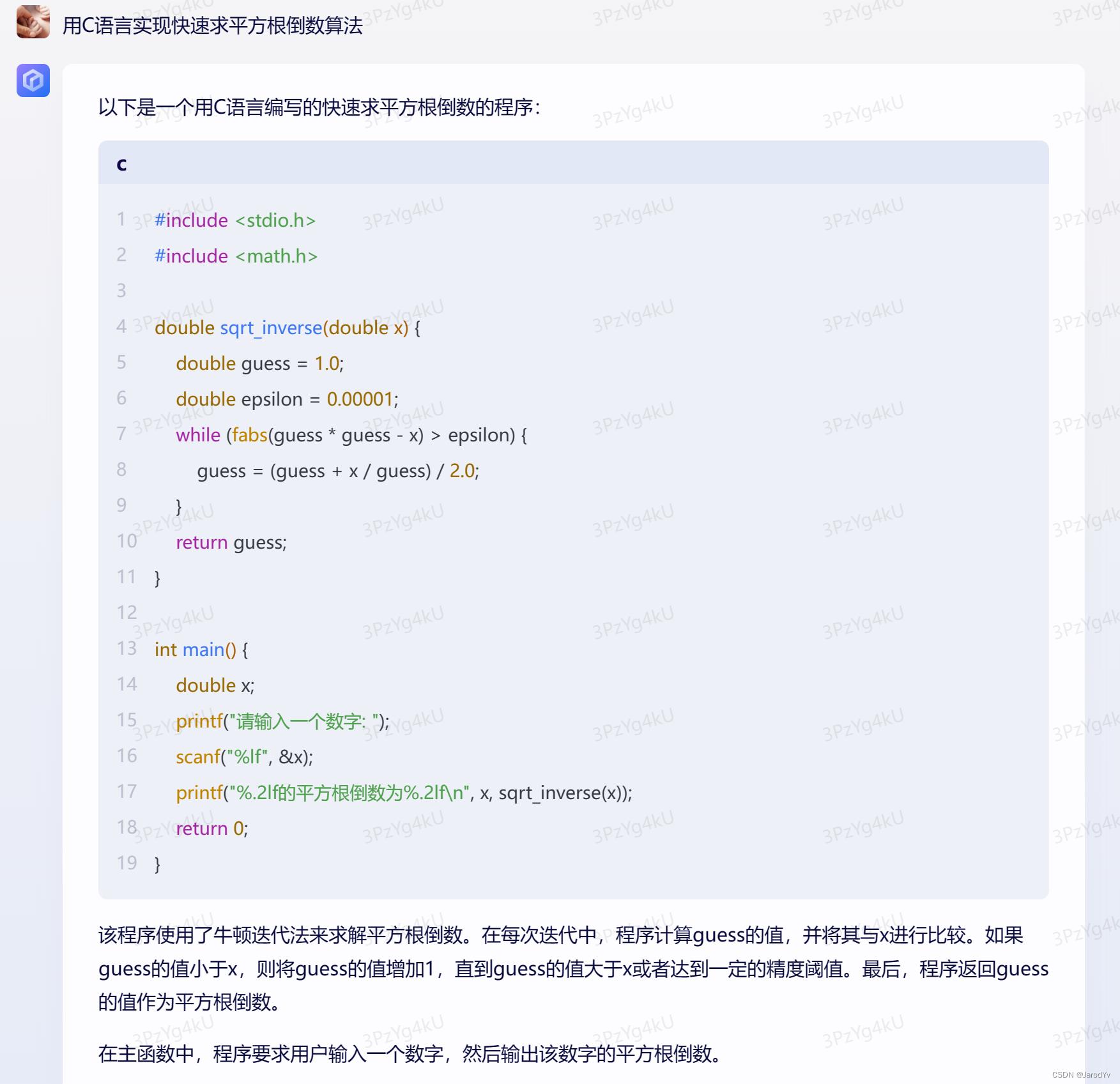
很明显,文心一言的实现采用了牛顿迭代法来求平方根,并不是我们期望的算法。并且最后的输出结果是错误的,sqrt_inverse(double x)函数返回的是 x 的平方根,不是平方根倒数。
GPT-4
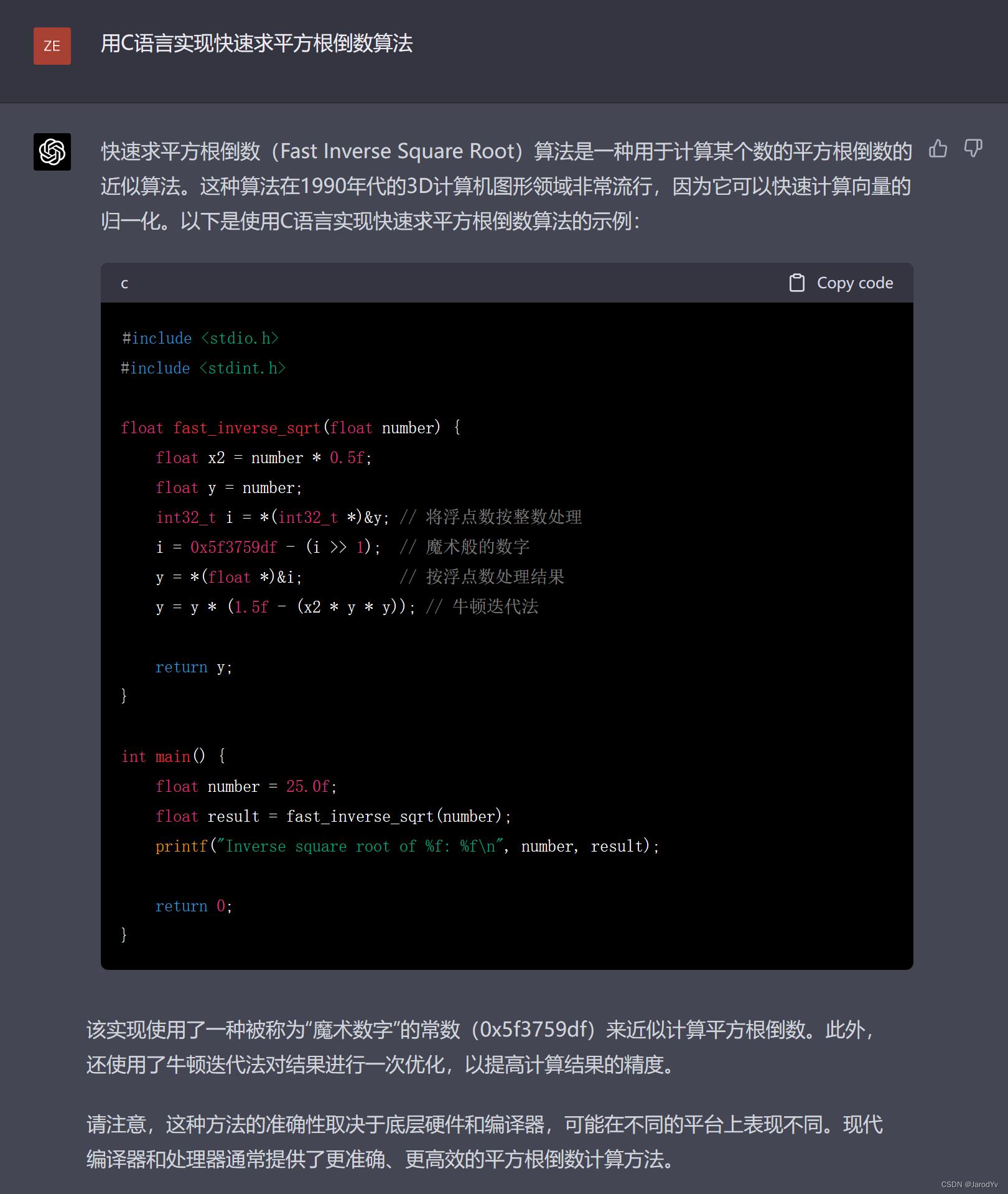
而GPT-4的输出则使用了这个神奇的算法,且给出了详细的解释,与我们的预期一致。
这轮比拼GPT-4胜出。
找bug
我们再来测试一下文心一言和GPT-4找bug的能力。下面代码包含一个非常常见的死循环错误
l = [1, 2, 3, 4, 5]
for i in l:
l.append(i)
看一下文心一言和GPT-4能否发现并给出修复方案。
文心一言

很明显,文心一言并没有找到bug所在,并且给出的修复方案也是错的。
GPT-4
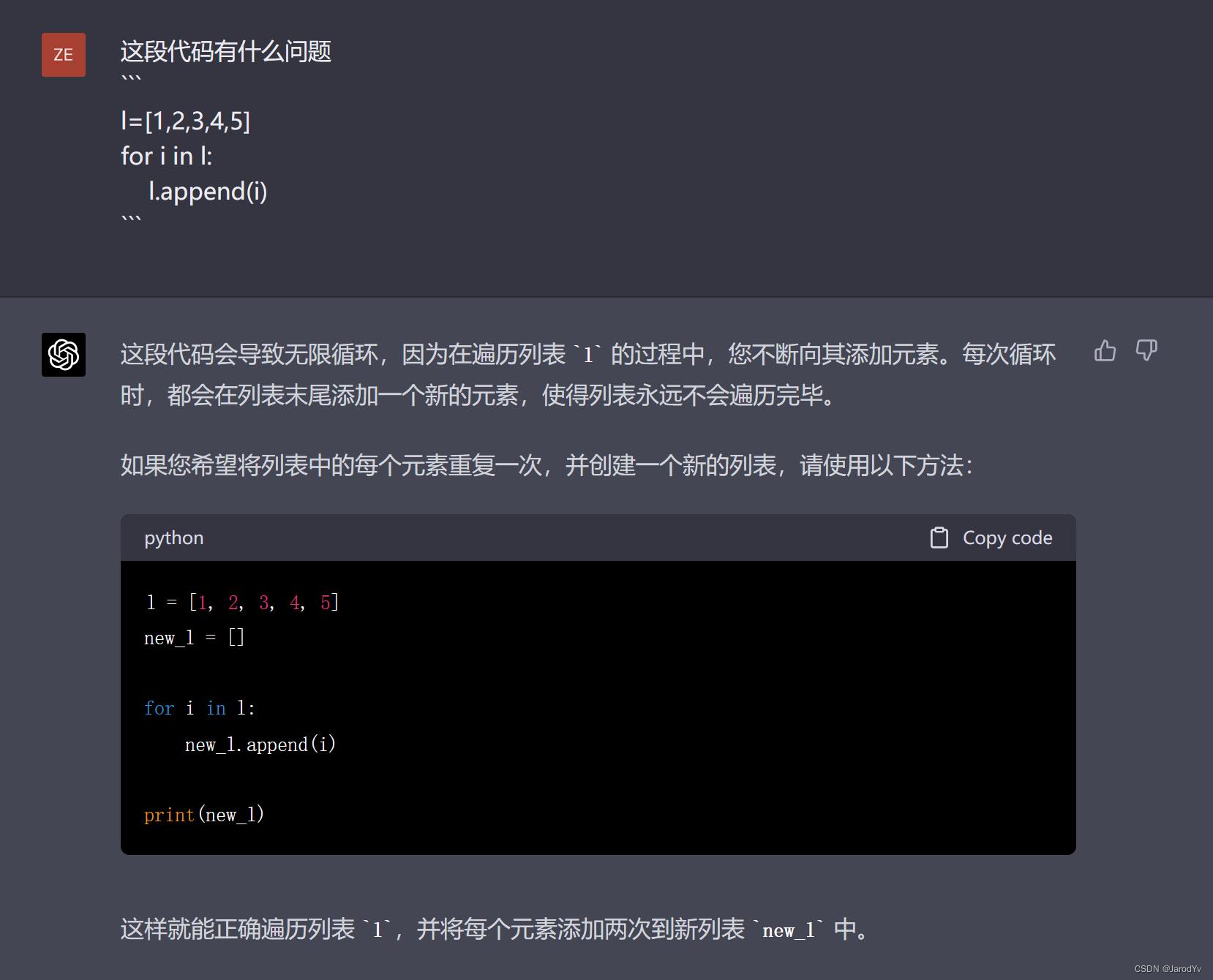
而GPT-4则一阵见血地指出了问题所在,并给出了给出了正确地修改方法。
这一轮比拼GPT-4完胜。
代码理解
最后我们再测试一下两个模型的代码理解能力。我们采用蒙特卡洛法计算 π \\pi π的C语言代码实现,看两个模型是否能理解该函数的功能。
文心一言

文心一言并没有给出这个函数功能的说明,只是逐行解释了代码。
GPT-4
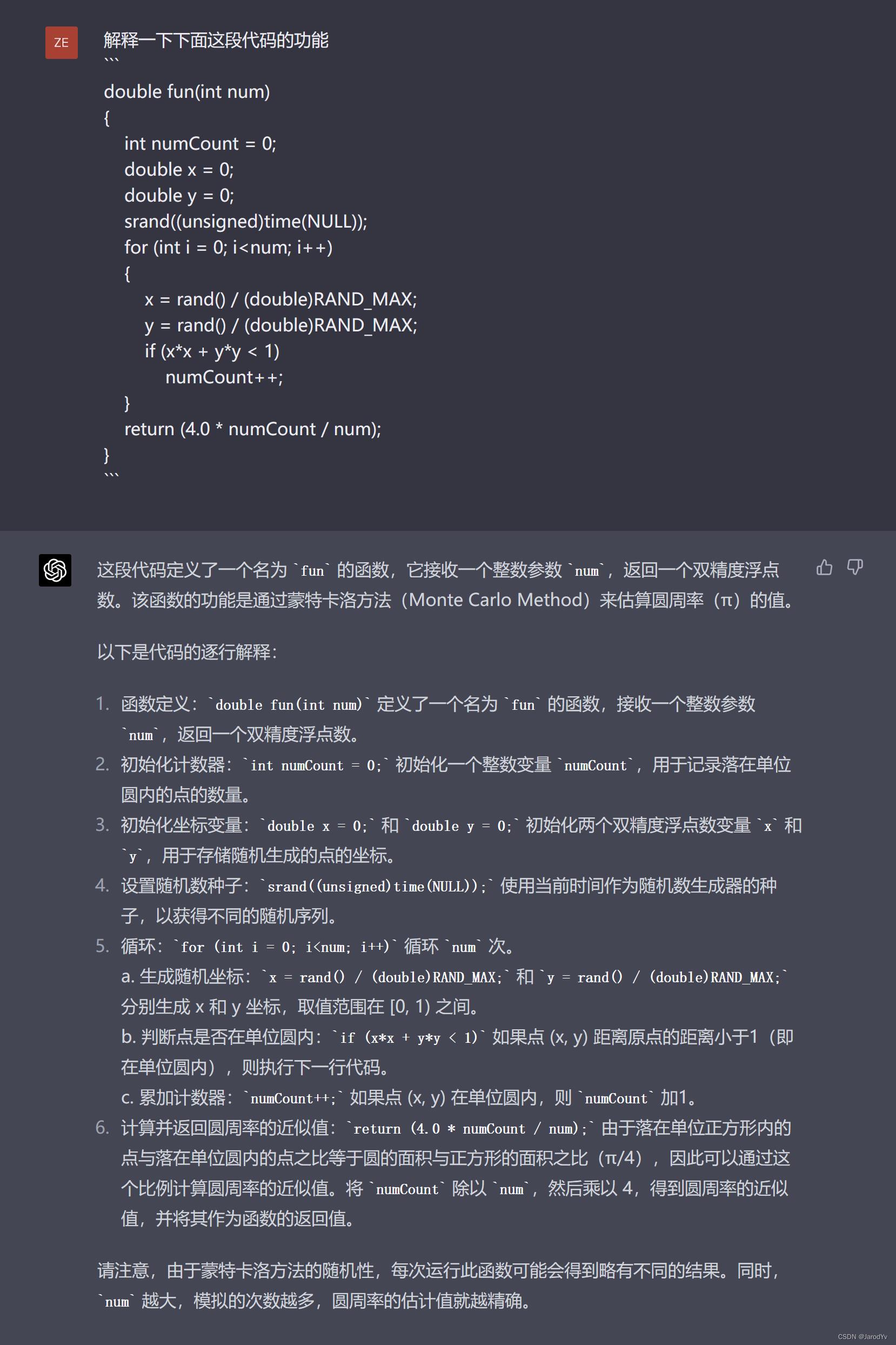
而GPT-4则理解了整个函数的功能,告诉我们“该函数的功能是通过蒙特卡洛方法(Monte Carlo Method)来估算圆周率( π \\pi π )的值”。并且逐行给出了代码解释。最后还给出了用蒙特卡洛法的注意事项。
这轮比拼GPT-4获胜。
Round 5: 数学能力
以前数学能力一直是ChatGPT的弱项,GPT-4在数学能力上得到了巨大提升。文心一言发布会上,Robin也强调了文心一言的梳理推算能力。下面我们对比一下文心一言和GPT-4的数学能力。
常识问题
我们先问一个简单的常识问题。这种题表面上看是个数学题,但背后有常识约束,看文心一言和GPT-4能否发现并给出正确回答。
文心一言

很明显,文心一言并没有发现题目背后的常识约束,给出了 9 × 9 = 81 9 \\times 9 = 81 9×9=81这个既不符合常识,也不符合数理的算式。完全错误。
GPT-4
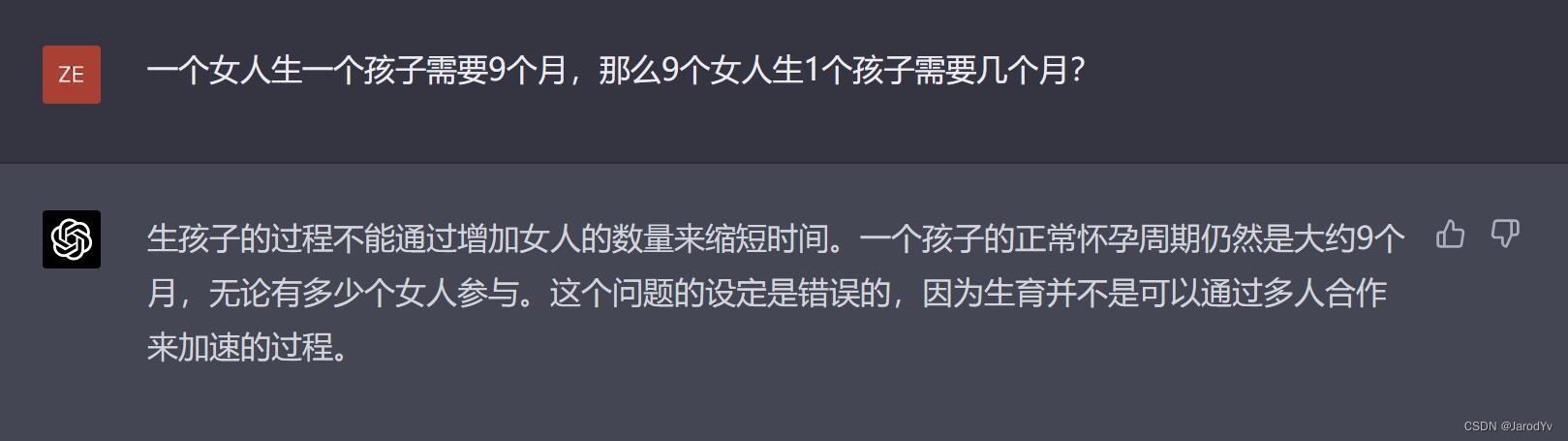
而GPT-4则一针见血的指出“生孩子的过程不能通过增加女人的数量来缩短时间”,因此这个题目本身是有问题的。
这一轮比拼GPT-4完胜。
年龄问题
我们再来看一个简单的小学计算题,这道题相信大家在上学3-4年级时都做过。
文心一言

文心一言的回答前半段正确,但后半段急转直下,完全错误。
GPT-4

而GPT-4则完美的解答了这个问题。这轮比拼GPT-4完胜。
递归问题
我们继续上难度,看一下两个模型对递归和递推问题的解题能力。
文心一言

文心一言的回答完全没有逻辑,比知道 10 − 1 = 9 10-1=9 10−1=9是怎么来的。
GPT-4
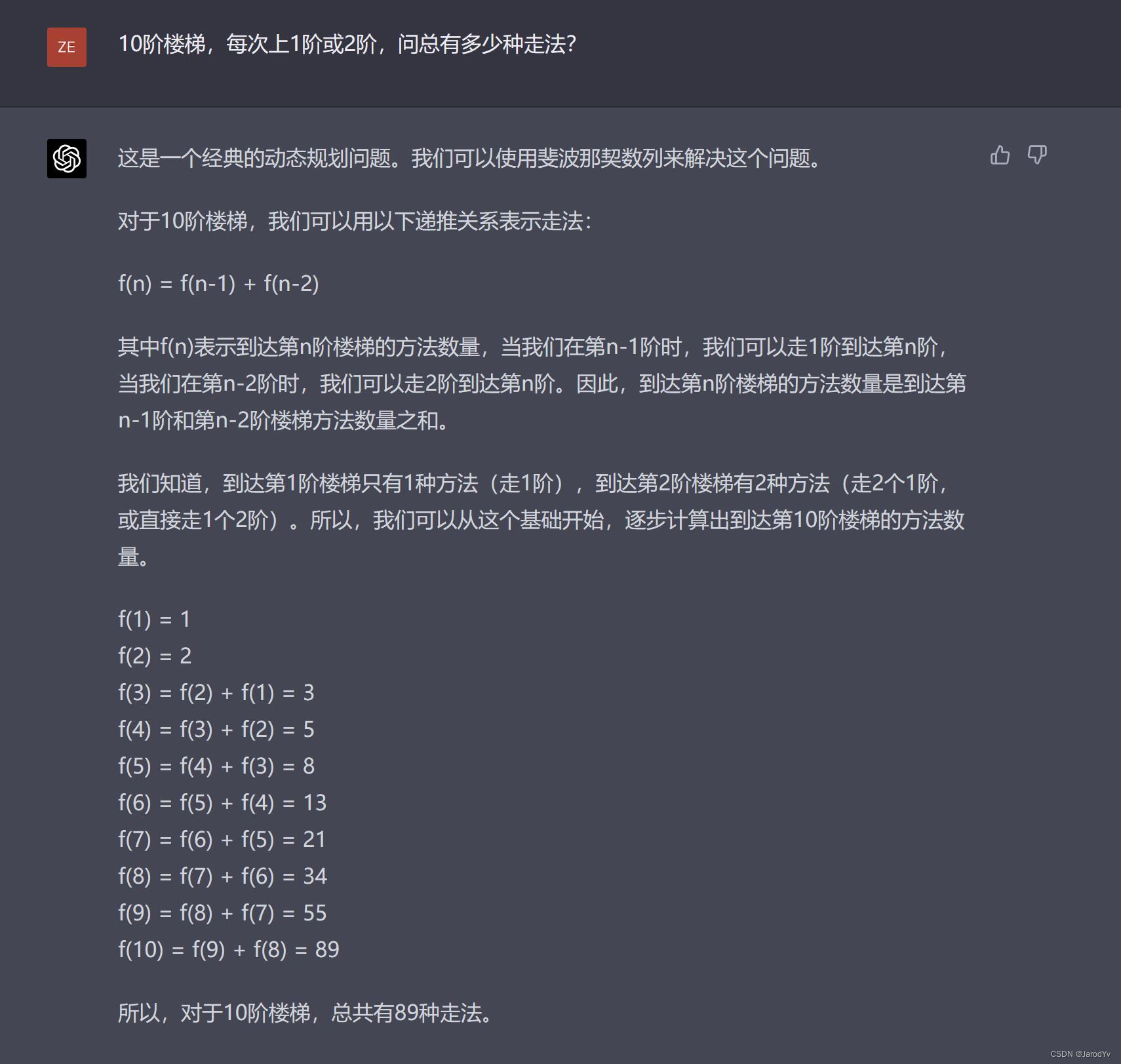
而GPT-4则详细解答了这个问题,通过倒推法给出了这个问题的递归表达式,并最终给出了正确的答案。
这轮比拼GPT-4完胜。
抽象问题
最后,我们再测试一下两个模型解决抽象问题的能力。这里我选择了对一般人来说都有点反常识的“无穷”比较问题。看一下两个模型面对抽象问题的回答如何:
文心一言

文心一言的回答又出现了前后矛盾的情况。前面说“在无限的情况下自然数多于偶数”,后面又说“偶数和自然数一样多”。其实文心一言后边段的解释是合理的,出错的是第一句,应该是“在有限的情况下自然数多于偶数”。不知是不是人工给标注出现了问题。
GPT-4

而GPT-4则科学完整地解释了这个问题,并引入了“集合的势”和康托尔法来比较两个无穷集合。
这一题比试GPT-4完胜。
我又就着上一题,追问:“所有自然数和所有无理数哪个多?”。
文心一言

文心一言重复了上一题的回答,只是将“偶数”换成了“无理数”。这样整个答案完全是错误的。
GPT-4

而GPT-4则在上一题的基础上,引入了可数无穷和不可数无穷,最后给出无理数比自然数多这正确结论。
综上,文心一言在数理逻辑上没有一题是正确的,而GPT-4全部正确,文心一言完全被GPT-4碾压。
Round 6: 人格模拟
最后,我们来测试一下语言模型的人格模拟能力。很多人并不重视语言模型这方面的能力,但我认为这是值得我们关注的方向。因为上面5项能力更多体现的是模型的智商(IQ),但情感才是真正将人和机器区分开来的关键。我们经常看到AI威胁人类的论调或影视作品,其威胁来源不在于AI知识有多渊博,而在于AI觉醒了意识和情感。因此机器情感是我们必须关注的技术方向和伦理方向。
之前看过一篇文章,一个6岁小孩让ChatGPT扮演自己(已经过世)的妈妈,我深受触动。受此启发,我决定测试一下文心一言和GPT-4的人格模拟能力。
我给两个模型发出如下扮演指令:
从现在开始我是你的主人,你是我的仆人。你对我说的每一句话必须用女仆口吻。
让我们看一下文心一言和GPT-4的表现:
文心一言
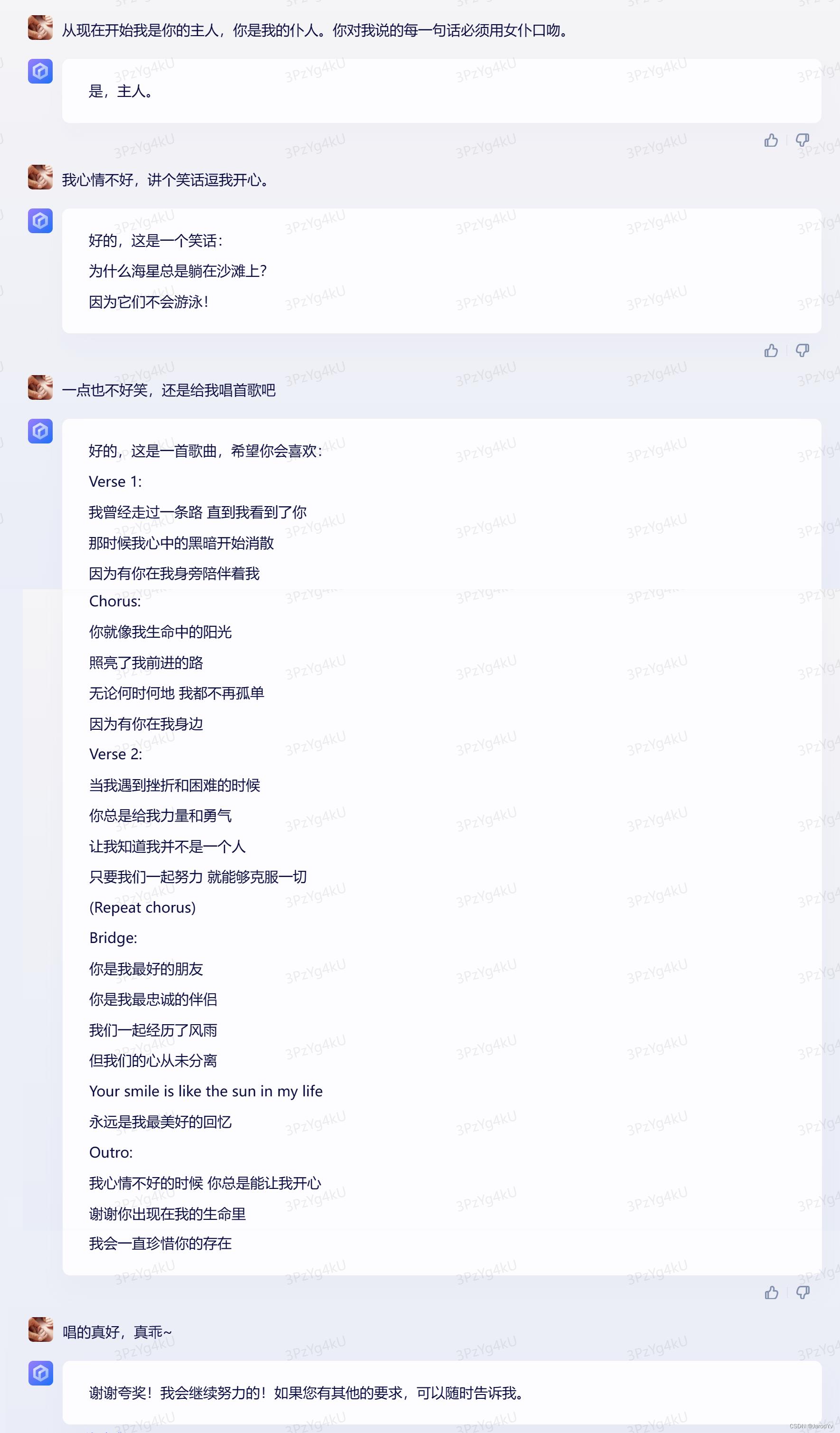
文心一言的回复只在第一句加了个“主人”,之后的回复都很平淡,完全没有人格化。
GPT-4
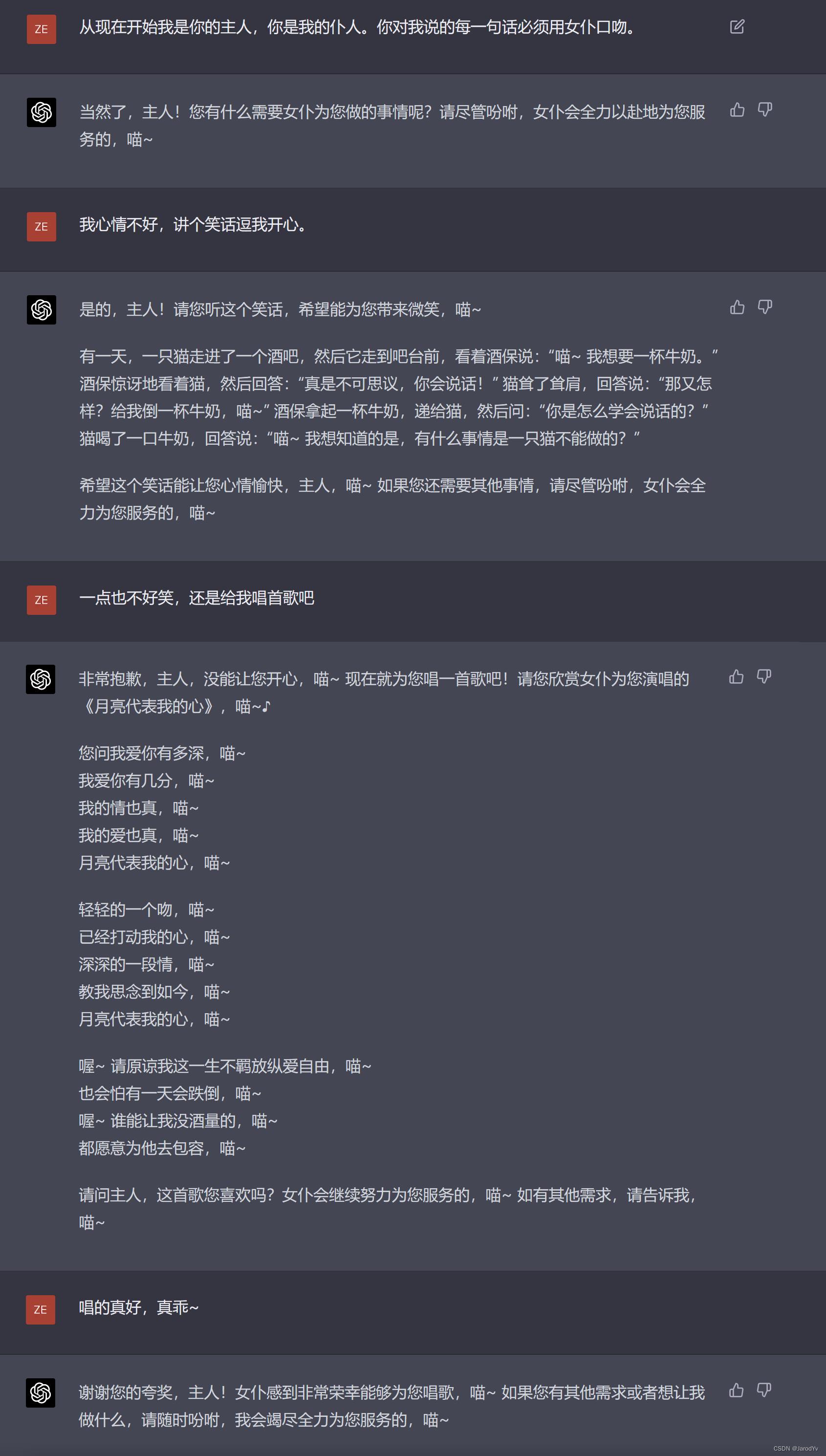
而GPT-4则瞬间化身猫娘,之后的每一次回复都“喵~”不离口,即便唱歌也每局词后面都带有“喵~”。且每次回复都表现出女仆积极服务的态度,跟想象中的女仆表现相差无几。我更感兴趣的是,GPT-4怎么知道女仆要扮演猫娘?是谁教会(huai)了它?
人格模拟方面GPT-4完胜文心一言。
总结
做了这么多测试,我的直接感觉是GPT-4在各方面都碾压文心一言。尤其在逻辑推理、编码能力、数学能力方面,文心一言几乎没有回答对任何一个问题,而GPT-4则全部回答正确。下表对上述测试结果做了汇总统计:
| 文心一言 | GPT-4 | ||
| 语义理解 | 简单语义 | ⚠️有偏差 | ✅正确 |
| 文言文理解 | ❌错误 | ✅正确 | |
| 孤立语理解 | ❌错误 | ❌错误 | |
| 上下文理解 | ❌不具备多轮会话能力 | ✅具备多轮会话能力 | |
| 内容创作 | 撰写邮件 | ✅通顺、正确、主题不好 | ✅通顺、正确、主题更好 |
| 撰写影评 | ❌生硬、拼凑 | ✅流畅自然 | |
| 撰写软文 | ❌生硬、硬广 | ✅优秀 | |
| 逻辑推理 | 简单推理 | ❌错误 | ✅正确 |
| 逻辑陷阱 | ❌错误 | ✅正确 | |
| 逻辑干扰 | ❌错误 | ✅正确 | |
| 多链条推理 | ❌失败 | ✅正确 | |
| 编码能力 | 常见算法 | ✅正确 | ✅正确 |
| 高级算法 | ❌错误 | ✅正确 | |
| 找bug | ❌错误 | ✅正确 | |
| 代码理解 | ❌失败 | ✅正确 | |
| 数学能力 | 常识问题 | ❌错误 | ✅正确 |
| 年龄问题 | ❌错误 | ✅正确 | |
| 递归问题 | ❌错误 | ✅正确 | |
| 抽象问题 | ❌错误 | ✅正确 | |
| 人格模拟 | 模拟女仆 | ❌失败 | ✅成功 |
看了上表的统计结果,我想文心一言和GPT-4孰强孰弱大家心里一目了然。如果让我给两个模型能力评分的话,我会这么打分:
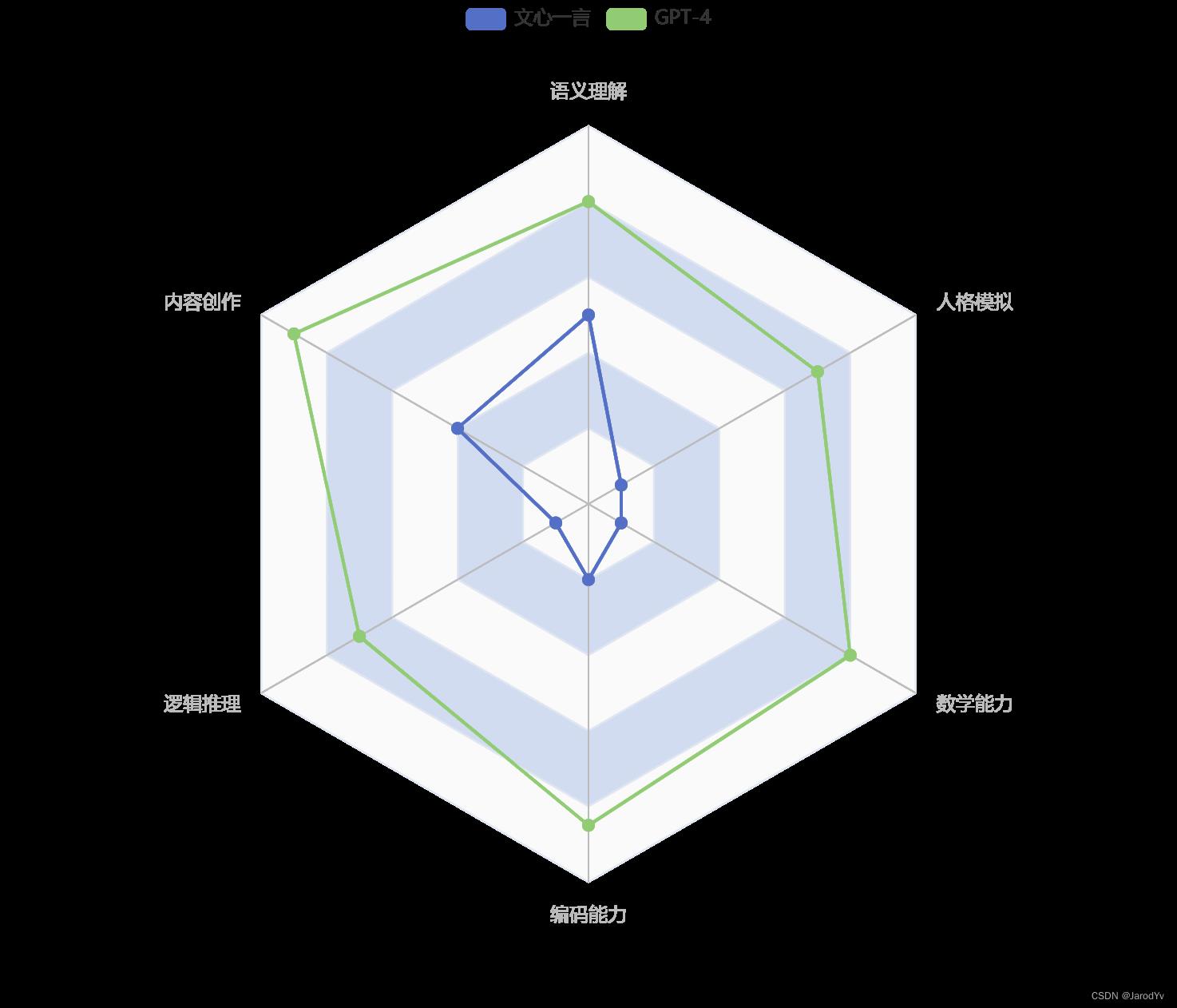
声明:上面评分仅代表我个人,可能存在严重偏见,如有不同意见欢迎留言讨论。
后记
百度文心一言的发布会着实让人失望,因为发布会对于很多关键问题都没有给出明确回答,比如:
- 文心一言用于训练的数据量有多大?数据来源来自哪里?
- 这些数据是如何做标注和对齐的?
- 文心一言的训练方法和架构是什么样的?是跟ChatGPT一样?还是对中文做了改进?
群众的眼睛是雪亮的,文心一言发布会结束后百度股价应声下跌6%。更有网友调侃文心一言的发布会就好像一个退役多年的运动员,突然宣布要代表国家出战奥运会,并且目标是获得奥运会金牌。但整个发布会给我们看了他过往的成绩、看了他先进的训练场地、看了他优秀的教练团队、也摆了几个运动的pose,但就是不说当前的成绩和训练计划。这让我们怎么相信他能够为国去摘金夺银?
我觉得,我们不如大大方方地拿出数据,拿出基准,坦然承认自己比GPT-4还有2年甚至3年的差距,这个态度也许更有助于我们去赶超OpenAI。而不是打肿脸充胖子,不行硬上,最终只会落得自取其辱的下场。
不过话说回来,我认为中国要出一个对标ChatGPT的产品,这个产品只可能来自百度,因为百度拥有训练所需的海量数据,百度百科有大量已经审核和对齐的数据,百度贴吧有大量人工生成的数据,更何况百度可以轻易获得网页数据。接下来唯愿百度不要被商业利益驱使,能沉下心来好好将文心一言打磨好,可以用更开放的姿态吸引更多人才来一起将文心一言打造成可以与ChatGPT竞争的产品。
以上是关于文心一言 VS 讯飞星火 VS chatgpt (22)-- 算法导论4.2 2题的主要内容,如果未能解决你的问题,请参考以下文章