K-Means算法的Python实现

Posted 2021-02-06 camash

算法简介

K-Means是一种常用的聚类算法。聚类在机器学习分类中属于无监督学习，在数据集没有标注的情况下，便于对数据进行分群。而K-Means中的K即指将数据集分成K个子集合。

K-Means演示

从以下的动画、视频和计算过程可以较为直观了解算法的计算过程。

动画展示

视频展示

https://youtu.be/BVFG7fd1H30

在线展示

kmeans测试页面

使用场景

由于简单和低维度下高效的特性，K-Means算法被应用在人群分类，图像分段，文本分类以及数据挖掘前数据预处理场景中。

算法理解

计算流程

一下使用$$分隔的内容为LaTeX编码的数学表达式，请自行解析。
假设有n个点$$x_{1}$$, $$x_{2}$$, $$x_{3}$$, ..., $$x_{n}$$ 以及子集数量K。

• 步骤1 取出K个随机向量作为中心点用于初始化

\\[C = c_{1},c_{2},...,c_{k} \\]

• 步骤2 计算每个点$$x_{n}$$与K个中心点的距离，然后将每个点聚集到与之最近的中心点

\\[\\min_{c_{i} \\in C} dist(c_{i},x) \\]

dist函数用于实现欧式距离计算。

• 步骤3 新的聚集出来之后，计算每个聚集的新中心点

\\[c_{i} = avg(\\sum_{x_{i} \\in S_{i}} x_{i})​ \\]

Si表示归属于第i个中心点的数据。

• 步骤4 迭代步骤2和步骤3，直至满足退出条件（中心点不再变化）

Python代码实现

本代码参考了https://mubaris.com/posts/kmeans-clustering/这篇博客， 用于聚类的数据集可从GitHub上下载到，下载的地址https://github.com/mubaris/friendly-fortnight/blob/master/xclara.csv

Python代码如下：

导包，初始化图形参数，导入样例数据集

%matplotlib inline
from copy import deepcopy
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
plt.rcParams[\'figure.figsize\'] = (16, 9)
plt.style.use(\'ggplot\')


# 导入数据集
data = pd.read_csv(\'xclara.csv\')
# print(data.shape)
# data.head()

将数据集转换为二维数组，并绘制二维坐标图

# 将csv文件中的数据转换为二维数组
f1 = data[\'V1\'].values
f2 = data[\'V2\'].values

X = np.array(list(zip(f1, f2)))
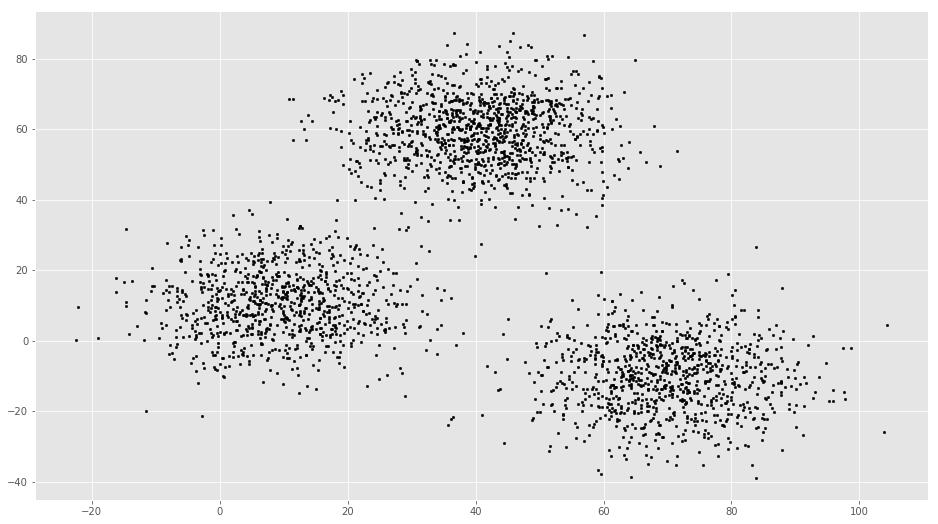
plt.scatter(f1, f2, c=\'black\', s=6)

样例点

定义距离计算函数

# 按行的方式计算两个坐标点之间的距离
def dist(a, b, ax=1):
    return np.linalg.norm(a - b, axis=ax)

初始化分区数，随机获得初始中心点

# 设定分区数
k = 3
# 随机获得中心点的X轴坐标
C_x = np.random.randint(0, np.max(X)-20, size=k)
# 随机获得中心点的Y轴坐标
C_y = np.random.randint(0, np.max(X)-20, size=k)
C = np.array(list(zip(C_x, C_y)), dtype=np.float32)

将初始化中心点和样例数据画到同一个坐标系上

# 将初始化中心点画到输入的样例数据上
plt.scatter(f1, f2, c=\'black\', s=7)
plt.scatter(C_x, C_y, marker=\'*\', s=200, c=\'red\')

初始节点和样例数据节点

实现K-Means中的核心迭代

# 用于保存中心点更新前的坐标
C_old = np.zeros(C.shape)
print(C)
# 用于保存数据所属中心点
clusters = np.zeros(len(X))
# 迭代标识位，通过计算新旧中心点的距离
iteration_flag = dist(C, C_old, 1)

tmp = 1
# 若中心点不再变化或循环次数不超过20次(此限制可取消)，则退出循环
while iteration_flag.any() != 0 and tmp < 20:
    # 循环计算出每个点对应的最近中心点
    for i in range(len(X)):
        # 计算出每个点与中心点的距离
        distances = dist(X[i], C, 1)
        # print(distances)
        # 记录0 - k-1个点中距离近的点
        cluster = np.argmin(distances) 
        # 记录每个样例点与哪个中心点距离最近
        clusters[i] = cluster
        
    # 采用深拷贝将当前的中心点保存下来
    # print("the distinct of clusters: ", set(clusters))
    C_old = deepcopy(C)
    # 从属于中心点放到一个数组中，然后按照列的方向取平均值
    for i in range(k):
        points = [X[j] for j in range(len(X)) if clusters[j] == i]
        # print(points)
        # print(np.mean(points, axis=0))
        C[i] = np.mean(points, axis=0)
        # print(C[i])
    # print(C)
    
    # 计算新旧节点的距离
    print (\'循环第%d次\' % tmp)
    tmp = tmp + 1
    iteration_flag = dist(C, C_old, 1)
    print("新中心点与旧点的距离：", iteration_flag)

将最终结果和样例点画到同一个坐标系上

# 最终结果图示
colors = [\'r\', \'g\', \'b\', \'y\', \'c\', \'m\']
fig, ax = plt.subplots()
# 不同的子集使用不同的颜色
for i in range(k):
        points = np.array([X[j] for j in range(len(X)) if clusters[j] == i])
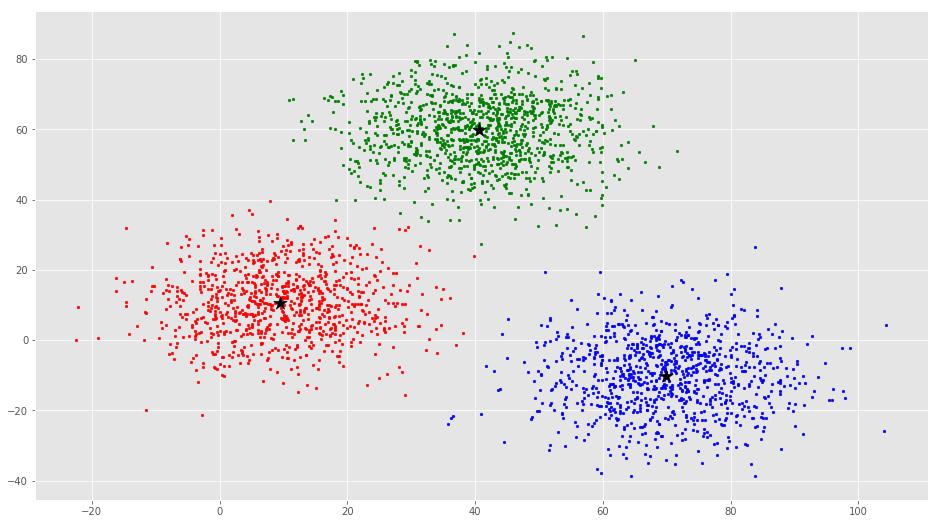
        ax.scatter(points[:, 0], points[:, 1], s=7, c=colors[i])
ax.scatter(C[:, 0], C[:, 1], marker=\'*\', s=200, c=\'black\')

最终计算结果图示