Algorithm_01--C#递归算法02

Posted 2023-05-24 加油啊，敲代码的小伙纸

///递归算法本质：
///1、方法的自我调用
///2、有明确的终止条件
///3、每次调用时，问题规模在不断减少。通过递减，最终到达终止条件

//一列数的规则如下：1、1、2、3、5、8、13、21、34..求第30位数是多少

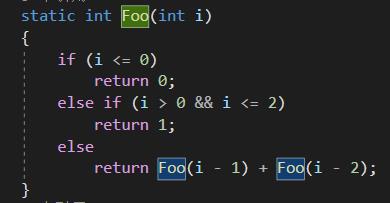
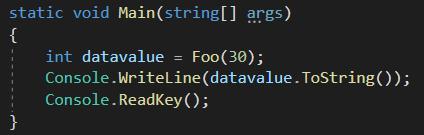
问题：斐波那契数列项数n （即题目所给的数列）

1. 首先判断n=1或2时,直接返回1,这是递归终止条件。
2. 若n>2,则继续递归调用:
   • Fib(n-1) 会一直递归调用直到n=1或2,得到上一项的值
   • Fib(n-2) 同样递归调用直到n=1或2,得到上两项的值
   • 将上一项和上两项相加,得到第n项的值,并返回
3. 所以通过不断递归地求解更小的子问题,最终将达到能直接求解的问题,然后在递归回溯过程中把每个子问题的解累加,得到最终答案。

总结：对于递归，要明确终止条件，然后观察规律。

延申：循环迭代也可以解斐波那契数列

1. 首先判断n=1或2时,直接返回1。这与递归算法相同。
2. 定义3个变量:
   • first 保存上一项的值,初始化为1
   • second 保存上两项的值,初始化为1
   • sum 用来保存计算出的第n项的值
3. 使用for循环,从第3项开始求解: //先定义了一二项，然后通过for循环迭代计算，更新一二项(first second)的值来进行计算
   • 先将上一项和上两项相加,得到第i项的值,赋给sum
   • 然后上一项的值赋给first,上两项的值赋给second
   • 这样在下一轮循环中,first和second就是更新后的上一项和上两项的值
4. 循环执行,直到i=n,此时sum就是第n项的值,返回结果。
5. 与递归算法相比,迭代算法通过定义变量保存每一步的中间结果,从而无需重复运算,效率更高,空间复杂度更小。空间复杂度是用来度量一个算法在运行过程中占用存储空间大小的一个指标。一般来说,空间复杂度小意味着一个算法在运行时占用的存储空间更少。此时,该算法可以被认为在空间利用率上更高效。说人话就是，递归简洁但是占用空间大，循环迭代复杂但是占用空间小。

数据结构&算法_算法基础之前传（递归时间复杂度空间复杂度二分查找）

什么是算法：

　　间而言之算法（Algorithm）：一个计算过程，解决问题的方法

 递归的两个特点：

• 　　调用自身
• 　　结束条件

递归示例：

def func(x):
    if x==0:
        print("我的小鲤鱼",end=\'\')
    else:
        print("抱着",end=\'\')
        func(x-1)
        print("的我",end="")
        
func(5)

递归示例一：我的小鲤鱼

\'\'\'
1 1 2 3 5 8 13 21 34 
输出长度为 n 的斐波那契数列
\'\'\'
#方式一：while 循环
def fibo(num):
    a=1
    b=1
    i=1
    while i<=num:
        print(a,end=" ")
        a,b = b,a+b
        i+=1
# fibo(10)

#方式二：用递归函数方式
#输出某一项
def fibo2(num):
    if num == 1 or num==2:
        return 1
    elif num>2:
        return fibo2(num-1)+fibo2(num-2)
#s输出整个数列
# for i in range(1,11):
#     print(fibo2(i),end=" ")

#方式三
def fibo3(a,b,num):
    if a > num:
        return
    print(a,end=" ")
    fibo3(b,a+b,num)
fibo3(1,1,1100)

递归示例二：斐波那契数列

时间复杂度

 空间复杂度

空间复杂度：用来评估算法内存占用大小的一个式子

利用程序的空间复杂度，可以对程序的运行所需要的内存多少有个预先估计。一个程序执行时除了需要存储空间和存储本身所使用的指令、常数、变量和输入数据外，还需要一些对数据进行操作的工作单元和存储一些为现实计算所需信息的辅助空间。程序执行时所需存储空间包括以下两部分。　　

（1）固定部分。这部分空间的大小与输入/输出的数据的个数多少、数值无关。主要包括指令空间（即代码空间）、数据空间（常量、简单变量）等所占的空间。这部分属于静态空间。

（2）可变空间，这部分空间的主要包括动态分配的空间，以及递归栈所需的空间等。这部分的空间大小与算法有关。

一个算法所需的存储空间用f(n)表示。S(n)=O(f(n))　　其中n为问题的规模，S(n)表示空间复杂度。

 

二分查找

思路：

从有序列表的候选区data[0:n]开始，通过对待查找的值与候选区中间值的比较，可以使候选区减少一半。

 特点：

二分查找适合有序列表
时间复杂度 O(logn)

 

#!/usr/bin/env python
# -*- coding:utf-8 -*-
\'\'\'
二分查找适合有序列表
时间复杂度 O(logn)
\'\'\'
def bin_search(li,val):
    low = 0
    high = len(li) -1
    while li[low] <= li[high]:
        mid = (low+high)//2
        if li[mid] == val:
            print("search success! the index is:{0}".format(mid))
            return None
        elif li[mid] < val :
            low = mid+1
        else:
            high = mid -1
    else:
        print("val is not exist")
        return None

# 二分查找递归版：
def bin_search_rec(li,val,low,high):
    mid = (low+high)//2
    while li[low] <= li[high]:
        if li[mid] == val:
            print("search success! the index is:{0}".format(mid))
            return None
        elif li[mid] < val:
            return bin_search_rec(li, val, mid+1, high)
        else:
            return bin_search_rec(li, val, low, mid-1)
    else:
        print("val is not exist")
        return None
li = [1,3,6,8,9,11,14,16,22,31,44,56,58]
bin_search_rec(li,23,0,12)