代码随想录算法训练营第14天 | ● 理论基础 ● 递归遍历 ● 迭代遍历 ● 统一迭代

Posted 2023-05-23 小懒懒

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了代码随想录算法训练营第14天 | ● 理论基础 ● 递归遍历 ● 迭代遍历 ● 统一迭代相关的知识，希望对你有一定的参考价值。

第六章二叉树part01

今日内容：

● 理论基础

● 递归遍历

● 迭代遍历

● 统一迭代

详细布置

理论基础

需要了解二叉树的种类，存储方式，遍历方式以及二叉树的定义

文章讲解：https://programmercarl.com/%E4%BA%8C%E5%8F%89%E6%A0%91%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html

递归遍历（必须掌握）

二叉树的三种递归遍历掌握其规律后，其实很简单

题目链接/文章讲解/视频讲解：https://programmercarl.com/%E4%BA%8C%E5%8F%89%E6%A0%91%E7%9A%84%E9%80%92%E5%BD%92%E9%81%8D%E5%8E%86.html

迭代遍历（基础不好的录友，迭代法可以放过）

题目链接/文章讲解/视频讲解：https://programmercarl.com/%E4%BA%8C%E5%8F%89%E6%A0%91%E7%9A%84%E8%BF%AD%E4%BB%A3%E9%81%8D%E5%8E%86.html

统一迭代（基础不好的录友，迭代法可以放过）

这是统一迭代法的写法，如果学有余力，可以掌握一下

题目链接/文章讲解：https://programmercarl.com/%E4%BA%8C%E5%8F%89%E6%A0%91%E7%9A%84%E7%BB%9F%E4%B8%80%E8%BF%AD%E4%BB%A3%E6%B3%95.html

往日任务

● day 1 任务以及具体安排：训练营一期day 1

● day 2 任务以及具体安排：day 2 第一章数组

● day 3 任务以及具体安排：day 3 第二章链表

● day 4 任务以及具体安排：day 4 第二章链表

● day 5 周日休息

● day 6 任务以及具体安排：day 6 第三章哈希表

● day 7 任务以及具体安排：day 7 第三章哈希表

● day 8 任务以及具体安排：day 8 第四章字符串

● day 9 任务以及具体安排：day 9 第四章字符串

● day 10 任务以及具体安排：day 10 第四章字符串

● day 11 任务以及具体安排：day 11 第五章栈与队列

● day 12 周日休息

● day 13 任务以及具体安排：day 13 第五章栈与队列

代码随想录算法训练营第三十八天 | 理论基础，509. 斐波那契数，70. 爬楼梯，746. 使用最小花费爬楼梯

Day36 周日休息~

一、参考资料

理论基础

https://programmercarl.com/%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html

刷题大纲

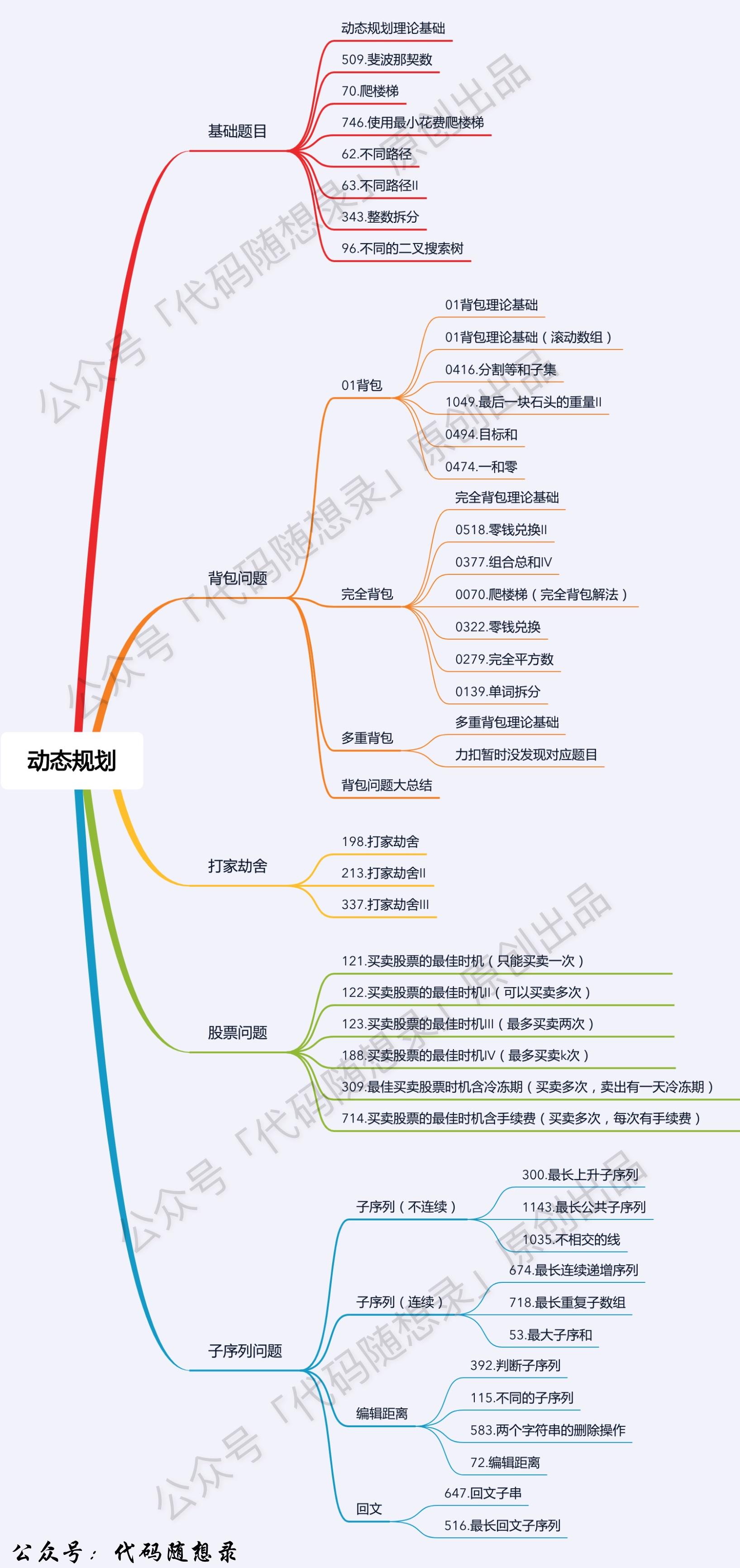
递推五部曲：

确定dp数组（dp table）以及下标的含义

确定递推公式

dp数组如何初始化

确定遍历顺序

举例推导dp数组

斐波那契数（通常用 F(n) 表示）形成的序列称为斐波那契数列。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：
F(0) = 0，F(1) = 1 F(n) = F(n - 1) + F(n - 2)，其中 n > 1
给定 n ，请计算 F(n) 。

示例 1：
输入：n = 2 输出：1 解释：F(2) = F(1) + F(0) = 1 + 0 = 1
示例 2：
输入：n = 3 输出：2 解释：F(3) = F(2) + F(1) = 1 + 1 = 2
示例 3：
输入：n = 4 输出：3 解释：F(4) = F(3) + F(2) = 2 + 1 = 3
提示：
0 <= n <= 30


class Solution 
public:
    int fib(int n) 
        if (n <= 1) return n;
        vector<int> dp(n + 1);
        dp[0] = 0;
        dp[1] = 1;
        for (int i = 2; i <= n; i++) 
            dp[i] = dp[i - 1] + dp[i - 2];
        
        return dp[n];
    
;

进一步优化：


class Solution 
public:
    // 两个值维护即可
    int fib(int n) 
        if (n <= 1) return n;
        int dp[2];
        dp[0] = 0;
        dp[1] = 1;
        for (int i = 2; i <= n; i++) 
            int res = dp[0] + dp[1];
            dp[0] = dp[1];
            dp[1] = res;
        
        return dp[1];
    
;

三、LeetCode70. 爬楼梯

https://leetcode.cn/problems/climbing-stairs/description/

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例 1：
输入：n = 2 输出：2 解释：有两种方法可以爬到楼顶。 1. 1 阶 + 1 阶 2. 2 阶
示例 2：
输入：n = 3 输出：3 解释：有三种方法可以爬到楼顶。 1. 1 阶 + 1 阶 + 1 阶 2. 1 阶 + 2 阶 3. 2 阶 + 1 阶
提示：
1 <= n <= 45

举例：


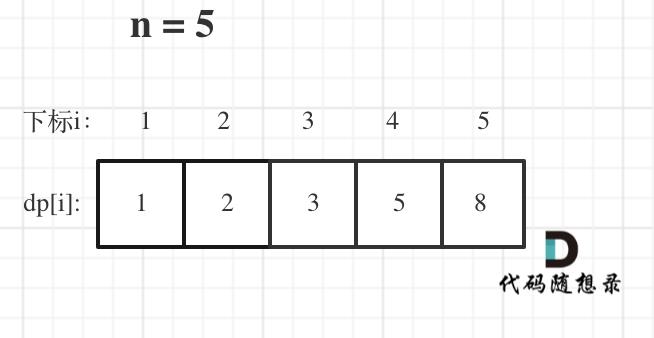
class Solution 
public:
    int climbStairs(int n) 
        if (n <= 1) return n;
        vector<int> dp(n + 1);
        dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i <= n; i++) 
            dp[i] = dp[i - 1] + dp[i - 2];
        
        return dp[n];
    
;

四、LeetCode746. 使用最小花费爬楼梯

https://leetcode.cn/problems/min-cost-climbing-stairs/description/

给你一个整数数组 cost ，其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用，即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。

示例 1：
输入：cost = [10, 15,20] 输出：15 解释：你将从下标为 1 的台阶开始。 - 支付 15 ，向上爬两个台阶，到达楼梯顶部。总花费为 15 。
示例 2：
输入：cost = [ 1,100, 1,1, 1,100, 1, 1,100, 1] 输出：6 解释：你将从下标为 0 的台阶开始。 - 支付 1 ，向上爬两个台阶，到达下标为 2 的台阶。 - 支付 1 ，向上爬两个台阶，到达下标为 4 的台阶。 - 支付 1 ，向上爬两个台阶，到达下标为 6 的台阶。 - 支付 1 ，向上爬一个台阶，到达下标为 7 的台阶。 - 支付 1 ，向上爬两个台阶，到达下标为 9 的台阶。 - 支付 1 ，向上爬一个台阶，到达楼梯顶部。总花费为 6 。
提示：
2 <= cost.length <= 1000
0 <= cost[i] <= 999

举例：


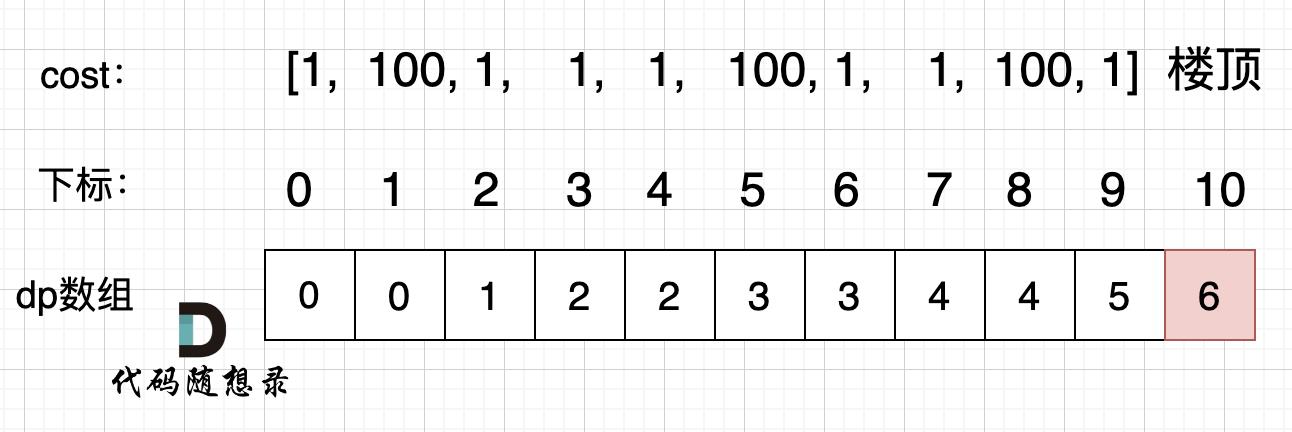
class Solution 
public:
    int minCostClimbingStairs(vector<int>& cost) 
        vector<int> dp(cost.size() + 1);
        dp[0] = 0;
        dp[1] = 0;
        for (int i = 2; i <= cost.size(); i++) 
            dp[i] = min(dp[i - 2] + cost[i - 2], dp[i - 1] + cost[i - 1]);
        
        return dp[cost.size()];
    
;