AcWing905.区间选点

Posted 2023-05-22 JaineCC

题目详情

知识点

区间贪心
为什么叫贪心呢？

——短视，每次只是在看眼前的东西，在眼前的决策中选一个最优解。而贪心就是根据这种策略能够走到全局最优解的方法【如果用函数图像来表示就是一个单峰的图】

贪心的普遍方案

一般来说贪心问题没有思路的时候我们可以先随便试一下，再去举一些例子看自己的方法有什么缺漏，如果没什么问题的话就去证明一下这个方法的有效性

思路

自己的思路：（错误的仅供参考）

对于这种题不知道为什么总是下意识想按照左端点排序，然后再一个个判定，但是这样会忽略一种情况

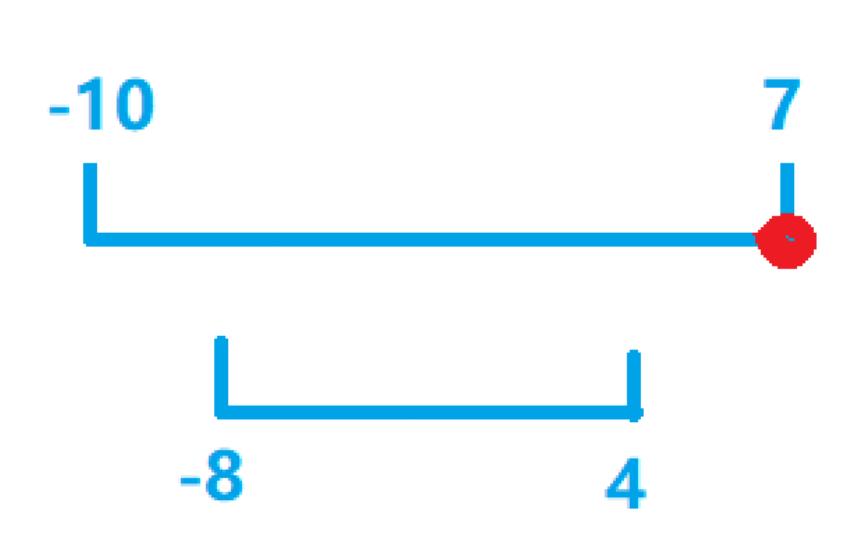
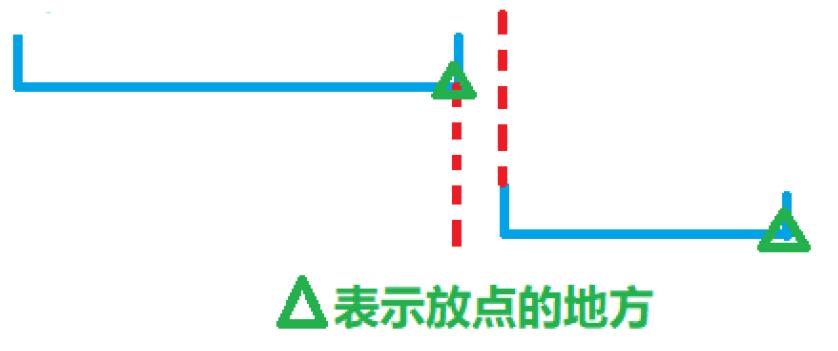
对于上图这种情况，我会默认放在较大区间的右端点处，但是这种情况对于区间[-8,4]里面是没有点的！

n = int(input())
arr = []
for i in range(n):
    l,r = map(int,input().split())
    arr.append([l,r])
arr.sort(key=lambda x:x[0])
res = 1
l = arr[0][1]
print(l)
for i in range(1,n):
    if arr[i][0] > l:
        res += 1
    l = max(l,arr[i][1])
print(res)

正确的思路

区间贪心问题的分析：无外乎就是排序（按左端点or右端点or双关键字）

先试想一个方法：

• 将每个区间按右端点从小到大排序
• 从前往后依次枚举每个区间
  • 如果当前区间中已经包含点，则直接pass
  • 否则，选择当前区间的右端点

好的，我们现在找到了一个算法，现在我们得证明该算法的有效性

我们可以利用数学中的证明方法：要证明A=B

就要证明①A≥B；②A≤B。我们遵循这个思路进行证明

用ans表示最终答案，用cnt表示通过该算法求出的答案

首先每个区间一定都包含一个点，因此当前选点方案肯定是一组合法方案

本题的最优解指的是：所有合法方案中的最小值，所以有①ans≤cnt

对于算法第二步的第二种情况，对所有没被pass的情况

第一个区间肯定被选了，那下一个被选的点肯定是与当前这个区间没有任何交点的区间，如下图所示

然后我们依次找到了cnt个点，对应cnt个区间，是从左到右互不相交的区间

所以如果要覆盖这些区间，那至少要用cnt个点，而题目要求我们所选的点要覆盖所有区间（一定包括这些互不相交的区间）

所以可选方案一定要包括这些点②ans≥cnt

因此，ans=cnt，方法可行

代码

n = int(input())
arr = []
for i in range(n):
    l,r = map(int,input().split())
    arr.append([l,r])
arr.sort(key=lambda x:x[1])
res = 1
r = arr[0][1]
for i in range(1,n):
    if arr[i][0] > r:
        res += 1  # 放一个点
        r = arr[i][1] # 放在右端点
print(res)

自己思路的优化

以上是比较好理解的思路，但其实用左端点排序（就是我自己的思路的方法）也可以，但是在更新的过程中要取最小值。
因为左端点排序的话，一个大区间会存在多个小区间；那么要想点数尽可能少，那么就选择小区间的右端点作为覆盖点，小区间可以覆盖大区间，但是不能覆盖大区间内另一个没有重复区域的小区间，所以要维护最右端点值

n = int(input())
arr = []
for i in range(n):
    l,r = map(int,input().split())
    arr.append([l,r])
arr.sort(key=lambda x:x[0])
res = 1
r = arr[0][1]
for i in range(1,n):
    if arr[i][0] > r:
        res += 1
        r = arr[i][1]
    else:
        r = min(r,arr[i][1])
print(res)

AcWing 905. 区间选点 贪心

题
参考

排序要排右端点。

#include<bits/stdc++.h>
using namespace std;
#define fir(i,a,n) for(int i=a;i<=n;i++)
//======================
const int N=1e5+10;
struct node
{
	int a,b;
}a[N];
int n;
bool cmp(node a,node b)
{
	return a.b<b.b;
}
int main()
{
	cin>>n;
	fir(i,1,n) 
	{
		int aa,bb;cin>>aa>>bb;
		a[i]={aa,bb};
	}
	sort(a+1,a+1+n,cmp);
	int ans=1;
	int now=a[1].b;
	for(int i=2;i<=n;i++)
	{
		//cout<<now<<" "<<a[i].b<<endl;
		if(now<a[i].a)
		{
			now=a[i].b;ans++;
		}
	}
	cout<<ans;
	return 0; 
}