AtCoder Regular Contest 130 C Digit Sum Minimization
Posted zltzlt
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了AtCoder Regular Contest 130 C Digit Sum Minimization相关的知识,希望对你有一定的参考价值。
分类讨论,但是写起来挺答辩的。
首先发现我们要使进位尽量多。
特判怎么重排都没有进位的情况(\\(a_i + b_i < 10\\))。然后枚举个位选的两个数字,并且要求它们和 \\(\\ge 10\\)。
- 如果当前位两个位都有数字,那么从小到大枚举数位的和 \\(\\in [9, 18]\\);如果有数字加起来等于枚举的和就直接进入下一位。注意要优先选非 \\(9\\) 的数,这样留给后面只有一位有数字的进位就更多。如果当前位不可能产生进位了,那么就直接摆烂,随便选。
- 如果当前位只有一位有数字,优先选 \\(9\\),然后再选其他的(其实不需要)。
然后就做完了。
code
// Problem: C - Digit Sum Minimization
// Contest: AtCoder - AtCoder Regular Contest 130
// URL: https://atcoder.jp/contests/arc130/tasks/arc130_c
// Memory Limit: 1024 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include <bits/stdc++.h>
#define pb emplace_back
#define fst first
#define scd second
#define mems(a, x) memset((a), (x), sizeof(a))
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef double db;
typedef long double ldb;
typedef pair<ll, ll> pii;
const int maxn = 100100;
int n, m, ca[15], cb[15], cc[15], cd[15];
char a[maxn], b[maxn], c[maxn], s[maxn], t[maxn], ss[maxn], tt[maxn];
void solve()
scanf("%s%s", a + 1, b + 1);
n = strlen(a + 1);
m = strlen(b + 1);
bool flag = 0;
if (n < m)
swap(n, m);
swap(a, b);
flag = 1;
if (m < n)
for (int i = 1; i <= n - m; ++i)
c[i] = \'0\';
for (int i = n - m + 1, j = 1; i <= n; ++i)
c[i] = b[j++];
for (int i = 1; i <= n; ++i)
b[i] = c[i];
// printf("%s %s\\n", a + 1, b + 1);
for (int i = 1; i <= n; ++i)
++ca[a[i] - \'0\'];
for (int i = 1; i <= n; ++i)
++cb[b[i] - \'0\'];
bool flg = 1;
for (int i = 1; i <= 9; ++i)
for (int j = 1; j <= 9; ++j)
if (i + j >= 10 && ca[i] && cb[j])
flg = 0;
break;
if (!flg)
break;
if (flg)
memcpy(ss, a, sizeof(a));
memcpy(tt, b, sizeof(b));
if (flag)
for (int i = n - m + 1; i <= n; ++i)
putchar(tt[i]);
putchar(\'\\n\');
for (int i = 1; i <= n; ++i)
putchar(ss[i]);
else
for (int i = 1; i <= n; ++i)
putchar(ss[i]);
putchar(\'\\n\');
for (int i = n - m + 1; i <= n; ++i)
putchar(tt[i]);
return;
for (int i = 0; i <= 10; ++i)
cc[i] = ca[i];
cd[i] = cb[i];
int mxk = -1;
for (s[n] = \'1\'; s[n] <= \'9\'; ++s[n])
for (t[n] = \'1\'; t[n] <= \'9\'; ++t[n])
for (int i = 0; i <= 10; ++i)
ca[i] = cc[i];
cb[i] = cd[i];
if (!ca[s[n] - \'0\'] || !cb[t[n] - \'0\'])
continue;
--ca[s[n] - \'0\'];
--cb[t[n] - \'0\'];
int xx = s[n] - \'0\', yy = t[n] - \'0\';
if (xx + yy < 10)
continue;
int k = 1;
for (int i = n - 1; i; --i)
if (b[i] == \'0\')
if (ca[9])
--ca[9];
s[i] = \'9\';
++k;
else
for (int x = 1; x <= 9; ++x)
if (ca[x])
--ca[x];
s[i] = \'0\' + x;
break;
continue;
bool fl = 0;
for (int o = 9; o <= 18; ++o)
for (int p = 1; p < o; ++p)
int q = o - p;
if (1 <= p && p < 9 && 1 <= q && q < 9)
if (ca[p] && cb[q])
s[i] = \'0\' + p;
t[i] = \'0\' + q;
--ca[p];
--cb[q];
fl = 1;
break;
else if (cb[p] && ca[q])
--cb[p];
--ca[q];
s[i] = \'0\' + q;
t[i] = \'0\' + p;
fl = 1;
break;
if (fl)
++k;
break;
for (int p = 1; p < o; ++p)
int q = o - p;
if ((p == 9 && 1 <= q && q <= 9) || (q == 9 && 1 <= p && p <= 9))
if (ca[p] && cb[q])
s[i] = \'0\' + p;
t[i] = \'0\' + q;
--ca[p];
--cb[q];
fl = 1;
break;
else if (cb[p] && ca[q])
--cb[p];
--ca[q];
s[i] = \'0\' + q;
t[i] = \'0\' + p;
fl = 1;
break;
if (fl)
++k;
break;
if (!fl)
for (int o = 2; o < 9; ++o)
for (int p = 1; p < o; ++p)
int q = o - p;
if (1 <= p && p <= 9 && 1 <= q && q <= 9)
if (ca[p] && cb[q])
s[i] = \'0\' + p;
t[i] = \'0\' + q;
--ca[p];
--cb[q];
fl = 1;
break;
else if (cb[p] && ca[q])
--cb[p];
--ca[q];
s[i] = \'0\' + q;
t[i] = \'0\' + p;
fl = 1;
break;
if (fl)
break;
if (k > mxk)
mxk = k;
memcpy(ss, s, sizeof(s));
memcpy(tt, t, sizeof(t));
if (flag)
for (int i = n - m + 1; i <= n; ++i)
putchar(tt[i]);
putchar(\'\\n\');
for (int i = 1; i <= n; ++i)
putchar(ss[i]);
else
for (int i = 1; i <= n; ++i)
putchar(ss[i]);
putchar(\'\\n\');
for (int i = n - m + 1; i <= n; ++i)
putchar(tt[i]);
int main()
int T = 1;
// scanf("%d", &T);
while (T--)
solve();
return 0;
Donation---AtCoder - AtCoder Regular Contest 098
Donation
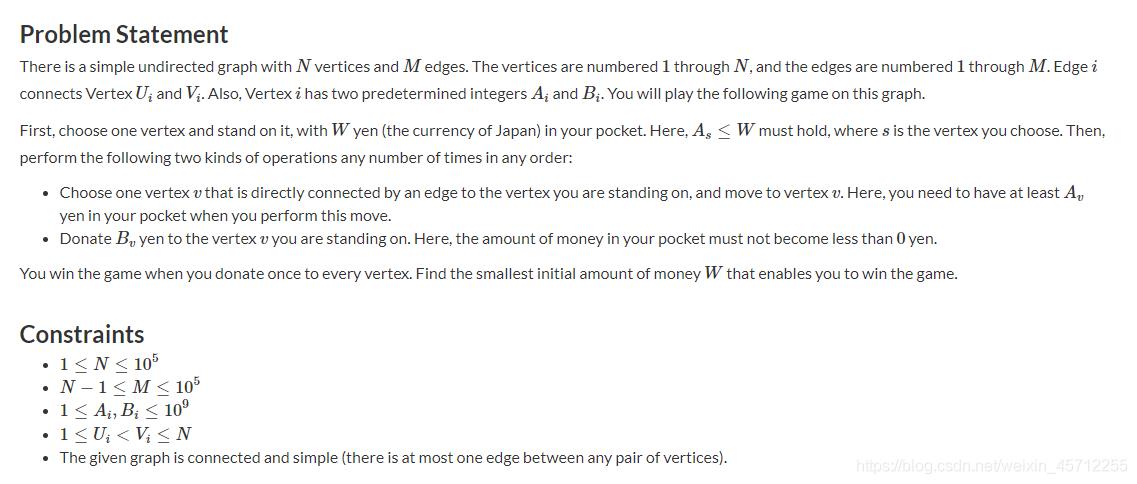
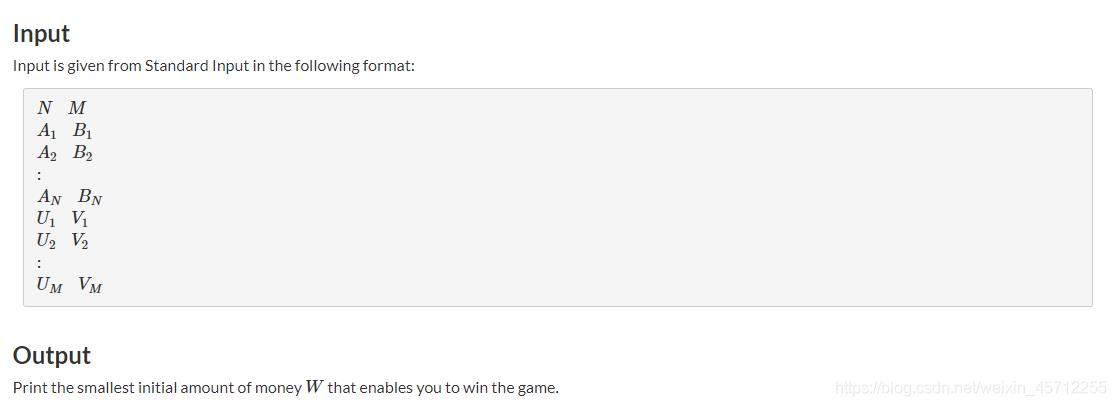
input1:
4 5
3 1
1 2
4 1
6 2
1 2
2 3
2 4
1 4
3 4
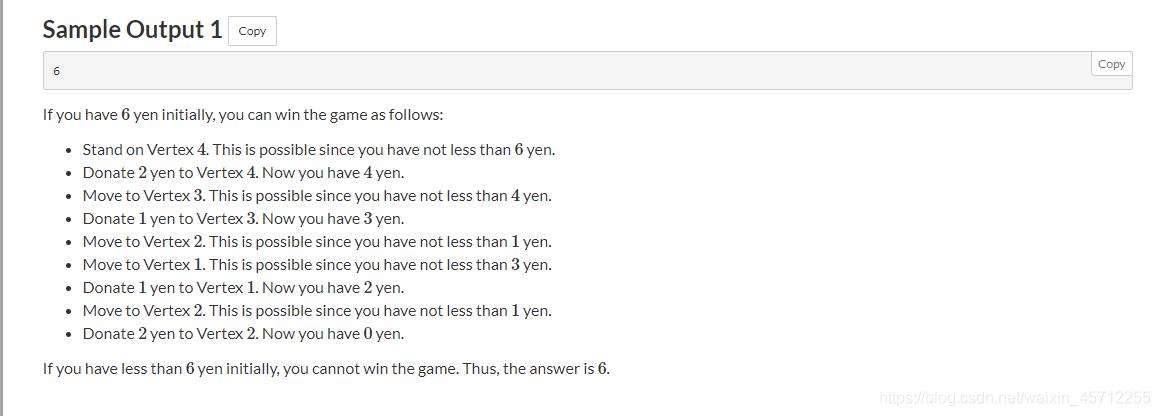
input2:
5 8
6 4
15 13
15 19
15 1
20 7
1 3
1 4
1 5
2 3
2 4
2 5
3 5
4 5
output2:
44
input3:
9 10
131 2
98 79
242 32
231 38
382 82
224 22
140 88
209 70
164 64
6 8
1 6
1 4
1 3
4 7
4 9
3 7
3 9
5 9
2 5
output3:
582
有n个点m条边,每一个点有两个属性,在这个点上的时候要至少有A元,然后要在这个点上支付B元,可以选择在任意时候支付
求最少要携带多少元,才能够将所有的点都支付一遍
int head[maxn];
int n,m,cnt,tot;
ll a[maxn],b[maxn],c[maxn],id[maxn];
int fa[maxn];
int lson[maxn],rson[maxn];
struct node{
int v,nex;
}e[maxn];
void addEdge(int u,int v){
e[cnt].v = v;
e[cnt].nex = head[u];
head[u] = cnt ++;
}
void init(){
for(int i=0;i<maxn;i++) fa[i] = i,head[i] = -1;
cnt = 0;
tot = 0;
}
bool cmp(int x,int y){
return a[x] < a[y];
}
int find(int x){
if(x == fa[x]) return x;
else return fa[x] = find(fa[x]);
}
void add(int u,int v){
int fau = find(u);
int fav = find(v);
if(fau == fav) return ;
tot ++;
u = fau;
v = fav;
lson[tot] = u;
rson[tot] = v;
a[tot] = max(a[u],a[v]);
b[tot] = b[u] + b[v];///cost cal
fa[u] = tot;
fa[v] = tot;
fa[tot] = tot;
}
ll dp[maxn];
void dfs(int u){
if(lson[u]){
dfs(lson[u]);
dfs(rson[u]);
}else dp[u] = a[u];
dp[u] = min(
max(a[u]-b[lson[u]],dp[lson[u]]),
max(a[u]-b[rson[u]],dp[rson[u]])
);
}
int main()
{
init();
n = read,m = read;
for(int i=1;i<=n;i++) a[i] = read,b[i] = read;
for(int i=1;i<=n;i++) a[i] = max(a[i] - b[i], 0LL),id[i] = i;
sort(id+1,id+1+n,cmp);
for(int i=1;i<=m;i++){
int u = read,v = read;
addEdge(u,v);
addEdge(v,u);
}
/*for(int i=1;i<=n;i++){
cout<<id[i]<<' ';
}
puts("");*/
tot = n;
// puts("ok");
for(int i=1;i<=n;i++){
int u = id[i];
for(int j = head[u]; ~j; j = e[j].nex){
int to = e[j].v;
if(a[to] <= a[u]) add(u,to);
}
}
dfs(tot);
cout << dp[tot] + b[tot] <<endl;
return 0;
}
以上是关于AtCoder Regular Contest 130 C Digit Sum Minimization的主要内容,如果未能解决你的问题,请参考以下文章