AC自动机
Posted wonder-land
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了AC自动机相关的知识,希望对你有一定的参考价值。
前言
在学习AC自动机前,请确保已经学习并能熟练运用:
-
KMP匹配
-
字典树
引入
在漫长的OI路途,我们难免要接触到一种叫字符串的东西。
在解决关于字符串的问题时,我们又难免要解决两个字符串匹配的问题,
比如,在一个字符串s中,字符串t出现了多少次 这些问题。(详见KMP匹配)
而在OI路途也不是一直可以一帆风顺的,万恶的出题人绝对不会总让你只匹配一个字符串,他们肯定要想方设法提高些难度,比如一个文本串匹配多个匹配串……
显然,这时候我们不可能对着那么多个字符串一个一个的做KMP,这时候就要用到本文的内容:AC自动机。
AC自动机
AC自动机是建立在字典树和KMP思想上的产物,从某种意义上来说,KMP匹配也是AC自动机的一种特殊情况(字典树只有一条链的时候)。
它通过建立所有匹配串的字典树,在每个节点建立失配指针fail来将各节点联系起来。
指针fail指向的是当前串最长后缀的节点,这样可以保证沿着fail一直跳下去,不会漏掉任何一个后缀节点。
在文本串匹配时,对于文本串的每一个前缀串,通过跳fail指针将其后缀串全部搜一遍,累加答案即可。
P3808 【模板】AC 自动机(简单版)
code:
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+5,maxs=1e6+5;
int n,f[maxs][27],root=0,cnt=0;
int add[maxs],fail[maxs];
string s;
void insert(string s)
int now=root;
for(int i=0;i<s.size();i++)
int c=s[i]-\'a\';
if(!f[now][c]) f[now][c]=++cnt;
now=f[now][c];
add[now]++;
return ;
void build()
queue<int>q;
for(int i=0;i<26;i++)
if(f[root][i]) q.push(f[root][i]);
while(!q.empty())
int now=q.front();
q.pop();
for(int i=0;i<26;i++)
if(f[now][i])
fail[f[now][i]]=f[fail[now]][i];
q.push(f[now][i]);
else f[now][i]=f[fail[now]][i];
return ;
int query(string s)
int now=root,re=0;
for(int i=0;i<s.size();i++)
now=f[now][s[i]-\'a\'];
for(int j=now;j&&add[j]!=-1;j=fail[j])
re+=add[j],add[j]=-1;
return re;
int main()
cin>>n;
for(int i=1;i<=n;i++)
cin>>s;
insert(s);
build();
cin>>s;
cout<<query(s);
return 0;
P5357 【模板】AC 自动机(二次加强版)
code:
#include<bits/stdc++.h>
using namespace std;
const int maxn=2e5+5,maxs=2e5+5;
int n,ch[maxs][26],cnt=0,root=0,num[maxs],fail[maxs],idx[maxn];
string s[maxn],t;
vector<int>edge[maxs];
void insert(string s,int id)
int now=root;
for(int i=0;i<s.size();i++)
int c=s[i]-\'a\';
if(!ch[now][c]) ch[now][c]=++cnt;
now=ch[now][c];
idx[id]=now;
return ;
void build()
queue<int>q;
for(int i=0;i<26;i++)
if(ch[root][i]) q.push(ch[root][i]),edge[root].push_back(ch[root][i]);
while(!q.empty())
int now=q.front();
q.pop();
for(int i=0;i<26;i++)
if(ch[now][i])
fail[ch[now][i]]=ch[fail[now]][i];
edge[ch[fail[now]][i]].push_back(ch[now][i]);
q.push(ch[now][i]);
else ch[now][i]=ch[fail[now]][i];
return ;
void query(string s)
int now=root;
for(int i=0;i<s.size();i++)
int c=s[i]-\'a\';
now=ch[now][c];
num[now]++;
return ;
void dfs(int now)
for(int i=0;i<edge[now].size();i++)
dfs(edge[now][i]),num[now]+=num[edge[now][i]];
return ;
int main()
cin>>n;
for(int i=1;i<=n;i++)
cin>>s[i],insert(s[i],i);
build();
cin>>t;
query(t);
dfs(root);
for(int i=1;i<=n;i++)
cout<<num[idx[i]]<<endl;
return 0;
AC 自动机
AC 自动机
1 算法简介
AC 自动机是一个以 Trie 为基础结合 KMP 的思想建立的。在 AC 自动机中,每一个状态代表着某个模式串的前缀,而整个 DFA 的结构其实是所有模式串的 Trie 树。
而 AC 自动机可以处理这样一个问题:多模式匹配。即给你若干个模式串和一个主串,要求我们对每一个字符串和主串进行匹配。
我们肯定不能做多次 KMP,所以我们有了 AC 自动机。
2 算法讲解
2.1 状态设计
struct node{
int ch[26],end,fail;
};
其中,ch 数组是 Trie 树的指针,end 是判断这个状态为多少串的节点,fail 指针是后缀链接,指向具有相同后缀的状态。比如这个动图(其中的黄线是后缀链接):
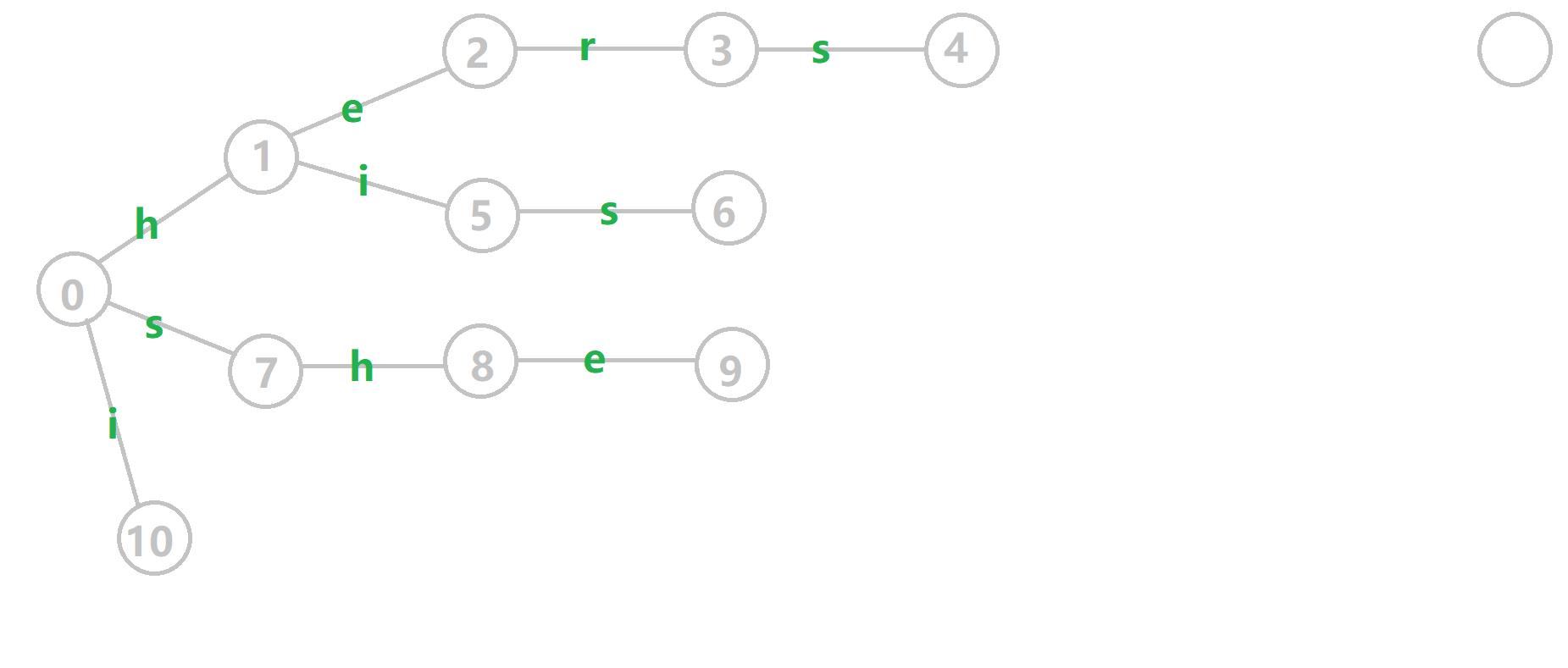
其中 \\(2\\) 节点的指针画错了,应该是指向 \\(0\\)。
2.2 插入
因为自身结构就是 Trie 的结构,所以 AC 自动机的插入和 Trie 树的插入是一模一样的。
代码:
inline void insert(char *s){
int now=0,len=strlen(s);
for(int i=0;i<len;i++){
int k=s[i]-\'a\';
if(!p[now].ch[k]) p[now].ch[k]=++tot;
now=p[now].ch[k];
}
p[now].end++;
}
2.3 建立
在这里,我们需要建立 AC 自动机,Trie 树已经建好了,我们的目的是构建失配指针 fail 。暴力构建的话就是取其父节点,然后不断跳 fail ,直到调到一个状态,它有一条有相同字符的出边。但是这样时间复杂度不优,怎样优化?
我们先上代码:
inline void build(){
queue<int> q;
for(int i=0;i<26;i++) if(p[0].ch[i]) q.push(p[0].ch[i]);
while(q.size()){
int top=q.front();q.pop();
for(int i=0;i<26;i++){
if(p[top].ch[i]) p[p[top].ch[i]].fail=p[p[top].fail].ch[i],q.push(p[top].ch[i]);
else p[top].ch[i]=p[p[top].fail].ch[i];
}
}
}
这里我们通过对跳 fail 的路径进行压缩,如果子节点存在,那就好说,我们把 fail 直接连过来就可以,但是如果不存在,我们就采用路径压缩,把其 fail 的子节点连过来,这样就完成了路径压缩。
放图:

2.4 查询
我们接下来分析查询函数 query ,这个函数将实现多模式匹配。我们直接放代码:
inline int query(char *t){
int now=0,res=0,len=strlen(t);
for(int i=0;i<len;i++){
now=p[now].ch[t[i]-\'a\'];
for(int j=now;j&&~p[j].end;j=p[j].fail) res+=p[j].end,p[j].end=-1;
}
return res;
}
什么意思?注意到我们对于 \\(t\\) 的每一个前缀,查询一下能匹配这个前缀的字符串,方法就是我们在 Trie 上走,然后对于每一个状态跳后缀链接,累加所有是结束节点的地方,注意因为可能重复调到同一个节点,所以我们要对所有的节点进行标记,这里 ~(-1)=0 ,这是一个很妙的打标记方式。
如果 Trie 树走到头了,会回到 \\(0\\) 号节点
2.5 时间复杂度分析
设所有模式串的总长为 \\(N\\),主串的长度为 \\(m\\) ,那么建立 Trie 树的复杂度为 \\(O(N)\\),查询时最坏情况是所有的后缀链接都被便利,为 \\(O(N)\\) ,再加上主串走 Trie 树,复杂度为 \\(O(m)\\)。
所以总复杂度为 \\(O(N+m)\\)
2.6 总代码
#include<bits/stdc++.h>
#define dd double
#define ld long double
#define ll long long
#define uint unsigned int
#define ull unsigned long long
#define N 1000010
#define M number
using namespace std;
const int INF=0x3f3f3f3f;
template<typename T> inline void read(T &x) {
x=0; int f=1;
char c=getchar();
for(;!isdigit(c);c=getchar()) if(c == \'-\') f=-f;
for(;isdigit(c);c=getchar()) x=x*10+c-\'0\';
x*=f;
}
struct node{
int ch[26],cnt,end,fail;
};
struct AC_automaton{
node p[N];int tot;
inline AC_automaton(){tot=0;}
inline void insert(char *s){
int now=0,len=strlen(s);
for(int i=0;i<len;i++){
int k=s[i]-\'a\';
if(!p[now].ch[k]) p[now].ch[k]=++tot;
now=p[now].ch[k];
}
p[now].end++;
}
inline void build(){
queue<int> q;
for(int i=0;i<26;i++) if(p[0].ch[i]) q.push(p[0].ch[i]);
while(q.size()){
int top=q.front();q.pop();
for(int i=0;i<26;i++){
if(p[top].ch[i]) p[p[top].ch[i]].fail=p[p[top].fail].ch[i],q.push(p[top].ch[i]);
else p[top].ch[i]=p[p[top].fail].ch[i];
}
}
}
inline int query(char *t){
int now=0,res=0,len=strlen(t);
for(int i=0;i<len;i++){
now=p[now].ch[t[i]-\'a\'];
for(int j=now;j&&~p[j].end;j=p[j].fail) res+=p[j].end,p[j].end=-1;
}
return res;
}
};
AC_automaton ac;
int n;
char s[N],t[N];
int main(){
read(n);
for(int i=1;i<=n;i++) scanf("%s",s),ac.insert(s);
scanf("%s",t);
ac.build();printf("%d",ac.query(t));
return 0;
}
2.7 加强版
洛谷上有两次 AC 自动机加强版,分别是:
对于例题 1,你只要把每个字符串出现的次数记下来排序就可以了,代码如下(码风略有点不同),注意 \\(end\\) 的含义稍微有点变化。
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<sstream>
#include<queue>
#include<map>
#include<vector>
#include<set>
#include<deque>
#include<cstdlib>
#include<ctime>
#define dd double
#define ld long double
#define ll long long
#define ull unsigned long long
#define N 160
#define M 10001000
using namespace std;
const int INF=0x3f3f3f3f;
inline int read(){
int x=0,f=1;
char ch=getchar();
while(ch<\'0\'||ch>\'9\'){if(ch==\'-\')f=-1;ch=getchar();}
while(ch>=\'0\'&&ch<=\'9\'){x=x*10+ch-\'0\';ch=getchar();}
return x*f;
}
struct rode{
int id,sum;
char s[N];
inline bool operator < (const rode b){
if(sum!=b.sum) return sum>b.sum;
return id<b.id;
}
};
rode a[N];
char t[M];
struct ACzdj{
int tr[N*100][26],cnt;
int end[N*100];int fail[N*100];
inline void insert(char *s,int id){
int p=0;
for(int i=0;s[i];i++){
int k=s[i]-\'a\';
if(!tr[p][k]) tr[p][k]=++cnt;
p=tr[p][k];
}
end[p]=id;
}
inline void build(){
queue<int> q;
memset(fail,0,sizeof(fail));
for(int i=0;i<26;i++) if(tr[0][i]) q.push(tr[0][i]);
while(q.size()){
int top=q.front();q.pop();
for(int i=0;i<26;i++){
if(tr[top][i]){
fail[tr[top][i]]=tr[fail[top]][i];
q.push(tr[top][i]);
}
else tr[top][i]=tr[fail[top]][i];
}
}
}
inline void clear(){
memset(tr,0,sizeof(tr));
memset(end,0,sizeof(end));
memset(fail,0,sizeof(fail));
cnt=0;
}
inline int query(char *t){
int p=0,res=0;
for(int i=0;t[i];i++){
p=tr[p][t[i]-\'a\'];
for(int j=p;j;j=fail[j])
a[end[j]].sum++;
}
return res;
}
};
ACzdj ac;
int main(){
while(1){
memset(a,0,sizeof(a));
ac.clear();
int n=read();
if(!n) break;
for(int i=1;i<=n;i++){
scanf("%s",a[i].s);
ac.insert(a[i].s,i);
a[i].id=i;
}
ac.build();
scanf("%s",t);
ac.query(t);
sort(a+1,a+n+1);
printf("%d\\n",a[1].sum);
int now=1,minn=a[1].sum;
while(a[now].sum==minn){
printf("%s\\n",a[now].s);
now++;
}
}
}
对于例题 2,这个题我们在查询的时候直接这样像例题 1 做,会超时,正确的做法是我们把 fail 树建出来,然后在树上 dp 合并就可以了。
代码:
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<sstream>
#include<queue>
#include<map>
#include<vector>
#include<set>
#include<deque>
#include<cstdlib>
#include<ctime>
#define dd double
#define ld long double
#define ll long long
#define ull unsigned long long
#define N 1600000
#define M 10001000
using namespace std;
const int INF=0x3f3f3f3f;
inline int read(){
int x=0,f=1;
char ch=getchar();
while(ch<\'0\'||ch>\'9\'){if(ch==\'-\')f=-1;ch=getchar();}
while(ch>=\'0\'&&ch<=\'9\'){x=x*10+ch-\'0\';ch=getchar();}
return x*f;
}
struct edge{
int to,next;
inline void intt(int to_,int ne_){
to=to_;next=ne_;
}
};
edge li[N*10];
int head[N*10],tail;
inline void add(int from,int to){
li[++tail].intt(to,head[from]);
head[from]=tail;
}
struct rode{
int id,sum,belong,end;
};
rode a[N];
struct ACzdj{
int tr[N*10][26],cnt,size[N*10];
int end[N*10];int fail[N*10];
inline int insert(char *s,int id){
int p=0;
for(int i=0;s[i];i++){
int k=s[i]-\'a\';
if(!tr[p][k]) tr[p][k]=++cnt;
p=tr[p][k];
}
a[id].end=p;
if(!end[p]) end[p]=id;
else return end[p];
return id;
}
inline void build(){
queue<int> q;
memset(fail,0,sizeof(fail));
for(int i=0;i<26;i++) if(tr[0][i]) q.push(tr[0][i]);
while(q.size()){
int top=q.front();q.pop();
for(int i=0;i<26;i++){
if(tr[top][i]){
fail[tr[top][i]]=tr[fail[top]][i];
q.push(tr[top][i]);
}
else tr[top][i]=tr[fail[top]][i];
}
}
}
inline void clear(){
memset(tr,0,sizeof(tr));
memset(end,0,sizeof(end));
memset(fail,0,sizeof(fail));
cnt=0;
}
inline int query(char *t){
int p=0,res=0;
for(int i=0;t[i];i++){
p=tr[p][t[i]-\'a\'];
// for(int j=p;j;j=fail[j])
// a[end[j]].sum++;
size[p]++;
}
return res;
}
};
ACzdj ac;
inline void dp(int k){
for(int x=head[k];x;x=li[x].next){
int to=li[x].to;
dp(to);
ac.size[k]+=ac.size[to];
}
}
int n;
char s[M],t[M];
int main(){
n=read();
for(int i=1;i<=n;i++){
a[i].id=i;
scanf("%s",s);
a[i].belong=ac.insert(s,i);
}
ac.build();
scanf("%s",t);
ac.query(t);
for(int i=1;i<=ac.cnt;i++) add(ac.fail[i],i);
dp(0);
for(int i=1;i<=n;i++) printf("%d\\n",ac.size[a[i].end]);
// for(int i=1;i<=n;i++) printf("%d\\n",a[a[i].belong].sum);
return 0;
}
引用
以上是关于AC自动机的主要内容,如果未能解决你的问题,请参考以下文章