拦截导弹

Posted 2023-05-20 wscqwq

拦截导弹

贪心策略如下所示：图一表示具体做法，图二表示证明

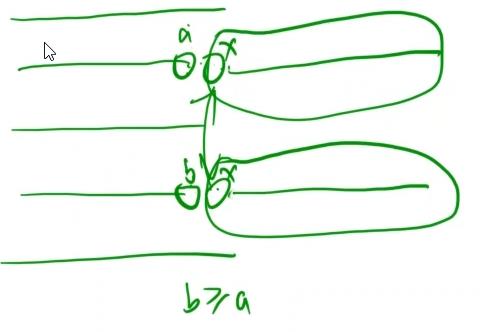
上图的证明是指，如果最优解和贪心存在第一个地方不一样，那么因为 \\(a\\) 是 \\(\\ge x\\) 的最小数，所以 \\(b\\ge a\\)，所以这两段是可以互换的，所以最优解是可以变成贪心的。

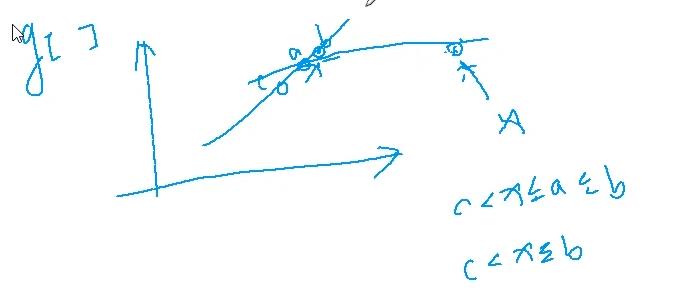
性质，\\(g\\) 数组单调不降，证明如上图。

我们可以惊奇的发现，这个步骤和 896. 最长上升子序列 II 的做法一致，所以就可以用那道题的做法；这道题其实是可以用二分优化的。

#include<bits/stdc++.h>
using namespace std;
int n,x,i,j,d[500001],ans,mid,a[500001],b[500001];
int main()
	while(cin>>a[++n]);
	n--;
	for(i=n;i>=1;i--)
		b[i]=a[n-i+1];
	for(i=1;i<=n;i++)
		if(b[i]>=d[ans])
			d[++ans]=b[i];
		else
			mid=upper_bound(d+1,d+1+ans,b[i])-d;
			d[mid]=b[i];	
		
	
	cout<<ans<<endl;
	ans=0;
	for(i=1;i<=n;i++)
		if(a[i]>d[ans])
			d[++ans]=a[i];
		else
			mid=lower_bound(d+1,d+1+ans,a[i])-d;
			d[mid]=a[i];	
		
	
	cout<<ans;
	return 0;

C语言 拦截导弹

题?? - 拦截导弹

来源 计算概论2006
描述
某国为了防御敌国的导弹袭击，开发出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷：虽然它的第一发炮弹能够到达任意的高度，但是以后每一发炮弹都不能高于前一发的高度。某天，雷达捕捉到敌国的导弹来袭，并观测到导弹依次飞来的高度，请计算这套系统最多能拦截多少导弹。拦截来袭导弹时，必须按来袭导弹袭击的时间顺序，不允许先拦截后面的导弹，再拦截前面的导弹。

关于输入
输入有两行：
第一行，输入雷达捕捉到的敌国导弹的数量k（k<=25），
第二行，输入k个正整数，表示k枚导弹的高度，按来袭导弹的袭击时间顺序给出，以空格分隔。

关于输出
输出只有一行，包含一个整数，表示最多能拦截多少枚导弹。

例子输入
8
300 207 155 300 299 170 158 65

例子输出
6

提示
无。

for (i=n-1;i>=1;i--)

for (j=n;j>=i+1;j--)

if (a[i]>a[j] && l[j]+1>l[i])

l[i]=l[j]+1;
//printf("%d %d\n",i,j);
max=0,ss=1;//for(i=1;i<=n;i++) printf("%d ",l[i]);printf("\n");
for (i=1;i<n;i++)


在这里有死循环，j永远小于i
---------------------------------------------------
/*
VC6.0编译运行成功
*/
#include
#include
/*
描述 Description
某国为了防御敌国的导弹袭击，研发出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷：虽然它的第一发炮弹能够到达任意的高度，但是以后每一发炮弹都不能高于前一发的高度。某天，雷达捕捉到敌国的导弹来袭。由于该系统还在试验阶段，所以只有一套系统，因此有可能不能拦截所有的导弹。
输入格式 Input Format
输入数据只有一行，该行包含若干个数据，之间用半角逗号隔开，表示导弹依次飞来的高度（导弹最多有 20 枚，其高度为不大于 30000 的正整数）。
输出格式 Output Format
输出数据只有一行，该行包含两个数据，之间用半角逗号隔开。第一个数据表示这套系统最多能拦截的导弹数；第二个数据表示若要拦截所有导弹至少要再添加多少套这样的系统。
样例输入 Sample Input
389,207,155,300,299,170,158,65
样例输出 Sample Output
6,1
其它测试输入样例
389,207,155,300,299,170,65,158
5,3,1,4,3,2,1,0
1,2,3,4,5,6,2
*/
/*
分析，问题是动态规划与Dilworth定理题目
http://www.gnocuil.cn/blog/article.asp?id=16
*/
int main()


char s[105];
int i, j, n, a[21], l[21], sign[21], max = 0, min = 0;
scanf("%s", s);
//min 代表最长递增序列长度 max 代表最短递减序列长度
for (i = 0, j = 0, a[0] = l[0] = sign[0] = 0; i < strlen(s); i++)


if (s[i] == ',')

a[++j] = 0;
sign[j] = 1;
l[j] = 1;


else

a[j] = a[j] * 10 + (s[i] - '0');


n = j;

for (i = n - 1; i >= 0; i--)

int maxflag = 0, minflag = 0;
j = i + 1;
while(j <= n)

if(a[i] > a[j])

if(l[i] < l[j])

l[i] = l[j];

maxflag = 1;

else if(a[i] < a[j])

if(sign[i] < sign[j])

sign[i] = sign[j];

minflag = 1;

j++;

if(maxflag)
l[i]++;

if(minflag)
sign[i]++;

if(max < l[i])

max = l[i];


if(min < sign[i])

min = sign[i];


printf("%d,%d\n", max, min - 1);
return (0);
参考技术A

1、求最长单调序列 简单动归（如果只求第二个的话用贪心也可以 ，不过动归可以两个一起做 而且代码更简单 ）。

2、例程：

#include<stdio.h>
#include<string.h>
#define N 21
int max(int mh[],int n) /* 求最多拦截导弹数 */

   int a[N][N],b[N],i,j,k,len1,s,t;
     /*   a:各系统可能拦截导弹的高度    b:各系统拦截导弹数   */ 
     /*    s:导弹拦截系统数 */
     /* len1:可拦截当前导弹的最优系统的编号(从0开始) */
     a[0][0]=mh[0]; s=1;   b[0]=1; 
     for (i=1;i<n;i++)
     
         len1=0;   t=0; 
         for (j=0;j<s;j++) /* j:系统编号 依次考查每套系统 */
   for (k=b[j]-1;k>=0;k-- ) /* 每套系统防御导弹高度数组编号 */
   
    if (mh[i]<=a[j][k])    
    
     if (t<k+1)
      t=k+1; len1=j;   break; 
     if (t==k+1)     
      if (a[len1][t-1]>a[j][k])
       len1=j;   break;      
    
   
         if (t!=b[len1])
    /* len1系统可拦截本高度前拦截数不等于已拦截数，则新建系统 */ 
                     
             for (k=0;k<t;k++)   
    a[s][k]=a[len1][k]; /* 新建系统的各个值 */
   a[s][t]=mh[i];
   b[s]=t+1;            
             s++;   
         
         else
                                     
             a[len1][(b[len1])]=mh[i];   /* 直接接在现有高度后 */ 
             b[len1]=b[len1]+1;
         
     
     t=0;
     for (i=0;i<s;i++)
         if (b[i]>t) t=b[i];
     return t;

int min(int mh[],int num)   /* 求需最少要配备导弹拦截系统数 */

     int s[21]=0,i,j,k,p;    
     k=1;
     s[0]=mh[0];
     for (i=1;i<num;i++)
     
         p=0;
         for (j=1;j<=k;j++)
             if ( (s[j-1]>mh[i]) &&( (p==0)||(s[j-1]<s[p-1]) ) )
                p=j;/*现有系统打击范围*/ 
         if (p==0)   
             
             k++;
             s[k-1]=mh[i];
         
            else s[p-1]=mh[i];
     
     return k;

main()

     int n,mh[N],i;   /* n为导弹数,数组mh为依次飞来的高度 */
     scanf("%d",&n);   
     for (i=0;i<n;i++)
         scanf("%d",&mh[i]);
     printf("%d   %d\\n",max(mh,n),min(mh,n));;
     system("pause");
     return 0;

参考技术B 完全了解你的情况，都是被计概习题逼的啊。
这里有一个同学编的程序，虽然很小，但非常巧妙，绝对可以pass，试试看吧。
但提醒一下：pass以后，请仔细读一读这个程序，知道它为什么可以通过好吗？
#include<stdio.h>
void main()
int b[26],k,h[26],t=0,i,j;
scanf("%d",&k);
for(i=1;i<=k;i++)
scanf("%d",&h[i]);
for(i=1;i<=k;i++)
for(j=1,t=0;j<i;j++)
if(h[j]>=h[i])
if(b[j]>t)
t=b[j];
if(t==0) b[i]=1;
else b[i]=t+1;
for(i=1,t=0;i<=k;i++)
if(b[i]>t)
t=b[i];
printf("%d",t);
本回答被提问者采纳 参考技术C #include<iostream>
using namespace std;
int main()
int i,j,n,x[100],d[100]; //x[]表示各个导弹高度，d[i]记录为第 i 枚导弹被拦截之后，
//这套系统最多还能拦截的导弹数（包含被拦截的第 i 枚）。
int dmax=0,xh=0; //记录拦截的最大个数以及第一个被拦截的序号
cin>>n; //输入拦截的导弹数
for(i=0;i<n;i++)
cin>>x[i]; //输入每个导弹的高度
d[i]=1;//初始值都设为1

for(i=n-2;i>=0;i--) //动态规划算法，递归实现,从后面向前循环
for(j=i+1;j<n;j++)
if((x[j]<x[i])&&(d[i]<d[j]+1)) //判断条件
d[i]=d[j]+1;

for(i=0;i<n;i++) //找出最大个数
if(d[i]>dmax)
dmax=d[i];
xh=i;//第一枚被拦截的导弹序号


cout<<d[xh]<<endl;
cout<<x[xh]<<",";
for(j=xh+1;j<n;j++) //依次输出满足条件的递减序号
if((x[j]<=x[xh])&&(d[xh]==d[j]+1)) //判断条件
cout<<x[j]<<",";
xh=j;

system("pause");
return 0;
参考技术D 例子输入
8
300 207 155 300 299 170 158 65

输入k个正整数，表示k枚导弹的高度，按来袭导弹的袭击时间顺序给出，以空格分隔。

例子输出
6
虽然它的第一发炮弹能够到达任意的高度，但是以后每一发炮弹都不能高于前一发的高度。
怎么能输出6?????明显是4
你这题本身就有问题..