用C试一下稀疏矩阵的快速转置

Posted 汀洲杜若

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了用C试一下稀疏矩阵的快速转置相关的知识，希望对你有一定的参考价值。

复习一下稀疏矩阵的快速转置操作。

稀疏矩阵使用三元组<行，列，数值>表示。简单起见下面代码使用固定长度的数组。

struct val3
   int x, y, e; ; 
struct mat3
    int row, col, count;
    val3 tab[MAXCOUNT]; ;
/*x是列，y是行，从零开始计数，row是矩阵有几行，col是有几列，count是矩阵中非零元的个数*/

先随机生成一个稀疏矩阵：

void init_mat31(mat3 *a)
    srand(time(NULL));
    a->row = rand() % (MAXROW - MINROW + 1) + MINROW;
    a->col = rand() % (MAXCOL - MINCOL + 1) + MINCOL;
    a->count = a->row * a->col * FACTOR; //FACTOR暂取0.05
    if(a->count < MINCOUNT) a->count = MINCOUNT;
    else if(a->count > MAXCOUNT) a->count = MAXCOUNT;
    for(int saved[MAXCOUNT+1],i,x,y, nsave=0,k=0; /*为矩阵生成数据*/
        k < a->count; nsave++, k++) 
again:  x = rand() % a->col, y = rand() % a->row; //生成行列位置
        saved[nsave] = (x << 16) | y; //行列不超过2^16
        for(i = 0; i < nsave; i++)
            if(saved[i] == saved[nsave])
                goto again; //如果位置重复那么重新生成
        a->tab[k].x = x, a->tab[k].y = y;
        a->tab[k].e = rand() % (a->row * a->col);

让三元组以升序排序，排序使用Key<行，列>。

int sort_mat3(mat3 *a)
    val3 *tab;
    int k, i, key, minpos, min;

    if(!(tab = (val3*)malloc(a->count*sizeof(val3))) return -1;
    memcpy(tab, a->tab, a->count * sizeof(val3));//一个副本
    k = 0;
    //使用选择排序，每次从tab选Key最小的三元组放入a->tab
again:
    // 找第一个没被选择过(*.x<0)的三元组
    for(minpos = 0;
minpos < a->count && tab[minpos].x < 0; minpos++);
    if(minpos == a->count) goto done;//找不到，结束排序
    min = (tab[minpos].y << 16) | tab[minpos].x;
    for(i = minpos + 1; i < a->count; i++) 
        if(tab[i].x == -1) // skip invalid items
            continue;
        key = (tab[i].y << 16) | tab[i].x; //使用(y<<16)|x做Key
        if(key < min)  min = key, minpos = i; 
    
    a->tab[k++] = tab[minpos];
    tab[minpos].x = -1; // 标记使其不再被选择
    goto again;
done:
    free(tab); return 0;

接着做快速转置。下面代码中的w表是关键。

int transpose(mat3 *a)
    val3* tab;
    int i, w[MAXCOL], pos;

    tab = (val3*) malloc(a->count * sizeof(val3));
    if(!tab) return -1;/*转置后的三元组先放在tab再复制到a->tab*/
    memset(w, 0, sizeof(int) * a->col);
    for(i = 0; i < a->count; i++)
        w[a->tab[i].x]++; //先统计各列非零元的个数存到 w
    for(pos=0, i=0; i < a->col; i++) 
        int nextpos = pos + w[i];
        w[i] = pos; //再计算转置后各列第一个非零元在a->tab的位置
        pos = nextpos;
    
    for(i = 0; i < a->count; i++)  /*根据w表执行转置*/
        int icol = a->tab[i].x;
        pos = w[icol];
        tab[pos].x = a->tab[i].y; tab[pos].y = a->tab[i].x;
        tab[pos].e = a->tab[i].e;
        w[icol]++;
    
    memcpy(a->tab, tab, a->count * sizeof(val3));
    i = a->row, a->row = a->col, a->col = i;
    free(tab); return 0;

好的，做个测试。

 还行。本来想整一个指针列表用地址排序，但是C的写法太不友好了，所以改用结构体struct val3的写法而不再用int tab[MAXCOUNT][3]的写法了（这样我就得写一个列表int (*ptr[MAXCOUNT])[3]，其元素是指针，这指针指向一个数组，这数组有三个整数，吐了）。

稀疏矩阵的列序递增法和一次定位快速转置法

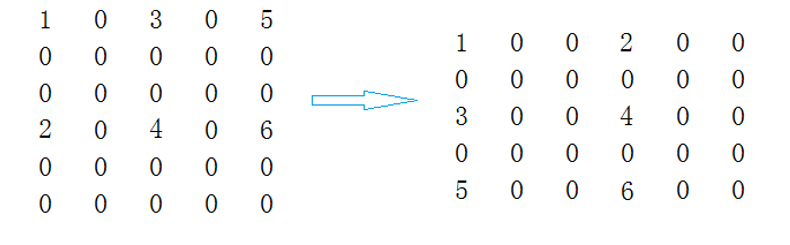
稀疏矩阵：矩阵中大多数元素为0的矩阵，从直观上讲，当非零元素个数低于总元素的30%时，这样的矩阵为稀疏矩阵。

如：

int array [6][5] =     {{1, 0, 3, 0, 5},                      

                        {0, 0, 0, 0, 0},                      

                        {0, 0, 0, 0, 0},                     

                        {1, 0, 3, 0, 5},                     

                        {0, 0, 0, 0, 0},                 

                        {0, 0, 0, 0, 0}};

稀疏矩阵的压缩存储：使用{row,col,value}三元组存储每一个有效数据，三元组按原矩阵中的位置，以行优先级先后顺序依次存放。

矩阵的转置：将原矩阵的行、列对换，也就是将[i][j]和[j][i]位置上的数据对换。

技术分享


稀疏矩阵的列序递增法：

    按照被转置矩阵三元组表A的序列（即转置后三元组表B的行序）递增的顺序进行转置，则转置后矩阵的三元组表B恰好是以“行序为主序的”.

一次定位快速转置法：

    在列转置中算法的时间浪费主要在双重循环中，要改善算法的性能，必须去掉双重循环，使得整个转置过程通过一次循环来完成。

为了使得被转置的三元组表A中元素一次定位到三元组表B中，需要计算一下以下数据：

1）RowCounts,三元组表A中每一列有效值的个数，即转置后矩阵三元组表B中每一行有效值的个数。

2）RowStart,三元组表B中每一行有效值的起始位置。

RowStart[i] = RowStart[i - 1] + RowCounts[i - 1];


代码实现：

#include <iostream>

using namespace std;

#include <vector>//动态数组


//三元组

template<class T>

struct Triple

{

size_t _row;

size_t _col;

T _value;


Triple(size_t row = 0, size_t col = 0, const T& value = T())

:_row(row)

, _col(col)

, _value(value)

{}

};


template<class T>

class SparseMatrix

{

public://invalid   非零值

SparseMatrix(T* a = NULL, size_t M = 0, size_t N = 0, const T& invalid = T())

:_rowSize(M)

, _colSize(N)

, _invalid(invalid)

{

for (size_t i = 0; i < M; ++i)

{

for (size_t j = 0; j < N; ++j)

{

if (a[i*N + j] != _invalid)//每行元素个数就是列的个数

{

Triple<T> t;

t._row = i;

t._col = j;

t._value = a[i*N + j];


_a.push_back(t);//在Vector类，插入一个元素

}

}

}

}


void Display()

{

size_t index = 0;


for (size_t i = 0; i < _rowSize; ++i)

{

for (size_t j = 0; j < _colSize; ++j)

{

if (index < _a.size()&& (_a[index]._row == i)&& (_a[index]._col == j))

{

cout << _a[index++]._value << " ";

}

else

{

cout << _invalid << " ";

}

}

cout << endl;

}

}


//矩阵列序递增转置算法，时间复杂度为O(有效数据的个数*原矩阵的列数)

SparseMatrix<T> Transport()

{

SparseMatrix<T> sm;

sm._colSize = _rowSize;

sm._rowSize = _colSize;

sm._invalid = _invalid;


for (size_t i = 0; i < _colSize; ++i)//列序递增

{

size_t index = 0;


while (index < _a.size())

{

if (_a[index]._col == i)

{

Triple<T> t;

t._row = _a[index]._col;

t._col = _a[index]._row;

t._value = _a[index]._value;


sm._a.push_back(t);

}

++index;

}

}

return sm;

}


//一次定位计数快速转置 时间复杂度为O(有效数据的个数+原矩阵的列数)

SparseMatrix<T> FastTransport()

{

SparseMatrix<T> sm;

sm._rowSize = _colSize;

sm._colSize = _rowSize;

sm._invalid = _invalid;


int* RowCounts = new int[_colSize];//计数

int* RowStart = new int[_colSize];//位置

memset(RowCounts, 0, sizeof(int)*_colSize);

memset(RowStart, 0, sizeof(int)*_colSize);


size_t index = 0;//index  非零元素

while (index < _a.size())

{

++RowCounts[_a[index]._col];

++index;

}


for (size_t i = 1; i < _colSize; ++i)

{

RowStart[i] = RowStart[i - 1] + RowCounts[i - 1];

}


index = 0;

sm._a.resize(_a.size());

while (index < sm._a.size())

{

Triple<T> t;

t._row = _a[index]._col;

t._col = _a[index]._row;

t._value = _a[index]._value;


sm._a[RowStart[_a[index]._col]] = t;


++RowStart[_a[index]._col];

++index;

}


delete[] RowCounts;

delete[] RowStart;


return sm;

}

protected:

vector<Triple<T>> _a;

size_t _rowSize;

size_t _colSize;

T _invalid;

};


void Test()

{

int array[5][4] =

{

{ 1, 0, 3, 0 },

{ 0, 0, 0, 0 },

{ 0, 0, 0, 0 },

{ 2, 0, 4, 5 },

{ 0, 0, 0, 0 },

};


SparseMatrix<int> sm1((int*)array, 5, 4, 0);

cout << "打印原矩阵："<<endl;

sm1.Display();

cout << endl;

cout << "打印转置后的矩阵：" << endl;

SparseMatrix<int> sm2 = sm1.Transport();

/*SparseMatrix<int> sm2 = sm1.FastTransport();*/

sm2.Display();

}


int main()

{

Test();

system("pause");

return 0;

}

运行结果：

打印原矩阵：

1 0 3 0

0 0 0 0

0 0 0 0

2 0 4 5

0 0 0 0


打印转置后的矩阵：

1 0 0 2 0

0 0 0 0 0

3 0 0 4 0

0 0 0 5 0

请按任意键继续. . .

两种算法比较：

    假设有效数据的个数为100，原矩阵的列数为100，矩阵列序递增转置算法，时间耗费为O(有效数据的个数*原矩阵的列数)，即100*100=10000次；一次定位计数快速转置算法，时间复杂度为O(有效数据的个数+原矩阵的列数)，即100+100=200次左右。显然一次定位计数快速转置算法的时间效率要高的多，在时间性能上优于列序递增转置法，但是在空间耗费上增加了两个辅助向量空间,即RowCounts和RowStart,由此可见，算法在时间上的节省是以更多的存储空间为代价的。


本文出自 “岩枭” 博客，请务必保留此出处http://yaoyaolx.blog.51cto.com/10732111/1775877

以上是关于用C试一下稀疏矩阵的快速转置的主要内容，如果未能解决你的问题，请参考以下文章

数据结构----稀疏矩阵的快速转置

稀疏矩阵的压缩存储及快速转置

稀疏矩阵的列序递增法和一次定位快速转置法

4.3.2 稀疏矩阵转置快速转置

关于稀疏矩阵三元组的转置

稀疏矩阵三元组快速转置（转poklau123写的很清楚）