m基于MSER最大稳定极值区域和SVM的交通标志检测识别算法的matlab仿真

Posted 2023-05-19 51matlab

1.算法仿真效果

matlab2022a仿真结果如下：

 

 

 

 

 

 

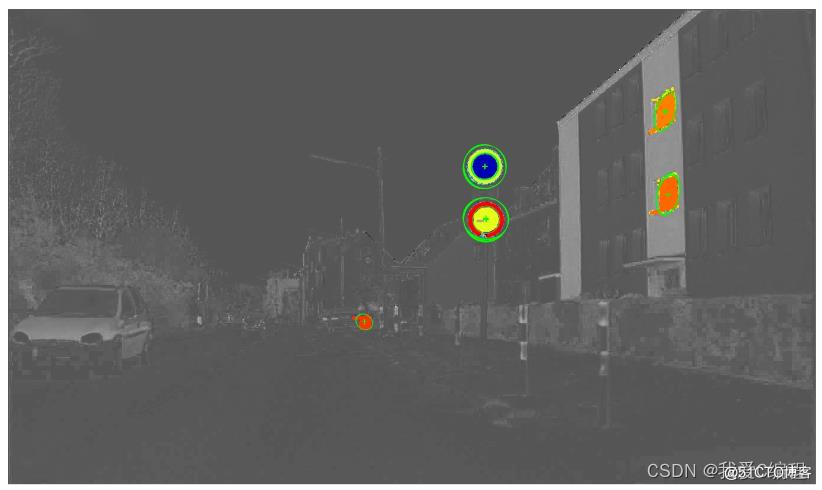
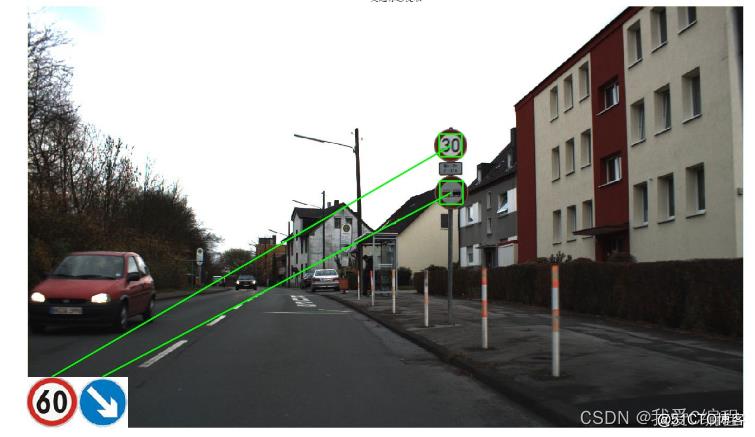
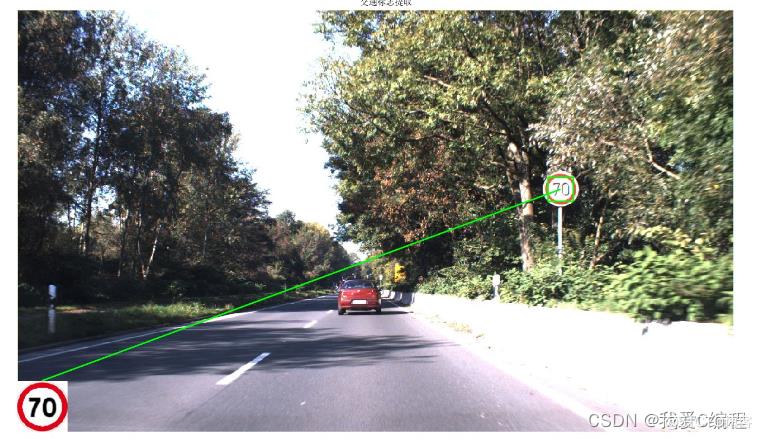
 2.算法涉及理论知识概要

        在计算机视觉领域，最大稳定极值区域 (MSER)(Maximally Stable Extremal Regions)是一种用于在图像中进行斑点检测的方法。这个方法由Matas等人提出，用于在两个不同视角的图片中寻找对应关系(correspondence problem)。这种方法从图像中提取全面的元素对应关系，有助于宽基线匹配(wide-baseline matching)，以及更好的立体匹配和物体识别算法。

       特征检测是计算机视觉和图像处理中的一个概念。它指的是使用计算机提取图像信息，决定每个图像的点是否属于一个图像特征。特征检测的结果是把图像上的点分为不同的子集，这些子集往往属于孤立的点、连续的曲线或者连续的区域。

       至今为止特征没有万能和精确的定义。特征的精确定义往往由问题或者应用类型决定。特征是一个数字图像中“有趣”的部分，它是许多计算机图像分析算法的起点。因此一个算法是否成功往往由它使用和定义的特征决定。因此特征检测最重要的一个特性是“可重复性”：同一场景的不同图像所提取的特征应该是相同的。

       特征检测是图象处理中的一个初级运算，也就是说它是对一个图像进行的第一个运算处理。它检查每个像素来确定该像素是否代表一个特征。假如它是一个更大的算法的一部分，那么这个算法一般只检查图像的特征区域。作为特征检测的一个前提运算，输入图像一般通过高斯模糊核在尺度空间中被平滑。此后通过局部导数运算来计算图像的一个或多个特征。

       有时，假如特征检测需要许多的计算时间，而可以使用的时间有限制，一个高层次算法可以用来控制特征检测阶层，这样仅图像的部分被用来寻找特征。

       由于许多计算机图像算法使用特征检测作为其初级计算步骤，因此有大量特征检测算法被发展，其提取的特征各种各样，它们的计算复杂性和可重复性也非常不同。

        MSER算法中，其最大稳定极值区域的定义为极值区域随着设置的灰度阈值的增大而逐渐“长大”。这样的一组极值区域由小到大是相互嵌套的关系，分别用来表示这一系列相互嵌套的极值区域序列。

 

        支持向量机（support vector machines, SVM）是二分类算法，所谓二分类即把具有多个特性（属性）的数据分为两类，目前主流机器学习算法中，神经网络等其他机器学习模型已经能很好完成二分类、多分类，学习和研究SVM，理解SVM背后丰富算法知识，对以后研究其他算法大有裨益；在实现SVM过程中，会综合利用之前介绍的一维搜索、KKT条件、惩罚函数等相关知识。本篇首先通过详解SVM原理，后介绍如何利用python从零实现SVM算法。

         实例中样本明显的分为两类，黑色实心点不妨为类别一，空心圆点可命名为类别二，在实际应用中会把类别数值化，比如类别一用1表示，类别二用-1表示，称数值化后的类别为标签。每个类别分别对应于标签1、还是-1表示没有硬性规定，可以根据自己喜好即可，需要注意的是，由于SVM算法标签也会参与数学运算，这里不能把类别标签设为0。

 

 

 

3.MATLAB核心程序

 

ind= 0;
for i = 1:length(XY)
    Xmin = min(XYi(:,1));
    Xmax = max(XYi(:,1));
    Ymin = min(XYi(:,2));
    Ymax = max(XYi(:,2));    
    W1(i)= Ymax - Ymin;
    L1(i)= Xmax - Xmin;
    if abs(L1(i) - W1(i)) <= 5
       ind      = ind+1; 
       XY2ind = XYi; 
    end
end
figure; 
imshow(I1); 
hold on;
for i = 1:length(XY2)
    plot(XY2i(:,1),XY2i(:,2),\'g.\');
    hold on
end
 
%提取交通标志的中心点，判断是否为同一个标志
for i = 1:length(XY2)
    Xmin(i)= min(XY2i(:,1));
    Xmax(i)= max(XY2i(:,1));
    Ymin(i)= min(XY2i(:,2));
    Ymax(i)= max(XY2i(:,2));
    Xc(i)  = (Xmin(i)+Xmax(i))/2;
    Yc(i)  = (Ymin(i)+Ymax(i))/2;
%     plot(Xc(i),Yc(i),\'r*\');hold on
end
 
%重合点合并
Xmin2=[];
Xmax2=[];
Ymin2=[];
Ymax2=[];
 
if length(Xc)>1
    indx = 0;
    for i = 1:length(Xc)
        tmps=[];
        for j = 1:length(Xc)
            if sqrt(double((Xc(i) - Xc(j))^2 + (Yc(i) - Yc(j))^2))<=20
               tmps=[tmps,j];
            end
        end
        tmps
        Xmin2(i) = mean(Xmin(tmps));
        Xmax2(i) = mean(Xmax(tmps));
        Ymin2(i) = mean(Ymin(tmps));
        Ymax2(i) = mean(Ymax(tmps)); 
    end
    %根据XYi的相似性进行合并
else
    Xmin2= Xmin;
    Xmax2= Xmax;
    Ymin2= Ymin;
    Ymax2= Ymax; 
end

 

　　

 

最大稳定极值区域（MSER）检测

Lowe和Bay提出的SIFT和SURF算法高效实现了具有尺度和旋转不变性的特征检测，但这些特征不具有仿射不变性。

区域检测针对各种不同形状的图像区域，通过对区域的旋转和尺寸归一化，可以实现仿射不变性。

MSER（Maximally Stable Extrernal Regions）是区域检测中影响最大的算法

1. 原理

MSER基于分水岭的概念：对图像进行二值化，二值化阈值取[0, 255]，这样二值化图像就经历一个从全黑到全白的过程（就像水位不断上升的俯瞰图）。在这个过程中，有些连通区域面积随阈值上升的变化很小，这种区域就叫MSER。

，其中Qi表示第i个连通区域的面积，Δ表示微小的阈值变化（注水），当vi小于给定阈值时认为该区域为MSER。

显然，这样检测得到的MSER内部灰度值是小于边界的，想象一副黑色背景白色区域的图片，显然这个区域是检测不到的。因此对原图进行一次MSER检测后需要将其反转，再做一次MSER检测，两次操作又称MSER+和MSER-

2. 算法步骤

从上节可以看到，MSER的基本思路很简单，但编码实现是很需要算法和编程技巧的

以下算法步骤基于改进的分水岭算法：注水的地方固定，只有当该处的沟壑水漫出来后才能注入到另一个沟壑

此外，为方便编程，面积变化的计算方式也从双边改为单边检测，即

具体步骤（摘自Opencv2.4.9源码分析——MSER）

1、初始化栈和堆，栈用于存储组块（组块就是区域，就相当于水面，水漫过的地方就会出现水面，水面的高度就是图像的灰度值，因此用灰度值来表示组块的值），堆用于存储组块的边界像素，相当于水域的岸边，岸边要高于水面的，因此边界像素的灰度值一定不小于它所包围的区域（即组块）的灰度值。首先向栈内放入一个虚假的组块，当该组块被弹出时意味着程序的结束；

2、把图像中的任意一个像素（一般选取图像的左上角像素）作为源像素，标注该像素为已访问过，并且把该像素的灰度值作为当前值。这一步相当于往源像素这一地点注水；

3、向栈内放入一个空组块，该组块的值是当前值；

4、按照顺序搜索当前值的4-领域内剩余的边缘，对于每一个邻域，检查它是否已经被访问过，如果没有，则标注它为已访问过并检索它的灰度值，如果灰度值不小于当前值，则把它放入用于存放边界像素的堆中。另一方面，如果领域灰度值小于当前值，则把当前值放入堆中，而把领域值作为当前值，并回到步骤3；

5、累计栈顶组块的像素个数，即计算区域面积，这是通过循环累计得到的，这一步相当于水面的饱和；

6、弹出堆中的边界像素。如果堆是空的，则程序结束；如果弹出的边界像素的灰度值等于当前值，则回到步骤4；

7、从堆中得到的像素值会大于当前值，因此我们需要处理栈中所有的组块，直到栈中的组块的灰度值大于当前边界像素灰度值为止。然后回到步骤4。


至于如何处理组块，则需要进入处理栈子模块中，传入该子模块的值为步骤7中从堆中提取得到的边界像素灰度值。子模块的具体步骤为：
1）、处理栈顶的组块，即根据公式2计算最大稳定区域，判断其是否为极值区域；
2）、如果边界像素灰度值小于距栈顶第二个组块的灰度值，那么设栈顶组块的灰度值为边界像素灰度值，并退出该子模块。之所以会出现这种情况，是因为在栈顶组块和第二个组块之间还有组块没有被检测处理，因此我们需要改变栈顶组块的灰度值为边界像素灰度值（相当于这两层的组块进行了合并），并回到主程序，再次搜索组块；
3）、弹出栈顶组块，并与目前栈顶组块合并；
4）、如果边界像素灰度值大于栈顶组块的灰度值，则回到步骤1。

注：MSER算法参数较多，默认值如图3-1所示（摘自《图像局部不变性特征与描述》）

图3-1. MSER参数标准取值

3. MSER区域拟合

为了进一步对MSER得到的不规则区域进行描述和处理，需要对其进行椭圆拟合（椭圆可以反映区域的位置、尺寸、方向）

1）椭圆的重心

对区域内的每个点，计算整个区域的几何0阶矩和几何一阶矩

得到整个区域的重心位置

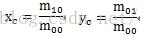
2） 椭圆的长半轴、短半轴、角度（长半轴与x轴顺时针）

计算中心二阶矩

其中

计算该二阶矩的两个特征值，有

于是可以分别得到其长半轴、短半轴、角度

4. 代码

目前MSER的代码实现有3：OpenCV（目前操作手册上还没有这个接口的介绍）、IDIAP的实现（C++）、VLFeat的实现（C）

其中OpenCV的代码解读可参考Opencv2.4.9源码分析——MSER，其和IDIAP的实现都严格遵循着上一节的算法步骤，

IDIAP的版本只有一个mser.cpp和mser.h，很干净便于移植（如果是C实现的就更好了），其在Github上声称比VLFeat快几倍。

VLFeat是一个C实现的图像特征检测算法库，包含了SIFT、HOG、K-Means、MSER等算法

贴上IDIAP和OpenCV实现的调用代码

#IDIAP

clock_t start = clock();

_MSER mser8(5, 0.0005, 0.5, 0.25, 0.2, true);
_MSER mser4(5, 0.0005, 0.5, 0.25, 0.2, false);

std::vector<_MSER::Region> regions[2];

mser8(imgBuffer, grayImg.cols, grayImg.rows, regions[0]);

// Invert the pixel values
for (int i = 0; i < grayImg.cols*grayImg.rows; ++i)
	imgBuffer[i] = ~imgBuffer[i];

mser4(imgBuffer, grayImg.cols, grayImg.rows, regions[1]);

clock_t stop = clock();

for (int i = 0; i < 2; ++i)
	for (int j = 0; j < regions[i].size(); ++j)
		//IDIAP自己实现的椭圆拟合函数
		drawEllipse(regions[i][j], img.cols, img.rows, 3, imgBufferRGB, colors[i]);

#OpenCV

cv::MSER ms(5, 0.0005, 1440);
std::vector<std::vector<cv::Point>> regions;

clock_t start = clock();
ms(grayImg, regions, cv::Mat());
clock_t stop = clock();

for (int i = 0; i < regions.size(); i++) 
	cv::ellipse(img, cv::fitEllipse(regions[i]), cv::Scalar(0, 0, 255));

从实际效果来看，运行效率 OpenCV > IDIAP，VLFeat没测试

图4-1左是IDIAP的实现效果（参数与代码中一致），右是OpenCV的实现效果（其余参数隐含在features2d.hpp内）

图4-1. MSER检测