常用排序算法的python实现
Posted yscl
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了常用排序算法的python实现相关的知识,希望对你有一定的参考价值。
排序算是编程最基本的算法问题之一了,熟练掌握排序算法也能加深自己对数据结构的理解,也能提高自己的编程能力,以下为个人参考许多大神博客后对常用排序算法的学习总结。
目录:
1. 概述
所谓排序(sorting)就是整理数据的序列,使其按照特定顺序排列的操作。排序在现实生活中(如整理书籍,表格数据等),在计算领域中(如二分查找,图论的最小生成树的Kruskal算法)均有重要意义,所以一种高效的排序算法就显得很有必要。
在排序过程中,如果待排序的序列全部保存在内存中,则成为内排序,如果用到了外部存储,则称为外排序。
排序算法的效率主要考虑空间复杂度,时间复杂度。即排序过程中比较次数和移动次数越少越好以及需要的辅助空间越少越好。
排序的稳定性也是排序的重要性质之一,排序后不改变原先的顺序则称该排序算法是稳定的,否则是不稳定的排序算法。比如待排序的序列不是简单的数,而是按照学生的成绩排序,如果两个学生成绩一样,排序后不应该改变原来学生的顺序,因为原来的序列中可能有有用的信息,排序后不应该打乱。
2. 冒泡排序
冒泡排序是对数据操作n-1趟,每趟找出最大或最小值,操作过程中,相邻数据两两比较,反序则交换,最大或最小的数随着每一轮的扫描便交换到了最后,整个过程就像冒泡一样,整个算法的时间复杂度是O(n^2), 空间复杂度是o(1)。稳定性方面冒泡并未交换相等的元素,是稳定的。
2.1 简单冒泡排序
def bubble_sort(lst): """最原始的冒泡排序""" length = len(lst) for i in range(length): for j in range(length - i - 1): if lst[j] > lst[j + 1]: lst[j], lst[j + 1] = lst[j + 1], lst[j]
2.2 改进的冒泡排序
对于原本就有序的序列,简单的冒泡排序仍然需要扫描n次序列,可以通过设置flag,当扫描的过程中没有发生交换动作,则说明已经有序了,最好情况时间复杂度为O(n)。
def bubble2_sort(lst): """改进的冒泡排序, 利用一个标志位, 当扫描一遍序列后没有发现逆序,则说明序列已经有序了""" length = len(lst) for i in range(length): swap = False for j in range(length - i - 1): if lst[j] > lst[j + 1]: lst[j], lst[j + 1] = lst[j + 1], lst[j] swap = True if not swap: break
2.3 交错冒泡排序
上面两种冒泡排序的效率都不高,第一因为反复交换做的赋值操作较多,第二则因为一些距离正确位置的较远的元素会拖累整个算法,所以可以通过交错冒泡,即一遍从左开始扫描序列,一遍从右开始扫描序列,使小的元素尽快的到达左边。
def stagger_bubble_sort(lst): """交错冒泡排序""" left_flag = True # 定义从左往右扫描的标志位 length = len(lst) left = 0 # 左边开始的位置 right = length # 右边开始的位置 for i in range(length): swap = False if left_flag: for j in range(left, right - 1): if lst[j] > lst[j + 1]: lst[j], lst[j + 1] = lst[j + 1], lst[j] swap = True right -= 1 else: for j in reversed(range(left + 1, right)): if lst[j] < lst[j - 1]: lst[j], lst[j - 1] = lst[j - 1], lst[j] swap = True left += 1 left_flag = not left_flag if not swap: break
3. 直接插入排序
插入排序则是将一个个元素不断地插入有序的序列中,最终得到一个有序序列。可以把只有一个元素的序列看做插入排序的初始有序序列。插入排序的时间复杂度为O(n^2),空间复杂度为O(1)。插入排序是稳定的算法。
def insert_sort(lst): n = len(lst) for i in range(1, n): j, temp = i, lst[i] while temp < lst[j - 1] and j > 0: lst[j] = lst[j - 1] j -= 1 lst[j] = temp
4. 简单选择排序
选择排序扫描n-1次未排序的的序列,每次选出最小(最大)的序列放在前面(后面),由于每次都需要比较n*(n-1)/2次,交换的次数只有一次,所以总的时间复杂度为o(n^2),空间复杂度为o(1)。在稳定性方面,是跳跃性的选择最值并交换,所以是不稳定的。简单选择排序效率总体是比冒泡排序高,但是不如插入排序。
def select_sort(lst): n = len(lst) for i in range(n - 1): k = i for j in range(i + 1, n): if lst[j] < lst[k]: k = j if k != i: lst[i], lst[k] = lst[k], lst[i]
5. 希尔排序
谈起希尔排序之前先说说一个逆序对的概念,所谓逆序对是指对于一个待排序列A的下标i,j,如果A[i] > A[j],则称(i,j)是一个逆序对。在前面的简单冒泡排序和简单插入排序中,每一次交换相邻元素可以理解为消去一个逆序对的过程,所以插入排序的时间复杂度是O(N+I),N是元素个数,至少需要扫描n次,I(Inversion)是指逆序对数量,当逆序对为0即原始序列基本有序时,时间复杂度就是O(n)。
有定理表明对于任意N个不同元素组成的序列平均具有N*(N-1)/4个逆序对,仅以交换相邻元素的算法的平均时间复杂度都为O(n^2)。所以想要提高效率,就可以一次消去多个逆序对来完成。希尔排序就是插入排序的改进版本,思想是每一次交换间隔为gap的两个元素使序列基本有序,最后进行一次间隔为1的插入排序。
下面是原始的希尔排序。
def shell_sort(lst): n = len(lst) gap = n // 2 while gap: for i in range(gap, n): j, temp = i, lst[i] while j >= gap and temp < lst[j - gap]: lst[j] = lst[j - gap] j -= gap lst[j] = temp gap //= 2
原始的希尔排序的选的增量很简单,就是每次减半,直到间隔为1。该算法的效率最坏情况是O(n^2),这也是不好的,举个最坏例子来看
原始序列 1 5 2 6 3 7 4 8
第一次增量为4 1 5 2 6 3 7 4 8
第二次增量为2 1 5 2 6 3 7 4 8
第三次增量为1 1 2 3 4 5 6 7 8
在上面这个序列中,增量元素不互质,可能对小增量根本不起作用,所以原始的希尔增量选取的不合适。
对于希尔排序有许多好的增量序列,例如Hibbard增量序列,增量Dk=2^k-1,相邻元素是互质的,还有Sedgewick增量序列,增量序列是{1, 5, 19, 41, 109...},猜想希尔排序的时间复杂度为O(7/6)。
对于希尔排序的稳定性,希尔排序的交换元素也是跳跃式的,所以也是一种不稳定的排序方式。下面是用Sedgewick增量序列的改进希尔排序。
def shell2_sort(lst): Sedgewick_seq = [1, 5, 19, 41, 109, 209, 505, 929, 2161, 3905, 8929, 16001, 36289, 64769, 146305, 260609, 587521] n = len(lst) for gap in reversed(Sedgewick_seq): for i in range(gap, n): j, temp = i, lst[i] while j >= gap and temp < lst[j - gap]: lst[j] = lst[j - gap] j -= gap lst[j] = temp
6. 堆排序
堆排序是选择排序的一种改进,原理是创建一个最大(最小)堆,每次用堆顶元素和最后一个元素交换,然后调整堆结构,创建堆的时间复杂度为O(n),每次调整堆的时间复杂度为O(log(n)),所以时间复杂度为O(nlog(n)),空间复杂度为O(1)。堆排序的交换元素是沿着完全二叉树的路径移动的,对应列表中就是跳跃的,所以也不是稳定的算法。下面是实现方法。
def heap_sort(lst): """堆排序""" n = len(lst) def siftdown(idx, n): """堆元素的下沉""" child = 2 * idx + 1 temp = lst[idx] while child < n: if child != n - 1 and lst[child] < lst[child + 1]: child += 1 if temp < lst[child]: lst[idx] = lst[child] else: break idx, child = child, 2 * child + 1 lst[idx] = temp def create_heap(): """创建最大堆""" for i in reversed(range(n // 2)): siftdown(i, n) create_heap() for j in range(1, n): lst[0], lst[-j] = lst[-j], lst[0] # 交换堆顶元素和最后一个元素 siftdown(0, n - j)
7. 归并排序
归并排序是把两个或多个有序序列合并为一个有序序列。
归并排序的思想是初始时把原始序列看成n个长度为1的有序序列,把这n个有序序列两两归并,最后有序序列个数减半,有序序列长度增加一倍,然后重复上面的操作,直到有序序列长度为n,数量为1为止。每次把两个有序序列归并,这又被称为二路归并。归并也是分治思想的一种典型应用。归并排序是一种稳定的排序算法,在时间复杂度上是O(nlog(n)),空间复杂度为O(n),因为借用了一个辅助空间。如下是归并排序的排序过程。
原始序列 5 1 2 6 8 9 3 4 0
第一步长度为1 1 5 2 6 8 9 3 4 0
第二步长度为2 1 2 5 6 3 4 8 9 0
第三步长度为4 1 2 3 4 5 6 8 9 0
第四步长度为8 0 1 2 3 4 5 6 8 9
归并排序通常有递归和非递归写法,下面是非递归的归并排序。
def merge_sort(lst): def m_merge(lfrom, lto, left, mid, right): """将lfrom[left, mid)和lfrom[mid, right)归并到lto中""" s, e = left, mid while left < e and mid < right: if lfrom[left] <= lfrom[mid]: lto[s] = lfrom[left] s, left = s + 1, left + 1 else: lto[s] = lfrom[mid] s, mid = s + 1, mid + 1 while left < e: lto[s] = lfrom[left] s, left = s + 1, left + 1 while mid < right: lto[s] = lfrom[mid] s, mid = s + 1, mid + 1 def merge_pass(lfrom, lto, length): """将lrom按length长度合并""" n = len(lfrom) i = 0 while i < n - 2 * length: m_merge(lfrom, lto, i, i + length, i + 2 * length) i += 2 * length if i + length < n: # 说明还剩下两段 m_merge(lfrom, lto, i, i + length, n) else: # 说明只剩下一段,不做处理直接加到最后 for j in range(i, n): lto[j] = lfrom[j] slen, n = 1, len(lst) temp = [None] * n while slen < n: merge_pass(lst, temp, slen) slen <<= 1 merge_pass(temp, lst, slen) slen <<= 1
8. 快速排序
快速排序是冒泡排序的升级版,也属于交换排序,与冒泡相比,快速排序就能一次性消除很多逆序数,从而达到减少总的交换次数以减少时间。
快速排序的思想是分治,通过某种标准将待排序的记录划分为大记录和小记录,以此不断递归,直到每个记录组只有一个的时候就自然有序了。算法的思路如下图所示
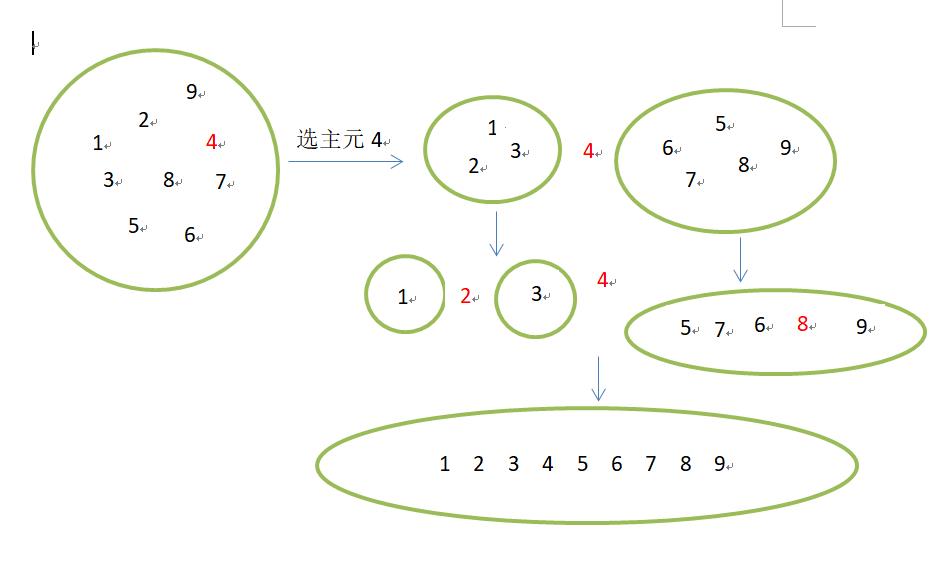
主元的选取: 从上可知,划分主元对于快排的效率很重要,例如每次都是取中间划分,最后需要划分log(n)次,总的时间复杂度就是nlog(n),如果划分不等,例如简单的取序列的第一个元素为主元,这样对原本就有序的序列最坏就需要划分n-1次,整个时间复杂度就是O(n^2),所以下面我是用取中位数的方式来获取主元的,即选取每段的左中右三个数的中间值作为主元,这样虽然不能完全消除最坏情况,但是降低了出现最坏情况的概率。
子集划分:初始把主元放到右边,i从左开始扫描碰到大于等于主元的停下来,j从右边开始扫描,遇到小于等于主元的元素时停下来,然后交换两元素,一直到i越过j停下,该位置即是主元正确的位置,最后与最后的主元交换。此处碰到相等的元素选择停下来交换是因为防止遇到所有元素相等的情况使得最后的划分子集又不均匀,最后时间复杂度趋于O(n^2)。

下面是快速排序的递归写法
def quick_sort(lst): """快速排序""" def get_pivot(left, mid, right): """获取主元pivot, 最后保证mid是处于中间的元素""" if lst[left] > lst[mid]: lst[left], lst[mid] = lst[mid], lst[left] if lst[left] > lst[right]: lst[left], lst[right] = lst[right], lst[left] if lst[mid] > lst[right]: lst[mid], lst[right] = lst[right], lst[mid] return lst[mid] def q_sort(left, right): if left >= right: return mid = (left + right) // 2 # 中间元素的下标 pivot = get_pivot(left, mid, right) # 获取主元 i, j = left + 1, right - 2 # 因为最后选择把主元交换到right-1的位置,两端经过筛选主元, 位置已经正确 if i <= j: # 从left+1和right-2的位置开始扫描 lst[mid], lst[right - 1] = lst[right - 1], lst[mid] # 主元交换到right-1的位置 while 1: while lst[i] < pivot: i += 1 while i <= j and lst[j] > pivot: j -= 1 if i < j: lst[i], lst[j] = lst[j], lst[i] i, j = i + 1, j - 1 else: break lst[i], lst[right - 1] = lst[right - 1], lst[i] # i是主元正确的位置,最后和right-1交换 q_sort(left, i - 1) # 递归地调用主元左边的记录 q_sort(i + 1, right) # 递归地调用主元右边的记录 q_sort(0, len(lst) - 1)
快速排序的非递归写法就是自己创建一个栈保存左右坐标,因为快排只关注这两个参数,而python的列表就可以充当栈的作用。
def quick3_sort(lst): """快速排序""" def get_pivot(left, mid, right): """获取主元pivot""" if lst[left] > lst[mid]: lst[left], lst[mid] = lst[mid], lst[left] if lst[left] > lst[right]: lst[left], lst[right] = lst[right], lst[left] if lst[mid] > lst[right]: lst[mid], lst[right] = lst[right], lst[mid] return lst[mid] def q_sort(left, right): partion = [(left, right)] # 把初始的左右坐标压入栈中 while partion: left, right = partion.pop() mid = (left + right) // 2 pivot = get_pivot(left, mid, right) # 选取中间作为主元 i, j = left + 1, right - 1 # 从left+1和right+1的位置开始左右扫描 if i < j: lst[mid], lst[i] = lst[i], lst[mid] # 此处与上面方法又稍微有所不同,选择把主元放入左边第一个位置 while i < j: while i < j and lst[j] > pivot: # 扫描寻找小于等于主元的数并停下来 j -= 1 if i < j: lst[i] = lst[j] # 用刚寻找到的小的数覆盖左边i的位置,i下标加1 i += 1 while i < j and lst[i] < pivot: # 寻找大于等于主元的数并停下来 i += 1 if i < j: # 用刚找到的大数覆盖右边j的位置, j的下标并减1 lst[j] = lst[i] j -= 1 lst[i] = pivot # 最后一定是i==j时跳出循环,此时的i就是主元正确的位置 if left < i - 1: partion.append((left, i - 1)) # 左右坐标压栈 if i + 1 < right: partion.append((i + 1, right)) # 压栈 q_sort(0, len(lst) - 1)
快速排序的实现方法还有一种简单的方法,思路如下所示
Pivot | < Pivot | >= Pivot | 未处理的数据
i j
将一组待处理的数据划分为4段,第一个位置是主元,第二段是小于主元的元素,第三段是大于等于主元的元素,第4段是未处理的数据,需要用到两个辅助指针i和j,i总是指向小于主元的最后一个元素,j总是指向未处理数据的第一个元素,j从主元后一个位置开始扫描,每次比较该元素和主元的的大小,当大于等于主元时,则简单的将j+1, 否则,先将i+1,然后交换i和j的元素,让小的元素移动到左边,再将j+1,重新恢复到上面4段的情况。最后当未处理数据全部扫描完后,交换主元和i的位置,整个数据记录也就划分成了小记录和大记录两段。整个代码如下所示.
def quick2_sort(lst): def get_pivot(left, mid, right): """获取主元pivot""" if lst[left] > lst[mid]: lst[left], lst[mid] = lst[mid], lst[left] if lst[left] > lst[right]: lst[left], lst[right] = lst[right], lst[left] if lst[mid] > lst[right]: lst[mid], lst[right] = lst[right], lst[mid] return lst[mid] def qsort(left, right): if left >= right: return mid = (left + right) // 2 pivot = get_pivot(left, mid, right) i = left + 1 if left + 2 < right: lst[i], lst[mid] = lst[mid], lst[i] # 把主元换到首位 for j in range(left + 1, right): if lst[j] < pivot: i += 1 lst[i], lst[j] = lst[j], lst[i] lst[i], lst[left + 1] = lst[left + 1], lst[i] qsort(left, i - 1) qsort(i + 1, right) qsort(0, len(lst) - 1)
9. 算法的比较与测试
为了测试的公平性,选择随机生成数据,并保存到文件中,使每种算法对同一数据进行排序比较。
随机生成测试数据
def generate_data(file=\'numbers.json\', size=5000): """产生随机数据, 存到文件中""" lst = [random.randint(0, size) for i in range(size)] json.dump(lst, open(file, \'w\', encoding=\'utf-8\'))
算法的计时用一个装饰器完成。
def exectime(func): """一个计时的装饰器函数""" def inner(*args, **kwargs): s = time.perf_counter() res = func(*args, **kwargs) cost_time = time.perf_counter() - s print("%s time: %.3f" % (func.__name__, cost_time)) return res inner.__name__ = func.__name__ # 此处是防止装饰器函数的inner覆盖原函数的名字 return inner
因为上面各种排序算法的名字很有规律,所以我利用反射写进一个函数统一测试。
def test(): m = sys.modules[\'__main__\'] # 获取当前模块的引用 sort_func = [] # 保存排序函数的引用 for k, v in m.__dict__.items(): if k.endswith(\'sort\'): # 排序算法的名字都已sort结尾,加入到列表中 sort_func.append(v) sort_func.sort(key=lambda x: x.__name__) # 根据排序算法的名字排序 for func in sort_func: data = json.load(open(\'numbers.json\')) # 每次重新读取文件里的数据 func(data) print(data) # 数据过多时可以不打印,此处作为调试的作用
下面是完整代码

1 """总结各种排序算法""" 2 import random 3 import sys 4 import time 5 import json 6 7 8 def generate_data(file=\'numbers.json\', size=5000): 9 """产生随机数据, 存到文件中""" 10 lst = [random.randint(0, size) for i in range(size)] 11 json.dump(lst, open(file, \'w\', encoding=\'utf-8\')) 12 13 14 def exectime(func): 15 """一个计时的装饰器函数""" 16 def inner(*args, **kwargs): 17 s = time.perf_counter() 18 res = func(*args, **kwargs) 19 cost_time = time.perf_counter() - s 20 print("%s time: %.3f" % (func.__name__, cost_time)) 21 return res 22 inner.__name__ = func.__name__ # 此处是防止装饰器函数的inner覆盖原函数的名字 23 return inner 24 25 26 @exectime 27 def bubble_sort(lst): 28 """最原始的冒泡排序""" 29 length = len(lst) 30 for i in range(length): 31 for j in range(length - i - 1): 32 if lst[j] > lst[j + 1]: 33 lst[j], lst[j + 1] = lst[j + 1], lst[j] 34 35 36 @exectime 37 def bubble2_sort(lst): 38 """改进的冒泡排序, 利用一个标志位, 当扫描一遍序列后没有发现逆序,则说明序列已经有序了""" 39 length = len(lst) 40 for i in range(length): 41 swap = False 42 for j in range(length - i - 1): 43 if lst[j] > lst[j + 1]: 44 lst[j], lst[j + 1] = lst[j + 1], lst[j] 45 swap = True 46 if not swap: 47 break 48 49 50 @exectime 51 def stagger_bubble_sort(lst): 52 """交错冒泡排序""" 53 left_flag = True # 定义从左往右扫描的标志位 54 length = len(lst) 55 left = 0 56 right = length 57 for i in range(length): 58 swap = False 59 if left_flag: 60 for j in range(left, right - 1): 61 if lst[j] > lst[j + 1]: 62 lst[j], lst[j + 1] = lst[j + 1], lst[j] 63 swap = True 64 right -= 1 65 else: 66 for j in reversed(range(left + 1, right)): 67 if lst[j] < lst[j - 1]: 68 lst[j], lst[j - 1] = lst[j - 1], lst[j] 69 swap = True 70 left += 1 71 left_flag = not left_flag 72 if not swap: 73 break 74 75 76 @exectime 77 def insert_sort(lst): 78 n = len(lst) 79 for i in range(1, n): 80 j, temp = i, lst[i] 81 while temp < lst[j - 1] and j > 0: 82 lst[j] = lst[j - 1] 83 j -= 1 84 lst[j] = temp 85 86 87 @exectime 88 def select_sort(lst): 89 n = len(lst) 90 for i in range(n - 1): 91 k = i 92 for j in range(i + 1, n): 93 if lst[j] < lst[k]: 94 k = j 95 if k != i: 96 lst[i], lst[k] = lst[k], lst[i] 97 98 99 @exectime 100 def shell_sort(lst): 101 n = len(lst) 102 gap = n // 2 103 while gap: 104 for i in range(gap, n): 105 j, temp = i, lst[i] 106 while j >= gap and temp < lst[j - gap]: 107 lst[j] = lst[j - gap] 108 j -= gap 109 lst[j] = temp 110 gap //= 2 111 112 113 @exectime 114 def shell2_sort(lst): 115 Sedgewick_seq = [1, 5, 19, 41, 109, 209, 505, 929, 2161, 3905, 8929, 16001, 36289, 64769, 146305, 260609, 587521] 116 n = len(lst) 117 for gap in reversed(Sedgewick_seq): 118 for i in range(gap, n): 119 j, temp = i, lst[i] 120 while j >= gap and temp < lst[j - gap]: 121 lst[j] = lst[j - gap] 122 j -= gap 123 lst[j] = temp 124 125 126 @exectime 127 def heap_sort(lst): 128 """堆排序""" 129 n = len(lst) 130 131 def siftdown(idx, n): 132 """堆元素的下沉""" 133 child = 2 * idx + 1 134 temp = lst[idx] 135 while child < n: 136 if child != n - 1 and lst[child] < lst[child + 1]: 137 child += 1 138 if temp < lst[child]: 139 ls以上是关于常用排序算法的python实现的主要内容,如果未能解决你的问题,请参考以下文章
