从零开始学习PYTHON3讲义画一颗心送给你
Posted 月色的流浪空间
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了从零开始学习PYTHON3讲义画一颗心送给你相关的知识,希望对你有一定的参考价值。

(内容需要,本讲使用了大量在线公式,如果因为转帖网站不支持公式无法显示的情况,欢迎访问原始博客。)
《从零开始PYTHON3》第十二讲
上一节课我们主要讲解了数值计算和符号计算。数值计算的结果,很常用的目的之一就是用于绘制图像,从图像中寻找公式的更多内在规律。
Python科学绘图
科学绘图是计算机图形学的一个重要分支。同其它绘图方式相比,更简单易用,能让使用者把工作的主要精力集注在公式和算法上而不是绘图本身。此外科学绘图的工具包普遍精度更高,数据、图的对应关系准确,从而保证基于图的研究工作顺利进行。最后,科技绘图一般都使用同数学相同的坐标系,避免了不必要的数据转换。
常用的一个高质量科学绘图包是第三方出品的MatplotLib,安装方式跟其它扩展库相同(这里只示例基于Windows环境的安装):
#首先使用管理员模式执行cmd命令行,随后在命令行执行:
pip install matplotlib #某些系统需要使用pip3所有的绘图,无论是基于显示器还是打印机(绘图仪),都可以看做一个宽*高的二维矩阵。这就产生了一个坐标系统,那么矩阵中的任意一个点,就会有坐标(x,y),x代表横方向坐标,y轴代表纵向坐标。
三维的游戏、VR等应用,在计算的整个过程中使用的是x、y、z三维坐标体系,但最后绘制到屏幕上的时候,还是会根据透视缩放的映射关系,将图像投影到二维矩阵中。
那么一副图像,就是有很多个点组成的,每个点都有其x,y的坐标。如果组成一个列表,通常是[[x1,y1],[x2,y2],[x3,y3]]这样的形式,比如刚才这个例子就代表了3个点的列表。如果是一条线,则可以用[[x1,y1],[x2,y2]]两个点来描述,这两个点就是一条线的两个端点坐标。
在我们今天讲的数学绘图中,通常使用的是另外一种坐标表示方法。科学绘图会使用x坐标点的列表和y坐标点的列表,两个列表来描述一组点。比如:[x1,x2,x3],[y1,y2,y3]。
即便只有一个点,也要把x坐标和y坐标分开到两个列表中去,此时列表就成为只有一个元素的列表,[x],[y]。
使用这种数据结构的原因是这样的,比如我们试图绘制函数:
$$
y = f(x)
$$
的图像。通常的情况我们首先是有一列的x值,那么通过函数计算之后,组成的就是一个结果y的列表。
因此事实上,为函数绘制图像,我们不大可能跟传统图像一样,上来就有一个完整的坐标点列表,而只能是x、y两个列表。列表中相同下标的值,是对应的x、y坐标,而y坐标的值,来自于上面所示函数对于x列表的计算结果。以一个3坐标的列表为例,大致是[x1,x2,x3],[y1,y2,y3]这样的形式。
言语总是枯燥无味的,让我们来看一段代码,用于绘制一副正弦函数图:
#绘制正弦曲线
#引入数值计算库,改为短名称
import numpy as np
#引入绘图库,改为短名称
import matplotlib.pyplot as plt
#生成一个由-4到4、均分为200个元素的列表
x = np.linspace(-4, 4, 200)
#计算当x取值范围-4至4时所有的sin函数解
f = np.sin(x)
#绘制
plt.plot(x, f, ‘red‘)
#将绘制好的图显示出来
plt.show()有几条命令再更详细的解释一下:
- np.linspace函数我们在讲数值计算的时候学过,是生成一个200个元素的列表,这个列表是numpy库的列表类型,跟python内置的列表是基本兼容的,但并不是同一种类型。这200个元素均分了从-4到+4的值范围,包含了-4/+4本身。
- np.sin(x),看起来跟内置的math.sin(x)很像,事实上当x是一个数字变量的时候,两者完全相同。但在这里,x是一个列表,包含200个元素。那两者就完全不同了。内置的math.sin一次调用只能处理一个数字。np.sin是一次处理整个数组。因此调用完成后,结果f中是包含了200个值,每个相同下标的值,是对应x列表中对应下标值的正弦函数结果值。所以f在这里实际就是y坐标的值。
- 终于看到了plt.plot函数,里面有三个参数,x是x坐标列表,本例中包含了200个元素,f实际是y轴坐标列表,也包含了200个元素,最后的‘red‘表示使用红色绘制。此函数在绘制这个数组的时候,每两个点之间,默认会使用直线连接上,从而让整体上形成一条平滑的曲线。
- 最后plt.show()是把绘制好的图形显示出来,此语句之后的绘图将被忽略掉,所以请确保这一条语句是所有plt调用的最后一句。
绘制的结果请看下图。
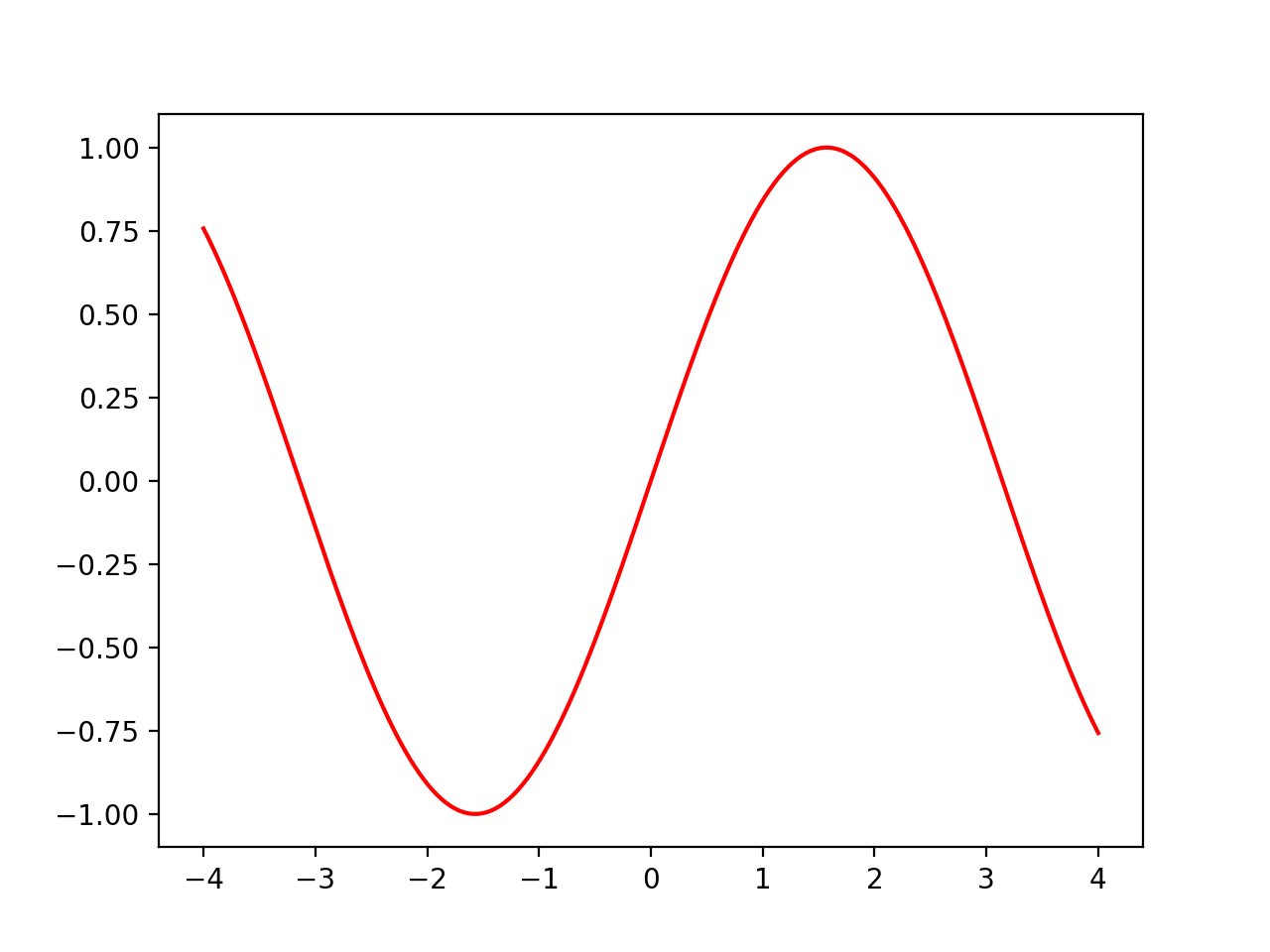
干净漂亮的正弦曲线出现了!
Python的学习一定要多动手练习,所以请自己也来来试试绘制过程。比如改变参数范围从-10到+10,比如把200个列表元素改成只有10个,看看是什么效果?
我们继续为这个画面做一些辅助性的补充。请把下面的代码加到plt.show()语句之前:
#为某条曲线增加注释文字
plt.text(1.3, 0.9, ‘sin(x)‘,color=‘b‘)
#为整个图增加标题
plt.title(‘y=f(x)‘, fontsize=16)只加了两行代码。第一行代码是在画面中增加注释性的文字,其实只有一条曲线意义并不大。但多条曲线,如果没有注释的文字,看起来就很困难了。第一行代码里面,头两个参数是坐标,表示注释文字出现的起始位置,这个坐标的单位就是正弦曲线的数学值,这一点,在其它绘图系统中都是要做很复杂的变换才能搞的定,在这里直接用就好了;第三个参数是显示的文字;第四个参数“b”代表blue,意思是用蓝色显示注释文字,这是想告诉你,其实前面的“red”,一样可以简写成“r”。
第二行代码视为整个画面增加一个标题,标题会显示在图片的上方中间的位置,第二个参数给了个字体尺寸,其实第二个参数可以没有,那样的话会自动给出一个适合标题的尺寸,一般都适于大多数情况使用。
有一点需要注意,画面中的注释文字,和标题,都不能直接支持中文。通常国外的软件,或多或少支持其它语言文字都有小问题。解决也并不难,就是需要指定使用中文的字体,这个超出了本课程的范围,有兴趣了解的可以参考教学资源包中的demo.py程序,注意字体的设置,是跟操作系统相关的,不具备可移植性。
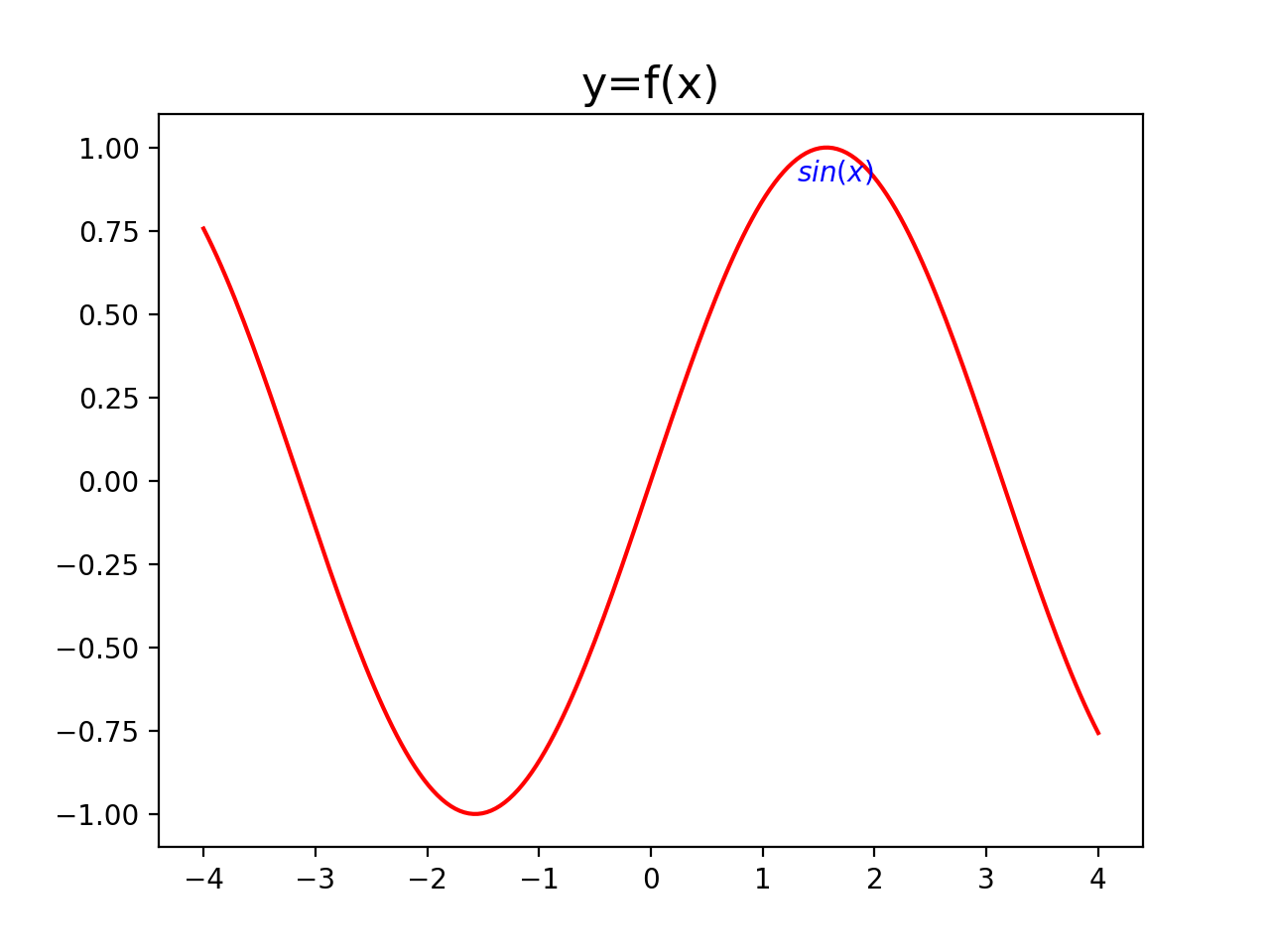
上图是增加了注释文字和标题之后的效果。你可能注意到了,图片窗口中有菜单是可以直接保存图片的。这样的图片直接引用到论文中效果一流。
科学绘图库我们使用了已经内置的正弦函数作为示例开始,这样为了降低使用的难度,专注解释绘图操作的机理。
在实际应用中,要绘制的通常都是很复杂的数学公式,这时候前面讲过的数学内容就用得上了。建议你自己定义一个函数,把复杂的公式,使用Python描述出来。注意因为要绘图,所以通常都是需要使用数值计算库而不是符号计算库。
下面我们举一个例子,简单起见,我们只使用最简单的直线公式(仅为示例,单纯画直线有很多更好的办法):
$$
y=ax+b
$$
#绘制直线
#引入数值计算库
import numpy as np
#引入绘图库
import matplotlib.pyplot as plt
#定义一个直线函数
def line(x,a,b):
return a*x+b
#我们用于示例,定义的函数没有计算数组的功能
x1=-4
y1=line(x1,0.2,0)
x2=4
y2=line(x2,0.2,0)
#绘制直线,只需要两个端点
plt.plot([x1,x2],[y1,y2],‘r‘)
#增加注释文字
plt.text(-3.9, -0.8, ‘0.2*x‘,color=‘r‘)
#为整个图增加标题
plt.title(‘y=ax+b‘, fontsize=16)
#将绘制好的图显示出来
plt.show()整体的程序结构跟上面画正弦函数的几乎相同。区别有两点,1是使用自定义的函数替代np.sin函数;2是计算的时候,因为我们自己定义的函数不支持数组运算,所以自己要逐次计算每个点。好在是直线,只要计算两个点就成了。
此外有一点要说明的,我们前面其实提到过,plt.plot函数,会自动连接每个点,使得整体成为连贯的线条,所以这个绘图示例的结果,我们给出两个点,最终得到了一条线。下面是运行结果:
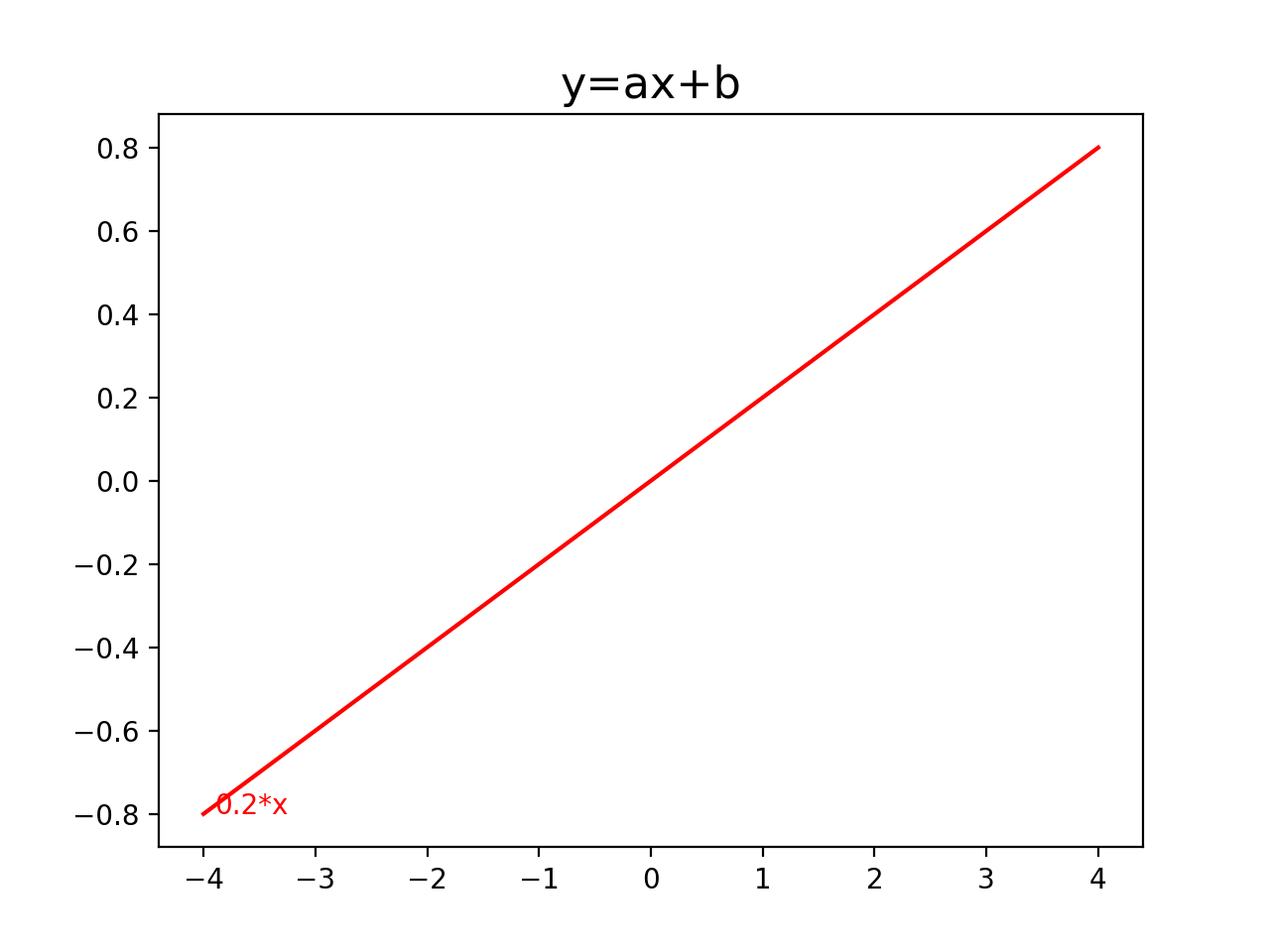
一个小思考题,排除这个直线函数。如果我们自己定义的函数式曲线,那肯定还是需要自己定义的Python函数,除了实现函数的计算,还要能实现数组的计算比较合理,这应当如何做呢?最好能用自己定义的函数来说明一下,或者用伪代码来描述一下也可以接受。
科技绘图部分的最后,推荐去官方网站看一看经典的“绘图画廊”,都是使用MatplotLab绘制的,都附有源代码,而且程序还都不算长,相信会让你很有收获。多说一句,Python的内置函数和第三方函数总量浩如烟海,你看别人程序的时候肯定会碰到很多不理解的函数或者关键字,基本的语法我们都已经学过了,这些不明白的内容求助搜索引擎,一定能让你快速的找到答案。
海龟绘图
今天一开始讲的科学绘图工具包非常强大。Python也内置了一套简单易用的绘图包,名字是海龟绘图,库名为:turtle,内置库无需安装,直接在程序一开始引用就可以了。
海龟绘图是在上世纪90年代非常流行的一套儿童绘图工具包,曾经风靡一时,但可惜在当今各种高级工具层出不穷的情况下,已经比较没落了。
但我的感觉是对于初学者,还是有很多参考意义,所以下面的内容,着重了解和动手尝试,对于具体的内容,有兴趣当然可以学习,兴趣不足的,练练手就好了,不要求你重点记忆。
海龟绘图的基本理念是这样:想象沙滩上有只小海龟。它只会向前走、转向等简单的动作,它在沙滩上爬行所留下的轨迹就是绘制出的图形(其实绘图命令中还有抬起画笔、放下画笔等操作,有兴趣的使用help(turtle)可以查看完整帮助)。
这种模式很适合使用循环语句绘制螺旋线等规律几何结构,如果设计得当,可以得到很多炫目的几何图形。我们来看几个例子:
#海龟绘图演示
#引入海龟绘图库
import turtle
#建立一支笔(一只海龟)
t = turtle.Pen()
for x in range(100):
#向前走x步
t.forward(x)
#左转90度
t.left(90)
turtle.done()上面就是在第一讲中我们介绍过的图形,绘制结果为:

换一个算法再看看:
#海龟绘图演示
#引入海龟绘图库
import turtle
#建立一支笔(一只海龟)
t = turtle.Pen()
t.pencolor(‘red‘)
for x in range(100):
#向前走x步
t.forward(x)
#左转90度
t.left(95)
turtle.done()注意这个程序中有了设置画笔颜色的语句。下面是绘制结果:
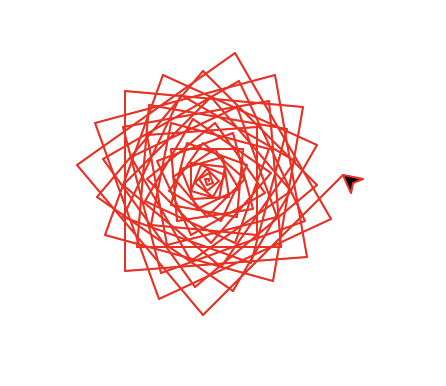
除了设置画笔的颜色,还可以设置画笔所封闭的区域中的填充颜色,请看这个例子和执行的结果:
#引入绘图库
from turtle import *
#设置笔的颜色和填充颜色
color(‘red‘, ‘yellow‘)
#开始填充
begin_fill()
while True:
forward(200)
left(170)
#pos是当前海龟坐标
#abs(pos())表示判断如果
# 海龟回到原点附近则停止
if abs(pos()) < 1:
break
#结束填充
end_fill()
done()
这些例子中,基本都使用了循环结构,希望你还记得循环的语法、边界条件、循环体这些概念,并以此读懂这些例子的原理。
在上面最后的例子中,有一些需要补充的。pos()返回当前小海龟的位置(x,y),是以数学复数的方式返回的。复数不在我们学习计划内,所以这部分内容了解即可,大致原理:abs(pos())实际是计算sqrt(x * 2+y * 2),也既当前坐标到原点的直线距离。所以上面例子中,使用这个方法来判断小海龟画笔,回到了原点附近,表示整个曲线绘制完整、并且头尾连贯、闭合了。因为只有闭合的区域,才可能填充颜色。
本节课总体上都是很轻松愉悦的。相信你经过前面艰苦的学习,已经尝到了收获的滋味,我们也到了收获的季节。娱乐起见,我们再提供一个网上转帖的海龟绘图程序,用于绘制小猪佩奇(程序比较长,请直接参考paige.py,此处感谢原作者):

小猪佩奇的程序中,使用了很多海龟绘图的缩写功能,比如forward向前走命令可以缩写为fd,向左转命令left可以缩写为lt。这些在help(turtle)文档中都能查到。缩写只是为了编写程序时候的方便,功能是完全一样的。
除了前面讲过的规则几何图案,想绘制这种定制的图形,通常都需要使用“坐标纸”,现在除了上淘宝,估计平常的商店都买不到了。然后把想绘制的图形描绘在坐标纸上,从而获得每个点的准确坐标。接下来就可以利用这些坐标,利用抬笔、移动坐标、落笔的功能,绘制定制的图形了。
不过可惜啊,现在有了Photoshop之类的软件,像坐标纸描格子的过程,都足以在屏幕上绘制完成了,完全不需要编程的知识。这也是海龟绘图逐渐没落的原因。
练习时间
1.请绘制下面函数的图像:
$$
y=sqrt{1-(|x|-1)^2},arccos(1-|x|)-pi
$$
这里解释一下:
- y是两个公式,用逗号隔开,表示取值是两个,程序中应当分别计算,得到两组值
- x取值空间建议:-2至2
- 根号函数:numpy.sqrt(),绝对值:numpy.fabs()
- 平方:numpy.square(),同**2的区别,后者只计算一个值,前者计算整个列表
- 其它函数:numpy.arccos,常量π:numpy.pi
2.海龟绘图的练习,其实在第一讲的时候我们练习过一些了,现在学习了这么多,再来试试吧
A.修改前面例程的简单参数,构建有趣的规则几何图形
B.开动脑筋,重新编程,绘制一副更有创意的图形
本讲小结
- 图形、图像是计算机科学中重要的组成部分
- 科技绘图用途广泛,也是理工学习中必须用到的内容
- 海龟绘图简单有趣,能显示绘图过程,适合简单创意性的场合
练习答案
1.课程中的思考题,在自定义函数中,应当使用循环,遍历参数的所有元素,逐个代入数学公式中计算,得到的结果逐个加入已经预先定义好的空列表中,最终返回这个完整的列表。程序代码略。
2.请参考ex1.py程序
3.海龟绘图练习略
以上是关于从零开始学习PYTHON3讲义画一颗心送给你的主要内容,如果未能解决你的问题,请参考以下文章