R语言逐步多元回归模型分析长鼻鱼密度影响因素|附代码数据
Posted 大数据部落
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了R语言逐步多元回归模型分析长鼻鱼密度影响因素|附代码数据相关的知识,希望对你有一定的参考价值。
原文链接:http://tecdat.cn/?p=9564
最近我们被客户要求撰写关于多元回归的研究报告,包括一些图形和统计输出。
我从马里兰州生物流调查中提取了一些数据,以进行多元回归分析。数据因变量是每75米长的水流中长鼻鱼(Rhinichthys cataractae)的数量。自变量是河流流失的面积(英亩);氧浓度(毫克/升);水流段的最大深度(以厘米为单位);硝酸盐浓度(毫克/升);硫酸盐浓度(毫克/升);以及采样日期的水温(以摄氏度为单位)
目录
如何做多元回归
逐步回归选择模型
逐步程序
定义最终模型
方差分析
预测值图
检查模型的假设
模型拟合标准
将模型与似然比检验进行比较
如何做多元回归
多重相关
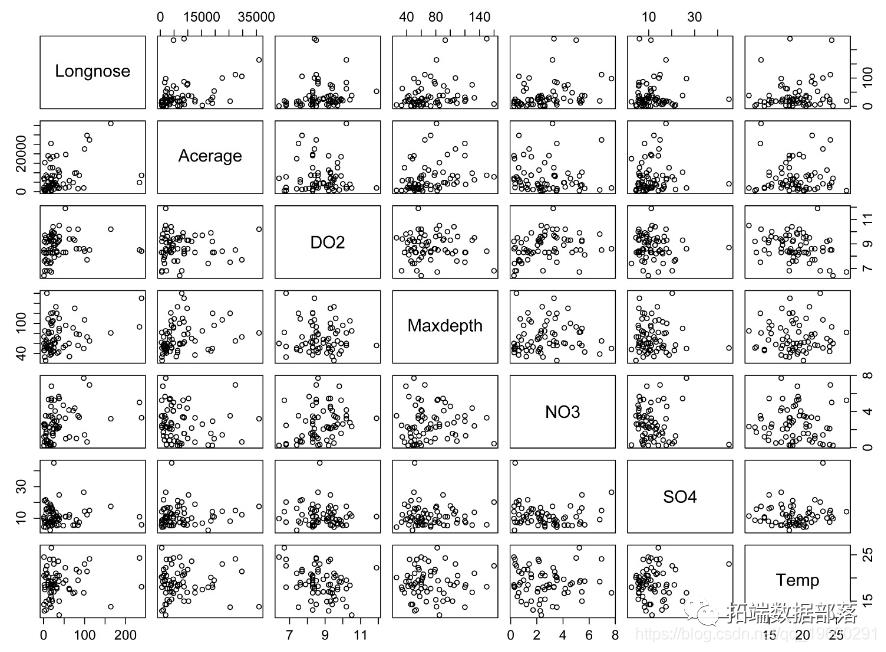
数据集包含多个数值变量时,最好查看这些变量之间的相关性。原因之一是,可以轻松查看哪些自变量与该因变量相关。第二个原因是,如果要构建多元回归模型,则添加高度相关的自变量不太可能对模型有很大的改进。
最后,值得看一下数字变量的分布。如果分布差异很大,则使用Kendall或Spearman相关性可能更合适。同样,如果自变量与因变量的分布不同,则可能需要对自变量进行转换。
Data = read.table(textConnection(Input),header=TRUE)
Data.num =
select(Data,
Longnose,
Acerage,
DO2,
Maxdepth,
NO3,
SO4,
Temp)
headtail(Data.num)
Longnose Acerage DO2 Maxdepth NO3 SO4 Temp
1 13 2528 9.6 80 2.28 16.75 15.3
2 12 3333 8.5 83 5.34 7.74 19.4
3 54 19611 8.3 96 0.99 10.92 19.5
66 20 4106 10.0 96 2.62 5.45 15.4
67 38 10274 9.3 90 5.45 24.76 15.0
68 19 510 6.7 82 5.25 14.19 26.5
corr.test(Data.num,
use = "pairwise",
method="pearson",
adjust="none", # 可以调整p值
alpha=.05)
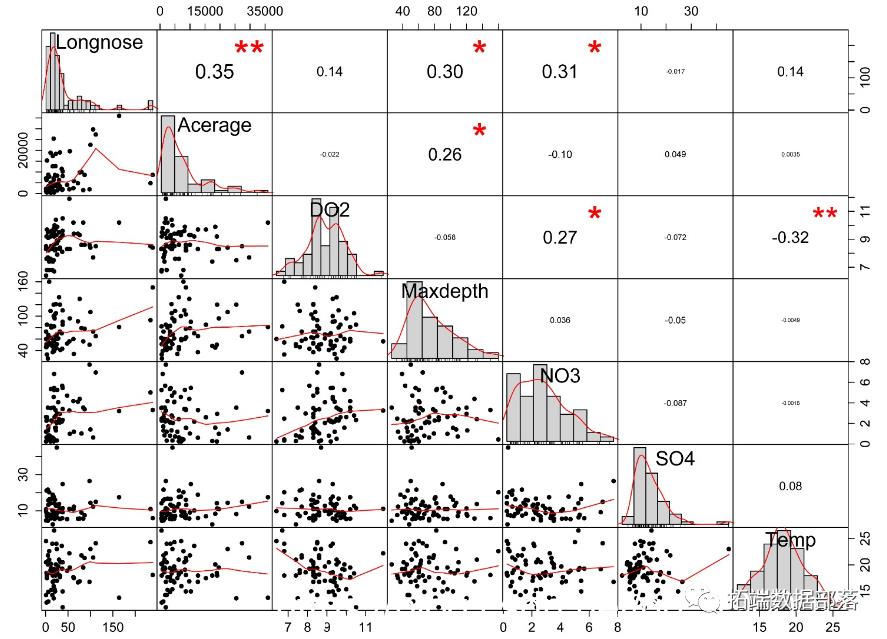
Correlation matrix
Longnose Acerage DO2 Maxdepth NO3 SO4 Temp
Longnose 1.00 0.35 0.14 0.30 0.31 -0.02 0.14
Acerage 0.35 1.00 -0.02 0.26 -0.10 0.05 0.00
DO2 0.14 -0.02 1.00 -0.06 0.27 -0.07 -0.32
Maxdepth 0.30 0.26 -0.06 1.00 0.04 -0.05 0.00
NO3 0.31 -0.10 0.27 0.04 1.00 -0.09 0.00
SO4 -0.02 0.05 -0.07 -0.05 -0.09 1.00 0.08
Temp 0.14 0.00 -0.32 0.00 0.00 0.08 1.00
Sample Size
Probability values (Entries above the diagonal are adjusted for multiple tests.)
Longnose Acerage DO2 Maxdepth NO3 SO4 Temp
Longnose 0.00 0.00 0.27 0.01 0.01 0.89 0.26
Acerage 0.00 0.00 0.86 0.03 0.42 0.69 0.98
DO2 0.27 0.86 0.00 0.64 0.02 0.56 0.01
Maxdepth 0.01 0.03 0.64 0.00 0.77 0.69 0.97
NO3 0.01 0.42 0.02 0.77 0.00 0.48 0.99
SO4 0.89 0.69 0.56 0.69 0.48 0.00 0.52
Temp 0.26 0.98 0.01 0.97 0.99 0.52 0.00
点击标题查阅往期内容

R语言逻辑回归(Logistic Regression)、回归决策树、随机森林信用卡违约分析信贷数据集

左右滑动查看更多

01
02

03

04

逐步回归选择模型
使用AIC(赤池信息标准)作为选择标准。可以使用选项k = log(n) 代替BIC。
逐步程序
Longnose ~ 1
Df Sum of Sq RSS AIC
+ Acerage 1 17989.6 131841 518.75
+ NO3 1 14327.5 135503 520.61
+ Maxdepth 1 13936.1 135894 520.81
<none> 149831 525.45
+ Temp 1 2931.0 146899 526.10
+ DO2 1 2777.7 147053 526.17
+ SO4 1 45.3 149785 527.43
.
.
< snip... more steps >
.
.
Longnose ~ Acerage + NO3 + Maxdepth
Df Sum of Sq RSS AIC
<none> 107904 509.13
+ Temp 1 2948.0 104956 509.24
+ DO2 1 669.6 107234 510.70
- Maxdepth 1 6058.4 113962 510.84
+ SO4 1 5.9 107898 511.12
- Acerage 1 14652.0 122556 515.78
- NO3 1 16489.3 124393 516.80
Call:
lm(formula = Longnose ~ Acerage + NO3 + Maxdepth, data = Data)
Coefficients:
(Intercept) Acerage NO3 Maxdepth
-23.829067 0.001988 8.673044 0.336605
定义最终模型
summary(model.final) # 显示系数,R平方和总体p值
Estimate Std. Error t value Pr(>|t|)
(Intercept) -2.383e+01 1.527e+01 -1.560 0.12367
Acerage 1.988e-03 6.742e-04 2.948 0.00446 **
Maxdepth 3.366e-01 1.776e-01 1.896 0.06253 .
NO3 8.673e+00 2.773e+00 3.127 0.00265 **
Multiple R-squared: 0.2798, Adjusted R-squared: 0.2461
F-statistic: 8.289 on 3 and 64 DF, p-value: 9.717e-05
方差分析
Anova Table (Type II tests)
Response: Longnose
Sum Sq Df F value Pr(>F)
Acerage 14652 1 8.6904 0.004461 **
Maxdepth 6058 1 3.5933 0.062529 .
NO3 16489 1 9.7802 0.002654 **
Residuals 107904 64
预测值图
**
**
检查模型的假设

线性模型中残差的直方图。这些残差的分布应近似正态。

残差与预测值的关系图。残差应无偏且均等。
模型拟合标准
模型拟合标准可用于确定最合适的模型。使用AIC或可选的BIC。AICc是对AIC的一种调整,它更适合于观测值相对较少的数据集。AIC,AICc和BIC越小越好。
在下面的例子中,我们只讨论了显著相关的种植面积,MAXDEPTH和NO3 。
$Models
Formula
1 "Longnose ~ Acerage"
2 "Longnose ~ Maxdepth"
3 "Longnose ~ NO3"
4 "Longnose ~ Acerage + Maxdepth"
5 "Longnose ~ Acerage + NO3"
6 "Longnose ~ Maxdepth + NO3"
7 "Longnose ~ Acerage + Maxdepth + NO3"
8 "Longnose ~ Acerage + Maxdepth + NO3 + DO2"
9 "Longnose ~ Acerage + Maxdepth + NO3 + SO4"
10 "Longnose ~ Acerage + Maxdepth + NO3 + Temp"
$Fit.criteria
Rank Df.res AIC AICc BIC R.squared Adj.R.sq p.value Shapiro.W Shapiro.p
1 2 66 713.7 714.1 720.4 0.12010 0.10670 3.796e-03 0.7278 6.460e-10
2 2 66 715.8 716.2 722.4 0.09301 0.07927 1.144e-02 0.7923 2.115e-08
3 2 66 715.6 716.0 722.2 0.09562 0.08192 1.029e-02 0.7361 9.803e-10
4 3 65 711.8 712.4 720.6 0.16980 0.14420 2.365e-03 0.7934 2.250e-08
5 3 65 705.8 706.5 714.7 0.23940 0.21600 1.373e-04 0.7505 2.055e-09
6 3 65 710.8 711.4 719.6 0.18200 0.15690 1.458e-03 0.8149 8.405e-08
7 4 64 704.1 705.1 715.2 0.27980 0.24610 9.717e-05 0.8108 6.511e-08
8 5 63 705.7 707.1 719.0 0.28430 0.23890 2.643e-04 0.8041 4.283e-08
9 5 63 706.1 707.5 719.4 0.27990 0.23410 3.166e-04 0.8104 6.345e-08
10 5 63 704.2 705.6 717.5 0.29950 0.25500 1.409e-04 0.8225 1.371e-07

几个模型的AICc(修改后的Akaike信息标准)图。模型7最小化了AICc,因此被选为该模型中的最佳模型。
将模型与似然比检验进行比较
将模型与 平方和检验或似然比检验进行比较,以查看是否有其他项显着减少平方误差和 。
Analysis of Variance Table
Model 1: Longnose ~ Acerage + Maxdepth + NO3
Model 2: Longnose ~ Acerage + Maxdepth
Res.Df RSS Df Sum of Sq F Pr(>F)
1 64 107904
2 65 124393 -1 -16489 9.7802 0.002654 **
Likelihood ratio test
Model 1: Longnose ~ Acerage + Maxdepth + NO3
Model 2: Longnose ~ Acerage + Maxdepth
#Df LogLik Df Chisq Pr(>Chisq)
1 5 -347.05
2 4 -351.89 -1 9.6701 0.001873 **
Model 1: Longnose ~ Acerage + Maxdepth + NO3 + DO2
Model 2: Longnose ~ Acerage + Maxdepth + NO3 + SO4
Model 3: Longnose ~ Acerage + Maxdepth + NO3 + Temp
Model A: Longnose ~ Acerage + Maxdepth + NO3
DfO RSSO DfA RSSA Df SS F Pr(>F)
1vA 63 107234.38 64 107903.97 -1 -669.59 0.3934 0.5328
2vA 63 107898.06 64 107903.97 -1 -5.91 0.0035 0.9533
3vA 63 104955.97 64 107903.97 -1 -2948.00 1.7695 0.1882
Model 1: Longnose ~ Acerage + Maxdepth + NO3 + DO2
Model 2: Longnose ~ Acerage + Maxdepth + NO3 + SO4
Model 3: Longnose ~ Acerage + Maxdepth + NO3 + Temp
Model A: Longnose ~ Acerage + Maxdepth + NO3
DfO logLikO DfA logLikA Df logLik Chisq Pr(>Chisq)
1vA 63 -346.83881 64 -347.05045 -1 0.21164 0.4233 0.5153
2vA 63 -347.04859 64 -347.05045 -1 0.00186 0.0037 0.9513
3vA 63 -346.10863 64 -347.05045 -1 0.94182 1.8836 0.1699

点击文末 “阅读原文”
获取全文完整代码数据资料。
本文选自《R语言逐步多元回归模型分析长鼻鱼密度影响因素》。
点击标题查阅往期内容
PYTHON用户流失数据挖掘:建立逻辑回归、XGBOOST、随机森林、决策树、支持向量机、朴素贝叶斯和KMEANS聚类用户画像
Python对商店数据进行lstm和xgboost销售量时间序列建模预测分析
PYTHON集成机器学习:用ADABOOST、决策树、逻辑回归集成模型分类和回归和网格搜索超参数优化
R语言集成模型:提升树boosting、随机森林、约束最小二乘法加权平均模型融合分析时间序列数据
Python对商店数据进行lstm和xgboost销售量时间序列建模预测分析
R语言用主成分PCA、 逻辑回归、决策树、随机森林分析心脏病数据并高维可视化
R语言基于树的方法:决策树,随机森林,Bagging,增强树
R语言用逻辑回归、决策树和随机森林对信贷数据集进行分类预测
spss modeler用决策树神经网络预测ST的股票
R语言中使用线性模型、回归决策树自动组合特征因子水平
R语言中自编基尼系数的CART回归决策树的实现
R语言用rle,svm和rpart决策树进行时间序列预测
python在Scikit-learn中用决策树和随机森林预测NBA获胜者
python中使用scikit-learn和pandas决策树进行iris鸢尾花数据分类建模和交叉验证
R语言里的非线性模型:多项式回归、局部样条、平滑样条、 广义相加模型GAM分析
R语言用标准最小二乘OLS,广义相加模型GAM ,样条函数进行逻辑回归LOGISTIC分类
R语言ISLR工资数据进行多项式回归和样条回归分析
R语言中的多项式回归、局部回归、核平滑和平滑样条回归模型
R语言用泊松Poisson回归、GAM样条曲线模型预测骑自行车者的数量
R语言分位数回归、GAM样条曲线、指数平滑和SARIMA对电力负荷时间序列预测R语言样条曲线、决策树、Adaboost、梯度提升(GBM)算法进行回归、分类和动态可视化
如何用R语言在机器学习中建立集成模型?
R语言ARMA-EGARCH模型、集成预测算法对SPX实际波动率进行预测在python 深度学习Keras中计算神经网络集成模型R语言ARIMA集成模型预测时间序列分析R语言基于Bagging分类的逻辑回归(Logistic Regression)、决策树、森林分析心脏病患者
R语言基于树的方法:决策树,随机森林,Bagging,增强树
R语言基于Bootstrap的线性回归预测置信区间估计方法
R语言使用bootstrap和增量法计算广义线性模型(GLM)预测置信区间
R语言样条曲线、决策树、Adaboost、梯度提升(GBM)算法进行回归、分类和动态可视化
Python对商店数据进行lstm和xgboost销售量时间序列建模预测分析
R语言随机森林RandomForest、逻辑回归Logisitc预测心脏病数据和可视化分析
R语言用主成分PCA、 逻辑回归、决策树、随机森林分析心脏病数据并高维可视化
Matlab建立SVM,KNN和朴素贝叶斯模型分类绘制ROC曲线
matlab使用分位数随机森林(QRF)回归树检测异常值
回归分析 R语言 -- 多元线性回归
参考技术A多元线性回归 是 简单线性回归 的扩展,用于基于多个不同的预测变量(x)预测结果变量(y)。
例如,对于三个预测变量(x),y的预测由以下等式表示: y = b0 + b1*x1 + b2*x2 + b3*x3
回归贝塔系数测量每个预测变量与结果之间的关联。“ b_j”可以解释为“ x_j”每增加一个单位对y的平均影响,同时保持所有其他预测变量不变。
在本节中,依然使用 datarium 包中的 marketing 数据集,我们将建立一个多元回归模型,根据在三种广告媒体(youtube,facebook和报纸)上投入的预算来预测销售。计算公式如下: sales = b0 + b1*youtube + b2*facebook + b3*newspaper
您可以如下计算R中的多个回归模型系数:
请注意,如果您的数据中包含许多预测变量,则可以使用 ~. 以下命令将模型中的所有可用变量简单地包括在内:
从上面的输出中,系数表显示β系数估计值及其显着性水平。列为:
如前所述,您可以使用R函数轻松进行预测 predict() :
在使用模型进行预测之前,您需要评估模型的统计显着性。通过显示模型的统计摘要,可以轻松地进行检查。
显示模型的统计摘要,如下所示:
摘要输出显示6个组件,包括:
解释多元回归分析的第一步是在模型摘要的底部检查F统计量和关联的p值。
在我们的示例中,可以看出F统计量的p值<2.2e-16,这是非常重要的。这意味着 至少一个预测变量与结果变量显着相关 。
要查看哪些预测变量很重要,您可以检查系数表,该表显示了回归beta系数和相关的t统计p值的估计。
对于给定的预测变量,t统计量评估预测变量和结果变量之间是否存在显着关联,即,预测变量的beta系数是否显着不同于零。
可以看出,youtube和facebook广告预算的变化与销售的变化显着相关,而报纸预算的变化与销售却没有显着相关。
对于给定的预测变量,系数(b)可以解释为预测变量增加一个单位,同时保持所有其他预测变量固定的对y的平均影响。
例如,对于固定数量的youtube和报纸广告预算,在Facebook广告上花费额外的1000美元,平均可以使销售额增加大约0.1885 * 1000 = 189个销售单位。
youtube系数表明,在所有其他预测变量保持不变的情况下,youtube广告预算每增加1000美元,我们平均可以预期增加0.045 * 1000 = 45个销售单位。
我们发现报纸在多元回归模型中并不重要。这意味着,对于固定数量的youtube和报纸广告预算,报纸广告预算的变化不会显着影响销售单位。
由于报纸变量不重要,因此可以 将其从模型中删除 ,以提高模型精度:
最后,我们的模型公式可以写成如下:。 sales = 3.43+ 0.045*youtube + 0.187*facebook
一旦确定至少一个预测变量与结果显着相关,就应该通过检查模型对数据的拟合程度来继续诊断。此过程也称为拟合优度
可以使用以下三个数量来评估线性回归拟合的整体质量,这些数量显示在模型摘要中:
与预测误差相对应的RSE(或模型 sigma )大致代表模型观察到的结果值和预测值之间的平均差。RSE越低,模型就越适合我们的数据。
将RSE除以结果变量的平均值将为您提供预测误差率,该误差率应尽可能小。
在我们的示例中,仅使用youtube和facebook预测变量,RSE = 2.11,这意味着观察到的销售值与预测值的平均偏差约为2.11个单位。
这对应于2.11 / mean(train.data $ sales)= 2.11 / 16.77 = 13%的错误率,这很低。
R平方(R2)的范围是0到1,代表结果变量中的变化比例,可以用模型预测变量来解释。
对于简单的线性回归,R2是结果与预测变量之间的皮尔森相关系数的平方。在多元线性回归中,R2表示观察到的结果值与预测值之间的相关系数。
R2衡量模型拟合数据的程度。R2越高,模型越好。然而,R2的一个问题是,即使将更多变量添加到模型中,R2总是会增加,即使这些变量与结果之间的关联性很小(James等,2014)。解决方案是通过考虑预测变量的数量来调整R2。
摘要输出中“已调整的R平方”值中的调整是对预测模型中包含的x变量数量的校正。
因此,您应该主要考虑调整后的R平方,对于更多数量的预测变量,它是受罚的R2。
在我们的示例中,调整后的R2为0.88,这很好。
回想一下,F统计量给出了模型的整体重要性。它评估至少一个预测变量是否具有非零系数。
在简单的线性回归中,此检验并不是真正有趣的事情,因为它只是复制了系数表中可用的t检验给出的信息。
一旦我们开始在多元线性回归中使用多个预测变量,F统计量就变得更加重要。
大的F统计量将对应于统计上显着的p值(p <0.05)。在我们的示例中,F统计量644产生的p值为1.46e-42,这是非常重要的。
我们将使用测试数据进行预测,以评估回归模型的性能。
步骤如下:
从上面的输出中,R2为 0.9281111 ,这意味着观察到的结果值与预测的结果值高度相关,这非常好。
预测误差RMSE为 1.612069 ,表示误差率为 1.612069 / mean(testData $ sales) = 1.612069/ 15.567 = 10.35 % ,这很好。
本章介绍了线性回归的基础,并提供了R中用于计算简单和多个线性回归模型的实例。我们还描述了如何评估模型的性能以进行预测。
以上是关于R语言逐步多元回归模型分析长鼻鱼密度影响因素|附代码数据的主要内容,如果未能解决你的问题,请参考以下文章
R语言Logistic逐步回归模型案例:分析与冠心病有关的危险因素