强化学习python 实现 q-learning 例二
Posted 罗兵の水库
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了强化学习python 实现 q-learning 例二相关的知识，希望对你有一定的参考价值。
本文作者：hhh5460
本文地址：https://www.cnblogs.com/hhh5460/p/10134855.html
问题情境
一个2*2的迷宫，一个入口，一个出口，还有一个陷阱。如图
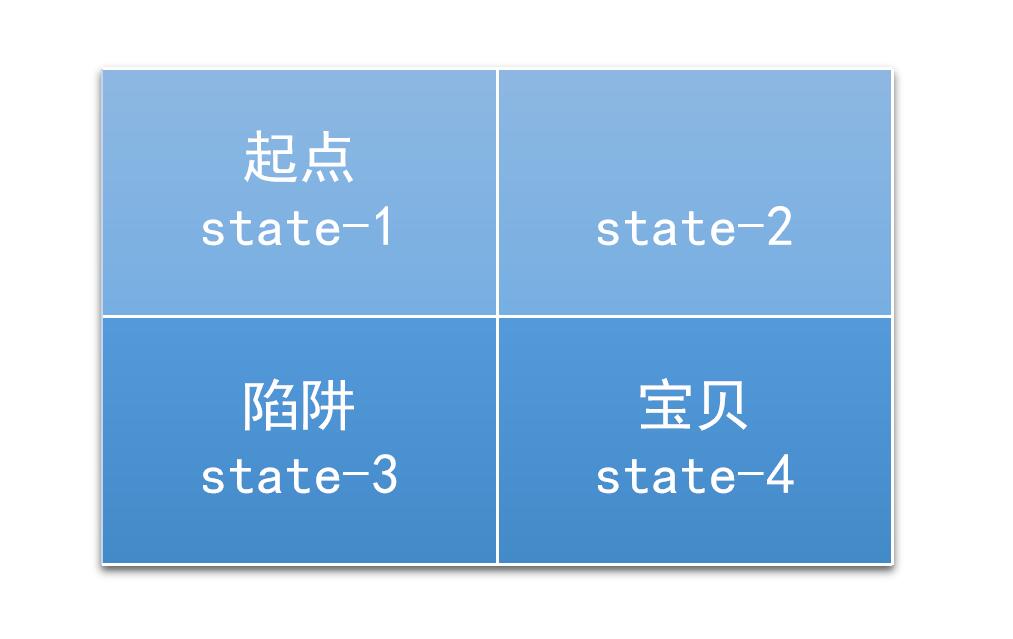（图片来源：https://jizhi.im/blog/post/intro_q_learning）
这是一个二维的问题，不过我们可以把这个降维，变为一维的问题。
感谢：https://jizhi.im/blog/post/intro_q_learning。网上看了无数文章，无数代码，都不得要领！直到看了这篇里面的三个矩阵：reward，transition_matrix，valid_actions才真正理解q-learning算法如何操作，如何实现！
的代码先睹为快，绝对让你秒懂q-learning算法，当然我也做了部分润色：
import numpy as np import random \'\'\' 2*2的迷宫 --------------- | 入口 | | --------------- | 陷阱 | 出口 | --------------- # 来源：https://jizhi.im/blog/post/intro_q_learning 每个格子是一个状态，此时都有上下左右停5个动作 任务：通过学习，找到一条通径 \'\'\' gamma = 0.7 # u, d, l, r, n reward = np.array([( 0, -10, 0, -1, -1), #0，状态0 ( 0, 10, -1, 0, -1), #1 (-1, 0, 0, 10, -1), #2 (-1, 0, -10, 0, 10)],#3 dtype=[(\'u\',float),(\'d\',float),(\'l\',float),(\'r\',float),(\'n\',float)]) q_matrix = np.zeros((4, ), dtype=[(\'u\',float),(\'d\',float),(\'l\',float),(\'r\',float),(\'n\',float)]) transition_matrix = np.array([(-1, 2, -1, 1, 0), # 如 state:0,action:\'d\' --> next_state:2 (-1, 3, 0, -1, 1), ( 0, -1, -1, 3, 2), ( 1, -1, 2, -1, 3)], dtype=[(\'u\',int),(\'d\',int),(\'l\',int),(\'r\',int),(\'n\',int)]) valid_actions = np.array([[\'d\', \'r\', \'n\'], #0，状态0 [\'d\', \'l\', \'n\'], #1 [\'u\', \'r\', \'n\'], #2 [\'u\', \'l\', \'n\']])#3 for i in range(1000): current_state = 0 while current_state != 3: current_action = random.choice(valid_actions[current_state]) # 只有探索，没有利用 next_state = transition_matrix[current_state][current_action] next_reward = reward[current_state][current_action] next_q_values = [q_matrix[next_state][next_action] for next_action in valid_actions[next_state]] #待取最大值 q_matrix[current_state][current_action] = next_reward + gamma * max(next_q_values) # 贝尔曼方程（不完整） current_state = next_state print(\'Final Q-table:\') print(q_matrix)
0.相关参数
epsilon = 0.9 # 贪婪度 greedy alpha = 0.1 # 学习率 gamma = 0.8 # 奖励递减值
1.状态集
探索者的状态，即其可到达的位置，有4个。所以定义
states = range(4) # 状态集，从0到3
那么，在某个状态下执行某个动作之后，到达的下一个状态如何确定呢？
def get_next_state(state, action): \'\'\'对状态执行动作后，得到下一状态\'\'\' #u,d,l,r,n = -2,+2,-1,+1,0 if state % 2 != 1 and action == \'r\': # 除最后一列，皆可向右(+1) next_state = state + 1 elif state % 2 != 0 and action == \'l\': # 除最前一列，皆可向左(-1) next_state = state -1 elif state // 2 != 1 and action == \'d\': # 除最后一行，皆可向下(+2) next_state = state + 2 elif state // 2 != 0 and action == \'u\': # 除最前一行，皆可向上(-2) next_state = state - 2 else: next_state = state return next_state
2.动作集
探索者处于每个状态时，可行的动作，只有上下左右4个。所以定义
actions = [\'u\', \'d\', \'l\', \'r\'] # 动作集。上下左右，也可添加动作\'n\'，表示停留
那么，在某个给定的状态（位置），其所有的合法动作如何确定呢？
def get_valid_actions(state): \'\'\'取当前状态下的合法动作集合，与reward无关！\'\'\' global actions # [\'u\',\'d\',\'l\',\'r\',\'n\'] valid_actions = set(actions) if state % 2 == 1: # 最后一列，则 valid_actions = valid_actions - set([\'r\']) # 去掉向右的动作 if state % 2 == 0: # 最前一列，则 valid_actions = valid_actions - set([\'l\']) # 去掉向左 if state // 2 == 1: # 最后一行，则 valid_actions = valid_actions - set([\'d\']) # 去掉向下 if state // 2 == 0: # 最前一行，则 valid_actions = valid_actions - set([\'u\']) # 去掉向上 return list(valid_actions)
3.奖励集
探索者到达每个状态（位置）时，要有奖励。所以定义
rewards = [0,0,-10,10] # 奖励集。到达位置3（出口）奖励10，位置2（陷阱）奖励-10，其他皆为0
显然，取得某状态state下的奖励就很简单了：rewards[state] 。根据state，按图索骥即可，无需额外定义一个函数。
4.Q table
最重要。Q table是一种记录状态-行为值 (Q value) 的表。常见的q-table都是二维的，基本长下面这样：
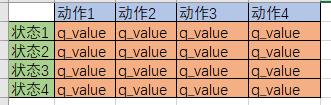（注意，也有3维的Q table）
所以定义
q_table = pd.DataFrame(data=[[0 for _ in actions] for _ in states], index=states, columns=actions)
5.Q-learning算法
Q-learning算法的伪代码
Q value的更新是根据贝尔曼方程：
$$Q(s_t,a_t) \\leftarrow Q(s_t,a_t) + \\alpha[r_{t+1} + \\lambda \\max _{a} Q(s_{t+1}, a) - Q(s_t,a_t)] \\tag {1}$$
好吧，是时候实现它了：
# 总共探索300次 for i in range(300): # 0.从最左边的位置开始（不是必要的） current_state = 0 #current_state = random.choice(states) while current_state != states[-1]: # 1.取当前状态下的合法动作中，随机（或贪婪）地选一个作为 当前动作 if (random.uniform(0,1) > epsilon) or ((q_table.ix[current_state] == 0).all()): # 探索 current_action = random.choice(get_valid_actions(current_state)) else: current_action = q_table.ix[current_state].idxmax() # 利用（贪婪） # 2.执行当前动作，得到下一个状态（位置） next_state = get_next_state(current_state, current_action) # 3.取下一个状态所有的Q value，待取其最大值 next_state_q_values = q_table.ix[next_state, get_valid_actions(next_state)] # 4.根据贝尔曼方程，更新 Q table 中当前状态-动作对应的 Q value q_table.ix[current_state, current_action] += alpha * (rewards[next_state] + gamma * next_state_q_values.max() - q_table.ix[current_state, current_action]) # 5.进入下一个状态（位置） current_state = next_state print(\'\\nq_table:\') print(q_table)
可以看到，与例一的代码一模一样，不差一字！
6.环境及其更新
这里的环境貌似必须用到GUI，有点麻烦；而在命令行下，我又不知如何实现。所以暂时算了，不搞了。
7.完整代码
\'\'\' 最简单的四个格子的迷宫 --------------- | start | | --------------- | die | end | --------------- 每个格子是一个状态，此时都有上下左右4个动作
作者：hhh5460
时间：20181217 \'\'\' import pandas as pd import random epsilon = 0.9 # 贪婪度 greedy alpha = 0.1 # 学习率 gamma = 0.8 # 奖励递减值 states = range(4) # 0, 1, 2, 3 四个状态 actions = list(\'udlr\') # 上下左右 4个动作。还可添加动作\'n\'，表示停留 rewards = [0,0,-10,10] # 奖励集。到达位置3（出口）奖励10，位置2（陷阱）奖励-10，其他皆为0 q_table = pd.DataFrame(data=[[0 for _ in actions] for _ in states], index=states, columns=actions) def get_next_state(state, action): \'\'\'对状态执行动作后，得到下一状态\'\'\' #u,d,l,r,n = -2,+2,-1,+1,0 if state % 2 != 1 and action == \'r\': # 除最后一列，皆可向右(+1) next_state = state + 1 elif state % 2 != 0 and action == \'l\': # 除最前一列，皆可向左(-1) next_state = state -1 elif state // 2 != 1 and action == \'d\': # 除最后一行，皆可向下(+2) next_state = state + 2 elif state // 2 != 0 and action == \'u\': # 除最前一行，皆可向上(-2) next_state = state - 2 else: next_state = state return next_state def get_valid_actions(state): \'\'\'取当前状态下的合法动作集合 global reward valid_actions = reward.ix[state, reward.ix[state]!=0].index return valid_actions \'\'\' # 与reward无关！ global actions valid_actions = set(actions) if state % 2 == 1: # 最后一列，则 valid_actions = valid_actions - set([\'r\']) # 无向右的动作 if state % 2 == 0: # 最前一列，则 valid_actions = valid_actions - set([\'l\']) # 无向左 if state // 2 == 1: # 最后一行，则 valid_actions = valid_actions - set([\'d\']) # 无向下 if state // 2 == 0: # 最前一行，则 valid_actions = valid_actions - set([\'u\']) # 无向上 return list(valid_actions) # 总共探索300次 for i in range(300): # 0.从最左边的位置开始（不是必要的） current_state = 0 #current_state = random.choice(states) while current_state != states[-1]: # 1.取当前状态下的合法动作中，随机（或贪婪）地选一个作为 当前动作 if (random.uniform(0,1) > epsilon) or ((q_table.ix[current_state] == 0).all()): # 探索 current_action = random.choice(get_valid_actions(current_state)) else: current_action = q_table.ix[current_state].idxmax() # 利用（贪婪） # 2.执行当前动作，得到下一个状态（位置） next_state = get_next_state(current_state, current_action) # 3.取下一个状态所有的Q value，待取其最大值 next_state_q_values = q_table.ix[next_state, get_valid_actions(next_state)] # 4.根据贝尔曼方程，更新 Q table 中当前状态-动作对应的 Q value q_table.ix[current_state, current_action] += alpha * (rewards[next_state] + gamma * next_state_q_values.max() - q_table.ix[current_state, current_action]) # 5.进入下一个状态（位置） current_state = next_state print(\'\\nq_table:\') print(q_table)
8.效果图
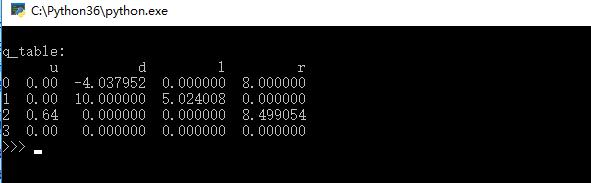
9.补充
又搞了一个numpy版本，比pandas版本的快了一个数量级！！代码如下
\'\'\' 最简单的四个格子的迷宫 --------------- | start | | --------------- | die | end | --------------- 每个格子是一个状态，此时都有上下左右停5个动作 \'\'\' # 作者：hhh5460 # 时间：20181218 import numpy as np epsilon = 0.9 # 贪婪度 greedy alpha = 0.1 # 学习率 gamma = 0.8 # 奖励递减值 states = range(4) # 0, 1, 2, 3 四个状态 actions = list(\'udlrn\') # 上下左右停 五个动作 rewards = [0,0,-10,10] # 奖励集。到达位置3（出口）奖励10，位置2（陷阱）奖励-10，其他皆为0 # 给numpy数组的列加标签，参考https://cloud.tencent.com/developer/ask/72790 q_table = np.zeros(shape=(4, ), # 坑二：这里不能是(4,5)!! dtype=list(zip(actions, [\'float\']*5))) #dtype=[(\'u\',float),(\'d\',float),(\'l\',float),(\'r\',float),(\'n\',float)]) #dtype={\'names\':actions, \'formats\':[float]*5}) def get_next_state(state, action): \'\'\'对状态执行动作后，得到下一状态\'\'\' #u,d,l,r,n = -2,+2,-1,+1,0 if state % 2 != 1 and action == \'r\': # 除最后一列，皆可向右(+1) next_state = state + 1 elif state % 2 != 0 and action == \'l\': # 除最前一列，皆可向左(-1) next_state = state -1 elif state // 2 != 1 and action == \'d\': # 除最后一行，皆可向下(+2) next_state = state + 2 elif state // 2 != 0 and action == \'u\': # 除最前一行，皆可向上(-2) next_state = state - 2 else: next_state = state return next_state def get_valid_actions(state): \'\'\'取当前状态下的合法动作集合，与reward无关！\'\'\' global actions # [\'u\',\'d\',\'l\',\'r\',\'n\'] valid_actions = set(actions) if state % 2 == 1: # 最后一列，则 valid_actions = valid_actions - set([\'r\']) # 去掉向右的动作 if state % 2 == 0: # 最前一列，则 valid_actions = valid_actions - set([\'l\']) # 去掉向左 if state // 2 == 1: # 最后一行，则 valid_actions = valid_actions - set([\'d\']) # 去掉向下 if state // 2 == 0: # 最前一行，则 valid_actions = valid_actions - set([\'u\']) # 去掉向上 return list(valid_actions) for i in range(1000): #current_state = states[0] # 固定 current_state = np.random.choice(states,1)[0] while current_state != 3: if (np.random.uniform() > epsilon) or ((np.array(list(q_table[current_state])) == 0).all()): # q_table[current_state]是numpy.void类型，只能这么操作！！ current_action = np.random.choice(get_valid_actions(current_state), 1)[0] else: current_action = actions[np.array(list(q_table[current_state])).argmax()] # q_table[current_state]是numpy.void类型，只能这么操作！！ next_state = get_next_state(current_state, current_action) next_state_q_values = [q_table[next_state][action] for action in get_valid_actions(next_state)] q_table[current_state][current_action] = rewards[next_state] + gamma * max(next_state_q_values) current_state = next_state print(\'Final Q-table:\') print(q_table)
10.补充2：三维Q table实现！
经过不断的试验，终于撸出了一个三维版的Q table，代码如下！
\'\'\' 最简单的四个格子的迷宫 --------------- | start | | --------------- | die | end | --------------- 每个格子是一个状态，此时都有上下左右停5个动作 \'\'\' \'\'\'三维 Q table 版！！\'\'\' # 作者：hhh5460 # 时间：20181218 import numpy as np import random # np.random.choice不能选二维元素！ epsilon = 0.9 # 贪婪度 greedy alpha = 0.1 # 学习率 gamma = 0.8 # 奖励递减值 states = [(0,0),(0,1),(1,0),(1,1)] #状态集，四个位置 actions = [(-1,0),(1,0),(0,-1),(0,1)] #动作集，上下左右 rewards = [[ 0., 0.], # 奖励集 [-10.,10.]] # q_table是三维的，注意把动作放在了第三维！ # 最里面的[0.,0.,0.,0.]表示某一个状态（格子）对应的四个动作“上下左右”的Q value q_table = np.array([[[0.,0.,0.,0.],[0.,0.,0.,0.]], [[0.,0.,0.,0.],[0.,0.,0.,0.]]]) def get_next_state(state, action): \'\'\'对状态执行动作后，得到下一状态\'\'\' if ((state[1] == 1 and action == (0,1)) or # 最后一列、向右 (state[1] == 0 and action == (0,-1)) or # 最前一列、向左 (state[0] == 1 and action == (1,0)) or # 最后一行、向下 (state[0] == 0 and action == (-1,0))): # 最前一行、向上 next_state = state else: next_state = (state[0] + action[0], state[1] + action[1]) return next_state def get_valid_actions(state): \'\'\'取当前状态下的合法动作集合\'\'\' valid_actions = [] if state[1] < 1: # 除最后一列，可向右 valid_actions.append((0,1)) if state[1] > 0: # 除最前一列，可向左(-1) valid_actions.append((0,-1)) if state[0] < 1: # 除最后一行，可向下 valid_actions.append((1,0)) if state[0] > 0: # 除最前一行，可向上 valid_actions.append((-1,0)) return valid_actions # 总共探索300次 for i in range(1000): # 0.从最左边的位置开始（不是必要的） current_state = (0,0) #current_state = random.choice(states) #current_state = tuple(np.random.randint(2, size=2)) while current_state != states[-1]: # 1.取当前状态下的合法动作中，随机（或贪婪）地选一个作为 当前动作 if (np.random.uniform() > epsilon) or ((q_table[current_state[0],current_state[1]] == 0).all()): # 探索 current_action = random.choice(get_valid_actions(current_state)) else: current_action = actions[q_table[current_state[0],current_state[1]].argmax()] # 利用（贪婪） # 2.执行当前动作，得到下一个状态（位置） next_state = get_next_state(current_state, current_action) # 3.取下一个状态所有的Q value，待取其最大值 next_state_q_values = [q_table[next_state[0],next_state[1],actions.index(action)] for action in get_valid_actions(next_state)] # 4.根据贝尔曼方程，更新 Q table 中当前状态-动作对应的 Q value q_table[current_state[0],current_state[1],actions.index(current_action)] += alpha * (rewards[next_state[0]][next_state[1]] + gamma * max(next_state_q_values) - q_table[current_state[0],current_state[1],actions.index(current_action)]) # 5.进入下一个状态（位置） current_state = next_state print(\'\\nq_table:\') print(q_table)
11.课后思考题
有缘看到此文的朋友，请尝试下实现更大规模的迷宫问题，评论交作业哦。迷宫如下：
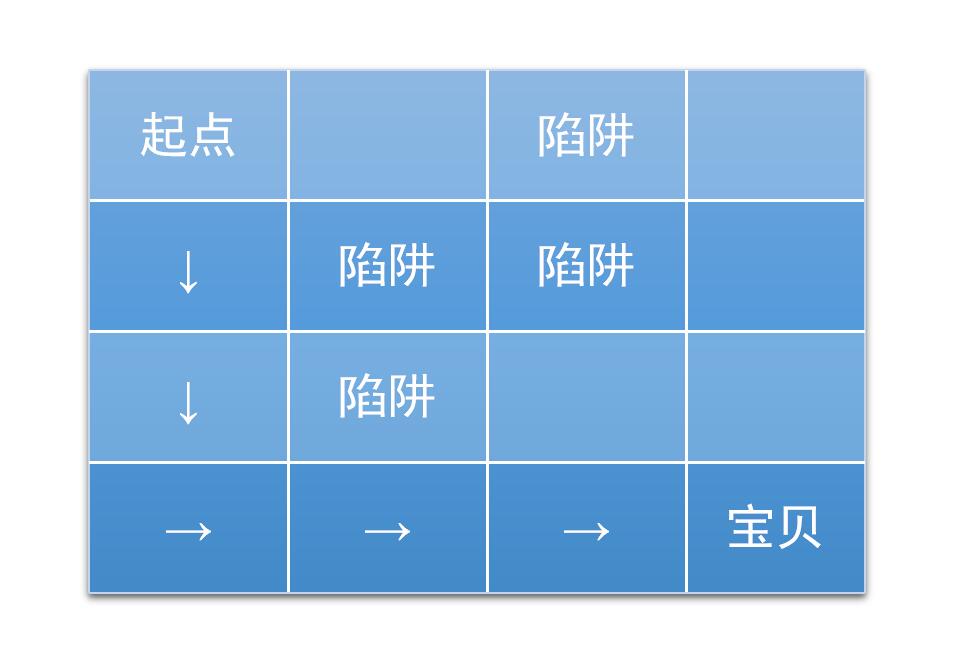（图片来源：https://jizhi.im/blog/post/intro_q_learning）
以上是关于强化学习python 实现 q-learning 例二的主要内容，如果未能解决你的问题，请参考以下文章
强化学习 学习资料汇总强化学习：Q-learning与DQN（Deep Q Network）
强化学习 5 —— SARSA 和 Q-Learning算法代码实现