连续傅里叶变换性质FT
Posted lanlancky
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了连续傅里叶变换性质FT相关的知识,希望对你有一定的参考价值。
常用函数
单位阶跃函数
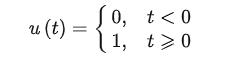
事实上,我们并不怎么关心该函数在x=0 处的值,有的书将其定义为u(0)=1/2 。
其函数图像如下图所示:
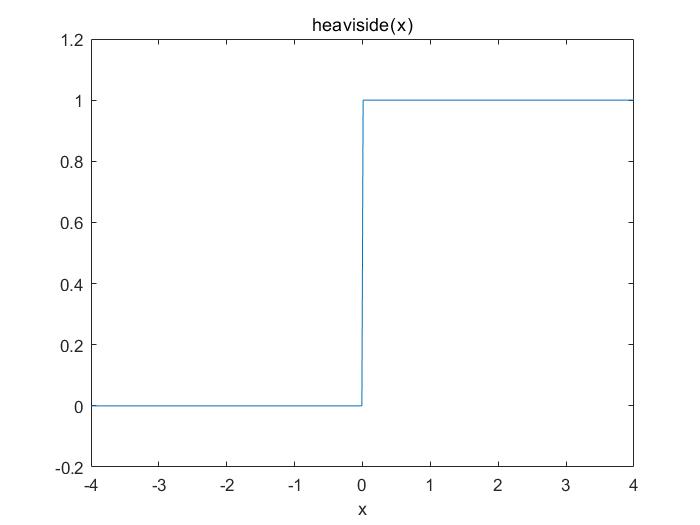
单位冲激函数(δ函数/Dirac函数)
单位冲激函数可以看做
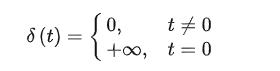
其中有:
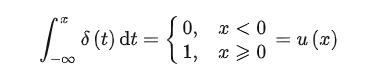
并且有一个被人们称为“筛选性”的性质。顾名思义,对于任意函数f(t),都能筛选出f(t0)的值。
对于δ函数,因为它的取值是0或者无穷,所以我们没办法画出它的图像。我们通常用一个向上的箭头来表示它:
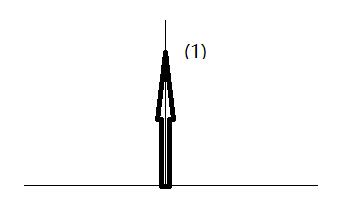
用画图工具大致画了下 关于δ函数具体的形式,有很多种定义方法。例如定义为:
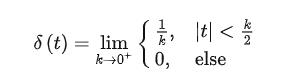
δ函数还有很多性质,如偶函数性和伸缩性质,这些性质结合上式就很容易理解了:
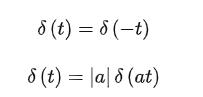
矩形函数(门函数)
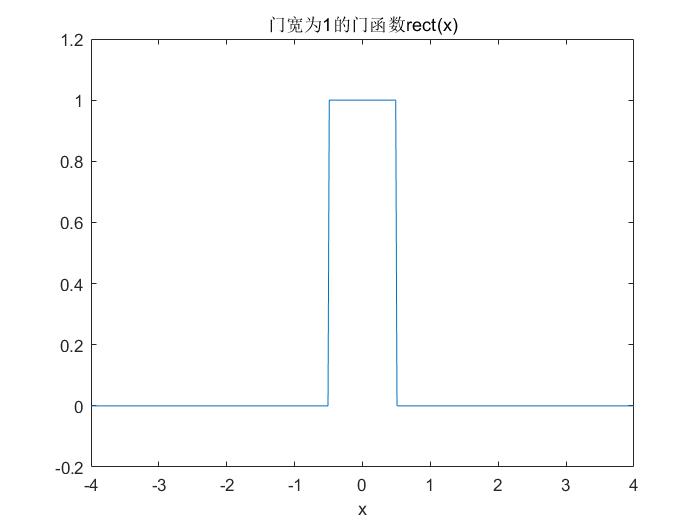
矩形函数的形状类似一扇门,故有时候我们也称之为门函数。将非0区间的长度称为门宽。例如下面就是门宽为1的门函数(矩形函数)的定义:
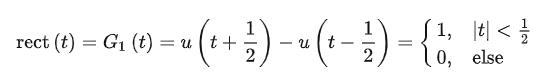
其函数图像如下图所示:
门宽为任意正数 的定义如下:
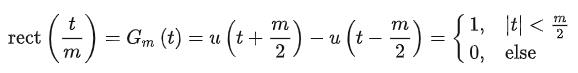
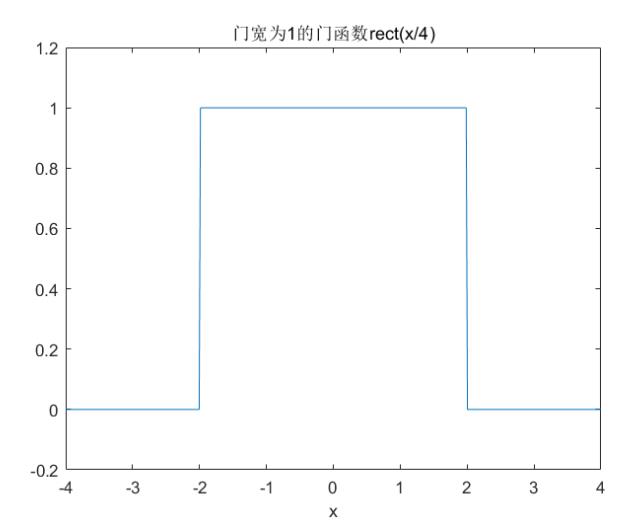
其函数图像如下图所示:
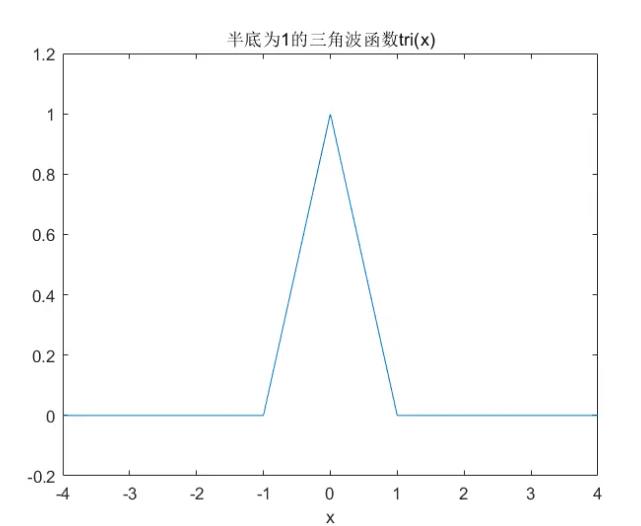
三角波函数
顾名思义,三角波函数就是一个三角形。
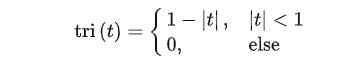
其函数图像如下图所示:
半底宽为任意正数 的定义如下:
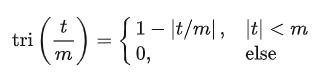
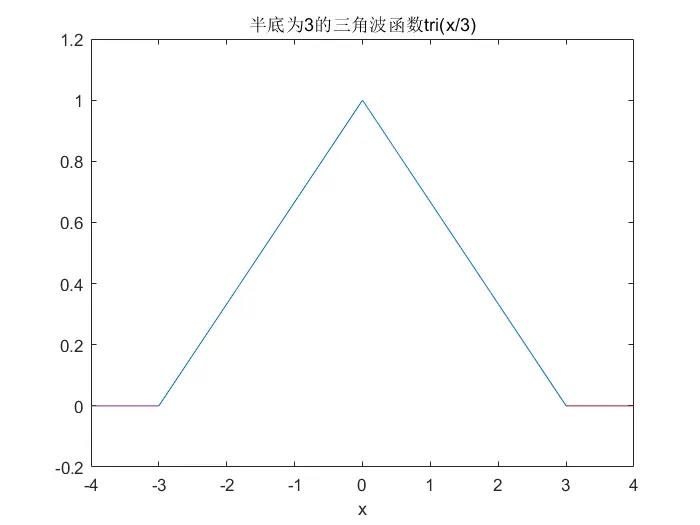
其函数图像如下图所示:
sinc函数
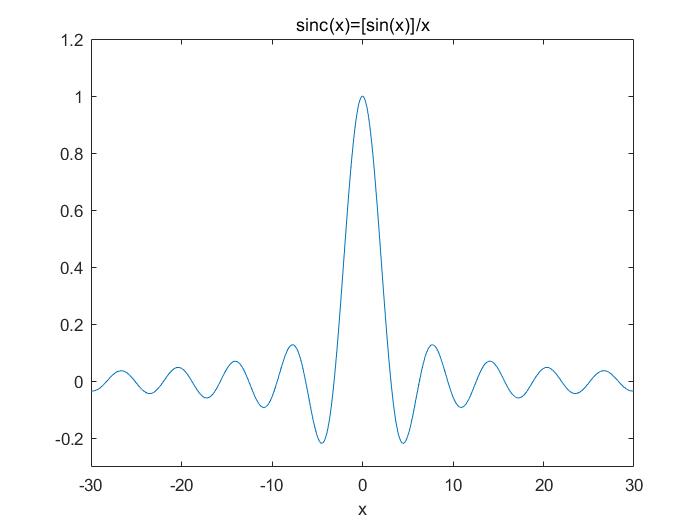
sinc函数在信号处理中十分常用,因为它的傅里叶变换是门函数。在数学系的教材中,它的定义通常乘以了一个系数π。而在我们工科,通常不乘以π。本文采用的是工科的定义,具体定义如下:
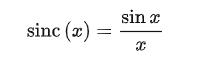
注意到这个函数在x=0处没有定义,但是该点恰好是一个可去间断点,因此将其极限值1作为该点函数值的定义。即sinc(0)=1 。
其函数图像如下图所示:
共轭函数
我们用x*(t) 代表函数x(t) 的共轭函数。
卷积函数
我们用x1(t)*x2(t) 代表x1(t)和x2(t) 的卷积,即:
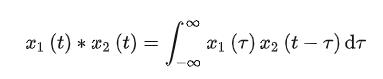
傅里叶变换相关符号的定义
数学系通常用符号i作为虚数单位,而我们工科一般用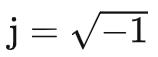 作为虚数单位,本文中所有出现虚数单位的时候都采用j这一符号。并且我们有时候利用关系w=2πf消去逆变换的系数2π。
作为虚数单位,本文中所有出现虚数单位的时候都采用j这一符号。并且我们有时候利用关系w=2πf消去逆变换的系数2π。
我们将自变量为角频率ω的F(w) 函数称为f(t) 的傅里叶变换函数,我们将自变量为频率f的S(f) 函数称为s(t) 的频谱函数。
将傅里叶变换过程用花体符号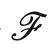 表示:
表示:
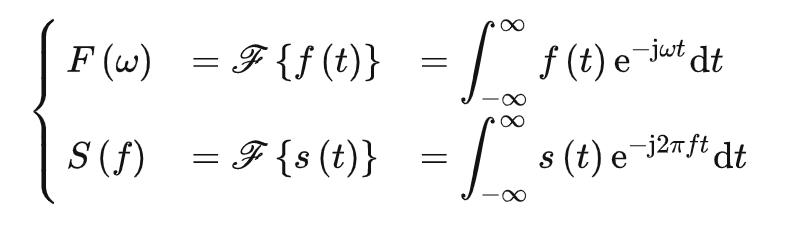
将傅里叶逆变换过程用花体符号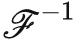 表示:
表示:
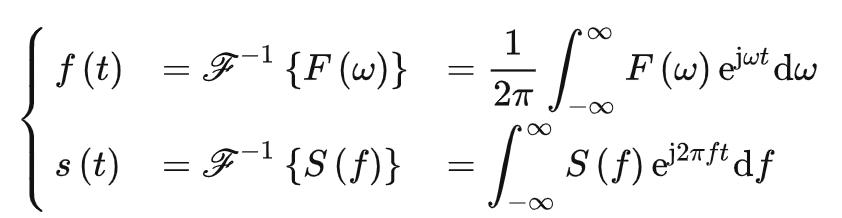
比较明显的是:若s(t)与f(t)相同,则有:
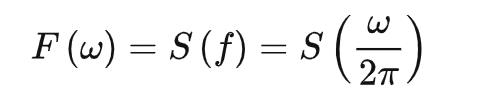
考虑到花体符号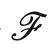 表示对变换关系体现得不是那么显明,因此用下式来表现变换关系会相对更加显明:
表示对变换关系体现得不是那么显明,因此用下式来表现变换关系会相对更加显明:
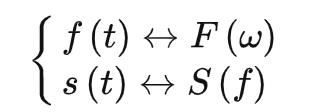
注意:本文中用到a↔b符号时,均指a的傅里叶变换为b。
频域为ω的傅里叶变换性质大全
我们比较常用的是频域为ω的傅里叶变换,不过这样的变换性质会大量出现常数项(2π)。
线性性质
若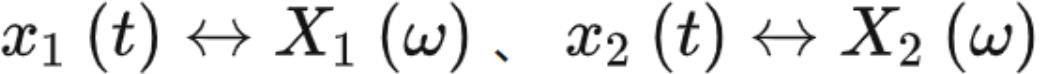 ,a、b为常数,则有:
,a、b为常数,则有:
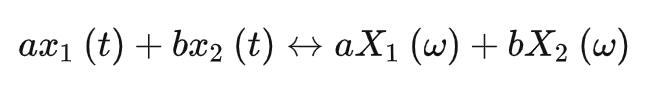
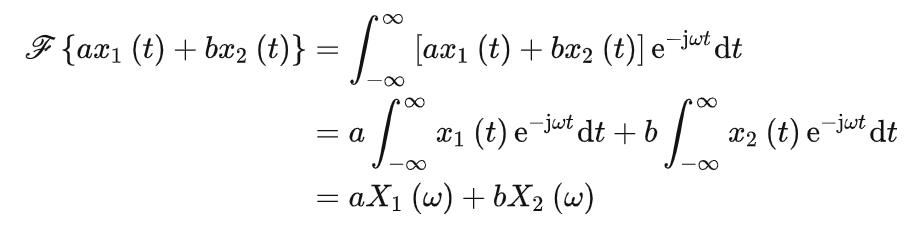
共轭性质
简单地说,实偶对实偶,实奇对虚奇。即:实偶函数的傅里叶变换是实偶函数,实奇函数的傅里叶变换是虚奇函数。
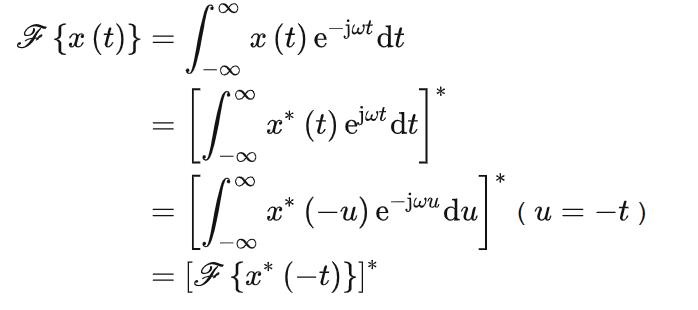
时域平移性
若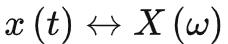 ,则有:
,则有:
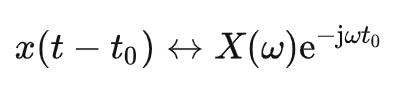
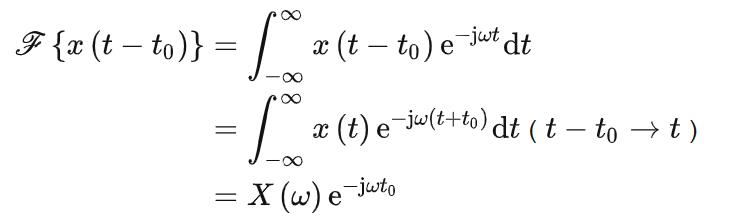
频域平移性
若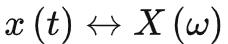 ,则有:
,则有:
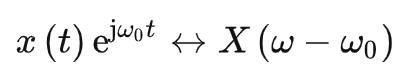
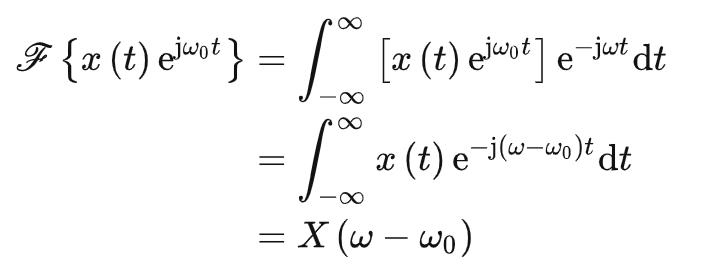
尺度变换性
若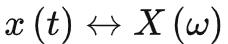 ,对于大于0的常数a,有:
,对于大于0的常数a,有:
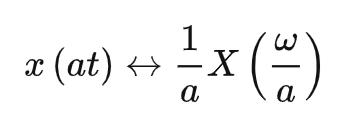
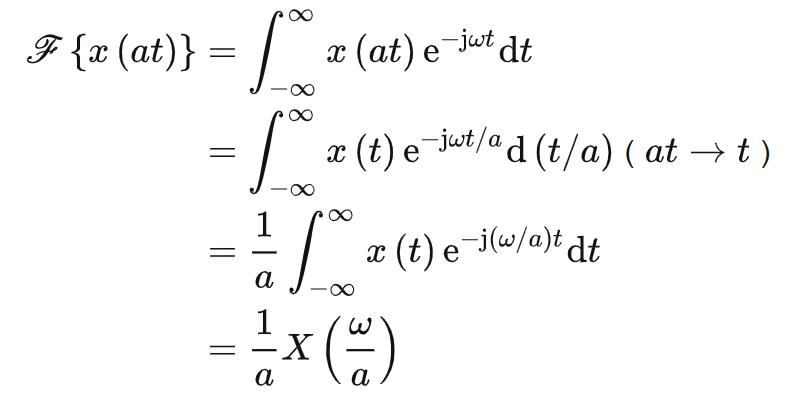
对偶性
若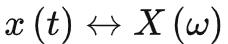 ,有:
,有:
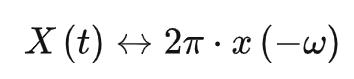
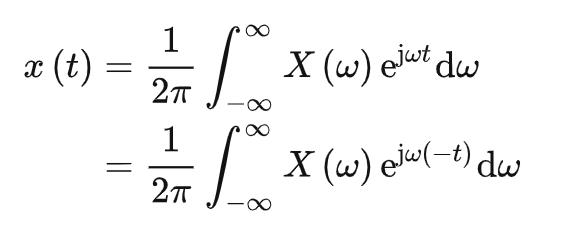
所以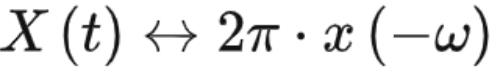 ,将变量名对换即得证。
,将变量名对换即得证。
时域微分性
若 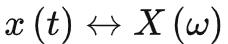 ,有:
,有:
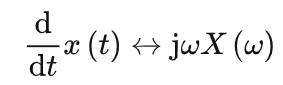
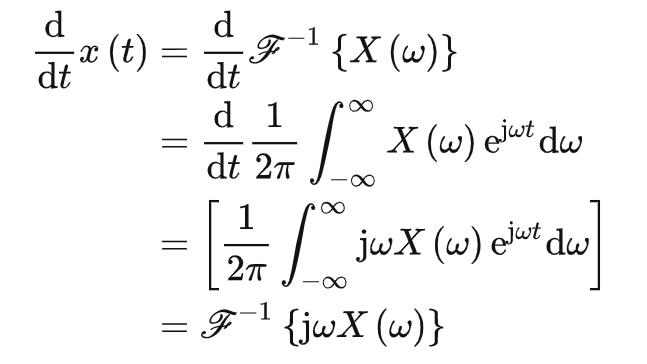
频域微分性
若 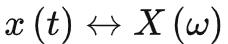 ,有:
,有:
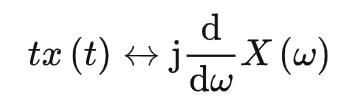
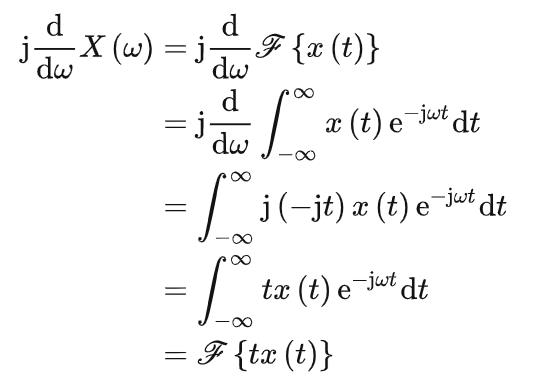
时域积分性
若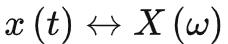 ,有:
,有:
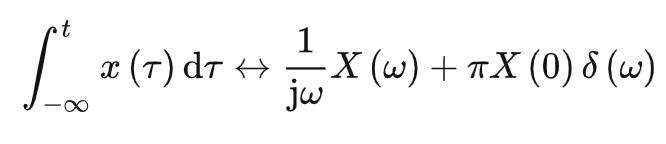
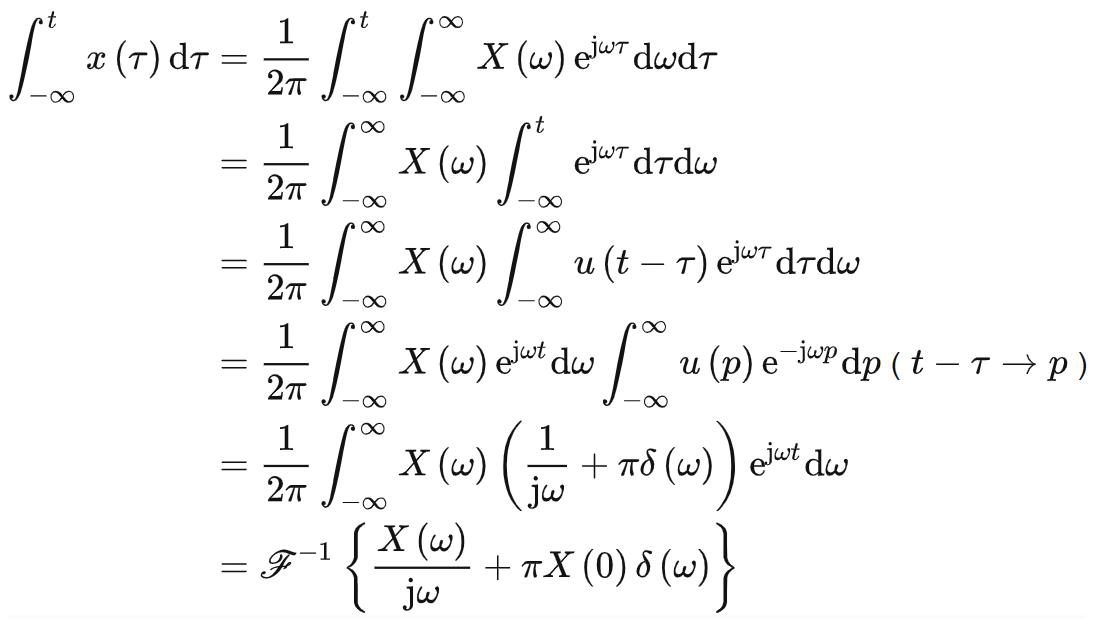
时域卷积
若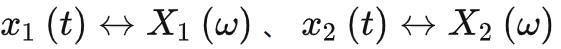 ,有:
,有:
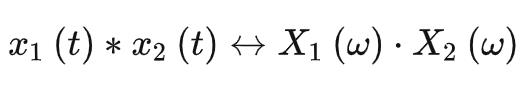
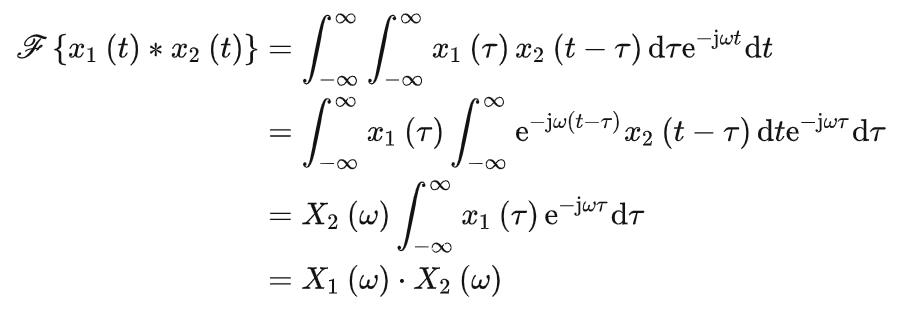
频域卷积
若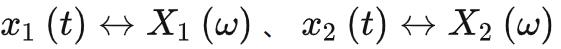 ,有:
,有:
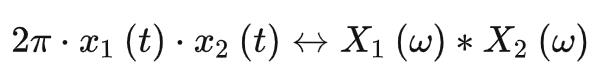
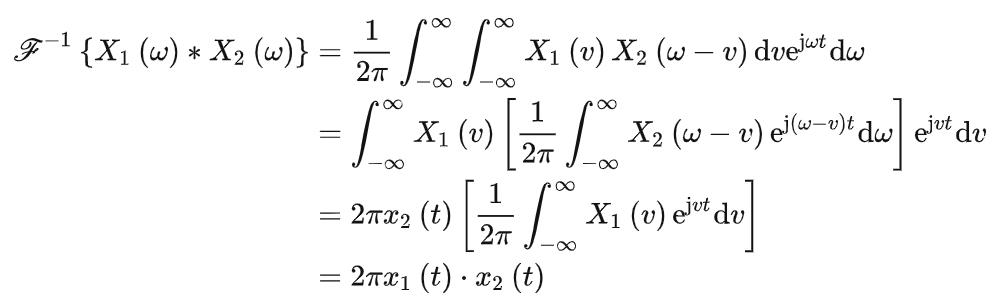
时域初值
若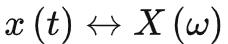 ,有:
,有:
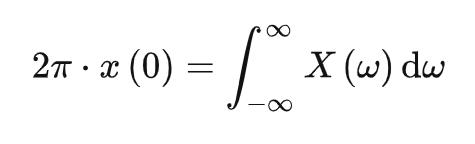
将t=0 代入傅里叶变换的定义:
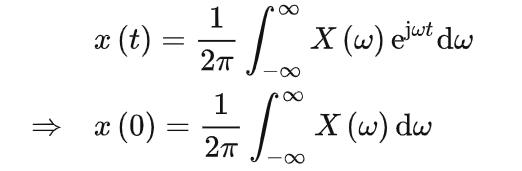
频域初值
若 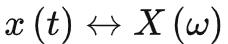 ,有:
,有:
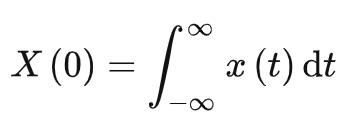
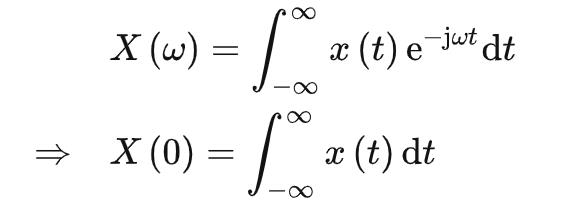
帕塞瓦尔等式
若实函数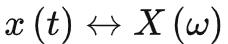 ,有:
,有:
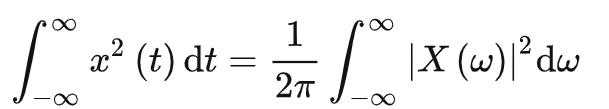
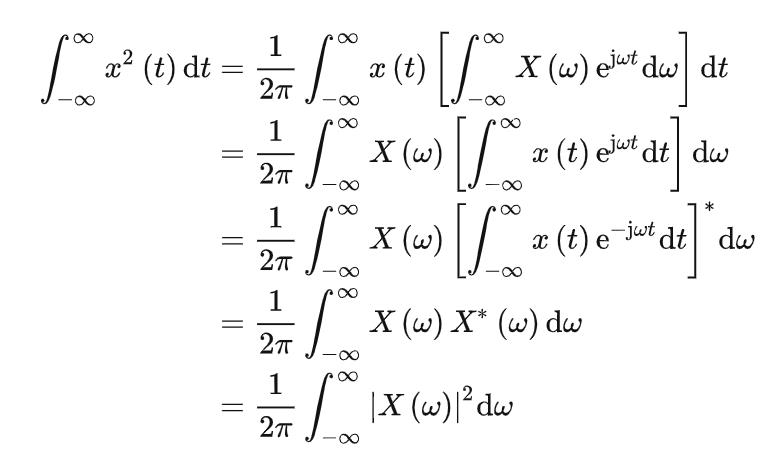
频域为f的傅里叶变换性质大全
对于功率谱的估计,我们有时使用频域为f的傅里叶变换,这样的变换中,一些地方的常数项(2π)会被消掉,因此结果比较简明。
4.1、线性性质
若、 ,a、b为常数,则有:
4.2、共轭性质
简单地说,实偶对实偶,实奇对虚奇。即:实偶函数的傅里叶变换是实偶函数,实奇函数的傅里叶变换是虚奇函数。
4.3、时域平移性
若 则有:
4.4、频域平移性
若 则有:
4.5、尺度变换性
若 ,对于大于0的常数a,有:
4.6、对偶性
若 ,有:
4.7、时域微分性
若 ,有:
4.8、频域微分性
若 ,有:
4.9、时域积分性
若 ,有:
4.10、时域卷积
若 、 ,有:
4.11、频域卷积
若 、 ,有:
4.12、时域初值
若 ,有:
4.13、频域初值
若 ,有:
4.14、帕塞瓦尔等式
若实函数 ,有:
傅里叶对大全
x(t)<->X(f)的变换对根据对偶性很好记。
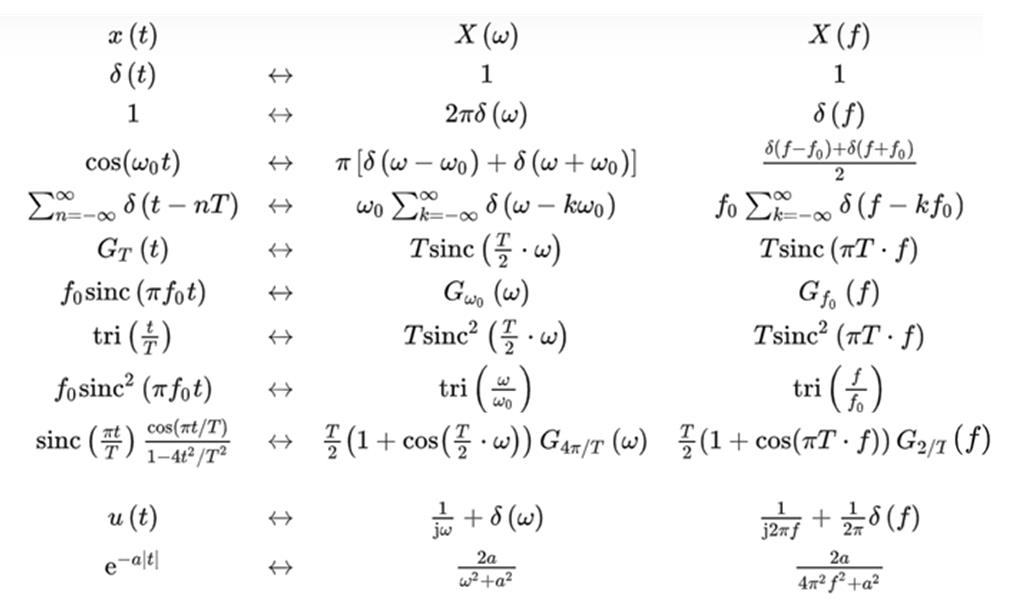
数字信号处理序列傅里叶变换 ( 序列傅里叶变换与反变换 | 序列绝对可和 与 存在傅里叶变换之间的关系 | 序列傅里叶变换性质 )
文章目录
一、序列傅里叶变换与反变换
在上一篇博客 【数字信号处理】序列傅里叶变换 ( 序列傅里叶变换定义详细分析 | 证明单位复指数序列正交完备性 | 序列存在傅里叶变换的性质 | 序列绝对可和 → 序列傅里叶变换一定存在 ) 的介绍了如下内容 :
傅里叶变换 : 时域 " 离散非周期 " 信号 , 其频域就是 " 连续周期 " 的 , 其频域 可以 展开成一个 " 正交函数的无穷级数加权和 " , 如下公式
X ( e j ω ) = ∑ n = − ∞ + ∞ x ( n ) e − j ω n X(e^j\\omega) = \\sum_n=-\\infty^+\\infty x(n) e^-j \\omega n X(ejω)=n=−∞∑+∞x(n)e−jωn
傅里叶反变换 : 利用 " 正交函数 " 可以推导出 " 傅里叶反变换 " , 即 根据 傅里叶变换 推导 序列 ;
x ( n ) = 1 2 π ∫ − π π X ( e j ω ) e j ω k d ω x(n) = \\cfrac12\\pi \\int_-\\pi ^\\pi X( e^j \\omega )e^j \\omega k d \\omega x(n)=2π1∫−ππX(ejω)ejωkdω
二、序列绝对可和 与 存在傅里叶变换之间的关系
序列绝对可和 与 存在傅里叶变换 :
- 如果 " x ( n ) x(n) x(n)序列绝对可和 " , 则 " 序列傅里叶变换 SFT " 一定存在 ;
- 如果 " 序列傅里叶变换 SFT " 存在 , 不一定 " x ( n ) x(n) x(n)序列绝对可和 " ; 某些 " 非绝对可和序列 " , 引入 广义函数 δ ( ω ) \\delta(\\omega) δ(ω) 后 , 其 傅里叶变换也存在 ;
序列绝对可和可以表示成 :
∑ n = − ∞ + ∞ ∣ x ( n ) ∣ < ∞ \\sum_n=-\\infty^+\\infty|x(n)| < \\infty n=−∞∑+∞∣x(n)∣<∞
三、序列傅里叶变换性质
x ( n ) x(n) x(n) 的傅里叶变换是 X ( e j ω ) X(e^j\\omega) X(ejω) , 有如下性质 :
-
连续性 : 序列 x ( n ) x(n) x(n) 是离散的 , 其 傅里叶变换 X ( e j ω ) X(e^j\\omega) X(ejω) 对 ω \\omega ω 来说是连续的 ;
-
周期性 : X ( e j ω ) X(e^j\\omega) X(ejω) 是周期的 , 其周期是 2 π 2\\pi 2π , 其主值区间为 [ − π , π ] [- \\pi , \\pi] [−π,π] ;
X ( e j ω ) = X ( e j ( ω + 2 M π ) ) X(e^j\\omega) = X(e^j( \\omega + 2M\\pi )) X(ejω)=X(ej(ω+2Mπ))
其中 M M M 是整数 ; e − j ω n e^-j\\omega n e−jωn , 将 ω = 2 π M \\omega = 2\\pi M ω=2πM 带入即可得到其是以 2 π 2\\pi 2π 为周期的 ;
- 周期独立性 : 在 相同周期 内的 各个频率 彼此独立 , 频率列举 :
- 数字角频率域 , 即 ω \\omega ω 域
- 直流分量角频率 在 ω = 2 M π \\omega = 2M\\pi ω=2Mπ , π \\pi π 的偶数被上 ;
- 信号 最高角频率 在 ω = ( 2 M + 1 ) π \\omega = (2M + 1 )\\pi ω=(2M+1)π , π \\pi π 的奇数倍 上 ;
数字角频率 ω \\omega ω , 与 模拟角频率 Ω \\Omega Ω 之间的关系 :
ω = Ω T \\omega = \\Omega T ω=ΩT
直流就是 ω = 2 π f \\omega = 2 \\pi f ω=2πf 中的 数字频率 f = 0 f = 0 f=0 ;
直流的时候 , 数字频率 f f f 为 0 0 0 , 则数字角频率 ω \\omega ω 也为 0 0 0 ;
证明 " 直流分量角频率 在 ω = 2 M π \\omega = 2M\\pi ω=2Mπ " :
直流分量 角频率 在 π \\pi π 的偶数倍上 , 角频率 是以 2 π 2\\pi 2π 为周期的 , 周期信号的 组织是 [ − π , π ] [-\\pi , \\pi] [−π,π] ,
在 横轴为 ω \\omega ω 角频率 , 纵轴为 X ( e j ω ) X(e^j\\omega) X(ejω) 的坐标系中 , 横坐标 ω = 0 \\omega = 0 ω=0 位置的值对应 ω = 2 π \\omega = 2 \\pi ω=2π 和 ω = − 2 π \\omega = -2\\pi ω=−2π , 这 3 3 3 个横坐标位置的纵坐标值相等 , 直流分量 永远在 π \\pi π 的偶数倍上 ;
证明 " 最高频率分量 在 π \\pi π 的奇数倍上 " :
根据 ω = Ω T \\omega = \\Omega T ω=ΩT , 计算 ω = π \\omega =\\pi ω=π 点对应的 模拟频率 ,
ω = Ω T = π \\omega = \\Omega T = \\pi ω=ΩT=π
模拟角频率 Ω = π T \\Omega = \\cfrac\\piT Ω=Tπ , 其中 T T T 是采样周期 , 单位是秒 ;
则采样率 F s = 1 T F_s = \\cfrac1T Fs=T1 , 单位是 H z Hz Hz , 每秒采集多少样本 ;
Ω = π T = Ω s 2 \\Omega = \\cfrac\\piT = \\cfrac\\Omega_s2 Ω=Tπ=2Ωs , 其中 Ω s \\Omega_s Ωs 是采样角频率 ;
模拟角频率是 Ω = 2 π f \\Omega = 2\\pi f Ω=2πf , 其中 Ω \\Omega Ω 是模拟角频率 , f f f 是模拟频率 ;
Ω s = 2 π F s = 2 π T \\Omega_s = 2\\pi F_s = \\cfrac2\\piT Ωs=2πFs=T2π
根据采样定理 ,
Ω
s
以上是关于连续傅里叶变换性质FT的主要内容,如果未能解决你的问题,请参考以下文章