斐波那契数列

Posted 2023-05-16 luoqingci

一、问题描述。

题目
求斐波那契数列的40个数，并输出

要求：用for循环来遍历所有可能的选项
二、设计思路。

fibonacci数列可以通过多种方式进行输出，其通项公式为 F（n）=F（n-1）+F（n-2）

基本的for循环、数组再到递归，都可以实现。
题目要求使用for循环，求前40项
第一项和第二项都是1，我们可以用a，b分别代表前两项，f代表第三项，用窗的方式一步一步向后移动。
第一步：a=1，b=1
第二步：f=a+b
第三步：让a=b ，b=f，方便下一次计算

三、代码实现。

 

public class Test
public static int fib(int n)
if(n == 1 || n == 2)
return 1;
else
int a = 1;
int b = 1;
int s = 0;
for(int i = 2;i<n;i++)
s = a + b;
a = b;
b = s;

return s;


public static void main (String[] args)
int result = fib(5);
System.out.println(result);

 

迭代算法

#include <stdio.h>
 
int fib(int n)

int a = 1;
int b = 1;
int c = 0;
while (n >= 3)

c = a + b;
a = b;
b = c;
n--;

return c;

 
int main()

int n = 0;
scanf("%d", &n);
int ret = fib(n);
printf("%d\\n", ret);
return 0;

 

斐波那契数列求和公式

1、奇数项求和

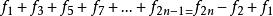
2、偶数项求和

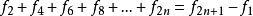
3、平方求和

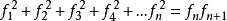
在数学上，斐波那契数列以如下被以递推的方法定义：F(1)=1，F(2)=1, F(n)=F(n-1)+F(n-2)（n>=3，n∈N*）在现代物理、准晶体结构、化学等领域，斐波纳契数列都有直接的应用。

为此，美国数学会从1963年起出版了以《斐波纳契数列季刊》为名的一份数学杂志，用于专门刊载这方面的研究成果。

扩展资料：

斐波那契数列的应用：

1、生物应用

斐波那契数还可以在植物的叶、枝、茎等排列中发现。例如，如果选择树干上的一片叶子，将其计数为零，然后按顺序（假设没有损坏）计数叶子，直到达到适合这些叶子的位置，它们之间的叶子数基本上是斐波那契数。从一个位置移动到下一个位置的叶子称为周期。

叶子在一个周期内旋转的圈数也是斐波那契数。一个循环中叶数与叶旋转圈数之比称为叶序比（源自希腊语，意为叶的排列）。大多数叶序比是斐波那契数。

2、自然界中的应用

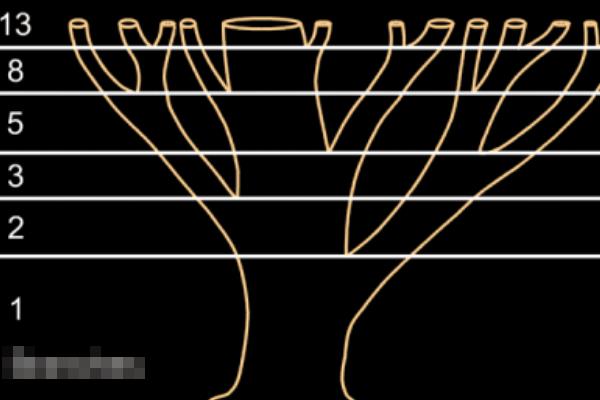
自然界中的斐波那契数列斐波那契数列在自然科学的其他分支，有许多应用。例如，树木的生长，由于新的枝条，往往需要一段时间的“休息”时间来自己生长，才能使新的枝条发芽。因此，例如，幼苗每隔一年生长一个新的枝条。

第二年，新树枝“休息”，老树枝仍在发芽。之后，老枝和老枝“休憩”一年的同时发芽，而当年的新枝则在第二年“休息”。这样，一棵树每年的分枝数就构成了斐波那契数列。这个定律是生物学中著名的“鲁德维格定律”。

参考资料来源：百度百科-斐波那契数列

参考资料来源：百度百科-斐波那契数

参考技术A 斐波那契数列
的
通项公式
为
an=√5/5[(1+√5)/2]^n-√5/5[(1-√5)/2]^n，设bn=√5/5[(1+√5)/2]^n，cn=√5/5[(1-√5)/2]^n
则an=bn-cn，bn是
公比
为(1+√5)/2的
等比数列
，cn是公比为(1-√5)/2的等比数列，
bn的前n项和Bn=√5/5[(1+√5)/2]*(1-[(1+√5)/2]^n)/(1-[(1+√5)/2])
=(3√5+5)([(1+√5)/2]^n-1)/10
cn的前n项和Cn=√5/5[(1-√5)/2]*(1-[(1-√5)/2]^n)/(1-[(1-√5)/2])
=(3√5-5)([(1-√5)/2]^n-1)/10
所以an的前n项和An=a1+a2+…+an=b1-c1+b2-c2+…+bn-cn=Bn-Cn
=(3√5+5)([(1+√5)/2]^n-1)/10-(3√5-5)([(1-√5)/2]^n-1)/10
=(3√5+5)([(1+√5)/2]^n-1)-(3√5-5)([(1-√5)/2]^n-1)/10 参考技术B 利用特征方程的办法（这个请自行参阅组合数学相关的书）。

设斐波那契数列的通项为An。
（事实上An = (p^n - q^n)/√5，其中p = (√5 - 1)/2, q = (√5 + 1)/2。但这里不必解它）

然后记
Sn = A1 + A2 + ... + An
由于
An = Sn - S(n-1) = A(n-1) + A(n-2) = S(n-1) - S(n-2) + S(n-2) - S(n-3)
= S(n-1) - S(n-3)
其中初值为S1 = 1, S2 = 2, S3 = 4。

所以
Sn - 2S(n-1) + S(n-3) = 0
从而其特征方程是
x^3 - 2x^2 + 1 = 0
即
(x - 1)(x^2 - x - 1) = 0
不难解这个三次方程得
x1 = 1
x2 = p
x3 = q
（p, q值同An中的p, q）。
所以通解是
Sn = c1 * x1^n + c2 * x2^n + c3 * x3^n
其中c1，c2，c3的值由S1，S2，S3的三个初值代入上式确定。我就不算了。本回答被提问者采纳 参考技术C 并不是所有的数列都可以求。
但是Fibanocci数列是可以求通项公式的。
a(n+2)=a(n+1)+an
如果能做到：
a(n+2)-ka(n+1)=q(a(n+1)-kan)就好办了。
这应该没问题的，待定系数求k,q. 参考技术D 挺复杂的一个式子，使用积分简单计算出来。

这里也说不清楚，唉……