算法python实现二叉搜索树插入删除查找

Posted 2021-01-19 La La Land

二叉搜索树

 

定义：如果一颗二叉树的每个节点对应一个关键码值，且关键码值的组织是有顺序的，例如左子节点值小于父节点值，父节点值小于右子节点值，则这棵二叉树是一棵二叉搜索树。

 

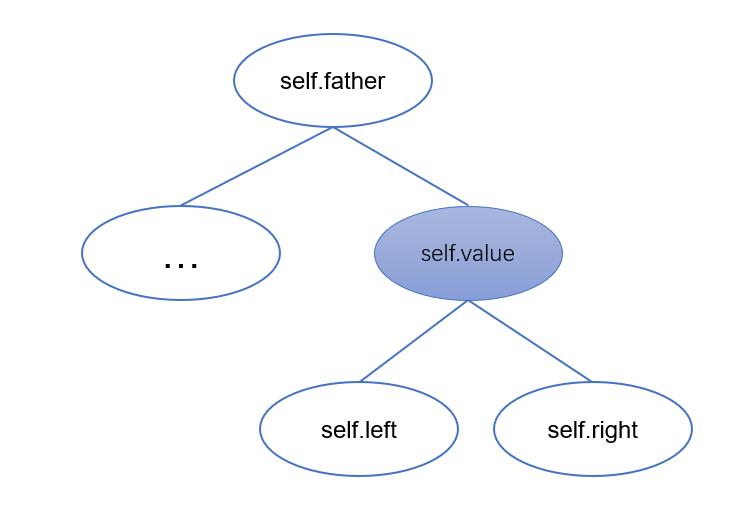
类（TreeNode）：定义二叉搜索树各个节点

在该类中，分别存放节点本身的值，以及其左子节点，右子节点，父节点的值。

 

class TreeNode(object):
    def __init__(self,val):
        self.value = val    #存值
        self.left = None    #存本节点的左子节点
        self.right = None   #存本节点的右子节点
        self.father = None  #存本节点的父节点

　　

类（BST）：定义二叉搜索树的各种功能方法

此类用于存放定义二叉树的插入，删除，搜索等方法。

class BST(object):
    def __init__(self,nodeList):
        self.root = None
        for node in nodeList:
            self.bfs_insert(node)

注：self.bfs_insert(node)中的bfs_insert方法在后面实现。放在构造函数中的目的是将一个列表生成一个二叉搜索树列表。

 

方法（bfs_insert）：实现插入功能

 第一步：将根节点（self.root）设置成当前位置节点（cur），即从根节点开始遍历。根节点的父节点（father）初始设置为None。 

 

def bfs_insert(self,node):
    cur = self.root      #设置当前节点为根节点
    father = None        #设置根节点的父节点为None

　　

第二步：查找可以插入的位置

 

1. 当前位置节点（cur）的值与待插入节点（node）的值相等，返回-1（代表无法进行插入操作）。并将父节点（father）值修改为当前位置节点（cur），代表该节点已经遍历完成。

 

if cur.value == node.value:
    return -1
father = cur

　　

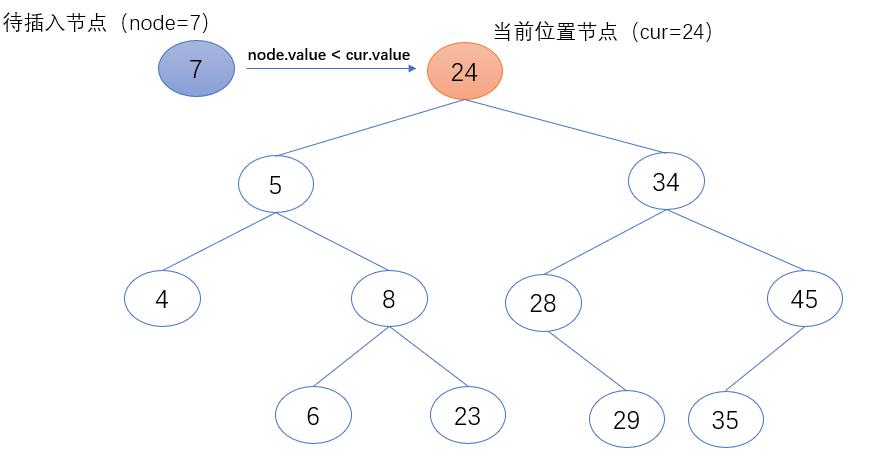
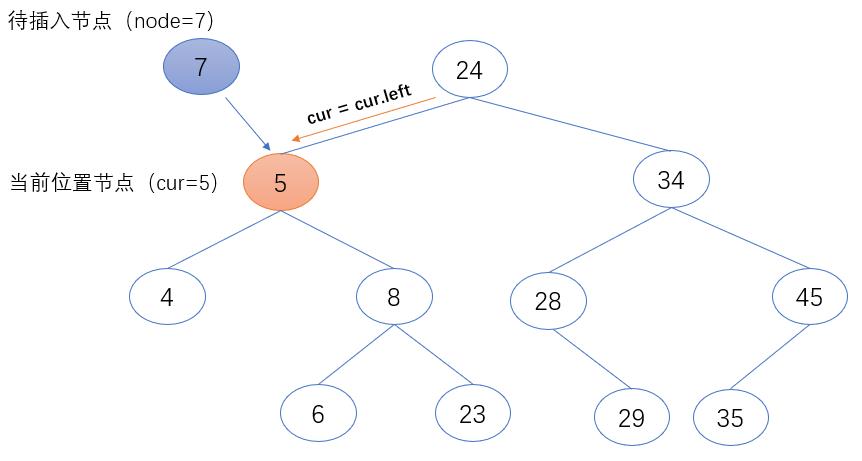
2.当前位置节点（cur）的值大于待插入节点（node）的值时，表示待插入节点（node）需继续在当前位置节点的左子树中继续查找。故把当前位置节点（cur）的左节点赋值给当前位置节点（cur），作为下一个要访问的节点对象。

 

if node.value < cur.value:
    cur = cur.left

　　

 

 

 

 

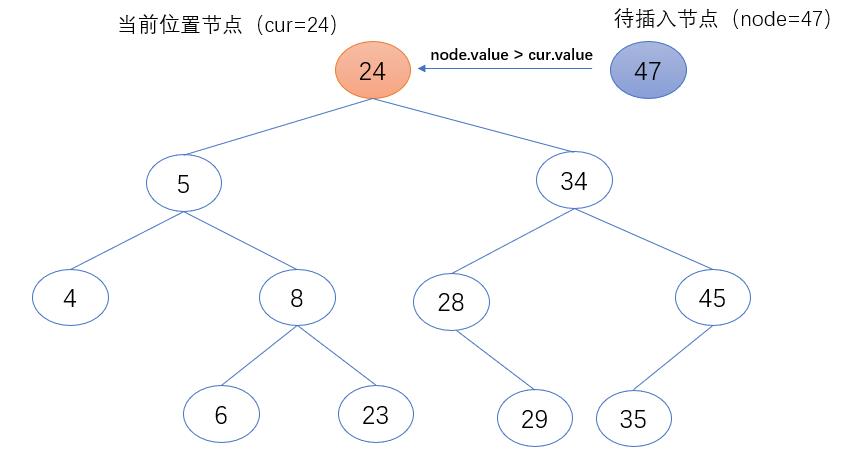
3.当前位置节点（cur）的值小于待插入节点（node）的值时，表示待插入节点（node）需继续在当前位置节点的右子树中继续查找。故把当前位置节点（cur）的右节点赋值给当前位置节点（cur），作为下一个要访问的节点对象。

 

if node.value > cur.value:
    cur = cur.right

　　

 

 

 

 

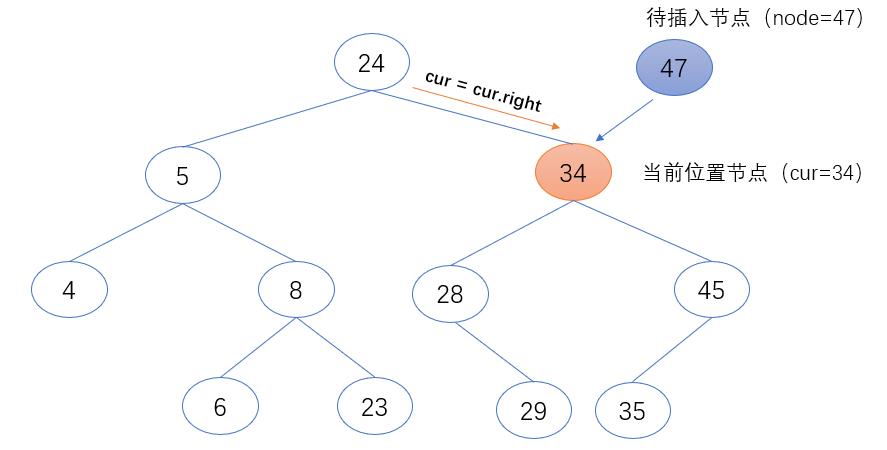
第三步：找到插入位置后，将其设置为待插入值（node）的父节点

 

node.father = father

　　

第四步：插入操作

 

1.父节点的值为空（即要插入的是个空二叉树），将待插入节点（node）赋值给根节点（root）。

 

if father == None:
    self.root = node

　　

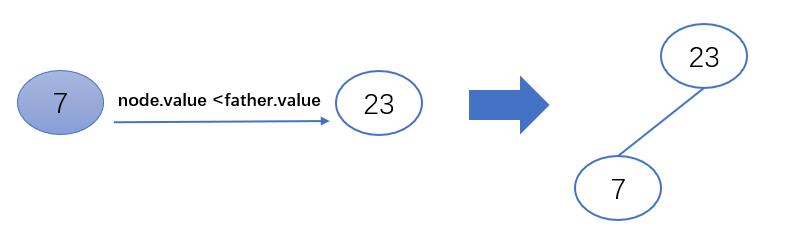
2.待插入节点（node）的值小于父节点（father）的值，将其放到父节点的左子节点

 

if node.value <father.value:
    father.left = node

　

 

 

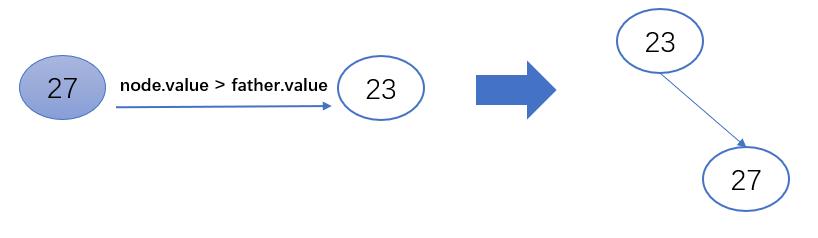
3.待插入节点（node）的值大于父节点（father）的值，将其放到父节点的右子节点

 

if node.value >father.value:
    father.right = node

 

 

插入功能代码汇总：

def insert(self,node):
    father = None
    cur = self.root

    while cur != None:
         if cur.value == node.value:
         	return -1
         father = cur
         if node.value < cur.value:
         	cur = cur.left
         else:
         	cur = cur.right
    node.father = father
    if father == None:
        self.root = node
    elif node.value < father.value:
        father.left = node
    else:
        father.right = node

　　

 

方法（bfs）：生成二叉搜索树列表

利用队列先进先出的特性，将一个二叉搜索树存放到列表中。

 

def bfs(self):
    if self.root == None:
        return None
    retList = []
    q = queue.Queue()
    q.put(self.root)                
    while q.empty() is not True:
        node = q.get()
        retList.append(node.value)
        if node.left != None:
            q.put(node.left)
        if node.right != None:
            q.put(node.right)
    return retList

 

示例：针对如下二叉搜索树，遍历存放到一个列表过程

 

 

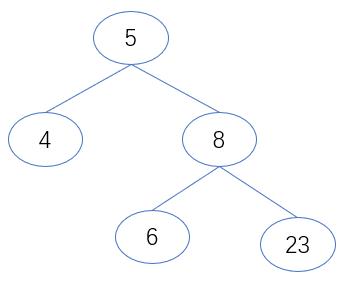
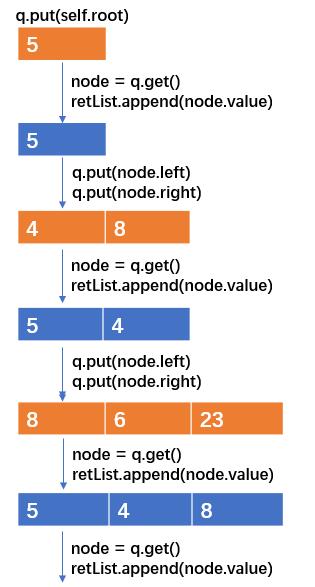
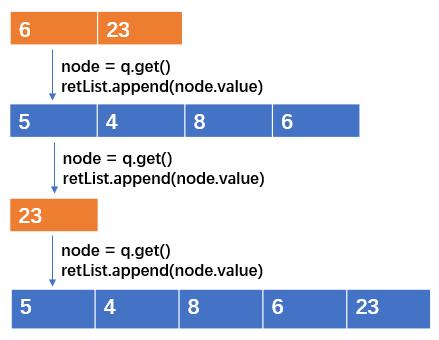
ps：蓝色：二叉树列表 retList    橙色：队列 q

 

方法（bfs_search）：实现查找功能

第一步：将根节点（self.root）设置成当前位置节点（cur），即从根节点开始遍历。

 

def search(self,value):
    cur = self.root

 

如果cur值不为None，执行第二步。否则执行第三步

 

第二步：对比要查找的值（value）与当前位置节点（cur）的值的大小

 

1. 如果当前位置节点（cur）的值等于要查找的值（value），返回当前位置节点（cur）。

 

if cur.value == value:
    return cur

 

 

 

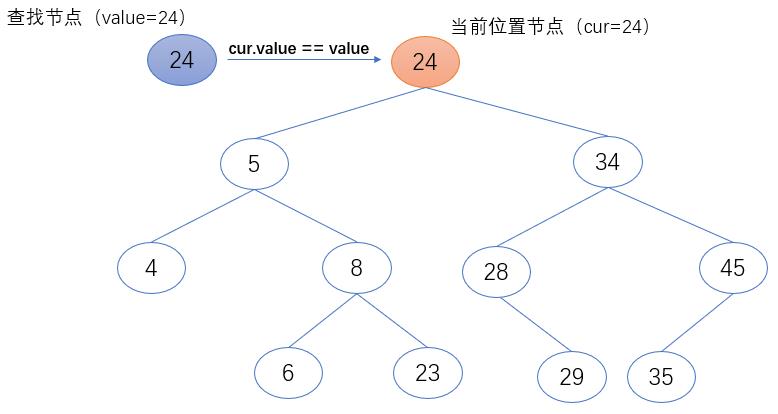
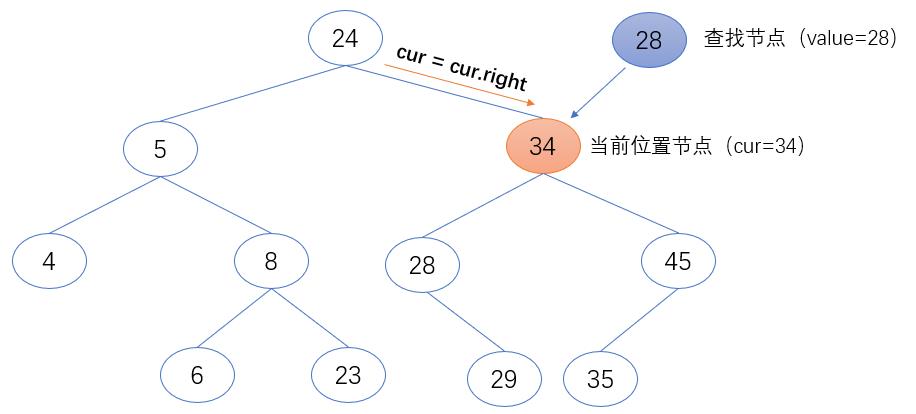
2. 如果当前位置节点（cur）的值小于要查找的值（value），返回当前位置节点（cur）。

 

if cur.value < value:
    cur = cur.right

 

 

 

 

 

 

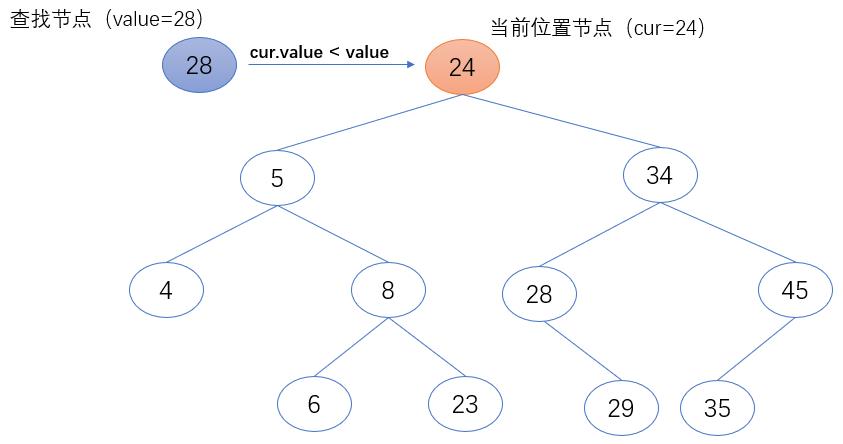
3. 如果当前位置节点（cur）的值小于要查找的值（value），返回当前位置节点（cur）。

 

if cur.value > value:
    cur = cur.left

 

 

 

 

 

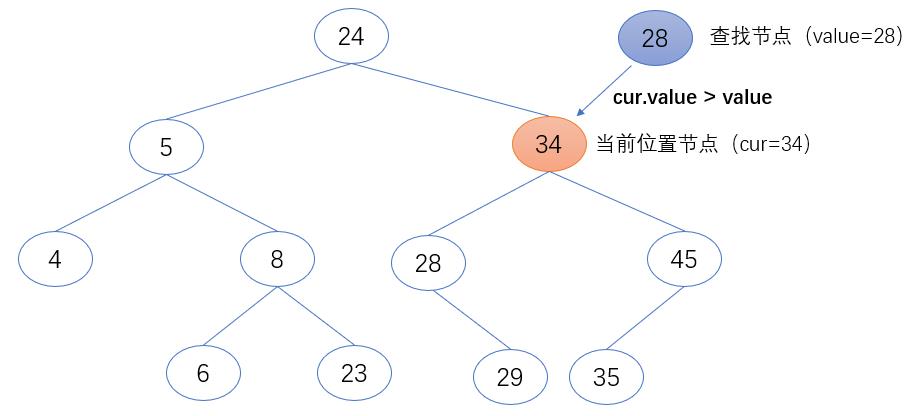
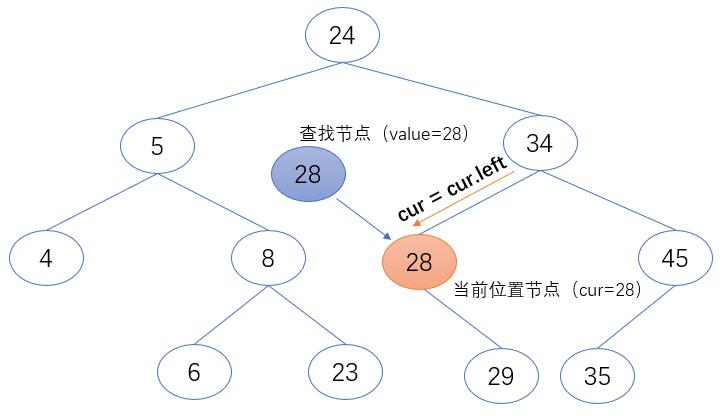
第三步：如果cur的值为None，返回空。即查找的二叉搜索树为空树。

 

return None

 

查找功能代码汇总：

def search(self,value):
    cur = self.root
    while cur != None:
        if cur.value == value:
            return cur
        elif cur.value < value:
            cur = cur.right
        else:
            cur = cur.left
    return None

　　

方法（bfs_delete）：实现删除功能

第一步：将待删除节点（node）的父节点赋值给father变量。

 

def delete(self,node):
    father = node.father

　　

第二步：判断待删除节点（node）的左子树是否为空

 

1. 待删除节点（node）的左子树为空

if node.left == None:

 

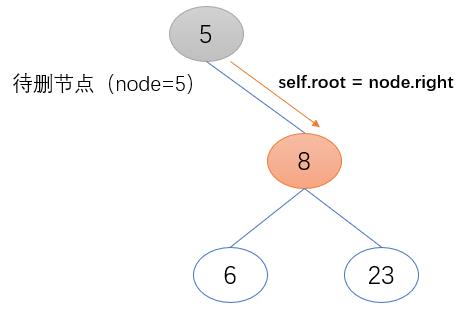
a)     待删除节点（node）为根节点

 

将待删除节点（node）的右子节点置为新的根节点（root），且其如果为非空，将其父节点（node.right.father）赋值为空。

 

if father == None:
    self.root = node.right
    if node.right != None:
        node.right.father = None

 

 

 

 

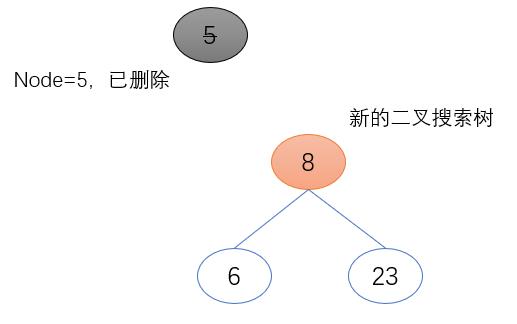
b)     待删除节点（node）为其父节点的左子节点

 

待删除节点（node）的右子节点（node.right）取代其原来的位置，成为其父节点新的左子节点（father.left）。且其右子节点（node.right）不为空，将待删除节点（node）的父节点赋值给它的父节点（node.right.father）

 

if father.left == node:
    father.left = node.right
    if node.right != None:
        node.right.father = father

 

　

 

 

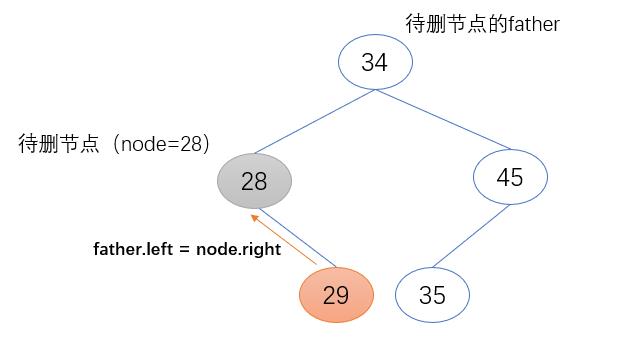
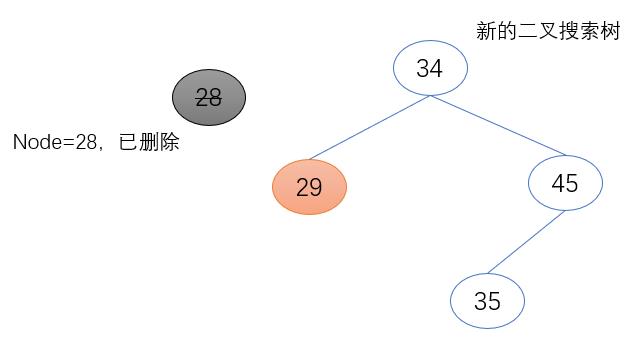
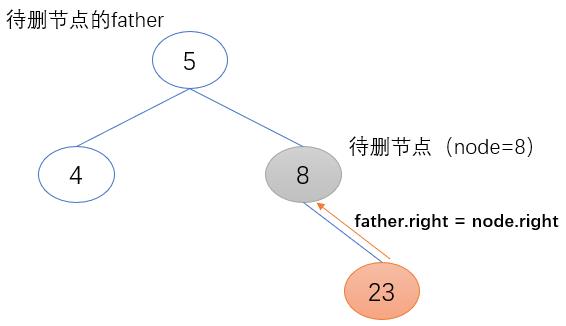
c)     待删除节点（node）为其父节点的右子节点

 

待删除节点（node）的右子节点（node.right）取代其原来的位置，成为其父节点新的右子节点（father.right）。且其右子节点（node.right）不为空，将待删除节点（node）的父节点赋值给它的父节点（node.right.father）

 

if father.right == node:
    father.right = node.right
    if node.right != None:
        node.right.father = father

 

 

 

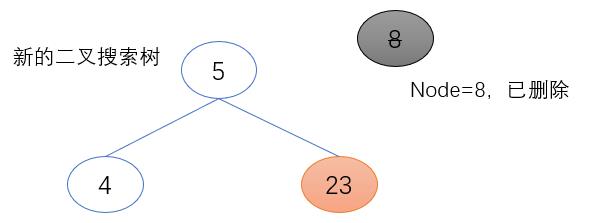
2. 待删除节点（node）的左子树不为空

 

第一步：将待删除节点（node）的右子树挂到其左子树最后一层的右子节点下

 

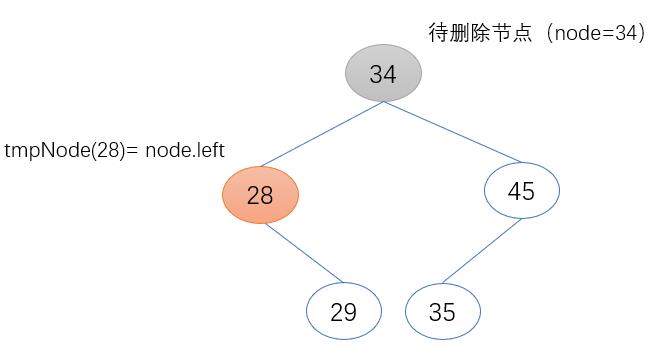
a)     将待删除节点的左子节点（node.left）存到临时变量tmpNode中

 

tmpNode = node.left

 

 

b)     递归找到node.left的最后一层右子节点

 

while tmpNode.right != None:
    tmpNode = tmpNode.right

 

 

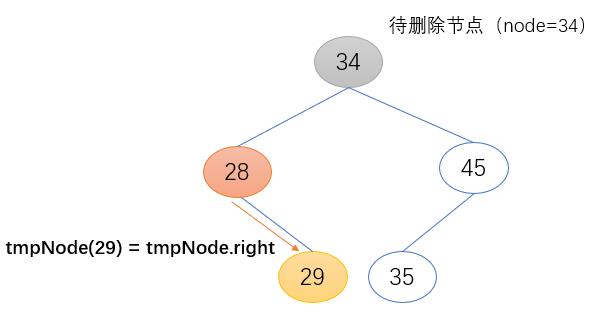
c)     将待删节点的右子树（node.right）挂到node.left的最后一层右子节点下

 

tmpNode.right = node.right

 

d)     将node.right的父节点设置为待删节点左子树中的最后一层的右子节点

 

if node.right != None:
    node.right.father = tmpNode

 

　

 

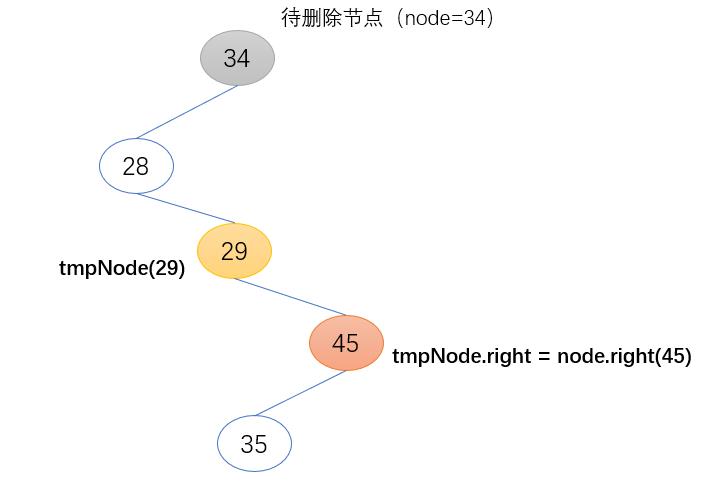
第二步：开始删除node

 

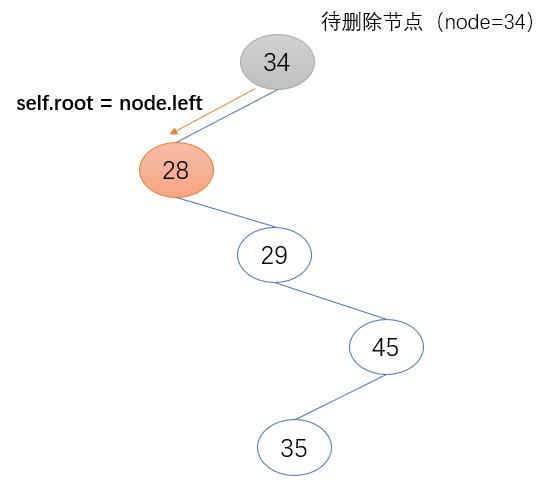
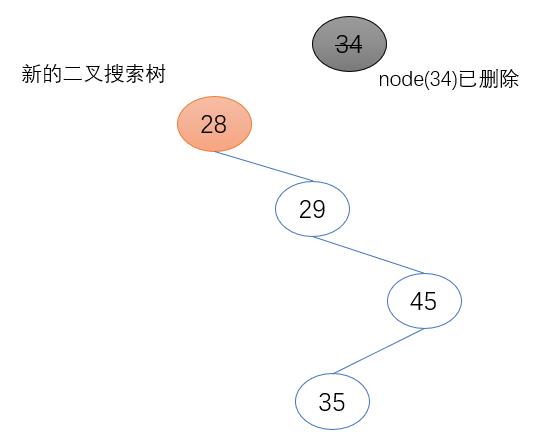
1.待删除节点为根节点

 

将待删除节点的左子节点（node.left）设置为根节点（self.root），并将其父节点设置为空。

 

if father == None:
    self.root = node.left
    node.left.father = None

　　

 

 

 

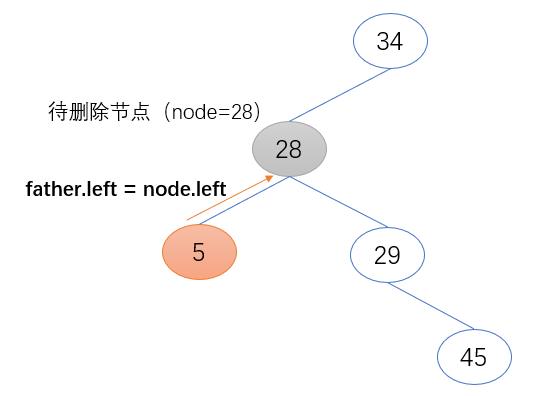
2.待删除节点为根节点的左子节点

 

待删除节点的左子节点（node.left）取代待删节点的位置，并将其父节点设置为待删除节点的父节点。

 

if father.left == node:
    father.left = node.left
    node.left.father = father

 

 

 

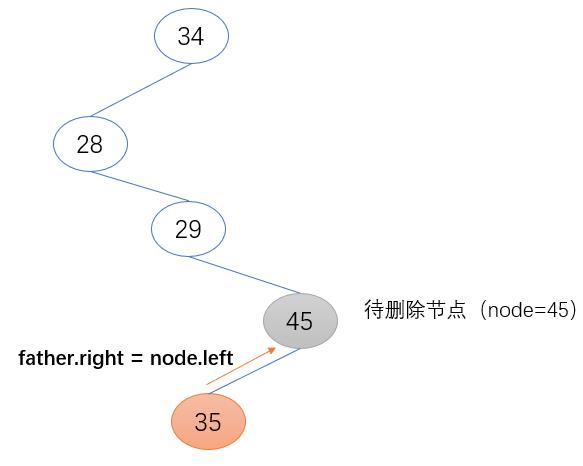
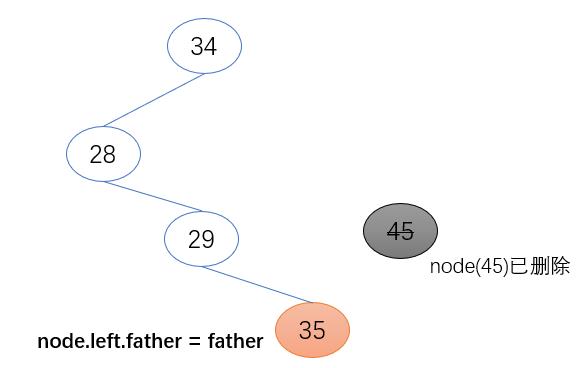
3. 待删除节点为根节点的右子节点

 

待删除节点的左子节点（node.left）取代待删节点的位置，并将其父节点设置为待删除节点的父节点

 

if father.right == node:
    father.right = node.left
    node.left.father = father

 

 

 

删除功能代码汇总：

def delete(self,node):
    father = node.father
    if node.left == None:
        if father == None:
            self.root = node.right
            if node.right != None:
                node.right.father = None
        elif father.left == node:
            father.left = node.right
            if node.right != None:
                node.right.father = father
        else:
            father.right = node.right
            if node.right != None:
                node.right.father = father
        return \'delete successfully\'
    tmpNode = node.left
    while tmpNode.right != None:
        tmpNode = tmpNode.right

    tmpNode.right = node.right
    if node.right != None:
        node.right.father = tmpNode

    if father == None:
        self.root = node.left
        node.left.father = None
    elif father.left == node:
        father.left = node.left
        node.left.father = father
    else:
        father.right = node.left
        node.left.father = father
    node = None
    return \'delete successfully\'

　

综上，二叉搜索树代码

# encoding=utf-8
import queue

class TreeNode(object):
    def __init__(self,val):
        self.value = val
        self.left = None
        self.right = None
        self.father = None

class BST(object):
    def __init__(self,nodeList):
        self.root = None
        for node in nodeList:
            self.bfs_insert(node)

    def bfs_insert(self,node):
        father = None
        cur = self.root

        while cur != None:
            if cur.value == node.value:
                return -1
            father = cur
            if node.value < cur.value:
                cur = cur.left
            else:
                cur = cur.right
        node.father = father
        if father == None:
            self.root = node
        elif node.value < father.value:
            father.left = node
        else:
            father.right = node

    def bfs(self):
        if self.root == None:
            return None
        retList = []
        q = queue.Queue()
        q.put(self.root)
        while q.empty() is not True:
            node = q.get()
            retList.append(node.value)
            if node.left != None:
                q.put(node.left)
            if node.right != None:
                q.put(node.right)
        return retList

    def bfs_search(self,value):
        cur = self.root
        while cur != None:
            if cur.value == value:
                return cur
            elif cur.value < value:
                cur = cur.right
            else:
                cur = cur.left
        return None

    def bfs_delete(self,node):
        father = node.father
        if node.left == None:
            if father == None:
                self.root = node.right
                if node.right != None:
                    node.right.father = None
            elif father.left == node:
                father.left = node.right
                if node.right != None:
                    node.right.father = father
            else:
                father.right = node.right
                if node.right != None:
                    node.right.father = father
            return \'delete successfully\'
        tmpNode = node.left
        while tmpNode.right != None:
            tmpNode = tmpNode.right

        tmpNode.right = node.right
        if node.right != None:
            node.right.father = tmpNode

        if father == None:
            self.root = node.left
            node.left.father = None
        elif father.left == node:
            father.left = node.left
            node.left.father = father
        else:
            father.right = node.left
            node.left.father = father
        node = None
        return \'delete successfully\'

if __name__ == \'__main__\':
    varList = [24,34,5,4,8,23,45,35,28,6,29]
    nodeList = [TreeNode(var) for var in varList]
    bst = BST(nodeList)
    print (bst.bfs())
    node = bst.bfs_search(34)
    bst.bfs_delete(node)
    print (bst.bfs())