基于matlab实现生成模糊fis文件,包括模糊隶属函数和模糊规则等,不使用fuzzy工具箱

Posted 2023-05-15 51matlab

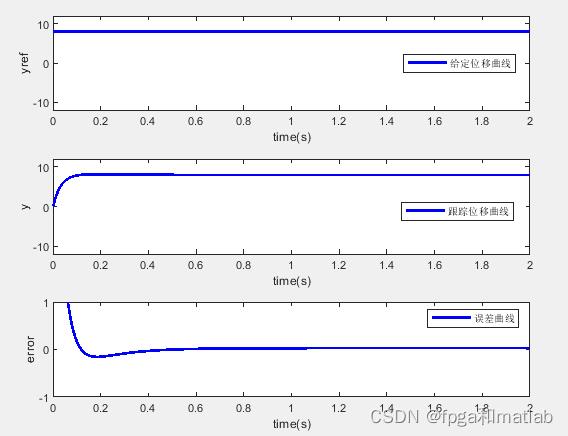
1.算法仿真效果

matlab2022a仿真结果如下：

 

 

 

 

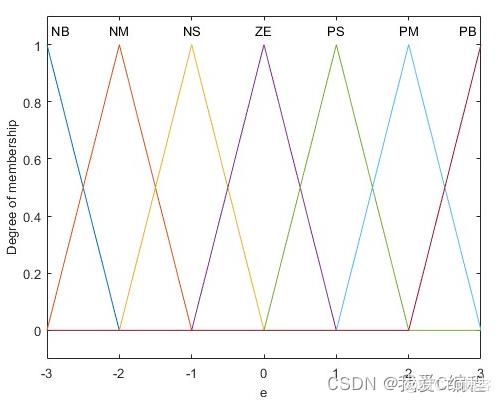
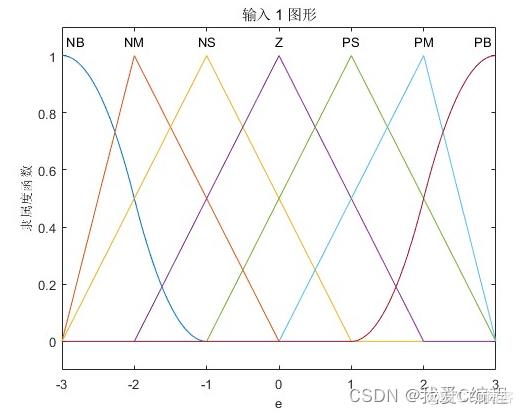
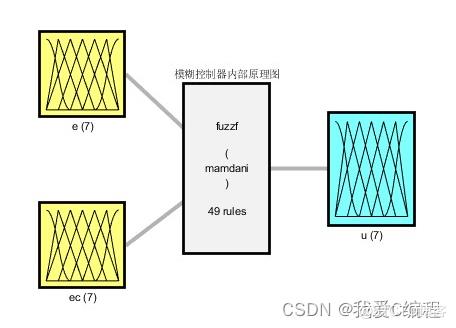
2.算法涉及理论知识概要

       Zadeh创立的模糊数学，对不明确系统的控制有极大的贡献，自七十年代以后，一些实用的模糊控制器的相继出现，使得我们在控制领域中又向前迈进了一大步。模糊逻辑控制(Fuzzy Logic Control)简称模糊控制(Fuzzy Control)，是以模糊集合论、模糊语言变量和模糊逻辑推理为基础的一种计算机数字控制技术。1965年，美国的L.A.Zadeh创立了模糊集合论；1973年他给出了模糊逻辑控制的定义和相关的定理。1974年，英国的E.H.Mamdani首次根据模糊控制语句组成模糊控制器，并将它应用于锅炉和蒸汽机的控制，获得了实验室的成功。这一开拓性的工作标志着模糊控制论的诞生。模糊控制实质上是一种非线性控制，从属于智能控制的范畴。模糊控制的一大特点是既有系统化的理论，又有大量的实际应用背景。模糊控制的发展最初在西方遇到了较大的阻力；然而在东方尤其是日本，得到了迅速而广泛的推广应用。近20多年来，模糊控制不论在理论上还是技术上都有了长足的进步，成为自动控制领域一个非常活跃而又硕果累累的分支。其典型应用涉及生产和生活的许多方面，例如在家用电器设备中有模糊洗衣机、空调、微波炉、吸尘器、照相机和摄录机等；在工业控制领域中有水净化处理、发酵过程、化学反应釜、水泥窑炉等；在专用系统和其它方面有地铁靠站停车、汽车驾驶、电梯、自动扶梯、蒸汽引擎以及机器人的模糊控制。

 

       模糊控制将人的经验知识转化为控制策略，不要求精确的数学模型，只需现场操作人员的经验知识，使模型难以确定的系统得以有效的控制，因此在对象参数发生变化的时候，模糊控制仍能达到较为满意的控制效果。但模糊控制的控制作用较粗糙，无法从根本上消除静态误差，控制精度较低，于是把模糊控制整合到PID控制器中，既保持了PID控制器的结构简单、适用性强和整定方便等优点，又通过智能技术调整了PID控制器的参数，以适应被控对象特性的变化。考虑到控制规则的灵活与细致性兼顾其简单与易行的要求，这里选取七个语言等级作为本文所设计的模糊控制器的语言等级，从负的最大到正的最大依次为：负大(NB)、负中(NM)、负小(NS)、零(ZO)、正小(PS)、正中(PM)、正大(PB)。

 

        常用的隶属函数有矩形分布、梯形分布、三角形分布、柯西分布和正态分布等。隶属函数曲线的形状会导致不同的控制特性，隶属度函数曲线形状较尖的模糊子集器分辨率较高，控制灵敏度也较高；相反，隶属度函数曲线形状较缓，控制特性也较平缓，系统稳定性也较好。因此在选择模糊变量的模糊隶属函数时，在误差较大的区域采用低分辨率的模糊集，在误差较小的区域采用高分辨率的模糊集。

 

       模糊规则是指根据人的直觉思维推理，依据系统输出的误差及误差的变化趋势来消除系统误差的控制规则，它是由专家或者经验人员总结出来的。控制规则的基本形式为

 

 

 

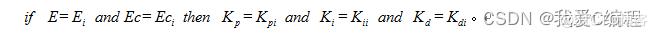
       建立模糊控制规则表的基本原则是：当误差大或较大时，选取控制量以尽快消除误差为主；而当误差较小时，选取控制量要注意防止超调，以系统的稳定性为主要出发点。误差为正时与误差为负时相类同，相应的符号都要变化。

 

 

 

 

3.MATLAB核心程序

 

%模糊规则表
rulea = [7,7,7,7,7,4,4,
         7,7,7,7,6,4,4,
         6,6,6,6,4,3,3,
         6,6,5,4,3,2,2,
         5,5,4,3,2,2,2,
         4,4,2,1,1,1,1,
         4,4,2,1,1,1,1];
%% 定义输入输出变量，并赋值
tip= newfis(\'fuzzy\');      %创建一个模糊推理系统（FIS）
A1=-3;B1=3;                %定义e的取值范围[A1,B1]
C1=(B1-A1)/6;              %6为变量个数-1
A2=-6;B2=6;                %定义ec的取值范围[A2,B2]
C2=(B2-A2)/6;              %6为变量个数-1
A3=-9;B3=9;                %定义u的取值范围[A3,B3]
C3=(B3-A3)/6;              %6为变量个数-1
%% 编写输入输出变量，  均分论域
%设置输入参数e
tip = addvar(tip, \'input\',\'e\',[A1,B1]); 
tip = addmf(tip,\'input\',1,\'NB\',\'trimf\',[A1,A1,A1+C1]);
% tip = addmf(tip,\'input\',1,\'NB\',\'zmf\',[A1,A1+C1]);
tip = addmf(tip,\'input\',1,\'NM\',\'trimf\',[A1,A1+C1,A1+2*C1]);
tip = addmf(tip,\'input\',1,\'NS\',\'trimf\',[A1+C1,A1+2*C1,A1+3*C1]);
tip = addmf(tip,\'input\',1,\'ZE\',\'trimf\',[A1+2*C1,A1+3*C1,A1+4*C1]);
tip = addmf(tip,\'input\',1,\'PS\',\'trimf\',[A1+3*C1,A1+4*C1,A1+5*C1]);
tip = addmf(tip,\'input\',1,\'PM\',\'trimf\',[A1+4*C1,A1+5*C1,B1]);
% tip = addmf(tip,\'input\',1,\'PB\',\'smf\',[A1+5*C1,B1]);
tip = addmf(tip,\'input\',1,\'PB\',\'trimf\',[A1+5*C1,B1,B1]);
................................................................
%% 模糊规则
rulelist = [ 1,1,rulea(1),1,1;          %模糊规则，共49条
             1,2,rulea(2),1,1;
             1,3,rulea(3),1,1;
             1,4,rulea(4),1,1;
             1,5,rulea(5),1,1;
             1,6,rulea(6),1,1;
             1,7,rulea(7),1,1;
             
             2,1,rulea(8),1,1;
             2,2,rulea(9),1,1;
             2,3,rulea(10),1,1;
             2,4,rulea(11),1,1;
             2,5,rulea(12),1,1;
             2,6,rulea(13),1,1;
             2,7,rulea(14),1,1;
             
             3,1,rulea(15),1,1;
             3,2,rulea(16),1,1;
             3,3,rulea(17),1,1;
             3,4,rulea(18),1,1;
             3,5,rulea(19),1,1;
             3,6,rulea(20),1,1;
             3,7,rulea(21),1,1;
.................................................................
             
             6,1,rulea(36),1,1;
             6,2,rulea(37),1,1;
             6,3,rulea(38),1,1;
             6,4,rulea(39),1,1;
             6,5,rulea(40),1,1;
             6,6,rulea(41),1,1;
             6,7,rulea(42),1,1;
             
             7,1,rulea(43),1,1;
             7,2,rulea(44),1,1;
             7,3,rulea(45),1,1;
             7,4,rulea(46),1,1;
             7,5,rulea(47),1,1;
             7,6,rulea(48),1,1;
             7,7,rulea(49),1,1;    

 

　　

 

MATLAB教程案例71通过MATLAB编程实现模糊控制器2——编程实现模糊控制(不使用FIS Editor)

欢迎订阅《FPGA学习入门100例教程》、《MATLAB学习入门100例教程》

本课程学习成果预览(低超调,快速收敛)

目录

1.软件版本

2.模糊控制器的MATLAB编程实现