四 图卷积的公式推导
Posted kuafuzhuiri
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了四 图卷积的公式推导相关的知识,希望对你有一定的参考价值。
1 定义图上的卷积操作
假定有一个函数,输入是图的邻接矩阵,输出是L/Lsym这种性质比较好的矩阵
F(A)可以分解:

那么我们定义图上的卷积操作
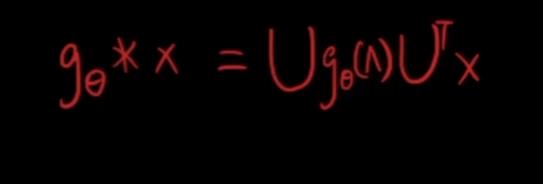
先让X去新的域,再进行操作,最后用逆变换变回来
作出限制:gΘ(尖)是λ的多项式函数:
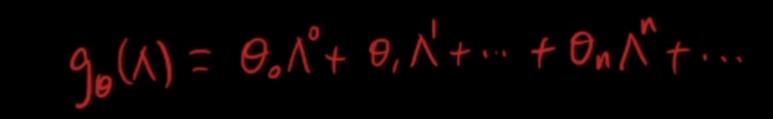
2 限制的好处
如果上述函数是多项式函数,那么就需要做特征分解了


3 实际中使用了切比雪夫多项式,使用上述多项式会有梯度消失和爆炸的问题

切比雪夫多项式的优点:
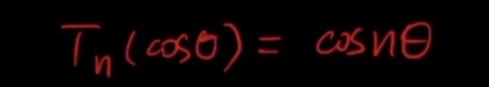
不管n多大,数值摆动的趋势是稳定的
自变量必须在[-1,1]之间,就是矩阵的特征值再[-1.,1]
上述Lsym的特征值的范围是[1,2],只要Lsym - E即可满足条件
F(A) = Lsym - E
卷积的定位写作:
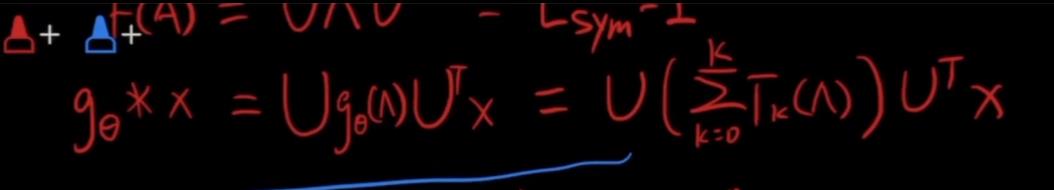
化解为:
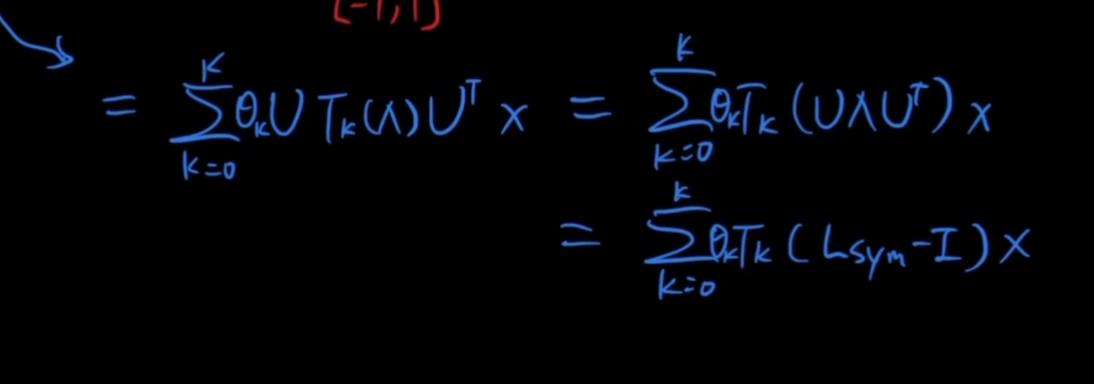
θ:为学习的系数
以上公式的复杂度依然很高,需要计算K次方,GCN做了一个近似操作,K只要0和1
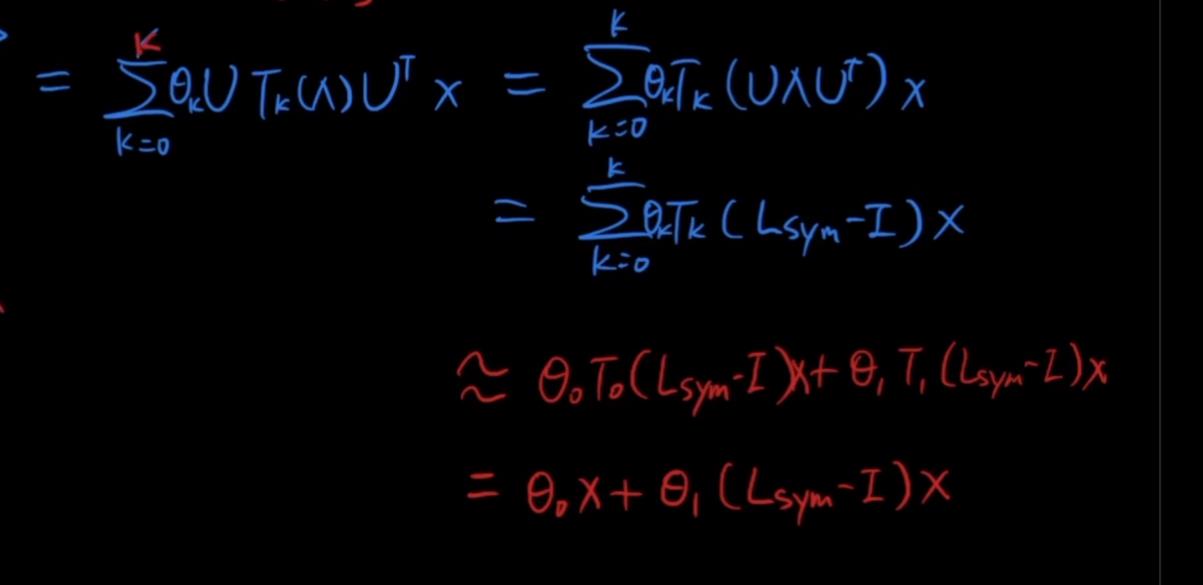
Lsym的本质是:
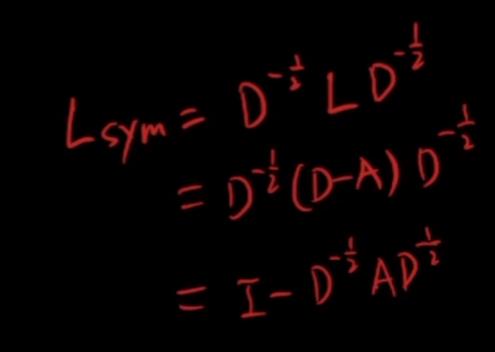
将上述公式得到的Lsym-I的结果带入展开:

GCN在推导中使用了很多正则化和trick
(1)θ0和θ1共享参数
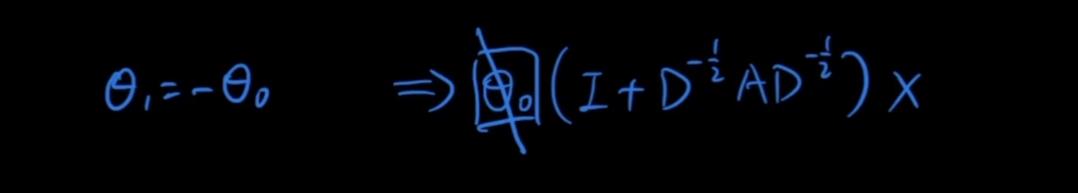
(2)把I直接加到A中
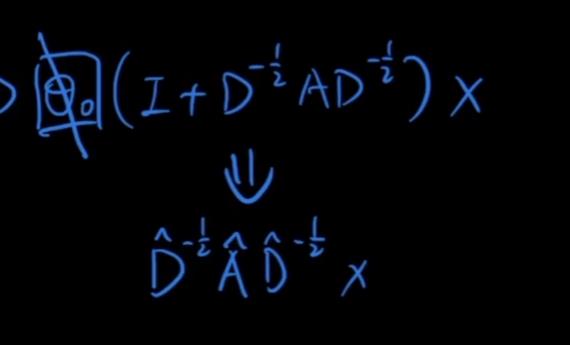
使用原因是加入trick后效果很好:
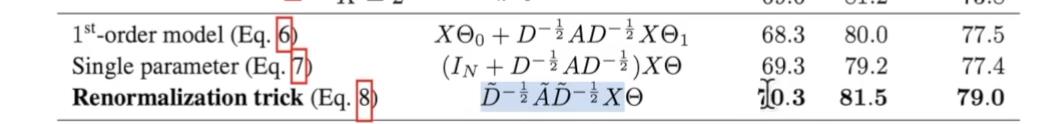
后续的工作是一阶近似扩展到更高阶的近似方式
7.2 图卷积算子,图卷积的演变过程 意境级讲解
第一代图卷积
论文1中谱图卷积的思想是:既然无法直接在空域对图进行卷积,那么将图信号映射到频域后再做卷积操作。
1、需要Graph上的傅里叶变换和卷积定理等知识:
5.5 卷积、卷积定理和傅里叶变换的关系及其性质_炫云云-CSDN博客
2、图卷积
在上面的基础上,利用卷积定理类比来将卷积运算,推广到Graph上。
卷积定理:函数卷积的傅里叶变换是函数傅立叶变换的点积,即对于函数
f
(
t
)
f(t)
f(t) 与
g
(
t
)
g(t)
g(t)两者的卷积是其函数傅立叶变换点积的逆变换:
f
∗
g
=
F
−
1
[
f
^
(
ω
)
g
^
(
ω
)
]
=
1
2
Π
∫
f
^
(
ω
)
g
^
(
ω
)
e
i
ω
t
d
ω
(1)
f*g=\\mathscr{F}^{-1}\\left[ \\hat{f}(\\omega)\\hat{g}(\\omega) \\right]=\\frac{1}{2\\Pi}\\int_{}^{} \\hat{f}(\\omega)\\hat{g}(\\omega)e^{i\\omega t} d\\omega \\tag1
f∗g=F−1[f^(ω)g^(ω)]=2Π1∫f^(ω)g^(ω)eiωtdω(1)
根据公式 (1)与文章图上的傅里叶变换和逆变换中图上的傅里叶变换公式,图信号
x
x
x 与卷积核
g
g
g 在图上的卷积可按下列步骤求出:
(
g
∗
x
)
G
=
F
−
1
[
F
g
⋅
F
x
]
=
F
−
1
[
U
T
g
⋅
U
T
x
]
=
F
−
1
[
g
^
⋅
U
T
x
]
(2)
\\begin{aligned} ( g*x)_{G} &=\\mathscr{F}^{-1}[ \\mathscr{F}{g} \\cdot \\mathscr{F}{x} ] \\\\ &=\\mathscr{F}^{-1} \\left[ \\mathbf{U}^{T} g \\cdot \\mathbf{U}^{T} x\\right] \\\\&= \\mathscr{F}^{-1} \\left[ \\hat g \\cdot \\mathbf{U}^{T} x\\right] \\end{aligned} \\tag 2
(g∗x)G=F−1[Fg⋅Fx]=F−1[UTg⋅UTx]=F−1[g^⋅UTx](2)
上式表示时域信号
x
x
x 和
g
g
g (卷积核等等
)
)
) 的卷积等价于将信号转换到频谱域做点乘后再逆变换回来。其中, 向量
x
x
x 与向量
g
^
\\hat{g}
g^ 的元素点积,等价于将
g
^
\\hat{g}
g^ 组织成对角矩阵的 形式进行矩阵乘法, 可得:
卷积核 g g g 的傅里叶变换写成对角矩阵的形式即为: ( g ^ ( λ 1 ) ⋱ g ^ ( λ N ) ) \\left(\\begin{matrix}\\hat g(\\lambda_1) & \\\\&\\ddots \\\\ &&\\hat g(\\lambda_N) \\end{matrix}\\right) ⎝⎛g^(λ1)⋱g^(λN)⎠⎞
g ^ ( λ l ) = ∑ i = 1 N g ( i ) u l ∗ ( i ) \\hat{g}(\\lambda_l)=\\sum_{i=1}^{N}{g(i) u_l^*(i)} g^(λl)=∑i=1Ng(i)ul∗(i) 是根据需要设计的卷积核 g g g在Graph上的傅里叶变换。
两者的傅立叶变换乘积即为:
(
g
^
(
λ
1
)
⋱
g
^
(
λ
N
)
)
U
T
x
\\left(\\begin{matrix}\\hat g(\\lambda_1) & \\\\&\\ddots \\\\ &&\\hat g(\\lambda_N) \\end{matrix}\\right)U^Tx
⎝⎛g^(λ1)⋱g^(λN)⎠⎞UTx,即 以上是关于四 图卷积的公式推导的主要内容,如果未能解决你的问题,请参考以下文章
(
g
∗
x
)
=
F
−
1
[
g
^
⋅
U
T
x
]
=
F
−
1
[
diag
[
g
^
1
,
…
,
g
^
N
]
U
T
x
]
(3)
\\begin{aligned} ( g*x) &=\\mathcal{F}^{-1}\\left[\\hat g \\cdot \\mathbf{U}^{T} x\\right] \\\\ &=\\mathcal{F}^{-1}\\left[\\operatorname{diag} \\left[\\hat{g}_{1}, \\ldots, \\hat{g}_{N}\\right] \\mathbf{U}^{T} x\\right] \\end{aligned} \\tag 3
(g∗x)=F−1[g^⋅UTx]=F−1[diag[g^1,…,g^N]UTx](3)
根据图上的逆变换计算公式,再乘以
U
U
U 求两者傅立叶变换乘积的逆变换,则求出卷积:
(
g
∗
x
)
=
U
(
g
^