LeetCode 双周赛 104(2023/05/13)流水的动态规划,铁打的结构化思考
Posted pengxurui
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了LeetCode 双周赛 104(2023/05/13)流水的动态规划,铁打的结构化思考相关的知识,希望对你有一定的参考价值。
本文已收录到 AndroidFamily,技术和职场问题,请关注公众号 [彭旭锐] 提问。
T1. 老人的数目(Easy)
- 标签:模拟、计数
T2. 矩阵中的和(Medium)
- 标签:模拟、排序
T3. 最大或值(Medium)
- 标签:动态规划、前后缀分解、贪心

T4. 英雄的力量(Hard)
- 标签:排序、贪心、动态规划、数学
T1. 老人的数目(Easy)
https://leetcode.cn/problems/number-of-senior-citizens/
简单模拟题,直接截取年龄字符后计数即可:
class Solution
fun countSeniors(details: Array<String>): Int
return details.count it.substring(11, 13).toInt() > 60
除了将字符串转为整数再比较外,还可以直接比较子串与 “60” 的字典序:
class Solution
fun countSeniors(details: Array<String>): Int
return details.count it.substring(11, 13) > "60"
复杂度分析:
- 时间复杂度:$O(n)$ 其中 n 为 details 数组的长度;
- 空间复杂度:$O(1)$ 仅使用常量级别空间。
T2. 矩阵中的和(Medium)
https://leetcode.cn/problems/sum-in-a-matrix/
简单模拟题。
先对每一行排序,再取每一列的最大值。
class Solution
fun matrixSum(nums: Array<IntArray>): Int
var ret = 0
for (row in nums)
row.sort()
for (j in 0 until nums[0].size)
var mx = 0
for (i in 0 until nums.size)
mx = Math.max(mx, nums[i][j])
ret += mx
return ret
复杂度分析:
- 时间复杂度:$O(nmlgm + nm)$ 其中 n 和 m 分别为矩阵的行数和列数,排序时间 $O(nmlgm)$,扫描时间 $O(nm)$;
- 空间复杂度:$O(lgm)$ 排序递归栈空间。
T3. 最大或值(Medium)
https://leetcode.cn/problems/maximum-or/
题目描述
给你一个下标从 0 开始长度为 n 的整数数组 nums 和一个整数 k 。每一次操作中,你可以选择一个数并将它乘 2 。
你最多可以进行 k 次操作,请你返回 **nums[0] | nums[1] | ... | nums[n - 1] 的最大值。
a | b 表示两个整数 a 和 b 的 按位或 运算。
示例 1:
输入:nums = [12,9], k = 1
输出:30
解释:如果我们对下标为 1 的元素进行操作,新的数组为 [12,18] 。此时得到最优答案为 12 和 18 的按位或运算的结果,也就是 30 。
示例 2:
输入:nums = [8,1,2], k = 2
输出:35
解释:如果我们对下标 0 处的元素进行操作,得到新数组 [32,1,2] 。此时得到最优答案为 32|1|2 = 35 。
提示:
1 <= nums.length <= 1051 <= nums[i] <= 1091 <= k <= 15
问题结构化

1、概括问题目标
计算可以获得的最大或值。
2、分析问题要件
在每次操作中,可以从数组中选择一个数乘以 2,亦相当于向左位移 1 位。
3、观察问题数据
- 数据量:问题数据量上界为 $10^5$,要求算法时间复杂度低于 $O(n^2)$;
- 数据大小:元素值的上界为 $10^9$,操作次数 k 的上界为 15(这个性质有什么用呢?);
- 输出结果:以长整型 Long 的形式返回结果。
4、观察测试用例
以示例 1 nums=[12, 9], k = 1 为例,最优答案是对 9 乘以 2,说明操作最大值并不一定能获得最大或值。
5、提高抽象程度
- 权重:二进制位越高的位对数字大小的影响越大,因此我们应该尽量让高位的二进制位置为 1;
- 是否为决策问题?由于每次操作有多种位置选择,因此这是一个决策问题。
6、具体化解决手段
- 1、贪心:结合「数据大小」分析,由于操作次数 k 的上界为 15 次,无论如何位移都不会溢出 Long。因此,我们可以将 k 次位移操作作用在同一个数字上,尽可能让高位的位置置为 1;
- 2、动态规划(背包):假设已经计算出数组前 i - 1 个元素能够组成的最大或值,那么考虑拼接 nums[i],可以选择不操作 nums[i],也可以选择在 nums[i] 上操作 x 次,那么问题就变成「前 i - 1 个元素中操作 k - x 次的最大或值」与「num[i] 操作 x 次的或值」合并的或值。「前 i - 1 个元素中操作 k - x 次的最大或值」这是一个与原问题相似但规模更小的子问题,可以用动态规划解决,更具体地可以用背包问题模型解决。
题解一(贪心 + 前后缀分解)
枚举所有数字并向左位移 k 次,计算所有方案的最优解:
class Solution
fun maximumOr(nums: IntArray, k: Int): Long
val n = nums.size
// 前后缀分解
val pre = IntArray(n + 1)
val suf = IntArray(n + 1)
for (i in 1 .. n)
pre[i] = pre[i - 1] or nums[i - 1]
for (i in n - 1 downTo 0)
suf[i] = suf[i + 1] or nums[i]
var ret = 0L
for (i in nums.indices)
ret = Math.max(ret, (1L * nums[i] shl k) or pre[i].toLong() or suf[i + 1].toLong())
return ret
由于每个方案都需要枚举前后 n - 1 个数字的或值,因此这是一个 $O(n^2)$ 的解法,会超出时间限制。我们可以采用空间换时间的策略,预先计算出每个位置(不包含)的前后缀的或值,这个技巧就是「前后缀分解」。
在实现细节上,我们可以把其中一个前缀放在扫描的时候处理。
class Solution
fun maximumOr(nums: IntArray, k: Int): Long
val n = nums.size
// 前后缀分解
val suf = IntArray(n + 1)
for (i in n - 1 downTo 0)
suf[i] = suf[i + 1] or nums[i]
var ret = 0L
var pre = 0L
for (i in nums.indices)
ret = Math.max(ret, pre or (1L * nums[i] shl k) or suf[i + 1].toLong())
pre = pre or nums[i].toLong()
return ret
复杂度分析:
- 时间复杂度:$O(n)$ 其中 n 为 nums 数组的长度;
- 空间复杂度:$O(n)$ 后缀或值数组长度空间。
题解二(动态规划)
使用背包问题模型时,定义 dp[i][j] 表示在前 i 个元素上操作 k 次可以获得的最大或值,则有:
- 状态转移方程:$dp[i][j] = maxdp[i-1][j], dp[i - 1][j - x] | (nums[i] << x)$
- 终止条件:$dp[n][k]$
class Solution
fun maximumOr(nums: IntArray, k: Int): Long
val n = nums.size
// 以 i 为止,且移动 k 次的最大或值
val dp = Array(n + 1) LongArray(k + 1)
for (i in 1 .. n)
for (j in 0 .. k)
for (m in 0 .. j)
dp[i][j] = Math.max(dp[i][j], dp[i - 1][j - m] or (1L * nums[i - 1] shl m) /* 移动 m 次 */)
return dp[n][k]
另外,这个背包问题可以取消物品维度来优化空间:
class Solution
fun maximumOr(nums: IntArray, k: Int): Long
val n = nums.size
// 以 i 为止,且移动 k 次的最大或值
val dp = LongArray(k + 1)
for (i in 1 .. n)
// 逆序
for (j in k downTo 0)
for (m in 0 .. j)
dp[j] = Math.max(dp[j], dp[j - m] or (1L * nums[i - 1] shl m) /* 移动 m 次 */)
return dp[k]
- 时间复杂度:$O(n·k^2)$ 其中 n 为 nums 数组的长度;
- 空间复杂度:$O(k)$ DP 数组空间
相似题目:
T4. 英雄的力量(Hard)
https://leetcode.cn/problems/power-of-heroes/
题目描述
给你一个下标从 0 开始的整数数组 nums ,它表示英雄的能力值。如果我们选出一部分英雄,这组英雄的 力量 定义为:
i0,i1,...ik表示这组英雄在数组中的下标。那么这组英雄的力量为max(nums[i0],nums[i1] ... nums[ik])2 * min(nums[i0],nums[i1] ... nums[ik])。
请你返回所有可能的 非空 英雄组的 力量 之和。由于答案可能非常大,请你将结果对 109 + 7 取余。
示例 1:
输入:nums = [2,1,4]
输出:141
解释:
第 1 组:[2] 的力量为 22 * 2 = 8 。
第 2 组:[1] 的力量为 12 * 1 = 1 。
第 3 组:[4] 的力量为 42 * 4 = 64 。
第 4 组:[2,1] 的力量为 22 * 1 = 4 。
第 5 组:[2,4] 的力量为 42 * 2 = 32 。
第 6 组:[1,4] 的力量为 42 * 1 = 16 。
第 7 组:[2,1,4] 的力量为 42 * 1 = 16 。
所有英雄组的力量之和为 8 + 1 + 64 + 4 + 32 + 16 + 16 = 141 。
示例 2:
输入:nums = [1,1,1]
输出:7
解释:总共有 7 个英雄组,每一组的力量都是 1 。所以所有英雄组的力量之和为 7 。
提示:
1 <= nums.length <= 1051 <= nums[i] <= 109
问题结构化
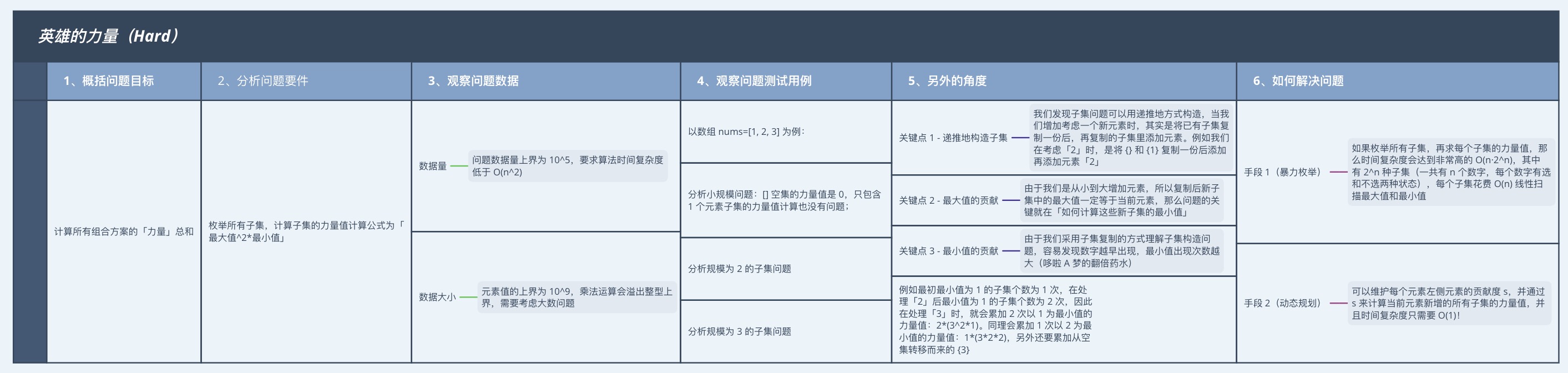
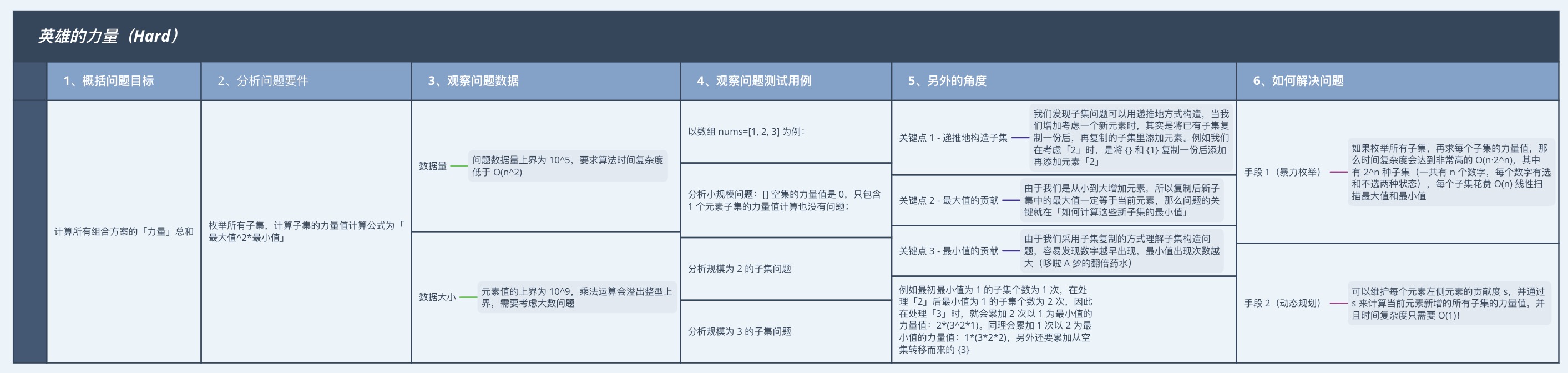
1、概括问题目标
计算所有组合方案的「力量」总和。
2、分析问题要件
枚举所有子集,计算子集的力量值计算公式为$「最大值^2*最小值」$。
3、观察问题数据
- 数据量:问题数据量上界为 $10^5$,要求算法时间复杂度低于 $O(n^2)$;
- 数据大小:元素值的上界为 $10^9$,乘法运算会溢出整型上界,需要考虑大数问题。
4、观察问题测试用例:
以数组 nums=[1, 2, 3] 为例:
- 分析小规模问题:[] 空集的力量值是 0,只包含 1 个元素子集的力量值计算也没有问题;
| 子集 | 最大值 | 最小值 | 力量值 |
|---|---|---|---|
| 0 | 0 | 0 | |
| 1 | 1 | $1^2*1$ | |
| 2 | 2 | $2^2*2$ | |
| 3 | 3 | $3^2*3$ |
- 分析规模为 2 的子集问题:
| 子集 | 最大值 | 最小值 | 力量值 |
|---|---|---|---|
| 2 | 1 | $2^2*1$ | |
| 3 | 1 | $3^2*1$ | |
| 3 | 2 | $3^2*2$ |
- 分析规模为 3 的子集问题:
| 子集 | 最大值 | 最小值 | 力量值 |
|---|---|---|---|
| 3 | 1 | $3^2*1$ |
5、如何解决问题
- 手段 1(暴力枚举):如果枚举所有子集,再求每个子集的力量值,那么时间复杂度会达到非常高的 $O(n·2^n)$,其中有 $2^n$ 种子集(一共有 n 个数字,每个数字有选和不选两种状态),每个子集花费 $O(n)$ 线性扫描最大值和最小值。
至此,问题陷入瓶颈,解决方法是重复以上步骤,枚举掌握的数据结构、算法和技巧寻找思路,突破口在于从另一个角度来理解问题规模(动态规划的思路)。
6、继续观察问题测试用例
同样以数组 nums = [1, 2, 3] 为例:
- 考虑空集的力量值问题:
| 子集 | 最大值 | 最小值 |
|---|---|---|
| 0 | 0 |
- 考虑到「1」为止的力量值问题:
| 子集 | 最大值 | 最小值 |
|---|---|---|
| 0 | 0 | |
| 1 | 1 |
- 考虑到「2」为止的力量值问题:
| 子集 | 最大值 | 最小值 |
|---|---|---|
| 0 | 0 | |
| 1 | 1 | |
| 2 | 2 | |
| 2 | 1 |
- 考虑到「3」为止的力量值问题:
| 子集 | 最大值 | 最小值 |
|---|---|---|
| 0 | 0 | |
| 1 | 1 | |
| 2 | 2 | |
| 2 | 1 | |
| 3 | 3 | |
| 3 | 1 | |
| 3 | 2 | |
| 3 | 1 |
这又说明了什么呢?
- 关键点 1 - 递推地构造子集:
我们发现子集问题可以用递推地方式构造,当我们增加考虑一个新元素时,其实是将已有子集复制一份后,再复制的子集里添加元素。例如我们在考虑「2」时,是将 和 1 复制一份后添加再添加元素「2」。
- 关键点 2 - 最大值的贡献:
由于我们是从小到大增加元素,所以复制后新子集中的最大值一定等于当前元素,那么问题的关键就在「如何计算这些新子集的最小值」。
- 关键点 3 - 最小值的贡献:
由于我们采用子集复制的方式理解子集构造问题,容易发现数字越早出现,最小值出现次数越大(哆啦 A 梦的翻倍药水)。
例如最初最小值为 1 的子集个数为 1 次,在处理「2」后最小值为 1 的子集个数为 2 次,因此在处理「3」时,就会累加 2 次以 1 为最小值的力量值:$2(3^21)$。同理会累加 1 次以 2 为最小值的力量值:$1(32*2)$,另外还要累加从空集转移而来的 3。
至此,问题的解决办法逐渐清晰。
7、解决问题的新手段
- 手段 2(动态规划):
考虑有 a, b, c, d, e 五个数,按顺序从小到大排列,且从小到大枚举。
当枚举到 d 时,复制增加的新子集包括:
- 以 a 为最小值的子集有 4 个:累加力量值 $4(d^2a)$
- 以 b 为最小值的子集有 2 个:累加力量值 $2(d^2b)$
- 以 c 为最小值的子集有 1 个:累加力量值 $1(d^2c)$
另外还有以 d 本身为最小值的子集 1 个:累加力量值 $1(d^2d)$,将 d 左侧元素对结果的贡献即为 s,则有 $pow(d) = d^2*(s + d)$。
继续枚举到 e 是,复制增加的新子集包括:
- 以 a 为最小值的子集有 8 个:累加力量值 $8(e^2a)$
- 以 b 为最小值的子集有 4 个:累加力量值 $4(e^2b)$
- 以 c 为最小值的子集有 2 个:累加力量值 $2(e^2c)$
- 以 d 为最小值的子集有 1个:累加力量值 $1(e^2d)$
另外还有以 e 本身为最小值的子集 1 个:累加力量值 $1(e^2e)$,将 e 左侧元素对结果的贡献即为 s`,则有 $pow(e) = e^2*(s` + e)$。
观察 s 和 s` 的关系:
$s = 4a + 2b + 1*c$
$s = 8a + 4b + 2c + d = s2 + d$
这说明,我们可以维护每个元素左侧元素的贡献度 s,并通过 s 来计算当前元素新增的所有子集的力量值,并且时间复杂度只需要 O(1)!
[4,3,2,1]
1 1 2 4
追加 5:
[5,4,3,2,1]
1 1 2 4 8
题解(动态规划)
根据问题分析得出的递归公式,使用递推模拟即可,先不考虑大数问题:
class Solution
fun sumOfPower(nums: IntArray): Int
var ret = 0L
// 排序
nums.sort()
// 影响因子
var s = 0L
for (x in nums)
ret += (x * x) * (s + x)
s = s * 2 + x
return ret.toInt()
再考虑大数问题:
class Solution
fun sumOfPower(nums: IntArray): Int
val MOD = 1000000007
var ret = 0L
// 排序
nums.sort()
// 影响因子
var s = 0L
for (x in nums)
ret = (ret + (1L * x * x % MOD) * (s + x)) % MOD // x*x 也可能溢出
s = (s * 2 + x) % MOD
return ret.toInt()
实战中我用的是先计算最大影响因子,再累减的写法:
class Solution
fun sumOfPower(nums: IntArray): Int
val MOD = 1000000007
var ret = 0L
val n = nums.size
// 排序
nums.sortDescending()
// 影响因子
var s = 0L
var p = 1L
for (i in 1 until n)
s = (s + nums[i] * p) % MOD
p = (2 * p) % MOD
// 枚举子集
for (i in 0 until n)
val x = nums[i]
ret = (ret + x * x % MOD * (s + x)) % MOD
if (i < n - 1)
s = (s - nums[i + 1]) % MOD
if (s and 1L != 0L)
s += MOD // 奇数除 2 会丢失精度
s = (s / 2) % MOD
return ret.toInt()
复杂度分析:
- 时间复杂度:$O(nlgn)$ 其中 n 为 nums 数组的长度,瓶颈在排序上,计算力量值部分时间复杂度为 O(n);
- 空间复杂度:$O(lgn)$ 排序递归栈空间。
往期回顾
LeetCode第82场双周赛
第82场双周赛
黑暗后是黎明!
6116. 计算布尔二叉树的值
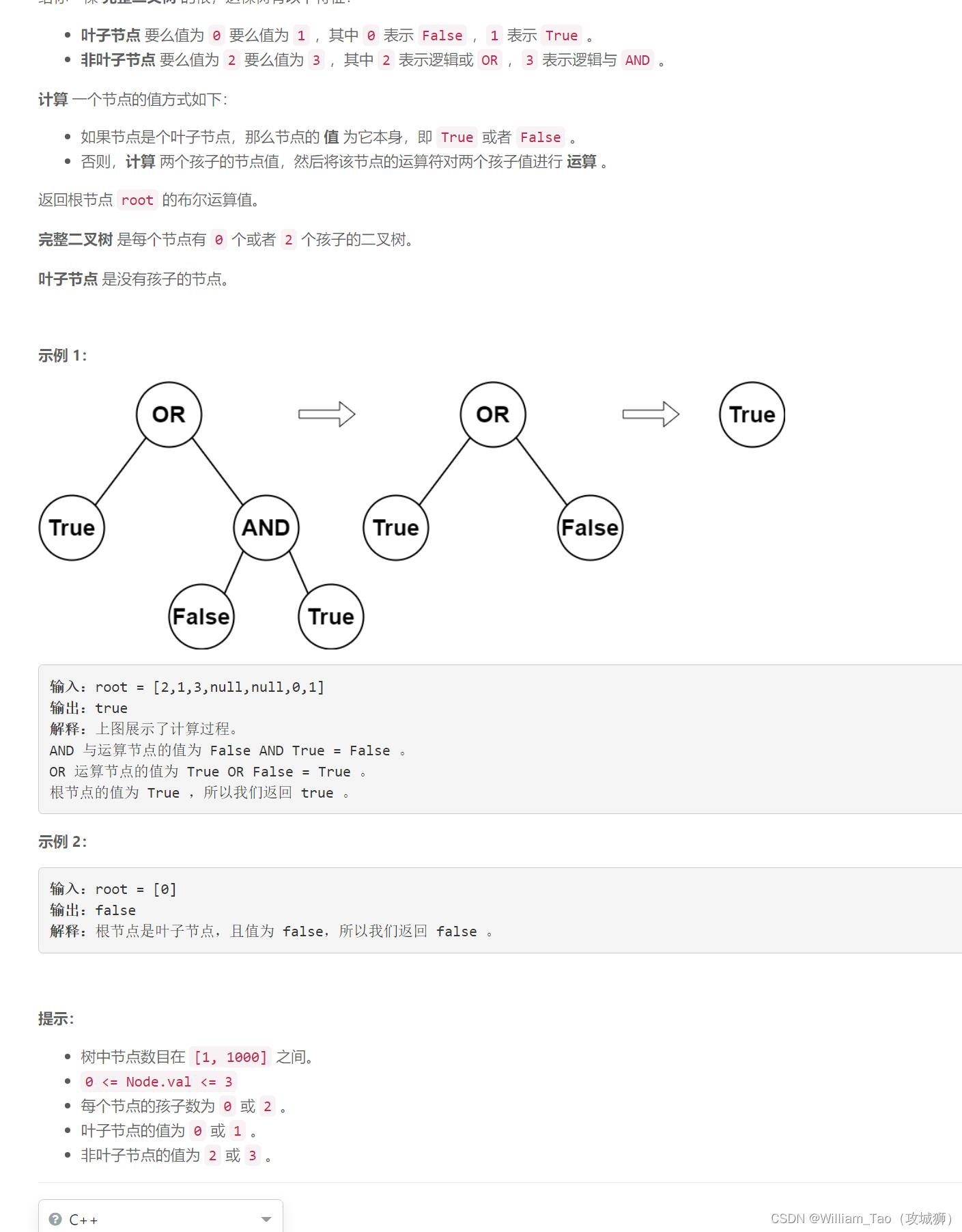
思路:
递归,就是对二叉树的递归遍历,判断非叶子节点是2还是3来进行与/并叶子的计算。
/**
* Definition for a binary tree node.
* struct TreeNode
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr)
* TreeNode(int x) : val(x), left(nullptr), right(nullptr)
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right)
* ;
*/
class Solution
public:
bool evaluateTree(TreeNode* root)
//题目明确说了树中节点数目在 [1, 1000] 之间。所以不可能为空
//完整二叉树,无左孩子一定无有孩子,考虑一边就行
if(!root->left)return root->val;
auto l =evaluateTree(root->left);
auto r=evaluateTree(root->right);
if(root->val==2) return l||r;
return l&&r;
;
6117. 坐上公交的最晚时间
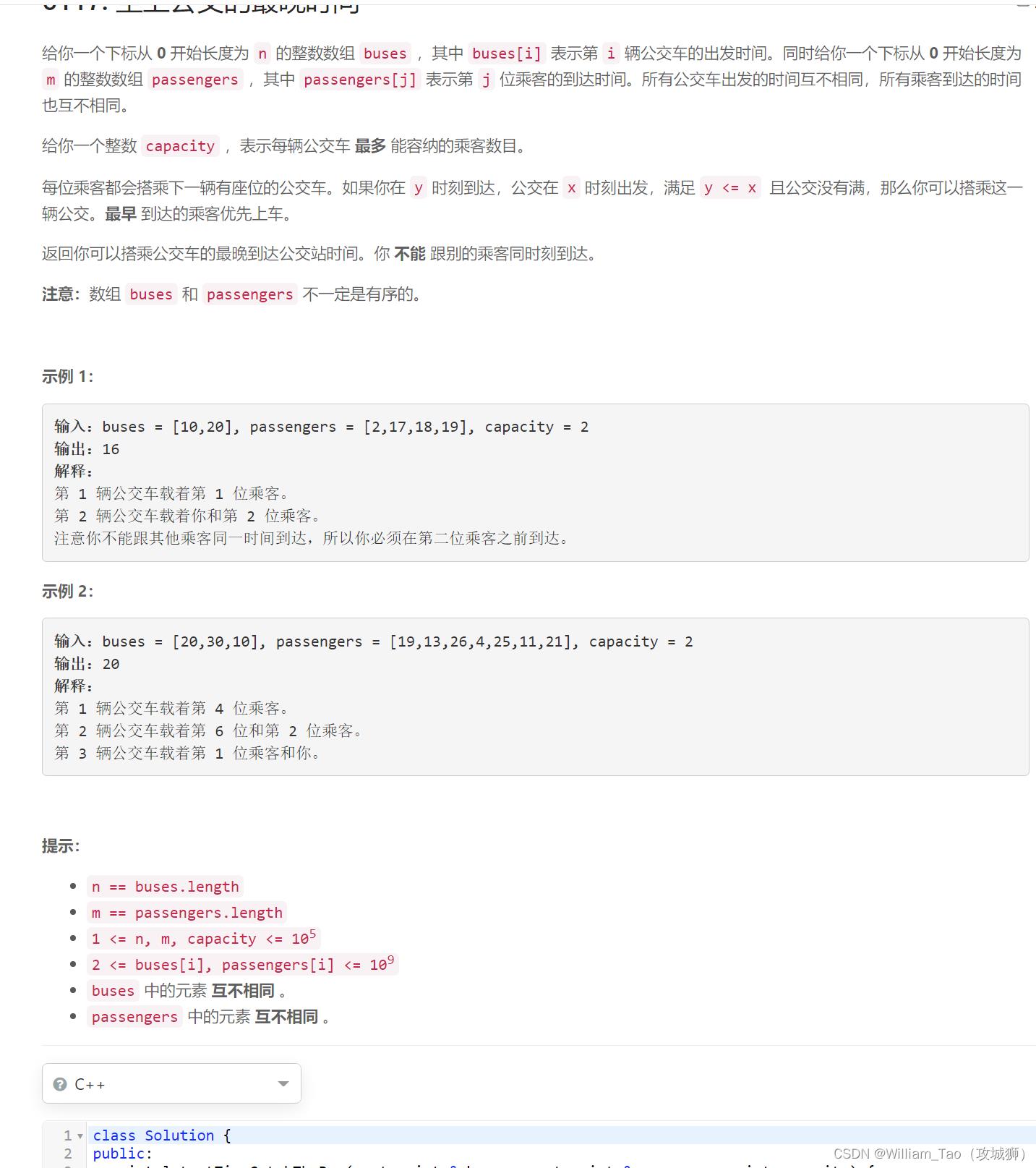
思路:
来源灵佬https://www.bilibili.com/video/BV1Le4y1R7xu/?spm_id_from=333.788&vd_source=11a40407ca73e76119d9f9b789cc7ff2、
排序后,模拟乘客上车的过程。
模拟结束后:
如果最后一班公交还有空位,我们可以在发车时到达公交站,如果此刻有人,我们可以顺着他往前找到没人到达的时刻;
如果最后一班公交没有空位,我们可以找到上一个上车的乘客,顺着他往前找到一个没人到达的时刻。作者:endlesscheng
链接:https://leetcode.cn/problems/the-latest-time-to-catch-a-bus/solution/pai-xu-by-endlesscheng-h9w9/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
class Solution
public:
int latestTimeCatchTheBus(vector<int>& buses, vector<int>& passengers, int capacity)
sort(buses.begin(), buses.end());
sort(passengers.begin(), passengers.end());
//j代表上车的人数,c代表当前的容量剩余
int j=0,c;
for(int t:buses)
//此时容量有剩余且当前的人数未到达全部乘客的人数,乘客来的比公交早
for(c=capacity;c&&j<passengers.size()&&passengers[j]<= t;j++)
c--;
j--;//代表最后一个上车的乘客
//顺着最后一个人往前找,找到即答案
int ans = c ? buses.back() : passengers[j];
while (j >= 0 && passengers[j--] == ans) --ans; // 往前找没人到达的时刻
return ans;
;
6118. 最小差值平方和
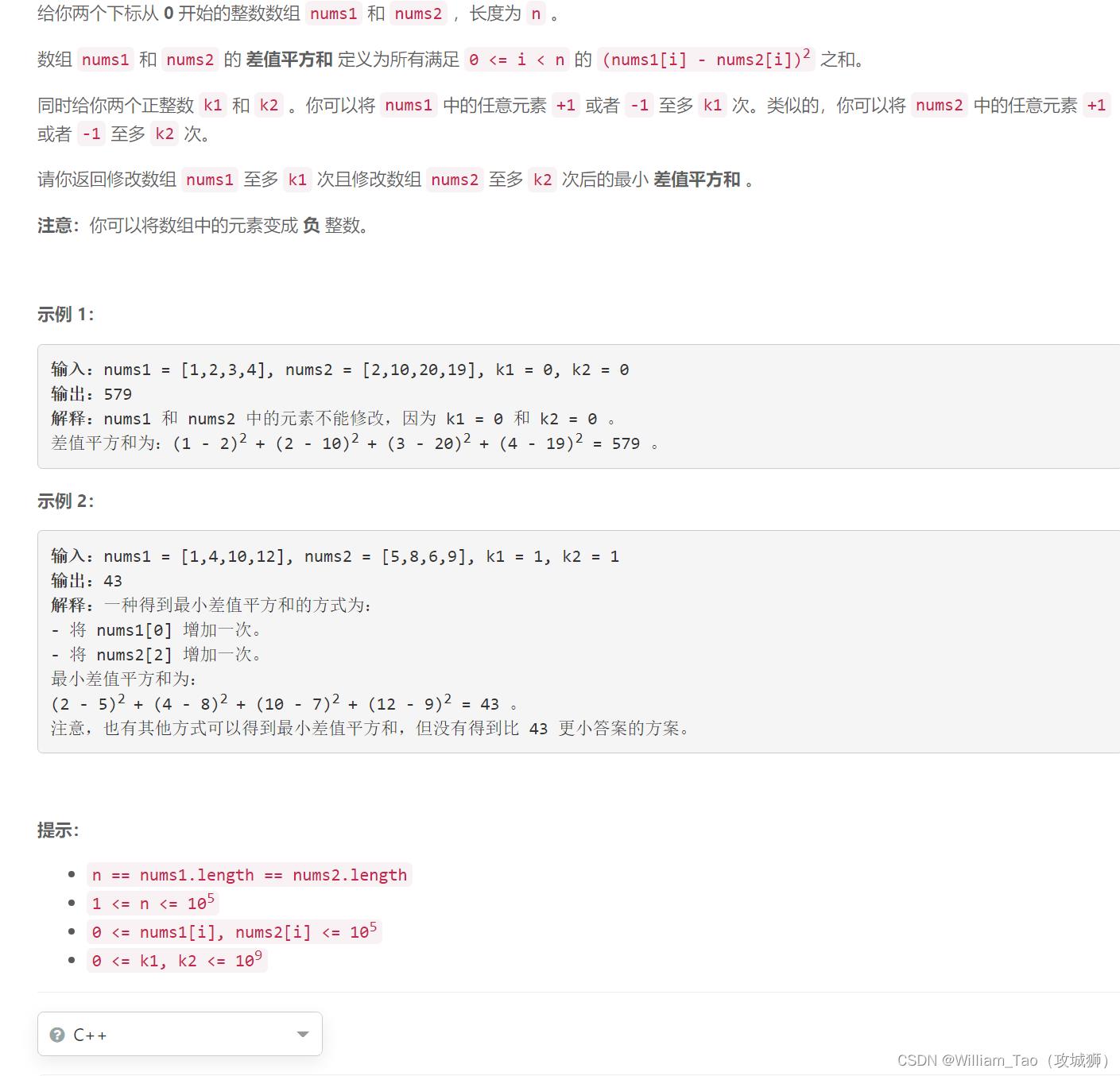
贪心 + 二分查找
参考:
https://leetcode.cn/problems/minimum-sum-of-squared-difference/solution/c-by-lao-hang-n-a2sg/
class Solution
bool check(vector<int> diff, int mid, int cnt)
long long sum = 0; // sum注意要为long long,不然int类型存不下100000*100000
for(int i: diff)
sum += (max(i, mid) - mid);
return sum<=cnt; // 操作数小于k1+k2说明大值都可以缩小到mid
public:
long long minSumSquareDiff(vector<int>& nums1, vector<int>& nums2, int k1, int k2)
int n = nums1.size();
long long sum=0;
vector<int> diff(n);
for(int i=0;i<n;i++)
diff[i]=abs(nums1[i]-nums2[i]);
sum+= diff[i];
if(sum<=k1+k2) return 0;
//二分求目标值
int target, left = 0, right = 100001;
while(left<=right)
int mid = left +(right-left)/2;
if(check(diff,mid,k1+k2))
target = mid;
right=mid-1;
else
left = mid+1;
//
int res=k1+k2;
// 将所有大于target的值变为target
for(int i = 0; i < n; ++i)
if(diff[i]>target)
res-=(diff[i]-target); // 减去将该值变为target所需的操作数
diff[i]=target; // 更新该值为target
// 如果剩余操作数大于0,说明还可以继续操作差值数组
// 继续对大值们进行修改,此时数组中的大值均为target,那么就为target的项就减去1,操作数也减1
for(int i=0;i<n &&res>0;++i)
if(diff[i]==target)
--diff[i];
--res;
long long ans=0;
for(int i:diff)
ans+=1ll*i*i;
return ans;
;
6119 元素值大于变化阈值的子数组

思路:
本题我的思路是,每次给一个子数组的长度,然后再遍历该长度下的子数组中所有元素是否能够全部符合题目条件,如果符合就把当前长度加入到一个set当中,最后遍历set的值即可。(好像不对,题目只要求有一个符合的即可)
别人的思路:
目前弄懂了单调栈的解法,还有并查集的方法目前还没有弄懂
/*
单调栈的应用:
不妨枚举nums[i]并假设某包含nums[i]的子段是长度为k的某段中最小的数字
在该段中其余数字都大于nums[i],只要nums[i]>threshold/k,那么段内的所有元素均大于threshold/k
我们只需要求出有没有这样的nums[i]就可以知道是否有符合题意的k
怎样维护某个nums[i]在某个段内是最小的数字?我们只需要找到nums[i]左边和右边首个严格小于nums[i]的索引
那么索引之间就是nums[i]这段的波及范围
快速求nums[i]左边和右边首个小于nums[i]的元素属于Next Greater问题,可以用单调栈解决
时间复杂度:O(N) 空间复杂度:O(N)
*/
class Solution
public:
int validSubarraySize(vector<int>& nums, int threshold)
int n=nums.size();
stack<int> s;
int left[n];// left[i] 为左侧小于 nums[i] 的最近元素位置(不存在时为 -1)
for(int i=0;i<n;i++)
// 遇到nums[i]<=nums[栈顶索引] -> 弹出栈顶索引直至nums[i]>nums[栈顶索引]
// 此时nums[栈顶索引]就是nums[i]左边首个严格小于nums[i]的数字
// 被弹出的那些栈顶元素是不可能成为后面left[i]有效取值的,因为会优先取到当前的nums[i]
// e.g. nums[st1]=[1,2,4,5] nums[i]=3 显然4与5不符合题意弹出 3才是符合题意的 加入后面有个6进来了
// 必然会优先取到3而不会取更前面的4与5
while(!s.empty() &&nums[s.top()] >=nums[i])
s.pop();
left[i]=s.empty() ?-1:s.top(); // 栈顶的必定1严格小于nums[i]并且是最近的(-1表示取全部)
s.push(i);
int right[n];
s = stack<int>();
for(int i=n-1;i>=0;i--)
while(!s.empty() &&nums[s.top()] >=nums[i])
s.pop();
right[i]=s.empty() ?n:s.top();
s.push(i);
// 枚举nums[i]根据其波及范围确定到k,再判断k是否合法
for(int i=0;i<n;i++)
int k = right[i]-left[i]-1;
// cout<<k;
if(nums[i]>threshold/k)return k;
return -1;
;
总结:
本次LeetCode周赛看了评论,普遍说难度大。对我来说也是,哈哈。很自闭,赛后看解析都很费力。
本次的题目的类型分别为 1.二叉树的应用(还行)2.脑筋急转弯 3.贪心+二分 4.并查集/单调栈
本次需要补的内容有:单调栈的内容,并查集的的内容以及类型的题目。重新回顾一下 3/4两题的解题方法。
在下周的时候重点学习一下相关欠缺的内容,绝不忙不刷题。
以上是关于LeetCode 双周赛 104(2023/05/13)流水的动态规划,铁打的结构化思考的主要内容,如果未能解决你的问题,请参考以下文章