数据结构教程之树

Posted 2023-05-13 eason66

树大家都见过吧

当然，我们今天说的不是这个树，而是这个

这玩意和大自然中的树有啥关系呢

很简单

首先，做一个树的简笔画

然后，在每条树枝的起点和终点画上圆圈，树枝交会的地方也要画

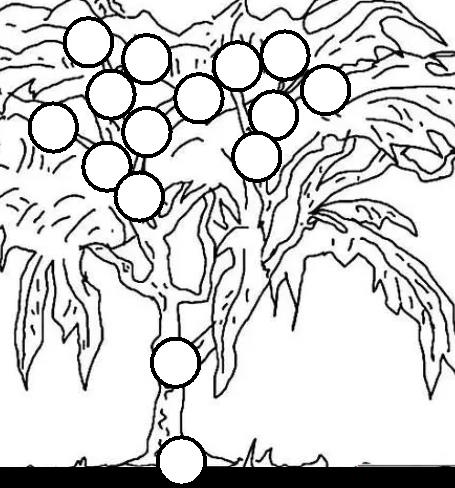
其次，在圆圈间树枝的地方用直线连接

随后，把原来的简笔画去掉，整理一下圆圈，凑得太紧的分开一点，太远的离近一点

最后，上下颠倒一下

好了，画完了

让我们看看维基百科上是怎么定义树的

在计算机科学中，树（英语：tree）是一种抽象数据类型（ADT）或是实现这种抽象数据类型的数据结构，用来模拟具有树状结构性质的数据集合。它是由n（n>0）个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。它具有以下的特点：

• 每个节点都只有有限个子节点或无子节点；
• 没有父节点的节点称为根节点；
• 每一个非根节点有且只有一个父节点；
• 除了根节点外，每个子节点可以分为多个不相交的子树；
• 树里面没有环路(cycle)

是不是看不懂了？

关于树的一些专有名词

1. 树上面的每个圆圈都叫做节点(Node)
2. 每个节点上方或斜上方都有且只有一个节点跟他链接（除了最上面的那个），上面的那个节点叫做这个节点的父节点(Parent)
3. 每个节点下方都有一些节点跟他链接（除了最下方的一堆节点），下面的那些节点叫做这个节点的子节点(child)
4. 同一个节点的子节点叫做兄弟节点或同���节点，简称兄弟或同胞(Sibling)
5. 每个节点上方的所有节点叫做这个节点的祖宗节点或祖先节点，简称祖宗或祖先(Ancestor)
6. 下方的所有节点叫做这个节点的子孙节点或后代节点，简称子孙或后代(Descendant)
7. 树有且只有一个根节点(Root)，在原来树根的位置，也就是树的最上方的节点。根节点没有父节点。
8. 树可以有一至无数个叶子节点(Leaves)，在原来树叶的位置，也就是树最下方的一堆节点。叶子节点没有子节点
9. 一个非叶子节点的节点的子节点的所有子孙节点也可以构成一棵树，叫做这个节点的子树，这个子节点就是该树的根节点。
10. 树中两个节点有且只有一条路可走，这条路被叫做两节点间的路径，这条路径经过的黑线多少就是这条路径的长度，也叫节点间的距离
11. 从根节点到叶子节点的路径中，路径长度最长的那根的长度加一就是该树的深度（因为距离是按黑线算的而深度是按节点数算的）
12. 如果根节点到某些节点的距离相等，那么这些节点在同一层上，这一层的深度就是它到根节点的距离

还看不懂是不是，我们给上图的树编上编号讲解一下
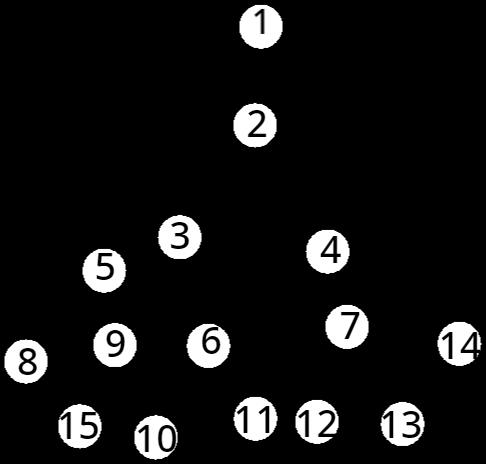[^1]

[^1]注：图中各节点编号是按照层经行编的，即先第一层从左到右，再第二层，第三层……按照这个顺序搜索树的所有节点叫做广度优先搜索，简称广搜(Breadth-First Search,简称BFS)

这棵树的根节点是1号，叶子节点有8、15、10、11、12、13、14七个。
7的子节点最多，有三个，分别为12、13、14。而7的父节点是4号。
去掉1号节点，剩下的节点刚好可以组成一个以2号节点为根节点的树，这棵树就是1号的子树。

这棵树的深度是6，第一层有一个节点：1，第二层是2，第三层有3和4，第四层是5、6、7，第五层是8、9、10、11、12、13、14，其中8、9是兄弟，10、11是兄弟，12、13、14也是兄弟，第六层是15。5、8、9、15是3的子孙，而1、2是3的祖先。

现在基本理解了吧

特殊的树

二叉树

二叉树，顾名思义，就是最多只有两个叉的树。也就是说，每个节点最多只能拥有两个子节点。像之前展示的树就不是二叉树，因为7有三个子节点。删除14后上面的树就是二叉树了。

老规矩，上维基百科

在计算机科学中，二叉树（英语：Binary tree）是每个节点最多只有两个分支（即不存在分支度大于2的节点）的树结构。通常分支被称作“左子树”或“右子树”。二叉树的分支具有左右次序，不能随意颠倒。

因为二叉树最多只有两个子节点，也就是说它每个节点的子节点数只能是0、1、2。因此，我们把二叉树左侧的子节点叫做左孩子(left child)，右侧的叫右孩子(right child)

如果这个节点只有一个子节点，在二叉树中也得分左右。二叉树的左右孩子不能颠倒

如下面的二叉树：

其中，5没有左孩子，9没有右孩子。他们虽然只有一个子节点，但仍然要在子节点上分出左右。很多使用二叉树的地方左子和右子的含义是有区别的，一定不能颠倒！

特殊的二叉树

完全二叉树

完全二叉树指除了倒数第二层以外，其余所有层的节点都有两个子节点，且最下层只有右侧是空的的二叉树，如下图所示：

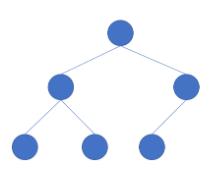
而下图就不是，因为在最下层中间出现了空位。完全二叉树只允许在最右侧出现空位

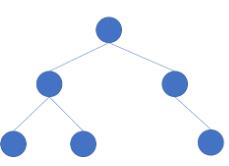
满二叉树（完美二叉树）

顾名思义，满二叉树就是在完全二叉树的基础上，最下层也全是满的的二叉树。也就是说，满二叉树除了最下层的叶子节点外，其余所有节点都有且仅有两个子节点。如下图所示：

满二叉树是一种特殊的完全二叉树！

关于二叉树，我们暂时说到这里。二叉树还有很多更复杂的东西，我们以后会单独出片文章讲解。

森林

森林其实不是树。顾名思义，森林就是很多棵树在一起，如下图所示：

有没有觉得这张图有亿点熟悉？

没错，添加一个2号节点，作为3号和4号的父节点，这个森林就变成一棵树了，就是文章开头的那颗去掉一号。

因此，任何森林都可以添加一个节点作为森林中所有树的父节点，把这个森林转化成一棵树。

森林没太多用处，我们就不多赘述

本期文章到此结束。以后没有球球了，老有人说我这是波兰球，是个P，波兰球哪有个人拟人。由于我这个公众号同时在更新波兰球内容，为了防止给波兰球小白带来误导，以后没有球球了。

数据结构之树（Java 实现版）

实现功能：

　　1.实现了树的构建；

　　2.实现了树的前序递归遍历、后序递归遍历、中序递归遍历；

 1 class BinaryTreeNode{
 2         int data;
 3         BinaryTreeNode leftNode = null, rightNode = null;
 4         
 5         public void setBinaryTreeNode(int data) {
 6             this.data = data;
 7         }
 8         public void setLeftNode(BinaryTreeNode leftNode) {
 9             this.leftNode = leftNode;
10         }
11         public void setRightNode(BinaryTreeNode rightNode) {
12             this.rightNode = rightNode;
13         }
14     }
15 
16 class BinaryTree{
17     BinaryTreeNode[] btn;
18     BinaryTreeNode rooNode;
19     int NodeSize;
20     
21     public BinaryTree(int[] arrayNode) {
22         NodeSize = arrayNode.length;
23         btn = new BinaryTreeNode[NodeSize];
24         
25         //把arrayNode元素转化为节点
26         for(int i = 0; i < NodeSize; i++){
27             btn[i] = new BinaryTreeNode();
28             btn[i].setBinaryTreeNode(arrayNode[i]);
29             if(i == 0){
30                 rooNode = btn[i];
31             }
32         }
33         //把二叉树的左右子树节点补全
34         for(int j = 0; j <= (NodeSize - 2)/2; j++){
35             btn[j].setLeftNode(btn[2*j + 1]);
36             btn[j].setRightNode(btn[2*j + 2]);
37         }
38     }
39     //递归方法前序遍历
40     void preOrder(BinaryTreeNode btn){
41         BinaryTreeNode root = btn;
42         if(root != null){
43             printNode(root);
44             inOrder(root.leftNode);
45             inOrder(root.rightNode);
46         }
47     }
48     //递归方法中序遍历
49     void inOrder(BinaryTreeNode btn){
50         BinaryTreeNode root = btn;
51         
52         if(root != null){
53             inOrder(root.leftNode);
54             printNode(root);
55             inOrder(root.rightNode);
56         }
57     }
58     //递归方法后序遍历
59     void postOrder(BinaryTreeNode btn){
60         BinaryTreeNode root = btn;
61         
62         if(root != null){
63             postOrder(root.leftNode);
64             postOrder(root.rightNode);
65             printNode(root);
66         }
67     }
68     //打印节点信息
69     static void printNode(BinaryTreeNode btn){
70         int a = btn.data;
71         System.out.println(a);
72     }
73 }
74 
75 public class Tree {
76     public static void main(String[] args) {
77         int[] arrayNode = new int[]{1,2,3,4,5,6,7,8,9};
78         BinaryTree bt = new BinaryTree(arrayNode);
79         System.out.println("inOrder:");
80         bt.inOrder(bt.rooNode);
81         System.out.println("preOrder:");
82         bt.preOrder(bt.rooNode);
83         System.out.println("postOrder:");
84         bt.postOrder(bt.rooNode);
85     }
86 }