03 SVM - KKT条件

Posted 2023-05-13

参考技术A

02 SVM - 拉格朗日乘子法

回顾上章，原始问题与对偶问题的关系：

结论：
1、对偶问题小于等于原始问题。
2、当函数满足KKT条件的时候，对偶问题=原始问题。

这章开始介绍KKT条件。

KKT条件是泛拉格朗日乘子法的一种形式；主要应用在当我们的优化函数存在不等值约束的情况下的一种最优化求解方式；KKT条件即满足不等式约束情况下的条件。

回顾 不等式约束的定义：

1、可行解必须在约束区域g(x)之内，由图可知可行解x只能在g(x)<0和g(x)=0的区域取得；
(1) 当可行解x在g(x)<0的区域中的时候，此时直接极小化f(x)即可得到；
(2) 当可行解x在g(x)=0的区域中的时候，此时直接等价于等式约束问题的求解。

2、当可行解在约束内部区域的时候，令β=0即可消去约束。

3、 对于参数β的取值而言，在等值约束中，约束函数和目标函数的梯度只要满足平行即可，而在不等式约束中，若β≠0，则说明可行解在约束区域的边界上，这个时候可行解应该尽可能的靠近无约束情况下的解，所以在约束边界上，目标函数的负梯度方向应该远离约束区域朝无约束区域时的解，此时约束函数的梯度方向与目标函数的负梯度方向应相同；从而可以得出β>0。

1、拉格朗日取得可行解的充要条件；
2、将不等式约束转换后的一个约束，称为松弛互补条件；
3、初始的约束条件；
4、 初始的约束条件；
5.、不等式约束需要满足的条件；

04 SVM - 感知器模型

给大家介绍两款超级牛逼的算法！SVM · SMO算法！和牛逼也很难 !

 

KKT 条件

先来看如何选取参数。在 SMO 算法中，我们是依次选取参数的：

选出违反 KKT 条件最严重的样本点、以其对应的参数作为第一个参数第二个参数的选取有一种比较繁复且高效的方法，但对于一个朴素的实现而言、第二个参数即使随机选取也无不可

 

可以以一张图来直观理解这里提到的诸多概念：

 

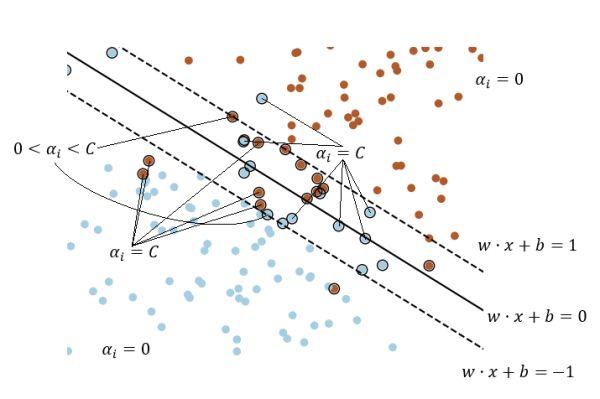
（画得有点乱，见谅……）

图中外面有个黑圆圈的其实就是传说中的“支持向量”，其定义会在文末给出

那么我们到底应该如何刻画“违反 KKT 条件”这么个东西呢？从直观上来说，我们可以有这么一种简单有效的定义：

 

得益于 Numpy 强大的 Fancy Indexing，上述置 0 的实现非常好写（？？？）：

 

至于 SMO 算法的第二步，正如前文所说，它的本质就是一个带约束的二次规划，虽然求解过程可能会比较折腾，但其实难度不大。具体步骤会放在文末，这里就暂时按下

SMO 的效果

仍是先看看螺旋线数据集上的训练过程：

 

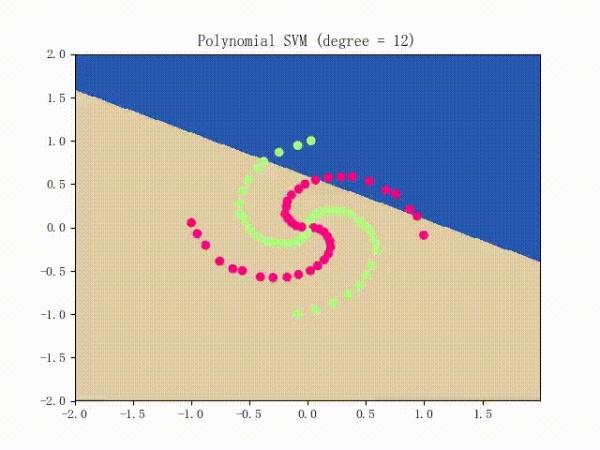
略显纠结，不过还是不错的

接下来看看蘑菇数据集上的表现；单就这个数据集而言，我们实现的朴素 SVM 和 sklearn 中的 SVM 表现几乎是一致的（在使用 RBF 核时），比较具有代表性的训练曲线则如下图所示：

 

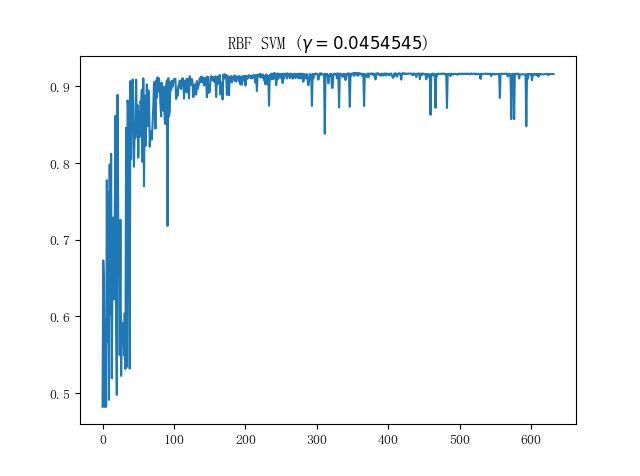
也算是符合 SMO 这种每次只取两个参数进行更新的训练方法的直观

 

（虽然这些在 Python · SVM（二）· LinearSVM 中介绍过，不过为了连贯性，这里还是再介绍一遍）

于是，最优解自然需要满足这么个条件：

 

 

 

 

 

 

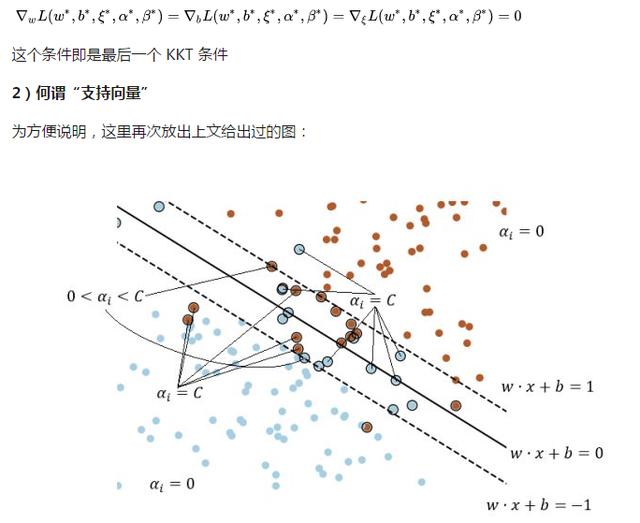
至此，SVM 算法的介绍就大致告一段落了。我们从感知机出发，依次介绍了“极大梯度法”、MBGD（Batch 梯度下降）法、核方法和 SMO 算法；虽然都有点浅尝辄止的味道，但覆盖的东西……大概还是挺多的

希望观众老爷们能够喜欢~

进群：125240963  即可获取数十套PDF哦